MESTRADO PROFISSIONAL EM MATEMÁTICA EM REDE NACIONAL. ENQ Gabarito
|
|
|
- Maria do Carmo Carrilho Peralta
- 6 Há anos
- Visualizações:
Transcrição
1 MESTRADO PROFISSIONAL EM MATEMÁTICA EM REDE NACIONAL ENQ Gabarito Questão 01 [ 1,25 ] Determine as equações das duas retas tangentes à parábola de equação y = x 2 2x + 4 que passam pelo ponto (2, 5). A equação de uma reta tangente à parábola que passa pelo ponto (2, 5) é caracterizada por y = m(x 2) 5, onde m é a inclinação e o sistema seguinte possui solução única, isto é, a interseção da reta com a parábola possui um único ponto. { y = x 2 2x + 4 y = m(x 2) 5 Assim, x 2 2x + 4 = m(x 2) 5, donde x 2 (2 + m)x + 2m + 9 = 0. O sistema terá uma única solução se, e somente se, = b 2 4ac = 0. Calculando = (2 + m) 2 4(2m + 9) = m 2 4m 32, obtemos = 0 se, e somente se, m = 8 ou m = 4. Portanto, y = 8x 21 e y = 4x + 3 são as equações pedidas. Escrever a equação de uma reta passando por (2, 5). [0,25] Caracterizar a reta tangente. [0,25] Concluir que o sistema tem solução única se, e somente se, = 0. [0,25] Determinar as duas equações. [0,5] Questão 02 [ 1,25 ] Descreva a construção, com régua e compasso, do círculo tangente à reta r e contendo os pontos A e B da figura abaixo. Observação: Considere conhecidas as construções, com régua e compasso, da mediatriz de um segmento, da média geométrica de dois segmentos e da perpendicular a um segmento passando por um ponto dado. Estas construções podem ser utilizadas sem maiores detalhamentos.
2 Vamos supor o problema resolvido: Para construir o círculo, precisamos construir, primeiramente, seu centro C. Este centro estará na interseção da mediatriz do segmento AB com a reta perpendicular a r e passando pelo ponto T de tangência entre r e o círculo. Com isso, se soubermos determinar o ponto T, o problema poderá ser facilmente resolvido. Sendo P o ponto de interseção entre r e a reta que passa por A e B, sabemos que P A P B = P T 2, logo, P T é a média geométrica dos segmentos P A e P B. Com isso, podemos fazer a seguinte construção: 1. Marcamos o ponto P de interseção entre as retas da figura e construímos o círculo de centro P e raio a, onde a é a média geométrica dos segmentos P A e P B (esta construção pode, segundo o enunciado, ser feita sem maiores detalhes). 2. Tomamos o ponto T na interseção entre r e o círculo do passo anterior, de forma que T P A seja agudo. 3. Traçamos a reta s, perpendicular a r e passando por T (segundo o enunciado, esta construção pode ser feita sem maiores detalhes). 4. Traçamos a reta m, mediatriz de AB (esta construção pode ser feita sem maiores detalhes). 5. Marcamos o centro C do círculo na interseção entre m e s. 6. Construímos o círculo de centro C e raio CA. Indicar (mesmo que apenas em uma figura) que o centro do círculo está na mediatriz de AB e na reta perpendicular a r passando por T, ou seguir claramente uma estratégia que utiliza este fato. [0,25] Considerar a média geométrica entre os segmentos P A e P B. [0,25] Tomar o ponto T de forma que P T seja a média geométrica entre os segmentos P A e P B. [0,5] Finalizar a construção do círculo, tomando o centro na mediatriz de AB e na perpendicular a r passando por T. [0,25] Questão 03 [ 1,25 ::: (a)=0,50; (b)=0,75 ] (a) Prove que um número inteiro positivo n possui uma quantidade ímpar de divisores positivos se, e somente se, é um quadrado perfeito. (b) Sejam a e b números inteiros positivos com (a, b) = 1. Prove que, se ab é um quadrado perfeito, então a e b são quadrados perfeitos.
3 (a) Pelo teorema fundamental da aritmética, n = p α 1 1 p α 2 2 pα k k sendo p 1 < p 2 < < p k números primos e α 1, α 2,..., α k números inteiros positivos. A quantidade de divisores de n é dado por d(n) = (α 1 + 1) (α 2 + 1) (α k + 1). (i) Se n tem um número ímpar de divisores, então todos os fatores de d(n) são números ímpares, ou seja, α 1, α 2,, α k são números pares. Portanto ( α 1 α 2 n = p 2 1 p 2 2 p (ii) Por outro lado, se n é um quadrado perfeito, então n = c 2 para algum c Z. Isto implica que todos os α i são números pares e então d(n) é ímpar, por ser o produto de ímpares. (b) Sejam a = a β 1 1 aβ 2 2 aβs s e b = b γ 1 1 bγ 2 2 bγ t t a decomposição destes números em fatores primos distintos. O fato de (a, b) = 1 implica que a e b não tem fator primo comum. Portanto a decomposição de ab em fatores primos é α k 2 k ) 2. ab = a β 1 1 a β 2 2 a βs s b γ 1 1 b γ 2 2 b γ t t Como ab é um quadrado perfeito, pelo item (a) a quantidade de divisores de ab é um número ímpar, isto é, d(ab) = (β 1 + 1) (β 2 + 1) (β s + 1) (γ 1 + 1) (γ 2 + 1) (γ t + 1) é ímpar. Logo d(a) é ímpar, d(b) é ímpar e novamente pelo item (a) os números a e b são quadrados perfeitos. Item (a) Supor que n tem uma quantidade ímpar de divisores e concluir que n é quadrado perfeito. [0,25] Supor que n é quadrado perfeito e concluir que n tem uma quantidade ímpar de divisores. [0,25] Escrever corretamente a decomposição em primos de ab, usando o fato (a, b) = 1. [0,25] Concluir que a e b são quadrados perfeitos. [0,5] alternativa para o item (b): (b) Sejam a = a β 1 1 aβ 2 2 aβs s e b = b γ 1 1 bγ 2 2 bγ t t a decomposição destes números em fatores primos distintos. O fato de (a, b) = 1 implica que a e b não tem fator primo comum. Portanto a decomposição de ab em fatores primos é ab = a β 1 1 a β 2 2 a βs s b γ 1 1 b γ 2 2 b γ t t. Como ab é um quadrado perfeito, os expoentes β i e γ j são todos pares. Logo as decomposições de a = a β 1 1 aβ 2 2 aβs s e b = b γ 1 1 bγ 2 2 bγ t t em fatores primos distintos têm expoentes pares. Portanto os números a e b são quadrados perfeitos. Escrever corretamente a decomposição de ab em primos distintos usando o fato de que (a, b) = 1. [0,25] Concluiur que a e b são quadrados perfeitos. [0,50]
4 Questão 04 [ 1,25 ::: (a)=0,50; (b)=0,75 ] Uma permutação de n elementos é dita caótica quando nenhum elemento está na posição original. Por exemplo, (2, 1, 4, 5, 3) e (3, 4, 5, 2, 1) são permutações caóticas de (1, 2, 3, 4, 5), mas (3, 2, 4, 5, 1) não é, pois 2 está no lugar original. O número de permutações caóticas de n elementos é denotado por D n. (a) Determine D 4 listando todas as permutações caóticas de (1, 2, 3, 4). (b) Quantas são as permutações de (1, 2, 3, 4, 5, 6, 7) que têm exatamente três números em suas posições original? (a) As permutações caóticas de (1, 2, 3, 4) são 2143, 2341, 2413, 3142, 3412, 3421, 4123, 4312 e (b) Primeiro escolhemos 3 números entre 1 e 7 que ficam na posição original, o que pode ser feito de C 3 7 Devemos fazer uma permutação caótica com as demais 4 posições, e isso pode ser feito de D 4 = 9 maneiras. = 35 maneiras. Portanto temos um total de C 3 7 D 4 = 315 permutações de (1, 2, 3, 4, 5, 6, 7) que têm exatamente três números em suas posições originais. (a) Listar as 9 permutações caóticas de (1, 2, 3, 4). [0,5] Não listar todas as permutações caóticas de (1, 2, 3, 4) mas listar pelo menos 6, sendo todas as listadas caóticas. [0,25] (b) Concluir que existem 35 modos de escolher os 3 números que ficarão na posição original. [0,25] Concluir que cada escolha dos 3 números fixados na posição original gera D 4 permutações caóticas. [0,25] Concluir a contagem 35 D 4. [0, 25] Questão 05 [ 1,25 ::: (a)=0,50; (b)=0,75 ] Um tetraedro ABCD possui como base o triângulo equilátero BCD, cujos lados têm medida 1. Suas faces laterais são tais que AB = AC = AD = l, com BÂC = CÂD = BÂD = α. (a) Expresse l em função de α. (b) Determine, em função de α, a medida da altura deste tetraedro traçada a partir de A.
5 (a) Considerando a face ABC, como l = AB = AC e BC = 1, temos, pela Lei do Cossenos, 1 2 = l 2 + l 2 2 l l cos α, que implica logo Com isso, 2l 2 (1 cos α) = 1, l 2 = 1 2(1 cos α). 1 l = 2(1 cos α). (b) Como as faces ABC, ACD e ABD são triângulos isósceles de vértice A, as alturas relativas a A de cada uma dessas faces têm seus pés nos pontos médios de BC, CD e BD, respectivamente. Da mesma forma, as alturas da face BCD, que é um triângulo equilátero, têm pés nos mesmos pontos médios, como mostra a figura abaixo. Assim, as projeções das arestas AB, AC e AD sobre a base estão sobre as alturas da base, de forma que H, pé da altura AH do tetraedro, esteja então no incentro/ortocentro/baricentro do triângulo equilátero BCD. Como a altura do triângulo BCD tem medida 3 2, temos Assim, como AHB é retângulo em H, temos BH = CH = DH = 2 3 AH 2 + BH 2 = AB 2, = 3. logo que nos dá Com isso, que é a altura pedida AH 2 + ( ) 2 3 = l 2, 3 AH = 1 2(1 cos α). 1 AH = 2(1 cos α) 1 3, Item (a): Aplicar a lei dos cossenos. [0,25]
6 Obter l em função de α. [0,25] : Obter a distância 3/3 entre um dos vértices da base (B, C ou D) e o pé H da altura pedida. [0,25] Considerar um dos triângulos retângulos ABH, ACH ou ADH. [0,25] Encontrar a altura correta. [0,25] Questão 06 [ 1,25 ::: (a)=0,50; (b)=0,75 ] (a) Prove a relação de Stifel: para todos n e p inteiros positivos com n p, (b) Considere a sequência de números inteiros a 1 = C2, 2 Mostre que a n = C 3 n+2. C p+1 n+1 = Cp+1 n + C p n. a n = C Cn+1, 2 n 2. (a) Se n = p obtemos 1 = Suponhamos então n > p. Temos que Cn p+1 + Cn p n! = (p + 1)!(n p 1)! + n! n!(n p) + n!(p + 1) = p!(n p)! (p + 1)!(n p)!) Cn p+1 + Cn p n!(n + 1) = (p + 1)!(n p)! = (n + 1)! (p + 1)!(n p)! = Cp+1 n+1 (b) Para n = 2 temos a 2 = C C 2 3 = = C 3 4, portanto a afirmação é verdadeira. Suponhamos a n = C 3 n+2, para n fixo, n 2. Vamos provar que o resultado vale para n + 1, isto é, a n+1 = C 3 n+3. Temos que a n+1 = a n + C 2 n+2 = C 3 n+2 + C 2 n+2 (hipótese de indução). Agora, usando a relação de Stifel, obtemos a n+1 = C 3 n+2 + C 2 n+2 = C 3 n+3 Portanto, pelo princípio de indução, o resultado é válido para todo n 2. Item (a) Provar a relação de Stifel. [0,5] Verificar o resultado para n = 2 (base da indução). [0,25] Supor o resultado válido para n e provar para n + 1. [0,5] alternativa para o item (a) com argumento combinatório:
7 (a) Suponha que de um grupo de n + 1 pessoas tenham que ser formada uma comissão com p + 1 pessoas. Por definição de número binomial segue que o lado esquerdo da igualdade é uma solução possível para o problema. Por outro lado, fixemos uma pessoa, digamos P. Vamos considerar as comissões que contém P e as comissões que não contém P. O número de elementos do primeiro conjunto é igual a y = C p n, pois como P já faz parte, resta escolher p entre as demais n. Já, o número de comissões sem P é igual a x = Cn p+1. Portanto segue o resultado. Temos então que x + y = C p+1 n+1. Item (a) Encontrar x e y. [0,25] Concluir que C p+1 n+1 = x + y. [0,25] alternativa para o item (b): (b) Pela relação de Stifel temos C 3 4 = C C 2 3 C 3 5 = C C 2 4 C6 3 = C5 3 + C5 2. C 3 n+1 = C 3 n + C 2 n C 3 n+2 = C 3 n+1 + C 2 n+1. Somando-se as igualdades acima, membro a membro, obtemos que C 3 n+2 = C C C 2 n + C 2 n+1. Como C 3 3 = C 2 2 = 1 segue que C 3 n+2 = C C C 2 n + C 2 n+1. Listar todas as igualdade de Stifel de 4 e n + 2. [0,25] Somar termo a termo e concluir a igualdade. [0,50]
8 Questão 07 [ 1,25 ::: (a)=0,75; (b)=0,50 ] Uma função f é dita crescente em X R se, para todos x 1, x 2 X com x 1 < x 2, tem-se f(x 1 ) < f(x 2 ). Sabendo que as funções g(x) = x a e h(x) = b x são crescentes em [0, + ) para a e b reais com a > 0 e b > 1, (a) prove que a função F (x) = (1 + e x ) x2 +1 é crescente em [0, + ); (b) encontre as soluções não negativas da equação (1 + e x ) x2 +1 = 2. (a) Suponha x 1 < x 2, onde x 1, x 2 [0, ). Como as funções g(x) = x a e h(x) = b x são crescentes em [0, + ) para a e b reais com a > 0 e b > 1, tem-se que x 1 < x 2 = x a 1 < x a 2 e b x 1 < b x 2 Assim, x 2 1 < x 2 2 (tomamos a = 2) e daí x < x Concluimos, tomando b = 1 + e x 1 > 1, que (1 + e x 1 ) x < (1 + e x 1 ) x (1) Por outro lado, tomando b = e > 1, tem-se que e x 1 < e x 2, logo e x 1 +1 < e x Agora, tomando a = x , concluimos que (1 + e x 1 ) x < (1 + e x 2 ) x (2) Usando as desigualdades (1) e (2) concluimos, pela transitividade, que F (x 1) = (1 + e x 1 ) x < F (x 2) = (1 + e x 2 ) x Portanto, a função F é crescente. (b) Temos que a função F (x) = (1 + e x ) x2 +1 é crescente, consequentemente é injetora. A equação (1 + e x ) x2 +1 = 2 é equivalente à F (x) = 2 = F (0). Portanto, x = 0 é a única solução não negativa. (a) Concluir a desigualdade (1). [0,25] Concluir a desigualdade (2). [0,25] Concluir que a função é crescente. [0,25] (b) Concluir que a função é injetiva. [0,25] Achar a solução única. [0,25]
9 Questão 08 [ 1,25 ::: (a)=0,50; (b)=0,75 ] (a) Sejam a, b, m números inteiros, com m > 1 e tais que (a, m) = 1. Prove que a congruência ax 1 mod m possui solução. Além disso, mostre que se x 1, x 2 Z são soluções da congruência, então x 1 x 2 mod m. (b) Resolva a congruência 13x 1 mod (a) Suponha (a, m) = 1. Segue que existem inteiros r, s tais que a r + m s = 1. Daí temos que ar 1 mod m, portanto r é solução. Suponha agora que x 1, x 2 são soluções, isto é, ax 1 1 mod m e ax 2 1 mod m. Segue que, ax 1 ax 2 mod m, Como (a, m) = 1, concluimos que x 1 x 2 mod m. (b) Considere a congruência 13 x 1 mod Calculando o mdc(2436, 13) obtemos Portanto, mdc(2436, 13) = 1. Agora, usando o algoritmo euclidiano estendido, obtemos ( 5) = 1 Portanto, x 937 mod Item (a) Mostrar que a congruência tem solução. [0,25] Mostrar que duas soluções são congruentes módulo m. [0,25] Mostrar 13 e 2436 são primos entre si. [0,25] Achar a solução geral. [0,5] Achar apenas uma solução particular. [0,25]
MESTRADO PROFISSIONAL EM MATEMÁTICA EM REDE NACIONAL. ENQ Gabarito. a(x x 0) = b(y 0 y).
 MESTRADO PROFISSIONAL EM MATEMÁTICA EM REDE NACIONAL ENQ 016.1 Gabarito Questão 01 [ 1,00 ::: (a)=0,50; (b)=0,50 ] (a) Seja x 0, y 0 uma solução da equação diofantina ax + by = c, onde a, b são inteiros
MESTRADO PROFISSIONAL EM MATEMÁTICA EM REDE NACIONAL ENQ 016.1 Gabarito Questão 01 [ 1,00 ::: (a)=0,50; (b)=0,50 ] (a) Seja x 0, y 0 uma solução da equação diofantina ax + by = c, onde a, b são inteiros
ENQ Gabarito MESTRADO PROFISSIONAL EM MATEMÁTICA EM REDE NACIONAL. Questão 01 [ 1,25 ]
![ENQ Gabarito MESTRADO PROFISSIONAL EM MATEMÁTICA EM REDE NACIONAL. Questão 01 [ 1,25 ] ENQ Gabarito MESTRADO PROFISSIONAL EM MATEMÁTICA EM REDE NACIONAL. Questão 01 [ 1,25 ]](/thumbs/67/56480825.jpg) MESTRADO PROFISSIONAL EM MATEMÁTICA EM REDE NACIONAL ENQ 017 Gabarito Questão 01 [ 1,5 ] Encontre as medidas dos lados e ângulos de dois triângulos ABC diferentes tais que AC = 1, BC = e A BC = 0 Considere
MESTRADO PROFISSIONAL EM MATEMÁTICA EM REDE NACIONAL ENQ 017 Gabarito Questão 01 [ 1,5 ] Encontre as medidas dos lados e ângulos de dois triângulos ABC diferentes tais que AC = 1, BC = e A BC = 0 Considere
Material Teórico - Módulo: Vetores em R 2 e R 3. Módulo e Produto Escalar - Parte 2. Terceiro Ano - Médio
 Material Teórico - Módulo: Vetores em R 2 e R 3 Módulo e Produto Escalar - Parte 2 Terceiro Ano - Médio Autor: Prof. Angelo Papa Neto Revisor: Prof. Antonio Caminha M. Neto Nesta segunda parte, veremos
Material Teórico - Módulo: Vetores em R 2 e R 3 Módulo e Produto Escalar - Parte 2 Terceiro Ano - Médio Autor: Prof. Angelo Papa Neto Revisor: Prof. Antonio Caminha M. Neto Nesta segunda parte, veremos
MESTRADO PROFISSIONAL EM MATEMÁTICA EM REDE NACIONAL. ENQ Gabarito
 MESTRADO PROFISSIONAL EM MATEMÁTICA EM REDE NACIONAL ENQ 016. Gabarito Questão 01 [ 1,00 ] A secretaria de educação de um município recebeu uma certa quantidade de livros para distribuir entre as escolas
MESTRADO PROFISSIONAL EM MATEMÁTICA EM REDE NACIONAL ENQ 016. Gabarito Questão 01 [ 1,00 ] A secretaria de educação de um município recebeu uma certa quantidade de livros para distribuir entre as escolas
MESTRADO PROFISSIONAL EM MATEMÁTICA EM REDE NACIONAL. ENQ Gabarito
 MESTRADO PROFISSIONAL EM MATEMÁTICA EM REDE NACIONAL ENQ 2018.1 Gabarito Questão 01 [ 1,25 ::: (a)=0,50; (b)=0,75 ] Isótopos radioativos de um elemento químico estão sujeitos a um processo de decaimento
MESTRADO PROFISSIONAL EM MATEMÁTICA EM REDE NACIONAL ENQ 2018.1 Gabarito Questão 01 [ 1,25 ::: (a)=0,50; (b)=0,75 ] Isótopos radioativos de um elemento químico estão sujeitos a um processo de decaimento
ENQ Gabarito MESTRADO PROFISSIONAL EM MATEMÁTICA EM REDE NACIONAL. (a) Sejam a, b, n Z com n > 0. Mostre que a + b a 2n b 2n.
 MESTRADO PROFISSIONAL EM MATEMÁTICA EM REDE NACIONAL ENQ 2018.2 Gabarito Questão 01 [ 1,25 ::: (a)=0,50; (b)=0,75 ] (a) Sejam a, b, n Z com n > 0. Mostre que a + b a 2n b 2n. (b) Para quais valores de
MESTRADO PROFISSIONAL EM MATEMÁTICA EM REDE NACIONAL ENQ 2018.2 Gabarito Questão 01 [ 1,25 ::: (a)=0,50; (b)=0,75 ] (a) Sejam a, b, n Z com n > 0. Mostre que a + b a 2n b 2n. (b) Para quais valores de
MESTRADO PROFISSIONAL EM MATEMÁTICA EM REDE NACIONAL. ENQ Gabarito
 MESTRADO PROFISSIONAL EM MATEMÁTICA EM REDE NACIONAL ENQ 20152 Gabarito Questão 01 [ 1,00 ::: (a)0,50; (b)0,50 ] Determine TODOS os valores possíveis para os algarismos x, y, z e t de modo que os números
MESTRADO PROFISSIONAL EM MATEMÁTICA EM REDE NACIONAL ENQ 20152 Gabarito Questão 01 [ 1,00 ::: (a)0,50; (b)0,50 ] Determine TODOS os valores possíveis para os algarismos x, y, z e t de modo que os números
MESTRADO PROFISSIONAL EM MATEMÁTICA EM REDE NACIONAL. ENQ Gabarito. c1 + c 2 = 1 c 1 + 4c 2 = 3. a n = n. c 1 = 1 2c 1 + 2c
 MESTRADO PROFISSIONAL EM MATEMÁTICA EM REDE NACIONAL ENQ 2019.1 Gabarito Questão 01 [ 1,25 ::: (a)=0,50; (b)=0,75 ] Resolva as seguintes recorrências: (a) a n+2 5a n+1 + 4a n = 0, a 0 = 1, a 1 = 3. (b)
MESTRADO PROFISSIONAL EM MATEMÁTICA EM REDE NACIONAL ENQ 2019.1 Gabarito Questão 01 [ 1,25 ::: (a)=0,50; (b)=0,75 ] Resolva as seguintes recorrências: (a) a n+2 5a n+1 + 4a n = 0, a 0 = 1, a 1 = 3. (b)
IME º DIA MATEMÁTICA BERNOULLI COLÉGIO E PRÉ-VESTIBULAR
 IME - 2004 1º DIA MATEMÁTICA BERNOULLI COLÉGIO E PRÉ-VESTIBULAR Matemática Questão 01 CALCULE o número natural n que torna o determinante a seguir igual a 5. Por Chio, tem-se Matemática Questão 02 Considere
IME - 2004 1º DIA MATEMÁTICA BERNOULLI COLÉGIO E PRÉ-VESTIBULAR Matemática Questão 01 CALCULE o número natural n que torna o determinante a seguir igual a 5. Por Chio, tem-se Matemática Questão 02 Considere
GABARITO E PAUTA DE CORREÇÃO DO ENQ Questão 2 [ 1,0 pt ::: (a)=0,5; (b)=0,5 ] Sejam a, b, p inteiros, com p primo.
![GABARITO E PAUTA DE CORREÇÃO DO ENQ Questão 2 [ 1,0 pt ::: (a)=0,5; (b)=0,5 ] Sejam a, b, p inteiros, com p primo. GABARITO E PAUTA DE CORREÇÃO DO ENQ Questão 2 [ 1,0 pt ::: (a)=0,5; (b)=0,5 ] Sejam a, b, p inteiros, com p primo.](/thumbs/70/62605338.jpg) GABARITO E PAUTA DE CORREÇÃO DO ENQ-014. Questão 1 [ 1,0 pt ::: (a)=0,5; (b)=0,5 ] Sejam a, b, p inteiros, com p primo. Demonstre que: (a) se p não divide a, então (p, a) = 1. (b) se p ab, então p a ou
GABARITO E PAUTA DE CORREÇÃO DO ENQ-014. Questão 1 [ 1,0 pt ::: (a)=0,5; (b)=0,5 ] Sejam a, b, p inteiros, com p primo. Demonstre que: (a) se p não divide a, então (p, a) = 1. (b) se p ab, então p a ou
Lista 5. Geometria, Coleção Profmat, SBM. Problemas selecionados da seção 4.1, pág. 147 em diante.
 MA13 Exercícios das Unidades 8, 9 e 10 2014 Lista 5 Geometria, Coleção Profmat, SBM. Problemas selecionados da seção 4.1, pág. 147 em diante. 1) As retas r, s e t são paralelas com s entre r e t. As transversais
MA13 Exercícios das Unidades 8, 9 e 10 2014 Lista 5 Geometria, Coleção Profmat, SBM. Problemas selecionados da seção 4.1, pág. 147 em diante. 1) As retas r, s e t são paralelas com s entre r e t. As transversais
AVF - MA Gabarito
 MESTRADO PROFISSIONAL EM MATEMÁTICA EM REDE NACIONAL AVF - MA13-016.1 - Gabarito Questão 01 [,00 pts ] Em um triângulo ABC de perímetro 9, o lado BC mede 3 e a distância entre os pés das bissetrizes interna
MESTRADO PROFISSIONAL EM MATEMÁTICA EM REDE NACIONAL AVF - MA13-016.1 - Gabarito Questão 01 [,00 pts ] Em um triângulo ABC de perímetro 9, o lado BC mede 3 e a distância entre os pés das bissetrizes interna
ENQ Gabarito e Pauta de Correção
 ENQ014.1 - Gabarito e Pauta de Correção Questão 1 [ 1,0 pt ] O máximo divisor comum de dois inteiros positivos é 0. Para se chegar a esse resultado pelo processo das divisões sucessivas, os quocientes
ENQ014.1 - Gabarito e Pauta de Correção Questão 1 [ 1,0 pt ] O máximo divisor comum de dois inteiros positivos é 0. Para se chegar a esse resultado pelo processo das divisões sucessivas, os quocientes
Lista 11. Geometria, Coleção Profmat, SBM. Problemas selecionados das seções 7.2 (pág. 311) e 7.3 (pág. 329).
 MA13 Exercícios das Unidades 17 e 18 2014 Lista 11 Geometria, Coleção Profmat, SBM. Problemas selecionados das seções 7.2 (pág. 311) e 7.3 (pág. 329). 1) Sejam dados um ponto A e um plano α com A α. Prove
MA13 Exercícios das Unidades 17 e 18 2014 Lista 11 Geometria, Coleção Profmat, SBM. Problemas selecionados das seções 7.2 (pág. 311) e 7.3 (pág. 329). 1) Sejam dados um ponto A e um plano α com A α. Prove
XXVI Olimpíada Brasileira de Matemática GABARITO Segunda Fase
 XXVI Olimpíada Brasileira de Matemática GABARITO Segunda Fase Soluções Nível Solução do Problema : Os possíveis produtos x k x k são ( )( ) =, ( + )( + ) = + e ( )( + ) =. Suponha que a produtos são iguais
XXVI Olimpíada Brasileira de Matemática GABARITO Segunda Fase Soluções Nível Solução do Problema : Os possíveis produtos x k x k são ( )( ) =, ( + )( + ) = + e ( )( + ) =. Suponha que a produtos são iguais
CM127 - Lista Mostre que os pontos médios de um triângulo isósceles formam um triângulo também isósceles.
 CM127 - Lista 2 Congruência de Triângulos e Desigualdade Triangular 1. Faça todos os exercícios dados em aula. 2. Em um triângulo ABC a altura do vértice A é perpendicular ao lado BC e divide BC em dois
CM127 - Lista 2 Congruência de Triângulos e Desigualdade Triangular 1. Faça todos os exercícios dados em aula. 2. Em um triângulo ABC a altura do vértice A é perpendicular ao lado BC e divide BC em dois
Na forma reduzida, temos: (r) y = 3x + 1 (s) y = ax + b. a) a = 3, b, b R. b) a = 3 e b = 1. c) a = 3 e b 1. d) a 3
 01 Na forma reduzida, temos: (r) y = 3x + 1 (s) y = ax + b a) a = 3, b, b R b) a = 3 e b = 1 c) a = 3 e b 1 d) a 3 1 0 y = 3x + 1 m = 3 A equação que apresenta uma reta com o mesmo coeficiente angular
01 Na forma reduzida, temos: (r) y = 3x + 1 (s) y = ax + b a) a = 3, b, b R b) a = 3 e b = 1 c) a = 3 e b 1 d) a 3 1 0 y = 3x + 1 m = 3 A equação que apresenta uma reta com o mesmo coeficiente angular
1. A partir da definição, determinar a equação da parábola P, cujo foco é F = (3, 4) e cuja diretriz é L : x + y 2 = 0. (x 3) 2 + (y + 4) 2 =
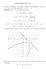 QUESTÕES-AULA 18 1. A partir da definição, determinar a equação da parábola P, cujo foco é F = (3, 4) e cuja diretriz é L : x + y = 0. Solução Seja P = (x, y) R. Temos que P P d(p, F ) = d(p, L) (x 3)
QUESTÕES-AULA 18 1. A partir da definição, determinar a equação da parábola P, cujo foco é F = (3, 4) e cuja diretriz é L : x + y = 0. Solução Seja P = (x, y) R. Temos que P P d(p, F ) = d(p, L) (x 3)
CONCURSO DE ADMISSÃO AO COLÉGIO MILITAR DO RECIFE - 99 / 00 PROVA DE CIÊNCIAS EXATAS DA. 1 a é equivalente a a
 13 1 a PARTE - MATEMÁTICA MÚLTIPLA ESCOLHA ESCOLHA A ÚNICA RESPOSTA CERTA, ASSINALANDO-A COM X NOS PARÊNTESES À ESQUERDA Item 01. Se a R e a 0, a expressão: 1 a é equivalente a a a.( ) 1 b.( ) c.( ) a
13 1 a PARTE - MATEMÁTICA MÚLTIPLA ESCOLHA ESCOLHA A ÚNICA RESPOSTA CERTA, ASSINALANDO-A COM X NOS PARÊNTESES À ESQUERDA Item 01. Se a R e a 0, a expressão: 1 a é equivalente a a a.( ) 1 b.( ) c.( ) a
Aula 7 Complementos. Exercício 1: Em um plano, por um ponto, existe e é única a reta perpendicular
 MODULO 1 - AULA 7 Aula 7 Complementos Apresentamos esta aula em forma de Exercícios Resolvidos, mas são resultados importantes que foram omitidos na primeira aula que tratou de Conceitos Básicos. Exercício
MODULO 1 - AULA 7 Aula 7 Complementos Apresentamos esta aula em forma de Exercícios Resolvidos, mas são resultados importantes que foram omitidos na primeira aula que tratou de Conceitos Básicos. Exercício
Gabarito e Pauta de Correção ENQ
 Gabarito e Pauta de Correção ENQ 015.1 Questão 01 [ 1,00 ::: (a=0,50; (b=0,50 ] (a Mostre que se x e y são números irracionais tais que x y seja racional não nulo, então x + y e x y são ambos irracionais.
Gabarito e Pauta de Correção ENQ 015.1 Questão 01 [ 1,00 ::: (a=0,50; (b=0,50 ] (a Mostre que se x e y são números irracionais tais que x y seja racional não nulo, então x + y e x y são ambos irracionais.
10. Determine as equações cartesianas das famílias de retas que fazem um ângulo de π/4 radianos com a reta y = 2x + 1.
 Geometria Analítica. 1. Determine as posições relativas e as interseções entre os conjuntos em R abaixo. Em cada item também faça um esboço dos dois conjuntos dados no mesmo sistema de eixos. (a) C : (x
Geometria Analítica. 1. Determine as posições relativas e as interseções entre os conjuntos em R abaixo. Em cada item também faça um esboço dos dois conjuntos dados no mesmo sistema de eixos. (a) C : (x
Teorema de Tales. MA13 - Unidade 8. Resumo elaborado por Eduardo Wagner baseado no texto: A. Caminha M. Neto. Geometria.
 Teorema de Tales MA13 - Unidade 8 Resumo elaborado por Eduardo Wagner baseado no texto: A. Caminha M. Neto. Geometria. Coleção PROFMAT Proporcionalidade 1. Dizemos que o segmento x é a quarta proporcional
Teorema de Tales MA13 - Unidade 8 Resumo elaborado por Eduardo Wagner baseado no texto: A. Caminha M. Neto. Geometria. Coleção PROFMAT Proporcionalidade 1. Dizemos que o segmento x é a quarta proporcional
Colégio Naval 2008/2009 (PROVA VERDE)
 Colégio Naval 008/009 (PROVA VERDE) 01) Um triângulo retângulo, de lados expressos por números inteiros consecutivos, está inscrito em um triângulo eqüilátero T de lado x. Se o maior cateto é paralelo
Colégio Naval 008/009 (PROVA VERDE) 01) Um triângulo retângulo, de lados expressos por números inteiros consecutivos, está inscrito em um triângulo eqüilátero T de lado x. Se o maior cateto é paralelo
MA13 Geometria AVF 2014
 MA1 Geometria AVF 014 Questão 1 [,0 pt ] Na figura, AB AC e a bissetriz interna traçada de B intersecta o lado AC em P de forma que AP + BP = BC. Os pontos Q e D são tomados de forma que BQ BP e P D é
MA1 Geometria AVF 014 Questão 1 [,0 pt ] Na figura, AB AC e a bissetriz interna traçada de B intersecta o lado AC em P de forma que AP + BP = BC. Os pontos Q e D são tomados de forma que BQ BP e P D é
1. Quantos são os planos determinados por 4 pontos não coplanares?justifique.
 Universidade Federal de Uberlândia Faculdade de Matemática Disciplina: Geometria euclidiana espacial (GMA010) Assunto: Paralelisno e Perpendicularismo; Distância e Ângulos no Espaço. Prof. Sato 1 a Lista
Universidade Federal de Uberlândia Faculdade de Matemática Disciplina: Geometria euclidiana espacial (GMA010) Assunto: Paralelisno e Perpendicularismo; Distância e Ângulos no Espaço. Prof. Sato 1 a Lista
UNIVERSIDADE FEDERAL DE VIÇOSA DEPARTAMENTO DE MATEMÁTICA LISTA DE EXERCÍCIOS DE MAT243-CÁLCULO III
 UNIVERSIDADE FEDERAL DE VIÇOSA DEPARTAMENTO DE MATEMÁTICA LISTA DE EXERCÍCIOS DE MAT243-CÁLCULO III Capítulo 1 Vetores no Rn 1. Sejam u e v vetores tais que e u v = 2 e v = 1. Calcule v u v. 2. Sejam u
UNIVERSIDADE FEDERAL DE VIÇOSA DEPARTAMENTO DE MATEMÁTICA LISTA DE EXERCÍCIOS DE MAT243-CÁLCULO III Capítulo 1 Vetores no Rn 1. Sejam u e v vetores tais que e u v = 2 e v = 1. Calcule v u v. 2. Sejam u
Geometria Analítica I
 Geom. Analítica I Respostas do Módulo I - Aula 14 1 Geometria Analítica I 10/03/011 Respostas dos Exercícios do Módulo I - Aula 14 Aula 14 1. a. A equação do círculo de centro h, k) e raio r é x h) + y
Geom. Analítica I Respostas do Módulo I - Aula 14 1 Geometria Analítica I 10/03/011 Respostas dos Exercícios do Módulo I - Aula 14 Aula 14 1. a. A equação do círculo de centro h, k) e raio r é x h) + y
BANCO DE EXERCÍCIOS - 24 HORAS
 BANCO DE EXERCÍCIOS - 24 HORAS 9º ANO ESPECIALIZADO/CURSO ESCOLAS TÉCNICAS E MILITARES FOLHA Nº 13 EXERCÍCIOS 1) A representação cartesiana da função y = ax 2 + bx + c é a parábola abaixo. Tendo em vista
BANCO DE EXERCÍCIOS - 24 HORAS 9º ANO ESPECIALIZADO/CURSO ESCOLAS TÉCNICAS E MILITARES FOLHA Nº 13 EXERCÍCIOS 1) A representação cartesiana da função y = ax 2 + bx + c é a parábola abaixo. Tendo em vista
NOTAÇÕES. R N C i z. ]a, b[ = {x R : a < x < b} (f g)(x) = f(g(x)) n. = a 0 + a 1 + a a n, sendo n inteiro não negativo.
![NOTAÇÕES. R N C i z. ]a, b[ = {x R : a < x < b} (f g)(x) = f(g(x)) n. = a 0 + a 1 + a a n, sendo n inteiro não negativo. NOTAÇÕES. R N C i z. ]a, b[ = {x R : a < x < b} (f g)(x) = f(g(x)) n. = a 0 + a 1 + a a n, sendo n inteiro não negativo.](/thumbs/74/70891793.jpg) R N C i z det A d(a, B) d(p, r) AB Â NOTAÇÕES : conjunto dos números reais : conjunto dos números naturais : conjunto dos números complexos : unidade imaginária: i = 1 : módulo do número z C : determinante
R N C i z det A d(a, B) d(p, r) AB Â NOTAÇÕES : conjunto dos números reais : conjunto dos números naturais : conjunto dos números complexos : unidade imaginária: i = 1 : módulo do número z C : determinante
Teorema do ângulo externo e sua consequencias
 Teorema do ângulo externo e sua consequencias Definição. Os ângulos internos de um triângulo são os ângulos formados pelos lados do triângulo. Um ângulo suplementar a um ângulo interno do triângulo é denominado
Teorema do ângulo externo e sua consequencias Definição. Os ângulos internos de um triângulo são os ângulos formados pelos lados do triângulo. Um ângulo suplementar a um ângulo interno do triângulo é denominado
Seja AB = BC = CA = 4a. Sendo D o ponto de interseção da reta s com o lado AC temos, pelo teorema de Tales, AD = 3a e DC = a.
 GABARITO MA1 Geometria I - Avaliação 2-201/2 Questão 1. (pontuação: 2) As retas r, s e t são paralelas, como mostra a figura abaixo. A distância entre r e s é igual a e a distância entre s e t é igual
GABARITO MA1 Geometria I - Avaliação 2-201/2 Questão 1. (pontuação: 2) As retas r, s e t são paralelas, como mostra a figura abaixo. A distância entre r e s é igual a e a distância entre s e t é igual
A equação da circunferência
 A UA UL LA A equação da circunferência Introdução Nas duas últimas aulas você estudou a equação da reta. Nesta aula, veremos que uma circunferência desenhada no plano cartesiano também pode ser representada
A UA UL LA A equação da circunferência Introdução Nas duas últimas aulas você estudou a equação da reta. Nesta aula, veremos que uma circunferência desenhada no plano cartesiano também pode ser representada
Aula 1. Exercício 1: Exercício 2:
 Aula 1 Exercício 1: Com centro em A e raio de medida m achamos dois pontos B e C na reta, esses dois pontos são os centros das circunferências pedidas (2 soluções ). Exercício 2: Com centro em B e raio
Aula 1 Exercício 1: Com centro em A e raio de medida m achamos dois pontos B e C na reta, esses dois pontos são os centros das circunferências pedidas (2 soluções ). Exercício 2: Com centro em B e raio
LISTA DE EXERCÍCIOS MAT GEOMETRIA E DESENHO GEOMÉTRICO I
 LISTA DE EXERCÍCIOS MAT 230 - GEOMETRIA E DESENHO GEOMÉTRICO I 1. Numa geometria de incidência, o plano tem 5 pontos. Quantas retas tem este plano? A resposta é única? 2. Exibir um plano de incidência
LISTA DE EXERCÍCIOS MAT 230 - GEOMETRIA E DESENHO GEOMÉTRICO I 1. Numa geometria de incidência, o plano tem 5 pontos. Quantas retas tem este plano? A resposta é única? 2. Exibir um plano de incidência
Objetivos. em termos de produtos internos de vetores.
 Aula 5 Produto interno - Aplicações MÓDULO 1 - AULA 5 Objetivos Calcular áreas de paralelogramos e triângulos. Calcular a distância de um ponto a uma reta e entre duas retas. Determinar as bissetrizes
Aula 5 Produto interno - Aplicações MÓDULO 1 - AULA 5 Objetivos Calcular áreas de paralelogramos e triângulos. Calcular a distância de um ponto a uma reta e entre duas retas. Determinar as bissetrizes
1. Área do triângulo
 UNIVERSIDADE DO ESTADO DE MATO GROSSO CAMPUS UNIVERSITÁRIO DE SINOP FACULDADE DE CIÊNCIAS EXATAS E TECNOLÓGICAS CURSO DE ENGENHARIA CIVIL DISCIPLINA: FUNDAMENTOS DE MATEMÁTICA Geometria Plana II Prof.:
UNIVERSIDADE DO ESTADO DE MATO GROSSO CAMPUS UNIVERSITÁRIO DE SINOP FACULDADE DE CIÊNCIAS EXATAS E TECNOLÓGICAS CURSO DE ENGENHARIA CIVIL DISCIPLINA: FUNDAMENTOS DE MATEMÁTICA Geometria Plana II Prof.:
Módulo Elementos Básicos de Geometria Plana - Parte 2. Congruência de Triângulos e Aplicações. Professores Cleber Assis e Tiago Miranda
 Módulo Elementos Básicos de Geometria Plana - Parte 2 Congruência de Triângulos e Aplicações. 8 ano E.F. Professores Cleber Assis e Tiago Miranda Elementos Básicos de Geometria Plana - Parte 2. Congruência
Módulo Elementos Básicos de Geometria Plana - Parte 2 Congruência de Triângulos e Aplicações. 8 ano E.F. Professores Cleber Assis e Tiago Miranda Elementos Básicos de Geometria Plana - Parte 2. Congruência
tg30 = = 2 + x 3 3x = x 3 3 Tem-se que AB C = 90, AD B = 90 e DA B = 60 implicam em DB C = 60. Assim, do triângulo retângulo BCD, vem
 Resposta da questão : [C] 5 senα α 0 0 7,05 senβ 0,705 α 45 0 Portanto, AO B 0 + 45 75. Resposta da questão : [B] x x Tem-se que sen0 x 5 m. 0 0 Portanto, a resposta é 0 00% 00%. 5 Resposta da questão
Resposta da questão : [C] 5 senα α 0 0 7,05 senβ 0,705 α 45 0 Portanto, AO B 0 + 45 75. Resposta da questão : [B] x x Tem-se que sen0 x 5 m. 0 0 Portanto, a resposta é 0 00% 00%. 5 Resposta da questão
EXERCICIOS DE APROFUNDAMENTO - MATEMÁTICA - RETA
 EXERCICIOS DE APROFUNDAMENTO - MATEMÁTICA - RETA - 015 1. (Unicamp 015) Seja r a reta de equação cartesiana x y 4. Para cada número real t tal que 0 t 4, considere o triângulo T de vértices em (0, 0),
EXERCICIOS DE APROFUNDAMENTO - MATEMÁTICA - RETA - 015 1. (Unicamp 015) Seja r a reta de equação cartesiana x y 4. Para cada número real t tal que 0 t 4, considere o triângulo T de vértices em (0, 0),
CM127 - Lista 3. Axioma da Paralelas e Quadriláteros Notáveis. 1. Faça todos os exercícios dados em aula.
 CM127 - Lista 3 Axioma da Paralelas e Quadriláteros Notáveis 1. Faça todos os exercícios dados em aula. 2. Determine as medidas x e y dos ângulos dos triângulos nos itens abaixo 3. Dizemos que um triângulo
CM127 - Lista 3 Axioma da Paralelas e Quadriláteros Notáveis 1. Faça todos os exercícios dados em aula. 2. Determine as medidas x e y dos ângulos dos triângulos nos itens abaixo 3. Dizemos que um triângulo
Concluimos dai que o centro da circunferência é C = (6, 4) e o raio é
 QUESTÕES-AULA 17 1. A equação x 2 + y 2 12x + 8y + 0 = 0 representa uma circunferência de centro C = (a, b) e de raio R. Determinar o valor de a + b + R. Solução Completamos quadrados na expressão dada.
QUESTÕES-AULA 17 1. A equação x 2 + y 2 12x + 8y + 0 = 0 representa uma circunferência de centro C = (a, b) e de raio R. Determinar o valor de a + b + R. Solução Completamos quadrados na expressão dada.
Soluções do Capítulo 8 (Volume 2)
 Soluções do Capítulo 8 (Volume 2) 1. Não. Basta considerar duas retas concorrentes s e t em um plano perpendicular a uma reta r. As retas s e t são ambas ortogonais a r, mas não são paralelas entre si.
Soluções do Capítulo 8 (Volume 2) 1. Não. Basta considerar duas retas concorrentes s e t em um plano perpendicular a uma reta r. As retas s e t são ambas ortogonais a r, mas não são paralelas entre si.
r O GABARITO - QUALIFICAÇÃO - Março de 2013
 GABARITO - QUALIFICAÇÃO - Março de 013 Questão 1. (pontuação: 1,5) É dado um retângulo ABCD tal que em seu interior estão duas circunferências tangentes exteriormente no ponto T, como mostra a figura abaixo.
GABARITO - QUALIFICAÇÃO - Março de 013 Questão 1. (pontuação: 1,5) É dado um retângulo ABCD tal que em seu interior estão duas circunferências tangentes exteriormente no ponto T, como mostra a figura abaixo.
EXERCÍCIOS RESOLVIDOS Prova de 23/07/2009 Todas as questões se referem a um sistema ortogonal de coordenadas
 EXERCÍCIOS RESOLVIDOS 1 SINUÊ DAYAN BARBERO LODOVICI Resumo Exercícios Resolvidos - Geometria Analítica BC 0404 1 Prova de 23/07/2009 Todas as questões se referem a um sistema ortogonal de coordenadas
EXERCÍCIOS RESOLVIDOS 1 SINUÊ DAYAN BARBERO LODOVICI Resumo Exercícios Resolvidos - Geometria Analítica BC 0404 1 Prova de 23/07/2009 Todas as questões se referem a um sistema ortogonal de coordenadas
J. Delgado - K. Frensel - L. Crissaff Geometria Analítica e Cálculo Vetorial
 178 Capítulo 10 Equação da reta e do plano no espaço 1. Equações paramétricas da reta no espaço Sejam A e B dois pontos distintos no espaço e seja r a reta que os contém. Então, P r existe t R tal que
178 Capítulo 10 Equação da reta e do plano no espaço 1. Equações paramétricas da reta no espaço Sejam A e B dois pontos distintos no espaço e seja r a reta que os contém. Então, P r existe t R tal que
UNIVERSIDADE FEDERAL DE VIÇOSA CENTRO DE CIÊNCIAS EXATAS E TECNOLÓGICAS DEPARTAMENTO DE MATEMÁTICA
 1 UNIVERSIDADE FEDERAL DE VIÇOSA CENTRO DE CIÊNCIAS EXATAS E TECNOLÓGICAS DEPARTAMENTO DE MATEMÁTICA 1 a Lista de exercícios MAT 41 - Cálculo III - 01/II Coordenadas no espaço 1. Determinar o lugar geométrico
1 UNIVERSIDADE FEDERAL DE VIÇOSA CENTRO DE CIÊNCIAS EXATAS E TECNOLÓGICAS DEPARTAMENTO DE MATEMÁTICA 1 a Lista de exercícios MAT 41 - Cálculo III - 01/II Coordenadas no espaço 1. Determinar o lugar geométrico
TIPO-A. Matemática. 03. Considere os números naturais a = 25, b = 2, c = 3, d = 4 e analise as afirmações seguintes:
 2 Matemática 01. Recorde que uma função f: R R diz-se par quando f( x) = f(x) para todo x real, e que f diz-se ímpar quando f( x) = f(x) para todo x real. Com base nessas definições, analise a veracidade
2 Matemática 01. Recorde que uma função f: R R diz-se par quando f( x) = f(x) para todo x real, e que f diz-se ímpar quando f( x) = f(x) para todo x real. Com base nessas definições, analise a veracidade
GABARITO Prova Verde. GABARITO Prova Rosa
 Sistema ELITE de Ensino COLÉGIO NAVAL 011/01 GABARITO Prova Verde MATEMÁTICA 01 E 11 D 0 D 1 A 03 E 13 ANULADA 0 E 1 ANULADA 05 D 15 B 06 D 16 C 07 B 17 C 08 E 18 B 09 A 19 A 10 C-Passível de anulação
Sistema ELITE de Ensino COLÉGIO NAVAL 011/01 GABARITO Prova Verde MATEMÁTICA 01 E 11 D 0 D 1 A 03 E 13 ANULADA 0 E 1 ANULADA 05 D 15 B 06 D 16 C 07 B 17 C 08 E 18 B 09 A 19 A 10 C-Passível de anulação
XXXVIII Olimpíada Cearense de Matemática Nível 2 - Oitavo e Nono Anos
 XXXVIII Olimpíada Cearense de Matemática Nível 2 - Oitavo e Nono Anos Problema 1. Antônio e Bruno compraram ingressos para um evento. Ao chegarem em casa, eles perceberam que os ingressos eram numerados
XXXVIII Olimpíada Cearense de Matemática Nível 2 - Oitavo e Nono Anos Problema 1. Antônio e Bruno compraram ingressos para um evento. Ao chegarem em casa, eles perceberam que os ingressos eram numerados
Prova final de MATEMÁTICA - 3o ciclo Época especial
 Prova final de MATEMÁTICA - 3o ciclo 017 - Época especial Proposta de resolução Caderno 1 1. Como 3π 9,7 então vem que 9, < 3π < 9,3, pelo que, de entre as opções apresentadas, o número 9,3 é a única aproximação
Prova final de MATEMÁTICA - 3o ciclo 017 - Época especial Proposta de resolução Caderno 1 1. Como 3π 9,7 então vem que 9, < 3π < 9,3, pelo que, de entre as opções apresentadas, o número 9,3 é a única aproximação
Posição relativa entre retas e círculos e distâncias
 4 Posição relativa entre retas e círculos e distâncias Sumário 4.1 Distância de um ponto a uma reta.......... 2 4.2 Posição relativa de uma reta e um círculo no plano 4 4.3 Distância entre duas retas no
4 Posição relativa entre retas e círculos e distâncias Sumário 4.1 Distância de um ponto a uma reta.......... 2 4.2 Posição relativa de uma reta e um círculo no plano 4 4.3 Distância entre duas retas no
Ângulos entre retas Retas e Planos Perpendiculares. Walcy Santos
 Ângulos entre retas Retas e Planos Perpendiculares Walcy Santos Ângulo entre duas retas A idéia do ângulo entre duas retas será adaptado do conceito que temos na Geometria Plana. Se duas retas são concorrentes
Ângulos entre retas Retas e Planos Perpendiculares Walcy Santos Ângulo entre duas retas A idéia do ângulo entre duas retas será adaptado do conceito que temos na Geometria Plana. Se duas retas são concorrentes
Elementos de Matemática Finita
 Elementos de Matemática Finita Exercícios Resolvidos - Princípio de Indução; Algoritmo de Euclides 1. Seja ( n) k n! k!(n k)! o coeficiente binomial, para n k 0. Por convenção, assumimos que, para outros
Elementos de Matemática Finita Exercícios Resolvidos - Princípio de Indução; Algoritmo de Euclides 1. Seja ( n) k n! k!(n k)! o coeficiente binomial, para n k 0. Por convenção, assumimos que, para outros
Olimpíada Mineira de Matemática 2008
 Questão 1) Alternativa C) Olimpíada Mineira de Matemática 008 Resolução Nível III Refletindo a imagem Após 1 hora e 0 minutos Refletindo novamente Observação: A posição original do relógio não é uma configuração
Questão 1) Alternativa C) Olimpíada Mineira de Matemática 008 Resolução Nível III Refletindo a imagem Após 1 hora e 0 minutos Refletindo novamente Observação: A posição original do relógio não é uma configuração
PROMILITARES 08/08/2018 MATEMÁTICA. Professor Rodrigo Menezes
 MATEMÁTICA Professor Rodrigo Menezes Colégio Naval 2012/2013 QUESTÃO 1 Sejam P = 1 + 1 3 1 + 1 5 1 + 1 7 1 + 1 9 1 + 1 11 e Q = 1 1 5 1 1 7 1 1 9 1 1 11 Qual é o valor de P Q? a) 2 b) 2 c) 5 d) 3 e) 5
MATEMÁTICA Professor Rodrigo Menezes Colégio Naval 2012/2013 QUESTÃO 1 Sejam P = 1 + 1 3 1 + 1 5 1 + 1 7 1 + 1 9 1 + 1 11 e Q = 1 1 5 1 1 7 1 1 9 1 1 11 Qual é o valor de P Q? a) 2 b) 2 c) 5 d) 3 e) 5
IME º DIA MATEMÁTICA BERNOULLI COLÉGIO E PRÉ-VESTIBULAR
 IME - 2006 1º DIA MATEMÁTICA BERNOULLI COLÉGIO E PRÉ-VESTIBULAR Matemática Questão 01 Sejam a 1 = 1 i, a n = r + si e a n+1 = (r s) + (r + s)i (n > 1) termos de uma sequência. DETERMINE, em função de n,
IME - 2006 1º DIA MATEMÁTICA BERNOULLI COLÉGIO E PRÉ-VESTIBULAR Matemática Questão 01 Sejam a 1 = 1 i, a n = r + si e a n+1 = (r s) + (r + s)i (n > 1) termos de uma sequência. DETERMINE, em função de n,
XXXI Olimpíada Brasileira de Matemática GABARITO Segunda Fase
 XXXI Olimpíada Brasileira de Matemática GABARITO Segunda Fase Soluções Nível 3 Segunda Fase Parte A CRITÉRIO DE CORREÇÃO: PARTE A Na parte A serão atribuídos 4 pontos para cada resposta correta e a pontuação
XXXI Olimpíada Brasileira de Matemática GABARITO Segunda Fase Soluções Nível 3 Segunda Fase Parte A CRITÉRIO DE CORREÇÃO: PARTE A Na parte A serão atribuídos 4 pontos para cada resposta correta e a pontuação
XX OLIMPÍADA REGIONAL DE MATEMÁTICA DE SANTA CATARINA Resolução do treinamento 6 Nível 3
 UNIVERSIDADE FEDERAL DE SANTA CATARINA CENTRO DE CIÊNCIAS FÍSICAS E MATEMÁTICAS DEPARTAMENTO DE MATEMÁTICA PET MATEMÁTICA XX OLIMPÍADA REGIONAL DE MATEMÁTICA DE SANTA CATARINA Resolução do treinamento
UNIVERSIDADE FEDERAL DE SANTA CATARINA CENTRO DE CIÊNCIAS FÍSICAS E MATEMÁTICAS DEPARTAMENTO DE MATEMÁTICA PET MATEMÁTICA XX OLIMPÍADA REGIONAL DE MATEMÁTICA DE SANTA CATARINA Resolução do treinamento
Expressões Algébricas
 META: Resolver geometricamente problemas algébricos. AULA 11 OBJETIVOS: Introduzir a 4 a proporcional. Construir segmentos que resolvem uma equação algébrica. PRÉ-REQUISITOS O aluno deverá ter compreendido
META: Resolver geometricamente problemas algébricos. AULA 11 OBJETIVOS: Introduzir a 4 a proporcional. Construir segmentos que resolvem uma equação algébrica. PRÉ-REQUISITOS O aluno deverá ter compreendido
Sólidos Geométricos, Poliedros e Volume Prof. Lhaylla Crissaff
 Sólidos Geométricos, Poliedros e Volume 2017.1 Prof. Lhaylla Crissaff www.professores.uff.br/lhaylla Sólidos Geométricos Prisma Pirâmide Cilindro Cone Esfera Prisma Ex.: P é um pentágono. Prisma Prisma
Sólidos Geométricos, Poliedros e Volume 2017.1 Prof. Lhaylla Crissaff www.professores.uff.br/lhaylla Sólidos Geométricos Prisma Pirâmide Cilindro Cone Esfera Prisma Ex.: P é um pentágono. Prisma Prisma
GAAL: Exercícios 1, umas soluções
 GAAL: Exercícios 1, umas soluções 1. Determine o ponto C tal que AC = 2 AB, sendo A = (0, 2), B = (1, 0). R: Queremos C tal que AC = 2 AB. Temos AB = (1 0, 0 ( 2)) = (1, 2), logo 2 AB = (2, 4). Então queremos
GAAL: Exercícios 1, umas soluções 1. Determine o ponto C tal que AC = 2 AB, sendo A = (0, 2), B = (1, 0). R: Queremos C tal que AC = 2 AB. Temos AB = (1 0, 0 ( 2)) = (1, 2), logo 2 AB = (2, 4). Então queremos
Soluções Comentadas Matemática Curso Mentor Colégio Naval. Barbosa, L.S.
 Soluções Comentadas Matemática Curso Mentor Colégio Naval Barbosa, L.S. leonardosantos.inf@gmail.com 30 de dezembro de 2013 2 Sumário I Provas 5 1 Matemática 2013/2014 7 II Soluções 11 2 Matemática 2013/2014
Soluções Comentadas Matemática Curso Mentor Colégio Naval Barbosa, L.S. leonardosantos.inf@gmail.com 30 de dezembro de 2013 2 Sumário I Provas 5 1 Matemática 2013/2014 7 II Soluções 11 2 Matemática 2013/2014
x = 4 2sen30 0 = 4 2(1/2) = 2 2 e y = 4 2 cos 30 0 = 4 2( 3/2) = 2 6.
 CURSO DE PRÉ CÁLCULO ONLINE - PET MATEMÁTICA / UFMG LISTA DE EXERCÍCIOS RESOLVIDOS: Exercício 1 Calcule o valor de x e y indicados na figura abaixo. Solução: No triângulo retângulo ABD, temos que AD mede
CURSO DE PRÉ CÁLCULO ONLINE - PET MATEMÁTICA / UFMG LISTA DE EXERCÍCIOS RESOLVIDOS: Exercício 1 Calcule o valor de x e y indicados na figura abaixo. Solução: No triângulo retângulo ABD, temos que AD mede
BANCO DE EXERCÍCIOS - 24 HORAS
 BANCO DE EXERCÍCIOS - 4 HORAS 9º ANO ESPECIALIZADO/CURSO ESCOLAS TÉCNICAS E MILITARES FOLHA Nº 06 GABARITO COMENTADO 1) De acordo com o texto, 10 alunos gostam de geometria mas não gostam de álgebra, logo
BANCO DE EXERCÍCIOS - 4 HORAS 9º ANO ESPECIALIZADO/CURSO ESCOLAS TÉCNICAS E MILITARES FOLHA Nº 06 GABARITO COMENTADO 1) De acordo com o texto, 10 alunos gostam de geometria mas não gostam de álgebra, logo
Aula 4 Produto Interno
 MÓDULO 1 - AULA 4 Objetivos Aula 4 Produto Interno Definir as noções de ângulo entre dois vetores, a norma de um vetor e a operação de produto interno. Compreender as propriedades básicas da norma e do
MÓDULO 1 - AULA 4 Objetivos Aula 4 Produto Interno Definir as noções de ângulo entre dois vetores, a norma de um vetor e a operação de produto interno. Compreender as propriedades básicas da norma e do
54 CAPÍTULO 2. GEOMETRIA ANALÍTICA ( ) =
 54 CAPÍTULO. GEOMETRIA ANALÍTICA.5 Cônicas O grá co da equação + + + + + = 0 (.4) onde,,,, e são constantes com, e, não todos nulos, é uma cônica. A equação (.4) é chamada de equação geral do grau em e
54 CAPÍTULO. GEOMETRIA ANALÍTICA.5 Cônicas O grá co da equação + + + + + = 0 (.4) onde,,,, e são constantes com, e, não todos nulos, é uma cônica. A equação (.4) é chamada de equação geral do grau em e
Mat. Mat. 2. Luanna Ramos. Monitor: Roberta Teixeira
 Mat. Professor: Alex Amaral Luanna Ramos Monitor: Roberta Teixeira Triângulos: Cevianas e pontos notáveis 07/09 mar RESUMO Ceviana é qualquer segmento que parte de um vértice de um triângulo e corta o
Mat. Professor: Alex Amaral Luanna Ramos Monitor: Roberta Teixeira Triângulos: Cevianas e pontos notáveis 07/09 mar RESUMO Ceviana é qualquer segmento que parte de um vértice de um triângulo e corta o
6.1 equações canônicas de círculos e esferas
 6 C Í R C U LO S E E S F E R A S 6.1 equações canônicas de círculos e esferas Um círculo é o conjunto de pontos no plano que estão a uma certa distância r de um ponto dado (a, b). Desta forma temos que
6 C Í R C U LO S E E S F E R A S 6.1 equações canônicas de círculos e esferas Um círculo é o conjunto de pontos no plano que estão a uma certa distância r de um ponto dado (a, b). Desta forma temos que
BANCO DE EXERCÍCIOS - 24 HORAS
 BANCO DE EXERCÍCIOS - HORAS 9º ANO ESPECIALIZADO/CURSO ESCOLAS TÉCNICAS E MILITARES FOLHA Nº GABARITO COMENTADO ) A função será y,5x +, onde y (preço a ser pago) está em função de x (número de quilômetros
BANCO DE EXERCÍCIOS - HORAS 9º ANO ESPECIALIZADO/CURSO ESCOLAS TÉCNICAS E MILITARES FOLHA Nº GABARITO COMENTADO ) A função será y,5x +, onde y (preço a ser pago) está em função de x (número de quilômetros
J. Delgado - K. Frensel - L. Crissaff Geometria Analítica e Cálculo Vetorial
 76 Capítulo 4 Distâncias no plano e regiões no plano 1. Distância de um ponto a uma reta Dados um ponto P e uma reta r no plano, já sabemos calcular a distância de P a cada ponto P r. Definição 1 Definimos
76 Capítulo 4 Distâncias no plano e regiões no plano 1. Distância de um ponto a uma reta Dados um ponto P e uma reta r no plano, já sabemos calcular a distância de P a cada ponto P r. Definição 1 Definimos
( ) ( ) ( ) ( ) ( ) ( )
 XXX Olimpíada Brasileira de Matemática GABARITO Segunda Fase Soluções Nível Segunda Fase Parte A PARTE A Na parte A serão atribuídos pontos para cada resposta correta e a pontuação máxima para essa parte
XXX Olimpíada Brasileira de Matemática GABARITO Segunda Fase Soluções Nível Segunda Fase Parte A PARTE A Na parte A serão atribuídos pontos para cada resposta correta e a pontuação máxima para essa parte
3º trimestre SALA DE ESTUDOS Data: 11/17 Ensino Médio 3º ano A, B e C. Prof. Maurício Nome: nº
 º trimestre SALA DE ESTUDOS Data: 11/17 Ensino Médio º ano A, B e C. Prof. Maurício Nome: nº CONTEÚDOS: EQUAÇÃO DA RETA E EQUAÇÃO DA CIRCUNFERÊNCIA. 1. (Eear 017) O triângulo ABC a) escaleno b) isósceles
º trimestre SALA DE ESTUDOS Data: 11/17 Ensino Médio º ano A, B e C. Prof. Maurício Nome: nº CONTEÚDOS: EQUAÇÃO DA RETA E EQUAÇÃO DA CIRCUNFERÊNCIA. 1. (Eear 017) O triângulo ABC a) escaleno b) isósceles
BANCO DE EXERCÍCIOS - 24 HORAS
 BANCO DE EXERCÍCIOS - 4 HORAS 9º ANO ESPECIALIZADO/CURSO ESCOLAS TÉCNICAS E MILITARES 1) ( + b)³ = 0 + 5b + 7b² + b³ 8 + 1b + 6b² + b³ = 5b + 7b² + b³ b² 7b 8 = 0 (b 7). (b 1) = 0. Como b é base, b = 7.
BANCO DE EXERCÍCIOS - 4 HORAS 9º ANO ESPECIALIZADO/CURSO ESCOLAS TÉCNICAS E MILITARES 1) ( + b)³ = 0 + 5b + 7b² + b³ 8 + 1b + 6b² + b³ = 5b + 7b² + b³ b² 7b 8 = 0 (b 7). (b 1) = 0. Como b é base, b = 7.
GABARITO COMENTÁRIO PROVA DE MATEMÁTICA (IV SIMULADO ITA/2007) QUESTÕES OBJETIVAS 3 ( 2) ( 2) = 3. 5 m. 64 x
 D: 00 08 º EM MATEMÁTICA ITA IME SIMUL COMENT Rosângela o Ensino Médio PROVA DE MATEMÁTICA (IV SIMULADO ITA/00) GABARITO COMENTÁRIO QUESTÕES OBJETIVAS QUESTÃO 0 LETRA D Como a equação é do quinto grau
D: 00 08 º EM MATEMÁTICA ITA IME SIMUL COMENT Rosângela o Ensino Médio PROVA DE MATEMÁTICA (IV SIMULADO ITA/00) GABARITO COMENTÁRIO QUESTÕES OBJETIVAS QUESTÃO 0 LETRA D Como a equação é do quinto grau
Módulo de Semelhança de Triângulos e Teorema de Tales. Semelhanças entre Figuras e Poĺıgonos. 8 o ano/9 a série E.F.
 Módulo de Semelhança de Triângulos e Teorema de Tales Semelhanças entre Figuras e Poĺıgonos. 8 o ano/9 a série E.F. Semelhança de Triângulos e Teorema de Tales Semelhanças entre Figuras e Polígonos. 1
Módulo de Semelhança de Triângulos e Teorema de Tales Semelhanças entre Figuras e Poĺıgonos. 8 o ano/9 a série E.F. Semelhança de Triângulos e Teorema de Tales Semelhanças entre Figuras e Polígonos. 1
54 CAPÍTULO 2. GEOMETRIA ANALÍTICA ( ) =
 54 CAPÍTULO. GEOMETRIA ANALÍTICA.5 Cônicas O grá co da equação + + + + + = 0 (.4) onde,,,, e são constantes com, e, não todos nulos, é uma cônica. A equação (.4) é chamada de equação geral do grau em e
54 CAPÍTULO. GEOMETRIA ANALÍTICA.5 Cônicas O grá co da equação + + + + + = 0 (.4) onde,,,, e são constantes com, e, não todos nulos, é uma cônica. A equação (.4) é chamada de equação geral do grau em e
Resposta de alguns exercícios pares do Simmons - Capítulo 1
 Seção 2 Ex. 2a x < 0 ou x > 1. Ex. 2b. -1 < x < 0 ou 0 < x < 1. Ex. 2c. -2 < x < 1. Ex. 2d. x -1 ou x 2. Ex. 2e. x = 0 ou x 1. Ex. 2f. x = -1/2 ou x -1. Ex. 2g. x < -7 ou x > 3. Ex. 2h. -3/2 < x < 1. Ex.
Seção 2 Ex. 2a x < 0 ou x > 1. Ex. 2b. -1 < x < 0 ou 0 < x < 1. Ex. 2c. -2 < x < 1. Ex. 2d. x -1 ou x 2. Ex. 2e. x = 0 ou x 1. Ex. 2f. x = -1/2 ou x -1. Ex. 2g. x < -7 ou x > 3. Ex. 2h. -3/2 < x < 1. Ex.
UFBA / UFRB a Fase Matemática RESOLUÇÃO: Professora Maria Antônia Gouveia. QUESTÕES de 01 a 08
 UFBA / UFRB 008 1a Fase Matemática Professora Maria Antônia Gouveia QUESTÕES de 01 a 08 INSTRUÇÃO: Assinale as proposições verdadeiras, some os números a elas associados e marque o resultado na Folha de
UFBA / UFRB 008 1a Fase Matemática Professora Maria Antônia Gouveia QUESTÕES de 01 a 08 INSTRUÇÃO: Assinale as proposições verdadeiras, some os números a elas associados e marque o resultado na Folha de
Geometria Analítica - Aula
 Geometria Analítica - Aula 18 228 IM-UFF K. Frensel - J. Delgado Aula 19 Continuamos com o nosso estudo da equação Ax 2 + Cy 2 + Dx + Ey + F = 0 1. Hipérbole Definição 1 Uma hipérbole, H, de focos F 1
Geometria Analítica - Aula 18 228 IM-UFF K. Frensel - J. Delgado Aula 19 Continuamos com o nosso estudo da equação Ax 2 + Cy 2 + Dx + Ey + F = 0 1. Hipérbole Definição 1 Uma hipérbole, H, de focos F 1
UFMG º DIA MATEMÁTICA BERNOULLI COLÉGIO E PRÉ-VESTIBULAR
 UFMG - 2003 4º DIA MATEMÁTICA BERNOULLI COLÉGIO E PRÉ-VESTIBULAR Matemática Questão 01 Sejam f(x) = x 2 + 3x + 4 e g(x) = ax + b duas funções. DETERMINE as constantes reais a e b para que (f. g)(x) = (g.
UFMG - 2003 4º DIA MATEMÁTICA BERNOULLI COLÉGIO E PRÉ-VESTIBULAR Matemática Questão 01 Sejam f(x) = x 2 + 3x + 4 e g(x) = ax + b duas funções. DETERMINE as constantes reais a e b para que (f. g)(x) = (g.
3 O ANO EM. Lista 19. Matemática II. f(x) g (x). g, 0,g 1 R R as seguintes funções: x 2 x 2 g 0(x) 2 g 0(4x 6) g 0(4x 6) g 1(x) 2 RAPHAEL LIMA
 3 O ANO EM Matemática II RAPHAEL LIMA Lista 19 1. (Pucrj 017) Dadas as funções f,g R R definidas por f(x) x 13x 36 - e g(x) - x 1. a) Encontre os pontos de interseção dos gráficos das duas funções. b)
3 O ANO EM Matemática II RAPHAEL LIMA Lista 19 1. (Pucrj 017) Dadas as funções f,g R R definidas por f(x) x 13x 36 - e g(x) - x 1. a) Encontre os pontos de interseção dos gráficos das duas funções. b)
NOME: ANO: 3º Nº: PROFESSOR(A):
 NOME: ANO: º Nº: PROFESSOR(A): Ana Luiza Ozores DATA: Algumas definições Triângulos: REVISÃO Lista 06 Triângulos e Quadriláteros Classificação quanto aos lados: Escaleno (todos os lados diferentes), Isósceles
NOME: ANO: º Nº: PROFESSOR(A): Ana Luiza Ozores DATA: Algumas definições Triângulos: REVISÃO Lista 06 Triângulos e Quadriláteros Classificação quanto aos lados: Escaleno (todos os lados diferentes), Isósceles
Usando estas propriedades, provamos que:
 Áreas de Polígonos Função área Uma função área é uma função que a cada região delimitada por um polígono, associa um número real com as seguintes propriedades: Regiões delimitada por polígonos congruentes
Áreas de Polígonos Função área Uma função área é uma função que a cada região delimitada por um polígono, associa um número real com as seguintes propriedades: Regiões delimitada por polígonos congruentes
XXVII OLIMPÍADA BRASILEIRA DE MATEMÁTICA PRIMEIRA FASE NÍVEL 3 (Ensino Médio) GABARITO
 XXVII OLIPÍADA BRASILEIRA DE ATEÁTICA PRIEIRA FASE NÍVEL 3 (Ensino édio) GABARITO GABARITO NÍVEL 3 1) D 6) C 11) C 16) D 1) C ) C 7) B 1) C 17) C ) Anulada 3) Anulada 8) D 13) B 18) A 3) B ) B 9) B 1)
XXVII OLIPÍADA BRASILEIRA DE ATEÁTICA PRIEIRA FASE NÍVEL 3 (Ensino édio) GABARITO GABARITO NÍVEL 3 1) D 6) C 11) C 16) D 1) C ) C 7) B 1) C 17) C ) Anulada 3) Anulada 8) D 13) B 18) A 3) B ) B 9) B 1)
Aula Exemplos e aplicações - continuação. Exemplo 8. Nesta aula continuamos com mais exemplos e aplicações dos conceitos vistos.
 Aula 1 Nesta aula continuamos com mais exemplos e aplicações dos conceitos vistos. 1. Exemplos e aplicações - continuação Exemplo 8 Considere o plano π : x + y + z = 3 e a reta r paralela ao vetor v =
Aula 1 Nesta aula continuamos com mais exemplos e aplicações dos conceitos vistos. 1. Exemplos e aplicações - continuação Exemplo 8 Considere o plano π : x + y + z = 3 e a reta r paralela ao vetor v =
Exercícios de Aprofundamento Matemática Geometria Analítica
 1. (Unicamp 015) Seja r a reta de equação cartesiana x y 4. Para cada número real t tal que 0 t 4, considere o triângulo T de vértices em (0, 0), (t, 0) e no ponto P de abscissa x t pertencente à reta
1. (Unicamp 015) Seja r a reta de equação cartesiana x y 4. Para cada número real t tal que 0 t 4, considere o triângulo T de vértices em (0, 0), (t, 0) e no ponto P de abscissa x t pertencente à reta
(b) Em quantos destes anagramas as letras CI aparecem juntas e nesta ordem? (c) Em quantos anagramas a letra A aparece antes (a esquerda) da letra E?
 Exercício 1. (a) Quantos são os anagramas da palavra CINEMA. (b) Em quantos destes anagramas as letras CI aparecem juntas e nesta ordem? (c) Em quantos anagramas a letra A aparece antes (a esquerda) da
Exercício 1. (a) Quantos são os anagramas da palavra CINEMA. (b) Em quantos destes anagramas as letras CI aparecem juntas e nesta ordem? (c) Em quantos anagramas a letra A aparece antes (a esquerda) da
MATEMÁTICA - 3o ciclo Circunferência - ângulos e arcos (9 o ano) Propostas de resolução
 MATEMÁTICA - 3o ciclo Circunferência - ângulos e arcos (9 o ano) Propostas de resolução Exercícios de provas nacionais e testes intermédios 1. Como o trapézio é isósceles, então BC = AD, pelo que também
MATEMÁTICA - 3o ciclo Circunferência - ângulos e arcos (9 o ano) Propostas de resolução Exercícios de provas nacionais e testes intermédios 1. Como o trapézio é isósceles, então BC = AD, pelo que também
Lista 3 com respostas
 Lista 3 com respostas Professora Nataliia Goloshchapova MAT0105-1 semestre de 2018 Exercício 1. Sendo que w = ( u v) ( u + v), determine o ângulo entre os vetores u e v, sabendo que u = v = w = 1 e u v
Lista 3 com respostas Professora Nataliia Goloshchapova MAT0105-1 semestre de 2018 Exercício 1. Sendo que w = ( u v) ( u + v), determine o ângulo entre os vetores u e v, sabendo que u = v = w = 1 e u v
Gabarito: 1 3r 4r 5r 6 r. 2. 3r 4r ,5 m. 45 EG m, constituem uma. AA' AP 8km. Resposta da questão 1: [C]
![Gabarito: 1 3r 4r 5r 6 r. 2. 3r 4r ,5 m. 45 EG m, constituem uma. AA' AP 8km. Resposta da questão 1: [C] Gabarito: 1 3r 4r 5r 6 r. 2. 3r 4r ,5 m. 45 EG m, constituem uma. AA' AP 8km. Resposta da questão 1: [C]](/thumbs/83/87180080.jpg) Gabarito: Resposta da questão 1: [C] Sejam x, x r e x r as medidas, em metros, dos lados do triângulo, com x, r 0. Aplicando o Teorema de Pitágoras, encontramos x r. Logo, os lados do triângulo medem r,
Gabarito: Resposta da questão 1: [C] Sejam x, x r e x r as medidas, em metros, dos lados do triângulo, com x, r 0. Aplicando o Teorema de Pitágoras, encontramos x r. Logo, os lados do triângulo medem r,
02 Do ponto P exterior a uma circunferência tiramos uma secante que corta a
 01 Em um triângulo AB AC 5 cm e BC cm. Tomando-se sobre AB e AC os pontos D e E, respectivamente, de maneira que DE seja paralela a BC e que o quadrilátero BCED seja circunscritível a um círculo, a distância
01 Em um triângulo AB AC 5 cm e BC cm. Tomando-se sobre AB e AC os pontos D e E, respectivamente, de maneira que DE seja paralela a BC e que o quadrilátero BCED seja circunscritível a um círculo, a distância
Aula 10 Triângulo Retângulo
 Aula 10 Triângulo Retângulo Projeção ortogonal Em um plano, consideremos um ponto e uma reta. Chama-se projeção ortogonal desse ponto sobre essa reta o pé da perpendicular traçada do ponto à reta. Na figura,
Aula 10 Triângulo Retângulo Projeção ortogonal Em um plano, consideremos um ponto e uma reta. Chama-se projeção ortogonal desse ponto sobre essa reta o pé da perpendicular traçada do ponto à reta. Na figura,
UFRJ - Instituto de Matemática
 UFRJ - Instituto de Matemática Programa de Pós-Graduação em Ensino de Matemática www.pg.im.ufrj.br/pemat Mestrado em Ensino de Matemática Seleção 9 Etapa Questão. Determine se as afirmações abaio são verdadeiras
UFRJ - Instituto de Matemática Programa de Pós-Graduação em Ensino de Matemática www.pg.im.ufrj.br/pemat Mestrado em Ensino de Matemática Seleção 9 Etapa Questão. Determine se as afirmações abaio são verdadeiras
Colégio Naval 2003 (prova verde)
 Colégio Naval 00 (prova verde) 01) Analise as seguintes afirmativas sobre um sistema S se duas equações do primeiro grau com duas incógnitas X e Y. I - S sempre terá ao menos uma solução, se os seus termos
Colégio Naval 00 (prova verde) 01) Analise as seguintes afirmativas sobre um sistema S se duas equações do primeiro grau com duas incógnitas X e Y. I - S sempre terá ao menos uma solução, se os seus termos
MAT-230 Diurno 1ª Folha de Exercícios
 MAT-230 Diurno 1ª Folha de Exercícios Prof. Paulo F. Leite agosto de 2009 1 Problemas de Geometria 1. Num triângulo isósceles a mediana, a bissetriz e a altura relativas à base coincidem. 2. Sejam A e
MAT-230 Diurno 1ª Folha de Exercícios Prof. Paulo F. Leite agosto de 2009 1 Problemas de Geometria 1. Num triângulo isósceles a mediana, a bissetriz e a altura relativas à base coincidem. 2. Sejam A e
Soluções Comentadas Matemática Curso Mentor Escola de Especialistas da Aeronáutica. Barbosa, L.S.
 Soluções Comentadas Matemática Curso Mentor Escola de Especialistas da Aeronáutica Barbosa, L.S. leonardosantos.inf@gmail.com 4 de junho de 014 Sumário I Provas 5 1 Matemática 013 1 7 II Soluções 11 Matemática
Soluções Comentadas Matemática Curso Mentor Escola de Especialistas da Aeronáutica Barbosa, L.S. leonardosantos.inf@gmail.com 4 de junho de 014 Sumário I Provas 5 1 Matemática 013 1 7 II Soluções 11 Matemática
Roteiro da segunda aula presencial - ME
 PIF Enumerabilidade Teoria dos Números Congruência Matemática Elementar Departamento de Matemática Universidade Federal da Paraíba 29 de outubro de 2014 PIF Enumerabilidade Teoria dos Números Congruência
PIF Enumerabilidade Teoria dos Números Congruência Matemática Elementar Departamento de Matemática Universidade Federal da Paraíba 29 de outubro de 2014 PIF Enumerabilidade Teoria dos Números Congruência
1º Banco de Questões do 4º Bimestre de Matemática (REVISÃO)
 Aluno(a): Professora: Deise Ilha Turno: Matutino. Componente Curricular: Matemática Data: / / 2016.. 1º Banco de Questões do 4º Bimestre de Matemática (REVISÃO) QUESTÃO 01 Tipo A (Julgar Certo ou Errado)
Aluno(a): Professora: Deise Ilha Turno: Matutino. Componente Curricular: Matemática Data: / / 2016.. 1º Banco de Questões do 4º Bimestre de Matemática (REVISÃO) QUESTÃO 01 Tipo A (Julgar Certo ou Errado)
Material Teórico - Módulo: Vetores em R 2 e R 3. Módulo e Produto Escalar - Parte 1. Terceiro Ano - Médio
 Material Teórico - Módulo: Vetores em R 2 e R 3 Módulo e Produto Escalar - Parte 1 Terceiro Ano - Médio Autor: Prof. Angelo Papa Neto Revisor: Prof. Antonio Caminha M. Neto 1 Módulo de um vetor O módulo
Material Teórico - Módulo: Vetores em R 2 e R 3 Módulo e Produto Escalar - Parte 1 Terceiro Ano - Médio Autor: Prof. Angelo Papa Neto Revisor: Prof. Antonio Caminha M. Neto 1 Módulo de um vetor O módulo
