Curvas Planas em Coordenadas Polares
|
|
|
- Thais Bennert Espírito Santo
- 7 Há anos
- Visualizações:
Transcrição
1 Curvas Planas em Coordenadas Polares Sumário. Coordenadas Polares Relações entre coordenadas polares e coordenadas cartesianas Exercícios
2 Unidade Coordenadas Polares Neste capítulo veremos que há outra maneira de expressar a posição de um ponto no plano, distinta da forma cartesiana. Embora os sistemas cartesianos sejam muito utilizados, há curvas no plano cuja equação toma um aspecto muito simples em relação a um referencial não cartesiano.. Coordenadas Polares Definição Um sistema de coordenadas polares ρ no plano consiste de um ponto, denominado pólo ou origem, de uma semirreta, com origem em, denominada eixo polar, e de uma unidade de comprimento utilizada para medir a distância de a um ponto qualquer do plano. Dado um ponto P do plano, suas coordenadas nesse sistema são ρ e, onde ρ é a distância de P a e é a medida do ângulo do eixo polar para a semirreta P. Escrevemos, então (Figura.): P = ( ρ, ) Convencionamos que a medida do ângulo tomada de sentido anti-horário é positiva, e negativa no sentido horário. P Figura.: Coordenadas polares. para P no primeira coordenada polar ρ de um ponto distinto do pólo é sempre maior que zero, pois representa a distância do ponto ao pólo. Mas podemos tomar também valores negativos para ρ, convencionando-se, neste caso, marcar a distância ρ na semirreta oposta à semirreta CD, ou seja, o ponto P = (ρ, ), com ρ < 0, corresponde ao ponto P = ( ρ, + π). Se a primeira coordenada polar de um ponto é zero, então esse ponto é o pólo. ângulo do P π ρ = ρ Figura.: (ρ, ) = ( ρ, + π) pólo não está denido. Convencionamos que (0, ) são as coordenadas polares do pólo, para todo ângulo. Podemos usar a medida dos ângulos em radianos ou em graus. Por exemplo, P = (, 30 ) = (, π/6).
3 Curvas Planas em Coordenadas Polares Unidade par (ρ, ) determina, de maneira única, um ponto do plano. No entanto, um ponto no plano pode ser determinado por meio de várias coordenadas polares distintas, pois, de acordo com a construção acima, as medidas e +πk, onde k Z, estão associadas ao mesmo ângulo e, portanto, (ρ, ) e (ρ, + πk) representam o mesmo ponto do plano. lém disto, como (ρ, ) = ( ρ, + π) se ρ < 0, então ( ρ, + π) = (ρ, + π) = (ρ, ) se ρ > 0. ssim, (ρ, ) = (ρ, + πk) = ( ρ, + (n + )π) quaisquer que sejam k, n Z e ρ R. Nisso, o sistma polar difere do sistema cartesiano, no qual existe uma correspondência biunívoca entre as coordenadas e os pontos do plano. Mas, se o ponto P não for a origem e se restringimos ρ e aos intervalos (0, + ) e [0, π), respectivamente, existirá apenas um par de coordenadas polares (ρ, ) para P. s pontos P = (, 0 ), P = (, π/), P 3 = (, 0 ) e P = (, π/3) estão ilustrados na gura.3. Exemplo π 3 P P 3 π P P Figura.3: Pontos P, P, P 3 e P no sistema ρ Podemos representar esses pontos também com as seguintes coordenadas polares: P = (, 360 k) = (, 360 n + 80 ); P = (, π/ + πk) = (, π/ + π + πn) = (, 3π/ + πn), P 3 = (, 360 k) = (, n) e P = (, π/3 + πk) = (, π/3 + π + πn) = (, π/3 + πn) = (, n) para todos k e n inteiros. 3
4 Unidade Coordenadas Polares Exemplo conjunto C dos pontos P = (ρ, ) que satsifazem a equação ρ = 3 é o conjunto dos pontos cuja distância ao pólo é igual a 3. u seja, C = {(ρ, ) ; ρ = 3 e R} ρ=3 P é o círculo de centro e raio igual a três. C Figura.: Círculo C bservação equação ρ = 3 também é uma equação polar do círculo acima. Em geral, ρ = a é a equação polar de um círculo de raio a centrado na origem. Exemplo 3 Seja r o conjunto dos pontos P = (ρ, ) do plano que satisfazem a equação polar = π, ou r seja, 0 = π r = {(ρ, ) ; ρ R e = π/}. Então, r é a reta que passa pelo pólo e tem inclinação 0 = π/ com respeito ao eixo polar. Figura.5: Reta r : = π/ bservação 3 Qualquer reta que passa pelo pólo tem equação polar da forma = 0, onde 0 é uma constante. lém disso, = 0 + πk e = 0 + (k + )π, k Z, representam a mesma reta no plano. Vamos obter agora a equação polar de uma reta r que não passa pelo pólo. Proposição Seja ρ um sistema de coordenadas polares no plano. Sejam r uma reta que não passa pelo pólo, λ a distância do pólo a r e α o ângulo que o eixo polar forma com a semirreta de origem no pólo que é perpendicular a r (Figura.6). Então, um ponto P de coordenadas polares (ρ, ) pertence a r se, e somente se: ρ cos( α) = λ (.)
5 Curvas Planas em Coordenadas Polares Unidade α λ=d(, r) Q r Figura.6: Reta r no sistema ρ Seja Q o ponto de interseção de r com a perpendicular a r contendo o pólo. Sabemos que P = (ρ, ) pertence a reta r se, e somente se, a projeção ortogonal do vetor P sobre o vetor Q coincide com Q, isto é: P r Proj Q P = Q. Seja β = P Q. Então, β = α ou β = α, dependendo da posição do ponto P (veja as guras.7), onde P = ( P, ) e Q = ( Q, α) são os pontos no sistema ρ. Note que cos β está bem denido, pois cos( α) = cos(α ). P r Demonstração β α Q α β Q r P Figura.7: Nas guras acima, a medida do ângulo α é tomada de para Q e a medida do ângulo é tomada de para P e Como concluímos: P = ρ, Q = λ, cos β = cos( α) = cos(α ), Proj Q P Q cos β P = Q Q = λ P (cos β) Q, 5
6 Unidade Coordenadas Polares Proj Q P = Q λ P cos β Q = Q λ P cos β = P cos β = λ ρ cos( α) = λ. Exemplo Seja ρ um sistema de coordenadas polares no plano. equação polar da reta r cuja distância ao pólo é igual a 3 tal que o ângulo que a semirreta perpendicular a r, com origem no pólo, forma com o eixo polar tem medida π/, é: r : ρ cos( π/) = 3. r π Figura.8: r : ρ cos( π/) = 3.. Relações entre coordenadas polares e coordenadas cartesianas. Seja ρ um sistema de coordenadas polares no plano. Consideremos o sistema cartesiano ortogonal tal que o eixo polar seja o semieixo positivo e o eixo seja obtido rotacionando de 90 o no sentido positivo. dmitamos a mesma unidade de medida nos dois sistemas (Figura.9). y =ρ sen ρ P x=ρ cos Figura.9: Sistemas de coordenadas; polar ρ e cartesiano Seja P um ponto no plano tal que P = (ρ, ), no sistema ρ, e P = (x, y), no sistema. Então, as relações entre essas coordenadas são dadas por: x = ρ cos e y = ρ sen (.) 6
7 Curvas Planas em Coordenadas Polares Unidade Dessas relações, obtemos: x = ρ cos, y = ρ sen, cos = x ρ, sen = y ρ e y x = sen cos = tg, de onde concluímos: cos = x x + y, sen = y x + y, ρ = x + y, e tg = y x (.3) De fato, para obter a primeira relação, basta observar que: x + y = ρ (cos + sen ) = ρ, o que implica ρ = ρ = x + y, pois ρ 0. s duas relações seguintes são substituições diretas da expressão de ρ em cos = x ρ e sen = y ρ. Podemos considerar também ρ = ρ = x + y. Neste caso, devemos considerar o ângulo tal que cos x = x + y e sen y = x + y para continuarem válidas as igualdades x = ρ cos e y = ρ sen. Como cos = cos e sen = sen, vemos que = + π, o que justica a convenção feita anteriormente que (ρ, ) e ( ρ, + π) representam o mesmo ponto em coordenadas polares. Convenção: Daqui em diante, sempre que zermos referência a um sistema polar ρ e a um sistema cartesiano, no mesmo contexto, admitiremos que o semieixo positivo é o eixo polar, caso este último não tenha sido denido explicitamente. Determine as coordenadas cartesianas ou polares dos seguintes pontos: (a) P = (ρ, ) = (, π/). Solução. Como ρ = e = π/, temos que x = ρ cos = cos π =0 y = ρ sen = sen π = são as coordenadas cartesianas de P. P Figura.0: P = (, π/) ρ e P = (0, ) Exemplo 5 7
8 Unidade Coordenadas Polares (b) P = (x, y) = (, ). Solução. Sendo x = e y =, temos que ρ = x + y = + =, cos = e sen =. Então, = π/ ou = π/ + πk, k Z, e P = (ρ, ) = (, π/) = (, π/ + πk) = (, 3π/ + πk), k Z, é o ponto P dado em coordenadas polares. (c) P = (ρ, ) = (, π/3). Solução. Sendo P = (, π/3) = (, π/3 + π) = (, π/3), temos que x = cos π/3 = cos π/3 =, y = sen π/3 = sen π/3 = 3 são as coordenadas cartesianas do ponto P. ρ= = π P Figura.: P = (, ) e P = (, π/) ρ π 3 P 3 π 3 Figura.: P = (, π/3) ρ e P = (, 3) (d) P = (x, y) = (, 5). Solução. Como x = e y = 5, temos que ρ = + 5 = = cos 0 = 5 sen 0 =. 5 ρ= = 0 P Portanto, (ρ, )=(, 0 )=(, 0 + π) Figura.3: P = (, 5) e é o ponto P dado em coordenadas polares. P = (, 0 ) ρ Exemplo 6 Seja r o lugar geométrico denido pela equação polar = 3π. Sabemos, pela denição de coordenadas polares, que r é o conjunto de todos os pontos P = (ρ, 3π/), com ρ R, tais que o ângulo entre o semieixo 8
9 Curvas Planas em Coordenadas Polares Unidade positivo e o vetor P é 3π, se ρ > 0, ou 7π, se ρ < 0. u seja, r é a reta que passa pela origem e tem coeciente angular igual a tg 3π = tg 7π =. P y Então, r : y = x. 3π u, usando a mudança de coordenadas (.3), obtemos também, substituindo y = tg na equação polar dada, que x y x = tg 3π = y = x. x 7π y x P Figura.: Reta = 3π. Seja r : x = a, com a 0, a reta vertical que corta o eixo no ponto (a, 0). Então, pela equação polar ρ cos( α) = λ de uma reta que passa pela origem, temos que r : ρ cos = a, pois α = 0 e λ = a se a > 0 ou, α = π e λ = a se a < 0. u, usando diretamente as equações de mudança de coordenadas (.), obtemos também r : ρ cos = a. r r Exemplo 7 π a a Figura.5: r : x = a, a > 0 Figura.6: r : x = a, a < 0 De modo análogo, podemos vericar que ρ sen = b é a equação polar da reta horizontal y = b que corta o eixo no ponto (0, b), com b 0. Seja r a reta de equação polar ρ cos( π/3) =. Pela Proposição, a reta l perpendicular à reta r, que passa pela origem, tem inclinação π/3 e intersecta r no ponto Q = (ρ 0, 0 ) = (, π/3). Logo, u = (cos π/3, sen π/3) = Exemplo 8 9
10 Unidade Coordenadas Polares (/, 3/) é um vetor normal a r e Q = (x o, y o ) = ( cos π/3, sen π/3) = (, 3) é um ponto de r. ssim, x 3 + y = x + 3 y = é a equação cartesiana de r. Podemos também encontrar a equação cartesiana de r da seguinte maneira. Pela identidade: cos(a b) = cos a cos b + sen a sen b, temos: ( ρ cos π ) = 3 ρ cos cos π 3 + ρ sen sen π 3 =. Logo, como x = ρ cos, y = ρ sen, cos π 3 = e sen π 3 3 =, segue que x + y 3 = x = 3 y =, é a equação cartesiana de r. l λ= α= π 3 Figura.7: Reta r r Exemplo 9 Seja a curva C de equação polar ρ = a cos, com a > 0. Utilizando as relações (.3) para obter a equação correspondente no sistema cartesiano, temos (Figura.8): ρ = a cos ± x + y ±x = a x + y x + y = ax. Completando o quadrado na última equação, obtemos: (x a) + y = a, que é a equação do círculo de centro (a, 0) e raio a. y =ρ sen a a ρ=a cos P x=ρ cos Figura.8: ρ = a cos. Em geral, o círculo no plano é caracterizado em termos das coordenadas polares de acordo com a seguinte proposição. 0
11 Curvas Planas em Coordenadas Polares Unidade Sejam ρ um sistema de coordenadas polares no plano, P 0 = (ρ 0, 0 ) ρ um ponto desse plano e r um valor positivo. Então o conjunto dos pontos P = (ρ, ) ρ que pertencem ao círculo de centro P 0 e raio r satisfazem a seguinte equação em coordenadas polares: Proposição 5 ρ + ρ 0 ρ 0 ρ cos( 0 ) = r Consideremos o sistema de coordenadas cartesianas tal que o eixo positivo coincida com o eixo polar e o eixo seja obtido rotacionando o eixo de 90 o no sentido positivo. No sistema, temos: P 0 = (ρ 0 cos 0, ρ 0 sen 0 ) e P = (ρ cos, ρ sen ). Sabemos que o círculo de centro P 0 e raio r é o conjunto dos pontos do plano cuja distância a P 0 é igual a r. Então: d(p, P 0 ) = r (ρ cos ρ 0 cos 0 ) + (ρ sen ρ 0 sen 0 ) = r ρ cos + ρ 0 cos 0 ρ 0 ρ cos 0 cos + ρ sen +ρ 0 sen 0 ρ 0 ρ sen 0 sen = r ρ (cos + sen ) + ρ 0 (cos 0 + sen 0 ) ρ 0 ρ (cos 0 cos + sen 0 sen ) = r ρ + ρ 0 ρ 0 ρ cos( 0 ) = r. Demonstração No desenvolvimento acima, calculamos a expressão da distância entre dois pontos em termos de coordenadas polares. Isto é, se P 0 = (ρ 0, 0 ) e P = (ρ, ), então: d(p 0, P ) = ρ 0 + ρ ρ 0 ρ cos( 0 ) bservação 6 Seja C um círculo que contém a origem e tem centro C = (a, b). Então, a sua equação cartesiana é Exemplo 0 x + y ax by = 0. (.) Pelas mudanças de coordenadas (.), temos que a equação (.), em coordenadas polares é
12 Unidade Coordenadas Polares ρ aρ cos bρ sen = 0 ρ(ρ a cos b sen ) = 0 ρ = 0 ou ρ = a cos + b sen. Como a equação ρ = 0 representa apenas a origem, que também satisfaz à equação ρ = a cos + b sen, pois = (0, 0 ), onde 0 é tal que cos 0 = b a + b e sen a 0 = a, obtemos que + b é uma equação polar de C. ρ = a cos + b sen (.5) Quando b = 0, a equação (.5) torna-se ρ = a cos que é uma equação polar do círculo C de centro (a, 0) e raio igual a a. Portanto, neste caso, C é tangente ao eixo na origem. C C a a a a Figura.9: C : ρ = a cos, a > 0 Figura.0: C : ρ = a cos, a < 0 Se a = 0, temos que C : ρ = a cos é uma equação polar do círculo de centro (0, b) e raio igual a b. Neste caso, C é tangente ao eixo na origem. b C b b b C Figura.: C : ρ = b sen, b > 0 Figura.: C : ρ = b sen, b < 0 Exemplo Considere o círculo C : (x ) + y = de centro C = (, 0) e raio igual a. Substituindo as relações ρ = x + y, x = ρ cos e y = ρ sen na equação cartesiana do círculo:
13 Curvas Planas em Coordenadas Polares Unidade (x ) + y = x + y x + = 0, obtemos que: ρ ρ cos + = 0 (.6) é a equação que relaciona as coordenadas polares de um ponto de C. círculo, (ρ 0, 0 ) = (, 0) é o centro dada em coordenadas polares. Logo, ρ = cos ± 6 cos 8 ρ = cos ± 6 sen ρ = cos ± sen. bserve que o discriminante da equação.6 é zero, se e somente se, sen = sen = ± = ± = ±π, e que a equação.6 tem duas soluções se, e somente se, sen > 0 sen < sen < y =x Nesse ( π, π ). P C C P y = x Figura.3: Círculo C e arcos C e C Note também que as retas r : y = x e r : y = x, que passam pela origem e fazem ângulos π/ e π/, respectivamente, com o semieixo positivo, são tangentes ao círculo C nos pontos P = (, ) e P = (, ), pois: e (x, y) C r x = y e (x ) + x = x = y e (x ) = 0 x = e y = (x, y) = (, ) = P, 3
14 Unidade Coordenadas Polares (x, y) C r x = y e (x ) + ( x) = x = y e (x ) = 0 x = e y = (x, y) = (, ) = P. ssim, ρ = cos [ sen, π, π ], é a equação polar do arco C, contido no semiplano x, e ρ = cos + ( sen, π, π ), é a equação polar C = C C. té agora esboçamos uma curva dada por sua equação polar apenas quando esta curva é uma reta ou um círculo. Para esboçarmos uma curva qualquer dada em coordenadas polares ou em coordenadas cartesianas, é bastante útil conhecer suas simetrias para simplicar a nossa análise. Dizemos que uma curva C é simétrica com respeito a uma reta l (ou a um ponto R) se, e somente se, para todo ponto P C, existir um ponto Q C tal que P e Q sejam simétricos em relação a l (a R, respectivamente). Logo, pelo visto nos Capítulos 9 e 0, uma curva C é simétrica com respeito ao eixo quando: (x, y) C (x, y) C; ao eixo quando: (x, y) C ( x, y) C; à origem quando: (x, y) C ( x, y) C; à reta y = x quando: (x, y) C (y, x) C; à reta y = x quando: (x, y) C ( y, x) C, onde (x, y) são as coordenadas cartesianas de um ponto. Então, se C é uma curva dada em coordenadas polares, temos que C é simétrica em relação ao eixo polar quando (ρ, + πk) C (ρ, ) C ou ( ρ, + π + πk) C para algum k Z. Com efeito, se (ρ, ) são as coordenadas polares de um ponto cujas coordenadas cartesianas são (x, y), então (ρ, + πk) e ( ρ, + π + πk), para todo inteiro k, são as coordenadas polares do ponto de coordenadas cartesianas (x, y) (Figura.).
15 Curvas Planas em Coordenadas Polares Unidade ρ (x, y) (x, y) Figura.: Simetria em relação ao eixo De modo análogo, podemos mostrar que uma curva C em coordenadas polares é simétrica à reta = π/ quando: (ρ, ) C (ρ, π + πk) C ou ( ρ, + πk) C, para algum k Z (Figura.5). à origem quando: (ρ, ) C (ρ, +π+πk) C ou ( ρ, +πk) C, para algum k Z (Figura.6). ( x, y) (x, y) (x, y) ρ ρ ρ ( x, y) Figura.5: Simetria em relação à reta = π/ Figura.6: Simetria em relação à origem à reta = π/ quando: (ρ, ) C (ρ, π/ +πk) C ou ( ρ, 3π/ + πk) C, para algum k Z (Figura.7). à reta = 3π/ quando: (ρ, ) C (ρ, 3π/ +πk) C ou ( ρ, π/ + πk) C, para algum k Z (Figura.8). 5
16 Unidade Coordenadas Polares (y, x) ( y, x) ρ ρ (x, y) (x, y) ρ ρ Figura.7: Simetria em relação à reta = π/ Figura.8: Simetria em relação à reta = 3π/ Exemplo curva C : ρ = cos é simétrica com respeito ao eixo polar (eixo ), pois (ρ, ) C se, e só se, (ρ, ) C. De fato, como cos( ) = cos, temos ρ = cos = cos( ). Mas, as coordenadas polares ( ρ, π ), que é outra representação do ponto (ρ, ), não satisfaz à equação polar de C, pois, caso contrário, teríamos ρ = cos(π ) = + cos, uma contradição, uma vez que ρ = cos. esboço desta curva será feito no Exemplo 3, item (a). Para testar as simetrias, é preferível, como mostra o exemplo acima, usar as coordenadas cartesianas de um ponto, devido à multiplicidade de possibilidades em coordenadas polares. No exemplo 3 faremos o esboço aproximado de algumas curvas dadas por suas equações em coordenadas polares. penas aproximado, porque, para fazermos um esboço ideal, precisaríamos analisar em quais intervalos do eixo (ou do eixo ) a curva é uma função crescente ou decrescente e convexa ou côncava da variável x (ou, respectivamente, da variável y). Exemplo 3 Faça um esboço da curva: (a) C : ρ = cos. Solução. Primeiro observe que ρ 0 para todo. Substituindo ρ = x + y x e cos = na equação polar de C, obtemos a equação x + y 6
17 Curvas Planas em Coordenadas Polares Unidade cartesiana da curva: C : x + y = x x + y C : x + y = x + y x C : (x + y + x) = x + y. Como (x, y) C (x, y) C, a curva é simétrica com respeito ao eixo. Então, para esboçá-la, basta analisar ρ = cos para [0, π], pois a função cos é periódica de período π. Uma vez que a função cos é decrescente no intervalo [0, π], variando de a quando varia de 0 a π, e cos π = 0, segue que ρ é decrescente no intervalo [I0, π], ρ = 0 se = 0, ρ = se = π, e ρ = se = π. ssim, o esboço de C, no intervalo [0, π], é o mostrado na Figura.9. C Figura.9: Curva C com [0, π] Pela simetria em relação ao eixo, o esboço de C é o dado na Figura.30. C Figura.30: Curva C com [0, π] É possível mostrar que ρ = cos é a equação polar de uma cardióide, estudada no Capítulo 0, tal que os círculos Γ e C têm raios iguais a e 7
18 Unidade Coordenadas Polares Γ está centrado no ponto (, 0). (b) C : ρ = + sen. Solução. Pela relação trigonométrica sen = sen cos, obtemos que ρ = + sen cos. lém disso, como ρ 0 para todo R, temos que x + y = + xy x + y (x + y ) 3/ = x + y + xy = (x + y). (.7) é a equação cartesiana da curva. Por (.7), é fácil vericar que a curva C é simétrica em relação à reta y = x (isto é, (x, y) C (y, x) C) e à reta y = x (isto é, (x, y) C ( y, x) [ C). Logo, basta analisar a curva ρ = +sen para no intervalo I = π, π ]. Temos que sen é uma função crescente que varia de a no intervalo I, sendo igual a zero para = 0. Logo, ρ = + sen é uma função crescente de no interalo I tal que ρ = 0 se = π/, ρ = se = 0 e ρ = se = π/. Então, o esboço de C no intervalo I é o mostrado na Figura.3. ρ= π Figura.3: Curva C [ no intervalo π, π ] Pelas simetrias da curva, é fácil ver que o esboço de C é o mostrado na Figura.3. 8
19 Curvas Planas em Coordenadas Polares Unidade π Figura.3: Curva C : ρ = + sen (c) C : ρ = + cos. Solução. Neste exemplo, ρ pode assumir valores negativos e positivos. Logo, ρ = ± x + y ±x e cos = x + y. Substituindo ρ e na equação dada, obtemos que ± x + y = ± x x + y x + y = ± x + y + x (x + y x) = x + y é a equação cartesiana da curva. É fácil vericar que esta curva é simétrica em relação ao eixo, mas não é simétrica em relação ao eixo. Portanto, para esboçá-la, basta variar o parâmetro no intervalo [0, π]. Para [0, π], temos: ρ = + cos = 0 se, e só se, cos =, ou seja, ρ = 0 se, e só se, 0 = π π 3 = π 3 ; ρ > 0 se, e só se, < cos, ou seja, se, e só se, 0 < π 3 ; ρ < 0 se, e só se, cos < π, ou seja, se, e só se, 3 < π. Tomando os pontos P = (3, 0), P = (, π/3), P 3 = (, π/), P = (0, π/3) e P 5 = (, π) em coordenadas polares da curva, podemos 9
20 Unidade Coordenadas Polares esboçar a parte da curva correspondente ao intervalo [0, π] (ver Fig..33). π 3 Figura.33: Curva C descrita variando em [0, π] bserve que o esboço da curva no intervalo [ π 3, π ], no qual ρ 0, é o simétrico, com respeito à origem, do gráco da curva {( ρ, ) ; ρ = + cos e [π/3, π]} (parte clara na Figura.5). Sendo a curva simétrica em relação ao eixo, obtemos o esboço completo da curva C (ver Fig..3). Figura.3: Curva C (d) C : ρ tg =. Solução. Sendo ρ = ± x + y e tg = y, obtemos que x ± x + y y x = ±y x + y = x y (x + y ) = x (.8) 0
21 Curvas Planas em Coordenadas Polares Unidade é a equação cartesiana de C. Como, pela equação (.8), a curva é simétrica com respeito aos eixos e, basta analizá-la no intervalo [0, π/]. Temos ρ = cos sen = 0 se = π, ρ é decrescente e positiva em (0, π/), cos e lim ρ() = lim =. lém disso, como x() = ρ() cos e sen y() = ρ() sen são as coordenadas cartesianas do ponto (ρ(), ), temos que cos lim x() = lim sen = + e lim y() = lim cos =, ou seja, y = é uma assíntota da curva C. Pelo obtido acima, vemos que Figura.35: Curva C variando em [0, π/] é o esboço de C no intervalo [0, π/]. Então, pela simetria da curva em relação aos eixos e, temos que o traço de C é o mostrado na Figura.36. Figura.36: Curva C
22 Unidade Exercícios. Exercícios. btenha as coordenadas polares dos pontos dados em coordenadas cartesianas, onde: = (, 3), B = ( 3, ), C = (, ), D = (, ), E = (0, ).. Encontre as coordenadas cartesianas dos pontos dados em coordenadas polares, onde: = (, π/6), B = ( 3, 0), C = (, π/), D = (, π/3), E = (3, 0 ), onde tg 0 = /3. 3. Determine a distância do ponto P ao ponto Q dados em coordenadas polares, onde: (a) P = (, π/) e Q = (3, π/); (b) P = (, 0 ) e Q = (, π/6), com tg 0 = 3/; (c) P = (6, 0 ) e Q = ( 6, ), com tg 0 = e tg = /.. Encontre a equação cartesiana e faça um esboço da curva polar: (a) C : ρ cos( π/) = ; (b) C : ρ = cos ; (c) C : ρ sen = ; (d) C : ρ + cos( π/3) = 3; (e) C : ρ = 3 cos sen ; (f) C : ρ = cos ; (g) C : ρ cos =. 5. Determine a equação cartesiana e as simetrias da curva C. Faça também um esboço de C. (a) C : ρ = 5 cos ; (b) C : ρ = cos ; (c) C : ρ = sen 3; (d) C : ρ( cos ) = ; (e) C : ρ = sec ; (f) C : ρ = tg. 6. Uma família de curvas tem equação polar C : ρ = m cos, com m R. + m cos Investigue como o traço de C muda quando o parâmetro m assume todos os valores reais. 7. Verique que as curvas polares ρ = + sen e ρ = sen possuem o mesmo traço.
23 Curvas Planas em Coordenadas Polares Unidade 8. Esboçe a região do plano que consiste dos pontos cujas coordenadas polares (ρ, ) satisfazem às inequações: (a) ρ 3; (b) ρ e π/ 3π/; (c) 0 ρ e π/ π/6; (d) ρ e π/3 π/3. 9. considere a região R do plano dada pelo sistema de inequações: x R : y 6 x 0 x 3. Faça um esboço de R e descreva-a como reunião de regiões na forma: ρ () ρ ρ (), onde (ρ, ) são as coordenadas polares de um ponto de R. 0. Descreva a região R como uma reunião de regiões na forma ρ () ρ ρ (), onde (ρ, ) são as coordenadas polares de um ponto de R, sendo: (a) R a região interior a ambas as curvas C : ρ = 3 cos e C : ρ = sen. (b) R a região limitada pelo círculo x + (y ) = e pelas retas y = x, y = x e x =, que contém o ponto (, 0), onde (x, y) são as coordenadas cartesianas de um ponto. 3
Capítulo 19. Coordenadas polares
 Capítulo 19 Coordenadas polares Neste capítulo, veremos que há outra maneira de expressar a posição de um ponto no plano, distinta da forma cartesiana. Embora os sistemas cartesianos sejam muito utilizados,
Capítulo 19 Coordenadas polares Neste capítulo, veremos que há outra maneira de expressar a posição de um ponto no plano, distinta da forma cartesiana. Embora os sistemas cartesianos sejam muito utilizados,
Aula 4. Coordenadas polares. Definição 1. Observação 1
 Aula Coordenadas polares Nesta aula veremos que há outra maneira de expressar a posição de um ponto no plano, distinta da forma cartesiana Embora os sistemas cartesianos sejam muito utilizados, há curvas
Aula Coordenadas polares Nesta aula veremos que há outra maneira de expressar a posição de um ponto no plano, distinta da forma cartesiana Embora os sistemas cartesianos sejam muito utilizados, há curvas
0 < c < a ; d(f 1, F 2 ) = 2c
 Capítulo 14 Elipse Nosso objetivo, neste e nos próximos capítulos, é estudar a equação geral do segundo grau em duas variáveis: Ax + Bxy + Cy + Dx + Ey + F = 0, onde A 0 ou B 0 ou C 0 Para isso, deniremos,
Capítulo 14 Elipse Nosso objetivo, neste e nos próximos capítulos, é estudar a equação geral do segundo grau em duas variáveis: Ax + Bxy + Cy + Dx + Ey + F = 0, onde A 0 ou B 0 ou C 0 Para isso, deniremos,
Equações paramétricas das cônicas
 Aula 1 Equações paramétricas das cônicas Ao estudarmos as retas no plano, vimos que a reta r que passa por dois pontos distintos P 1 = x 1, y 1 ) e P = x, y ) é dada pelas seguintes equações paramétricas:
Aula 1 Equações paramétricas das cônicas Ao estudarmos as retas no plano, vimos que a reta r que passa por dois pontos distintos P 1 = x 1, y 1 ) e P = x, y ) é dada pelas seguintes equações paramétricas:
Equações da reta no plano
 3 Equações da reta no plano Sumário 3.1 Introdução....................... 2 3.2 Equação paramétrica da reta............. 2 3.3 Equação cartesiana da reta.............. 7 3.4 Equação am ou reduzida da reta..........
3 Equações da reta no plano Sumário 3.1 Introdução....................... 2 3.2 Equação paramétrica da reta............. 2 3.3 Equação cartesiana da reta.............. 7 3.4 Equação am ou reduzida da reta..........
J. Delgado - K. Frensel - L. Crissaff Geometria Analítica e Cálculo Vetorial
 76 Capítulo 4 Distâncias no plano e regiões no plano 1. Distância de um ponto a uma reta Dados um ponto P e uma reta r no plano, já sabemos calcular a distância de P a cada ponto P r. Definição 1 Definimos
76 Capítulo 4 Distâncias no plano e regiões no plano 1. Distância de um ponto a uma reta Dados um ponto P e uma reta r no plano, já sabemos calcular a distância de P a cada ponto P r. Definição 1 Definimos
Posição relativa entre retas e círculos e distâncias
 4 Posição relativa entre retas e círculos e distâncias Sumário 4.1 Distância de um ponto a uma reta.......... 2 4.2 Posição relativa de uma reta e um círculo no plano 4 4.3 Distância entre duas retas no
4 Posição relativa entre retas e círculos e distâncias Sumário 4.1 Distância de um ponto a uma reta.......... 2 4.2 Posição relativa de uma reta e um círculo no plano 4 4.3 Distância entre duas retas no
A Reta no Espaço. Sumário
 16 A Reta no Espaço Sumário 16.1 Introdução....................... 2 16.2 Equações paramétricas da reta no espaço...... 2 16.3 Equação simétrica da reta no espaço........ 8 16.4 Exercícios........................
16 A Reta no Espaço Sumário 16.1 Introdução....................... 2 16.2 Equações paramétricas da reta no espaço...... 2 16.3 Equação simétrica da reta no espaço........ 8 16.4 Exercícios........................
Capítulo Equações da reta no espaço. Sejam A e B dois pontos distintos no espaço e seja r a reta que os contém. Então, P r existe t R tal que
 Capítulo 11 1. Equações da reta no espaço Sejam A e B dois pontos distintos no espaço e seja r a reta que os contém. Então, P r existe t R tal que AP = t AB Fig. 1: Reta r passando por A e B. Como o ponto
Capítulo 11 1. Equações da reta no espaço Sejam A e B dois pontos distintos no espaço e seja r a reta que os contém. Então, P r existe t R tal que AP = t AB Fig. 1: Reta r passando por A e B. Como o ponto
Capítulo 2. Retas no plano. 1. Retas verticais e não-verticais. Definição 1
 Capítulo 2 Retas no plano O objetivo desta aula é determinar a equação algébrica que representa uma reta no plano. Para isso, vamos analisar separadamente dois tipos de reta: reta vertical e reta não-vertical.
Capítulo 2 Retas no plano O objetivo desta aula é determinar a equação algébrica que representa uma reta no plano. Para isso, vamos analisar separadamente dois tipos de reta: reta vertical e reta não-vertical.
Aula Exemplos diversos. Exemplo 1
 Aula 3 1. Exemplos diversos Exemplo 1 Determine a equação da hipérbole equilátera, H, que passa pelo ponto Q = ( 1, ) e tem os eixos coordenados como assíntotas. Como as assíntotas da hipérbole são os
Aula 3 1. Exemplos diversos Exemplo 1 Determine a equação da hipérbole equilátera, H, que passa pelo ponto Q = ( 1, ) e tem os eixos coordenados como assíntotas. Como as assíntotas da hipérbole são os
Equação Geral do Segundo Grau em R 2
 8 Equação Geral do Segundo Grau em R Sumário 8.1 Introdução....................... 8. Autovalores e autovetores de uma matriz real 8.3 Rotação dos Eixos Coordenados........... 5 8.4 Formas Quadráticas..................
8 Equação Geral do Segundo Grau em R Sumário 8.1 Introdução....................... 8. Autovalores e autovetores de uma matriz real 8.3 Rotação dos Eixos Coordenados........... 5 8.4 Formas Quadráticas..................
Obter as equações paramétricas das cônicas.
 MÓDULO 1 - AULA 1 Aula 1 Equações paramétricas das cônicas Objetivo Obter as equações paramétricas das cônicas. Estudando as retas no plano, você viu que a reta s, determinada pelos pontos P = (x 1, y
MÓDULO 1 - AULA 1 Aula 1 Equações paramétricas das cônicas Objetivo Obter as equações paramétricas das cônicas. Estudando as retas no plano, você viu que a reta s, determinada pelos pontos P = (x 1, y
Distância entre duas retas. Regiões no plano
 Capítulo 4 Distância entre duas retas. Regiões no plano Nesta aula, veremos primeiro como podemos determinar a distância entre duas retas paralelas no plano. Para isso, lembramos que, na aula anterior,
Capítulo 4 Distância entre duas retas. Regiões no plano Nesta aula, veremos primeiro como podemos determinar a distância entre duas retas paralelas no plano. Para isso, lembramos que, na aula anterior,
J. Delgado - K. Frensel - L. Crissaff Geometria Analítica e Cálculo Vetorial
 178 Capítulo 10 Equação da reta e do plano no espaço 1. Equações paramétricas da reta no espaço Sejam A e B dois pontos distintos no espaço e seja r a reta que os contém. Então, P r existe t R tal que
178 Capítulo 10 Equação da reta e do plano no espaço 1. Equações paramétricas da reta no espaço Sejam A e B dois pontos distintos no espaço e seja r a reta que os contém. Então, P r existe t R tal que
Geometria Analítica I
 Geom. Analítica I Respostas do Módulo I - Aula 11 1 Geometria Analítica I 10/05/011 Respostas dos Exercícios do Módulo I - Aula 11 Aula 11 1. Em todos os itens desta questão, utilizaremos as relações x
Geom. Analítica I Respostas do Módulo I - Aula 11 1 Geometria Analítica I 10/05/011 Respostas dos Exercícios do Módulo I - Aula 11 Aula 11 1. Em todos os itens desta questão, utilizaremos as relações x
Geometria Analítica II - Aula 4 82
 Geometria Analítica II - Aula 4 8 IM-UFF K. Frensel - J. Delgado Aula 5 Esferas Iniciaremos o nosso estudo sobre superfícies com a esfera, que já nos é familiar. A esfera S de centro no ponto A e raio
Geometria Analítica II - Aula 4 8 IM-UFF K. Frensel - J. Delgado Aula 5 Esferas Iniciaremos o nosso estudo sobre superfícies com a esfera, que já nos é familiar. A esfera S de centro no ponto A e raio
O Plano no Espaço. Sumário
 17 Sumário 17.1 Introdução....................... 2 17.2 Equações paramétricas do plano no espaço..... 2 17.3 Equação cartesiana do plano............. 15 17.4 Exercícios........................ 21 1 Unidade
17 Sumário 17.1 Introdução....................... 2 17.2 Equações paramétricas do plano no espaço..... 2 17.3 Equação cartesiana do plano............. 15 17.4 Exercícios........................ 21 1 Unidade
Aula Distância entre duas retas paralelas no espaço. Definição 1. Exemplo 1
 Aula 1 Sejam r 1 = P 1 + t v 1 t R} e r 2 = P 2 + t v 2 t R} duas retas no espaço. Se r 1 r 2, sabemos que r 1 e r 2 são concorrentes (isto é r 1 r 2 ) ou não se intersectam. Quando a segunda possibilidade
Aula 1 Sejam r 1 = P 1 + t v 1 t R} e r 2 = P 2 + t v 2 t R} duas retas no espaço. Se r 1 r 2, sabemos que r 1 e r 2 são concorrentes (isto é r 1 r 2 ) ou não se intersectam. Quando a segunda possibilidade
Geometria Analítica II - Aula
 Geometria Analítica II - Aula 0 94 Aula Coordenadas Cilíndricas e Esféricas Para descrever de modo mais simples algumas curvas e regiões no plano introduzimos anteriormente as coordenadas polares. No espaço
Geometria Analítica II - Aula 0 94 Aula Coordenadas Cilíndricas e Esféricas Para descrever de modo mais simples algumas curvas e regiões no plano introduzimos anteriormente as coordenadas polares. No espaço
Coordenadas e distância na reta e no plano
 Capítulo 1 Coordenadas e distância na reta e no plano 1. Introdução A Geometria Analítica nos permite representar pontos da reta por números reais, pontos do plano por pares ordenados de números reais
Capítulo 1 Coordenadas e distância na reta e no plano 1. Introdução A Geometria Analítica nos permite representar pontos da reta por números reais, pontos do plano por pares ordenados de números reais
21 e 22. Superfícies Quádricas. Sumário
 21 e 22 Superfícies uádricas Sumário 21.1 Introdução....................... 2 21.2 Elipsoide........................ 3 21.3 Hiperboloide de uma Folha.............. 4 21.4 Hiperboloide de duas folhas..............
21 e 22 Superfícies uádricas Sumário 21.1 Introdução....................... 2 21.2 Elipsoide........................ 3 21.3 Hiperboloide de uma Folha.............. 4 21.4 Hiperboloide de duas folhas..............
Hipérbole. Sumário. 6.1 Introdução Hipérbole Forma canônica da hipérbole... 6
 6 Hipérbole Sumário 6.1 Introdução....................... 2 6.2 Hipérbole........................ 2 6.3 Forma canônica da hipérbole............. 6 6.3.1 Hipérbole com centro na origem e reta focal coincidente
6 Hipérbole Sumário 6.1 Introdução....................... 2 6.2 Hipérbole........................ 2 6.3 Forma canônica da hipérbole............. 6 6.3.1 Hipérbole com centro na origem e reta focal coincidente
Aula 32 Curvas em coordenadas polares
 MÓDULO 3 - AULA 32 Aula 32 Curvas em coordenadas polares Objetivo Aprender a usar as coordenadas polares para representar curvas planas. As coordenadas polares nos dão uma maneira alternativa de localizar
MÓDULO 3 - AULA 32 Aula 32 Curvas em coordenadas polares Objetivo Aprender a usar as coordenadas polares para representar curvas planas. As coordenadas polares nos dão uma maneira alternativa de localizar
Parametrização de algumas curvas planas
 Aula 3 Parametrização de algumas curvas planas Nesta aula veremos como obter equações paramétricas de algumas curvas planas, usando relações trigonométricas básicas e observando as condições que um ponto
Aula 3 Parametrização de algumas curvas planas Nesta aula veremos como obter equações paramétricas de algumas curvas planas, usando relações trigonométricas básicas e observando as condições que um ponto
Aula 10 Regiões e inequações no plano
 MÓDULO 1 - AULA 10 Aula 10 Regiões e inequações no plano Objetivos Resolver inequações do segundo grau. Analisar sistemas envolvendo inequações do primeiro e segundo graus. Resolver inequações modulares
MÓDULO 1 - AULA 10 Aula 10 Regiões e inequações no plano Objetivos Resolver inequações do segundo grau. Analisar sistemas envolvendo inequações do primeiro e segundo graus. Resolver inequações modulares
Produto interno e produto vetorial no espaço
 14 Produto interno e produto vetorial no espaço Sumário 14.1 Produto interno.................... 14. Produto vetorial.................... 5 14..1 Interpretação geométrica da norma do produto vetorial.......................
14 Produto interno e produto vetorial no espaço Sumário 14.1 Produto interno.................... 14. Produto vetorial.................... 5 14..1 Interpretação geométrica da norma do produto vetorial.......................
Equações Paramétricas e Coordenadas Polares. Copyright Cengage Learning. Todos os direitos reservados.
 10 Equações Paramétricas e Coordenadas Polares Copyright Cengage Learning. Todos os direitos reservados. 10.3 Coordenadas Polares Copyright Cengage Learning. Todos os direitos reservados. Coordenadas Polares
10 Equações Paramétricas e Coordenadas Polares Copyright Cengage Learning. Todos os direitos reservados. 10.3 Coordenadas Polares Copyright Cengage Learning. Todos os direitos reservados. Coordenadas Polares
Geometria Analítica - Aula
 Geometria Analítica - Aula 18 228 IM-UFF K. Frensel - J. Delgado Aula 19 Continuamos com o nosso estudo da equação Ax 2 + Cy 2 + Dx + Ey + F = 0 1. Hipérbole Definição 1 Uma hipérbole, H, de focos F 1
Geometria Analítica - Aula 18 228 IM-UFF K. Frensel - J. Delgado Aula 19 Continuamos com o nosso estudo da equação Ax 2 + Cy 2 + Dx + Ey + F = 0 1. Hipérbole Definição 1 Uma hipérbole, H, de focos F 1
Retas e círculos, posições relativas e distância de um ponto a uma reta
 Capítulo 3 Retas e círculos, posições relativas e distância de um ponto a uma reta Nesta aula vamos caracterizar de forma algébrica a posição relativa de duas retas no plano e de uma reta e de um círculo
Capítulo 3 Retas e círculos, posições relativas e distância de um ponto a uma reta Nesta aula vamos caracterizar de forma algébrica a posição relativa de duas retas no plano e de uma reta e de um círculo
Aula Elipse. Definição 1. Nosso objetivo agora é estudar a equação geral do segundo grau em duas variáveis:
 Aula 18 Nosso objetivo agora é estudar a equação geral do segundo grau em duas variáveis: Ax + Bxy + Cy + Dx + Ey + F = 0, onde A 0 ou B 0 ou C 0 Vamos considerar primeiro os casos em que B = 0. Isto é,
Aula 18 Nosso objetivo agora é estudar a equação geral do segundo grau em duas variáveis: Ax + Bxy + Cy + Dx + Ey + F = 0, onde A 0 ou B 0 ou C 0 Vamos considerar primeiro os casos em que B = 0. Isto é,
Coordenadas Polares. Exemplos: Representar em um sistema de coordenadas polares, os seguintes pontos: d) P 4,
 Coordenadas Polares Existem vários sistemas de coordenadas que mostram a posição de um ponto em um plano. O sistema de coordenadas polares é um deles. No sistema cartesiano, as coordenadas são números
Coordenadas Polares Existem vários sistemas de coordenadas que mostram a posição de um ponto em um plano. O sistema de coordenadas polares é um deles. No sistema cartesiano, as coordenadas são números
Aula 2 A distância no espaço
 MÓDULO 1 - AULA 2 Objetivos Aula 2 A distância no espaço Determinar a distância entre dois pontos do espaço. Estabelecer a equação da esfera em termos de distância. Estudar a posição relativa entre duas
MÓDULO 1 - AULA 2 Objetivos Aula 2 A distância no espaço Determinar a distância entre dois pontos do espaço. Estabelecer a equação da esfera em termos de distância. Estudar a posição relativa entre duas
10. Determine as equações cartesianas das famílias de retas que fazem um ângulo de π/4 radianos com a reta y = 2x + 1.
 Geometria Analítica. 1. Determine as posições relativas e as interseções entre os conjuntos em R abaixo. Em cada item também faça um esboço dos dois conjuntos dados no mesmo sistema de eixos. (a) C : (x
Geometria Analítica. 1. Determine as posições relativas e as interseções entre os conjuntos em R abaixo. Em cada item também faça um esboço dos dois conjuntos dados no mesmo sistema de eixos. (a) C : (x
Objetivos. em termos de produtos internos de vetores.
 Aula 5 Produto interno - Aplicações MÓDULO 1 - AULA 5 Objetivos Calcular áreas de paralelogramos e triângulos. Calcular a distância de um ponto a uma reta e entre duas retas. Determinar as bissetrizes
Aula 5 Produto interno - Aplicações MÓDULO 1 - AULA 5 Objetivos Calcular áreas de paralelogramos e triângulos. Calcular a distância de um ponto a uma reta e entre duas retas. Determinar as bissetrizes
Aula 10 Produto interno, vetorial e misto -
 MÓDULO 2 - AULA 10 Aula 10 Produto interno, vetorial e misto - Aplicações II Objetivos Estudar as posições relativas entre retas no espaço. Obter as expressões para calcular distância entre retas. Continuando
MÓDULO 2 - AULA 10 Aula 10 Produto interno, vetorial e misto - Aplicações II Objetivos Estudar as posições relativas entre retas no espaço. Obter as expressões para calcular distância entre retas. Continuando
Coordenadas Polares. Exemplos: Representar em um sistema de coordenadas polares, os seguintes pontos: d) P 4,
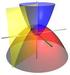 Cálculo II Profa. Adriana Cherri 1 Coordenadas Polares Existem vários sistemas de coordenadas que mostram a posição de um ponto em um plano. O sistema de coordenadas polares é um deles. No sistema cartesiano,
Cálculo II Profa. Adriana Cherri 1 Coordenadas Polares Existem vários sistemas de coordenadas que mostram a posição de um ponto em um plano. O sistema de coordenadas polares é um deles. No sistema cartesiano,
Geometria Analítica II - Aula 5 108
 Geometria Analítica II - Aula 5 108 IM-UFF Aula 6 Superfícies Cilíndricas Sejam γ uma curva contida num plano π do espaço e v 0 um vetor não-paralelo ao plano π. A superfície cilíndrica S de diretriz γ
Geometria Analítica II - Aula 5 108 IM-UFF Aula 6 Superfícies Cilíndricas Sejam γ uma curva contida num plano π do espaço e v 0 um vetor não-paralelo ao plano π. A superfície cilíndrica S de diretriz γ
Capítulo Coordenadas no Espaço. Seja E o espaço da Geometria Euclidiana tri-dimensional.
 Capítulo 9 1. Coordenadas no Espaço Seja E o espaço da Geometria Euclidiana tri-dimensional. Um sistema de eixos ortogonais OXY Z em E consiste de três eixos ortogonais entre si OX, OY e OZ com a mesma
Capítulo 9 1. Coordenadas no Espaço Seja E o espaço da Geometria Euclidiana tri-dimensional. Um sistema de eixos ortogonais OXY Z em E consiste de três eixos ortogonais entre si OX, OY e OZ com a mesma
Geometria Analítica II - Aula 7 178
 Geometria Analítica II - Aula 7 178 Aula 8 Superfícies Regradas Dizemos que uma superfície S é regrada quando por todo ponto P pertencente a S passa pelo menos uma reta r P inteiramente contida em S. Fig.
Geometria Analítica II - Aula 7 178 Aula 8 Superfícies Regradas Dizemos que uma superfície S é regrada quando por todo ponto P pertencente a S passa pelo menos uma reta r P inteiramente contida em S. Fig.
MAT CÁLCULO 2 PARA ECONOMIA. Geometria Analítica
 MT0146 - CÁLCULO PR ECONOMI SEMESTRE DE 016 LIST DE PROBLEMS Geometria nalítica 1) Sejam π 1 e π os planos de equações, respectivamente, x + y + z = e x y + z = 1. Seja r a reta formada pela interseção
MT0146 - CÁLCULO PR ECONOMI SEMESTRE DE 016 LIST DE PROBLEMS Geometria nalítica 1) Sejam π 1 e π os planos de equações, respectivamente, x + y + z = e x y + z = 1. Seja r a reta formada pela interseção
Sistemas de equações lineares com três variáveis
 18 Sistemas de equações lineares com três variáveis Sumário 18.1 Introdução....................... 18. Sistemas de duas equações lineares........... 18. Sistemas de três equações lineares........... 8
18 Sistemas de equações lineares com três variáveis Sumário 18.1 Introdução....................... 18. Sistemas de duas equações lineares........... 18. Sistemas de três equações lineares........... 8
1. Seja θ = ang (r, s). Calcule sen θ nos casos (a) e (b) e cos θ nos casos (c) e (d): = z 3 e s : { 3x + y 5z = 0 x 2y + 3z = 1
 14 a lista de exercícios - SMA0300 - Geometria Analítica Estágio PAE - Alex C. Rezende Medida angular, distância, mudança de coordenadas, cônicas e quádricas 1. Seja θ = ang (r, s). Calcule sen θ nos casos
14 a lista de exercícios - SMA0300 - Geometria Analítica Estágio PAE - Alex C. Rezende Medida angular, distância, mudança de coordenadas, cônicas e quádricas 1. Seja θ = ang (r, s). Calcule sen θ nos casos
MAT Poli Roteiro de Estudos sobre as Cônicas
 MAT25 - Poli - 2003 Roteiro de Estudos sobre as Cônicas Martha Salerno Monteiro Departamento de Matemática IME-USP Uma equação quadrática em duas variáveis é uma equação da forma a + by 2 + cxy + dx +
MAT25 - Poli - 2003 Roteiro de Estudos sobre as Cônicas Martha Salerno Monteiro Departamento de Matemática IME-USP Uma equação quadrática em duas variáveis é uma equação da forma a + by 2 + cxy + dx +
Aula 4 Produto Interno
 MÓDULO 1 - AULA 4 Objetivos Aula 4 Produto Interno Definir as noções de ângulo entre dois vetores, a norma de um vetor e a operação de produto interno. Compreender as propriedades básicas da norma e do
MÓDULO 1 - AULA 4 Objetivos Aula 4 Produto Interno Definir as noções de ângulo entre dois vetores, a norma de um vetor e a operação de produto interno. Compreender as propriedades básicas da norma e do
MAT Poli Cônicas - Parte I
 MAT2454 - Poli - 2011 Cônicas - Parte I Uma equação quadrática em duas variáveis, x e y, é uma equação da forma ax 2 +by 2 +cxy +dx+ey +f = 0, em que pelo menos um doscoeficientes a, b oucénão nulo 1.
MAT2454 - Poli - 2011 Cônicas - Parte I Uma equação quadrática em duas variáveis, x e y, é uma equação da forma ax 2 +by 2 +cxy +dx+ey +f = 0, em que pelo menos um doscoeficientes a, b oucénão nulo 1.
Lista 3: Geometria Analítica
 Lista 3: Geometria Analítica A. Ramos 25 de abril de 2017 Lista em constante atualização. 1. Equação da reta e do plano; 2. Ângulo entre retas e entre planos. Resumo Equação da reta Equação vetorial. Uma
Lista 3: Geometria Analítica A. Ramos 25 de abril de 2017 Lista em constante atualização. 1. Equação da reta e do plano; 2. Ângulo entre retas e entre planos. Resumo Equação da reta Equação vetorial. Uma
1 Distância entre dois pontos do plano
 Noções Topológicas do Plano Americo Cunha André Zaccur Débora Mondaini Ricardo Sá Earp Departamento de Matemática Pontifícia Universidade Católica do Rio de Janeiro 1 Distância entre dois pontos do plano
Noções Topológicas do Plano Americo Cunha André Zaccur Débora Mondaini Ricardo Sá Earp Departamento de Matemática Pontifícia Universidade Católica do Rio de Janeiro 1 Distância entre dois pontos do plano
Aula 15 Superfícies quádricas - cones quádricos
 Aula 15 Superfícies quádricas - cones quádricos MÓDULO - AULA 15 Objetivos Definir e estudar os cones quádricos identificando suas seções planas. Analisar os cones quádricos regrados e de revolução. Cones
Aula 15 Superfícies quádricas - cones quádricos MÓDULO - AULA 15 Objetivos Definir e estudar os cones quádricos identificando suas seções planas. Analisar os cones quádricos regrados e de revolução. Cones
SISTEMAS DE COORDENADAS
 1 SISTEMAS DE COORDENADAS 2.1 Coordenadas polares no R² Fonte: Cálculo A. Funções. Limite. Derivação. Integração. Diva Marília Flemming. Mírian Buss Gonçalves. Até o presente momento, localizamos um ponto
1 SISTEMAS DE COORDENADAS 2.1 Coordenadas polares no R² Fonte: Cálculo A. Funções. Limite. Derivação. Integração. Diva Marília Flemming. Mírian Buss Gonçalves. Até o presente momento, localizamos um ponto
Geometria Analítica. Katia Frensel - Jorge Delgado. NEAD - Núcleo de Educação a Distância. Curso de Licenciatura em Matemática UFMA
 Geometria Analítica NEAD - Núcleo de Educação a Distância Curso de Licenciatura em Matemática UFMA Katia Frensel - Jorge Delgado Março, 2011 ii Geometria Analítica Conteúdo Prefácio ix 1 Coordenadas na
Geometria Analítica NEAD - Núcleo de Educação a Distância Curso de Licenciatura em Matemática UFMA Katia Frensel - Jorge Delgado Março, 2011 ii Geometria Analítica Conteúdo Prefácio ix 1 Coordenadas na
Aula 4 Colinearidade, coplanaridade e dependência linear
 Aula 4 Colinearidade, coplanaridade e dependência linear MÓDULO 1 - AULA 4 Objetivos Compreender os conceitos de independência e dependência linear. Estabelecer condições para determinar quando uma coleção
Aula 4 Colinearidade, coplanaridade e dependência linear MÓDULO 1 - AULA 4 Objetivos Compreender os conceitos de independência e dependência linear. Estabelecer condições para determinar quando uma coleção
Geometria Analítica - Aula
 Geometria Analítica - Aula 19 246 IM-UFF K. Frensel - J. Delgado Aula 20 Vamos analisar a equação Ax 2 + Cy 2 + Dx + Ey + F = 0 nos casos em que exatamente um dos coeficientes A ou C é nulo. 1. Parábola
Geometria Analítica - Aula 19 246 IM-UFF K. Frensel - J. Delgado Aula 20 Vamos analisar a equação Ax 2 + Cy 2 + Dx + Ey + F = 0 nos casos em que exatamente um dos coeficientes A ou C é nulo. 1. Parábola
Capítulo 12. Ângulo entre duas retas no espaço. Definição 1. O ângulo (r1, r2 ) entre duas retas r1 e r2 é assim definido:
 Capítulo 1 1. Ângulo entre duas retas no espaço Definição 1 O ângulo (r1, r ) entre duas retas r1 e r é assim definido: (r1, r ) 0o se r1 e r são coincidentes, se as retas são concorrentes, isto é, r1
Capítulo 1 1. Ângulo entre duas retas no espaço Definição 1 O ângulo (r1, r ) entre duas retas r1 e r é assim definido: (r1, r ) 0o se r1 e r são coincidentes, se as retas são concorrentes, isto é, r1
6.1 equações canônicas de círculos e esferas
 6 C Í R C U LO S E E S F E R A S 6.1 equações canônicas de círculos e esferas Um círculo é o conjunto de pontos no plano que estão a uma certa distância r de um ponto dado (a, b). Desta forma temos que
6 C Í R C U LO S E E S F E R A S 6.1 equações canônicas de círculos e esferas Um círculo é o conjunto de pontos no plano que estão a uma certa distância r de um ponto dado (a, b). Desta forma temos que
Exercícios sobre Trigonometria
 Universidade Federal Fluminense Campus do Valonguinho Instituto de Matemática e Estatística Departamento de Matemática Aplicada - GMA Prof Saponga uff Rua Mário Santos Braga s/n 400-40 Niterói, RJ Tels:
Universidade Federal Fluminense Campus do Valonguinho Instituto de Matemática e Estatística Departamento de Matemática Aplicada - GMA Prof Saponga uff Rua Mário Santos Braga s/n 400-40 Niterói, RJ Tels:
Aula 14 Círculo. Objetivos
 Aula 1 Círculo MÓDULO 1 - AULA 1 Objetivos Determinar a equação do círculo de centro C e raio r, como um lugar geométrico. Aprender os conceitos de retas tangente e normal num ponto P de um círculo. Esboçar
Aula 1 Círculo MÓDULO 1 - AULA 1 Objetivos Determinar a equação do círculo de centro C e raio r, como um lugar geométrico. Aprender os conceitos de retas tangente e normal num ponto P de um círculo. Esboçar
Aula 6 Produto interno
 MÓDULO 1 - AULA 6 Objetivos Aula 6 Produto interno Estabelecer os conceitos de norma de um vetor e de ângulo entre dois vetores do espaço. Definir o produto interno de vetores no espaço e estabelecer suas
MÓDULO 1 - AULA 6 Objetivos Aula 6 Produto interno Estabelecer os conceitos de norma de um vetor e de ângulo entre dois vetores do espaço. Definir o produto interno de vetores no espaço e estabelecer suas
UNIVERSIDADE FEDERAL DE PERNAMBUCO
 CÁLCULO L1 NOTAS DA QUINTA AULA UNIVERSIDADE FEDERAL DE PERNAMBUCO Resumo. Iniciamos a aula definindo as funções trigonométricas e estabelecendo algumas de suas propriedades básicas. A seguir, calcularemos
CÁLCULO L1 NOTAS DA QUINTA AULA UNIVERSIDADE FEDERAL DE PERNAMBUCO Resumo. Iniciamos a aula definindo as funções trigonométricas e estabelecendo algumas de suas propriedades básicas. A seguir, calcularemos
MATEMÁTICA A - 12o Ano N o s Complexos - Conjuntos e condições Propostas de resolução
 MATEMÁTICA A - o Ano N o s Complexos - Conjuntos e condições Propostas de resolução Exercícios de exames e testes intermédios. Escrevendo i na f.t. temos i i = ρe iα, onde: ρ = i i = + ) = tg α = = ; como
MATEMÁTICA A - o Ano N o s Complexos - Conjuntos e condições Propostas de resolução Exercícios de exames e testes intermédios. Escrevendo i na f.t. temos i i = ρe iα, onde: ρ = i i = + ) = tg α = = ; como
MAT001 Cálculo Diferencial e Integral I
 1 MAT001 Cálculo Diferencial e Integral I GEOMETRIA ANALÍTICA Coordenadas de pontos no plano cartesiano Distâncias entre pontos Sejam e dois pontos no plano cartesiano A distância entre e é dada pela expressão
1 MAT001 Cálculo Diferencial e Integral I GEOMETRIA ANALÍTICA Coordenadas de pontos no plano cartesiano Distâncias entre pontos Sejam e dois pontos no plano cartesiano A distância entre e é dada pela expressão
MATEMÁTICA A - 12o Ano N o s Complexos - Conjuntos e condições Propostas de resolução
 MATEMÁTICA A - o Ano N o s Complexos - Conjuntos e condições Propostas de resolução Exercícios de exames e testes intermédios. Escrevendo i na f.t. temos i i = ρ cis α, onde: ρ = i i = + ) = tg α = = ;
MATEMÁTICA A - o Ano N o s Complexos - Conjuntos e condições Propostas de resolução Exercícios de exames e testes intermédios. Escrevendo i na f.t. temos i i = ρ cis α, onde: ρ = i i = + ) = tg α = = ;
Coordenadas e vetores no espaço
 13 Coordenadas e vetores no espaço Sumário 13.1 Coordenadas no espaço................ 2 13.2 Distância entre dois pontos do espaço........ 6 13.3 Vetores no espaço................... 10 13.4 Operações
13 Coordenadas e vetores no espaço Sumário 13.1 Coordenadas no espaço................ 2 13.2 Distância entre dois pontos do espaço........ 6 13.3 Vetores no espaço................... 10 13.4 Operações
Concluimos dai que o centro da circunferência é C = (6, 4) e o raio é
 QUESTÕES-AULA 17 1. A equação x 2 + y 2 12x + 8y + 0 = 0 representa uma circunferência de centro C = (a, b) e de raio R. Determinar o valor de a + b + R. Solução Completamos quadrados na expressão dada.
QUESTÕES-AULA 17 1. A equação x 2 + y 2 12x + 8y + 0 = 0 representa uma circunferência de centro C = (a, b) e de raio R. Determinar o valor de a + b + R. Solução Completamos quadrados na expressão dada.
54 CAPÍTULO 2. GEOMETRIA ANALÍTICA ( ) =
 54 CAPÍTULO. GEOMETRIA ANALÍTICA.5 Cônicas O grá co da equação + + + + + = 0 (.4) onde,,,, e são constantes com, e, não todos nulos, é uma cônica. A equação (.4) é chamada de equação geral do grau em e
54 CAPÍTULO. GEOMETRIA ANALÍTICA.5 Cônicas O grá co da equação + + + + + = 0 (.4) onde,,,, e são constantes com, e, não todos nulos, é uma cônica. A equação (.4) é chamada de equação geral do grau em e
PROPOSTA DE RESOLUÇÃO DA PROVA DE MATEMÁTICA A DO ENSINO SECUNDÁRIO (CÓDIGO DA PROVA 635) 2ª FASE 20 DE JULHO 2018 CADERNO 1
 PROPOSTA DE RESOLUÇÃO DA PROVA DE MATEMÁTICA A DO ENSINO SECUNDÁRIO (CÓDIGO DA PROVA 635) ª FASE 0 DE JULHO 08 CADERNO... P00/00 Como se trata de uma distribuição normal temos que: ( ) 0,9545. P µ σ
PROPOSTA DE RESOLUÇÃO DA PROVA DE MATEMÁTICA A DO ENSINO SECUNDÁRIO (CÓDIGO DA PROVA 635) ª FASE 0 DE JULHO 08 CADERNO... P00/00 Como se trata de uma distribuição normal temos que: ( ) 0,9545. P µ σ
MAT111 - Cálculo I - IF TRIGONOMETRIA. As Funçoes trigonométricas no triângulo retângulo
 MAT111 - Cálculo I - IF - 010 TRIGONOMETRIA As Funçoes trigonométricas no triângulo retângulo Analisando a figura a seguir, temos que os triângulos retângulos OA 1 B 1 e OA B, são semelhantes, pois possuem
MAT111 - Cálculo I - IF - 010 TRIGONOMETRIA As Funçoes trigonométricas no triângulo retângulo Analisando a figura a seguir, temos que os triângulos retângulos OA 1 B 1 e OA B, são semelhantes, pois possuem
Aula 17 Superfícies quádricas - parabolóides
 Objetivos Aula 17 Superfícies quádricas - parabolóides Apresentar os parabolóides elípticos e hiperbólicos identificando suas seções planas. Estudar os parabolóides regrados e de revolução. Nas superfícies
Objetivos Aula 17 Superfícies quádricas - parabolóides Apresentar os parabolóides elípticos e hiperbólicos identificando suas seções planas. Estudar os parabolóides regrados e de revolução. Nas superfícies
MATEMÁTICA A - 12o Ano N o s Complexos - Conjuntos e condições Propostas de resolução
 MATEMÁTICA A - o Ano N o s Complexos - Conjuntos e condições Propostas de resolução Exercícios de exames e testes intermédios. Analisando cada uma das afirmações temos (A) z z = z z é uma afirmação verdadeira
MATEMÁTICA A - o Ano N o s Complexos - Conjuntos e condições Propostas de resolução Exercícios de exames e testes intermédios. Analisando cada uma das afirmações temos (A) z z = z z é uma afirmação verdadeira
Sociedade Brasileira de Matemática Mestrado Profissional em Matemática em Rede Nacional
 Sociedade Brasileira de Matemática Mestrado Profissional em Matemática em Rede Nacional MA11 Números e Funções Reais Avaliação 2 GABARITO 22 de junho de 201 1. Em cada um dos itens abaixo, dê, se possível,
Sociedade Brasileira de Matemática Mestrado Profissional em Matemática em Rede Nacional MA11 Números e Funções Reais Avaliação 2 GABARITO 22 de junho de 201 1. Em cada um dos itens abaixo, dê, se possível,
Material Teórico - Redução ao Primeiro Quadrante e Funções Trigonométricas. Redução ao Primeiro Quadrante. Primeiro Ano do Ensino Médio
 Material Teórico - Redução ao rimeiro uadrante e Funções Trigonométricas Redução ao rimeiro uadrante rimeiro Ano do Ensino Médio Autor: rof. Fabrício Siqueira enevides Revisor: rof. Antonio Caminha M.
Material Teórico - Redução ao rimeiro uadrante e Funções Trigonométricas Redução ao rimeiro uadrante rimeiro Ano do Ensino Médio Autor: rof. Fabrício Siqueira enevides Revisor: rof. Antonio Caminha M.
54 CAPÍTULO 2. GEOMETRIA ANALÍTICA ( ) =
 54 CAPÍTULO. GEOMETRIA ANALÍTICA.5 Cônicas O grá co da equação + + + + + = 0 (.4) onde,,,, e são constantes com, e, não todos nulos, é uma cônica. A equação (.4) é chamada de equação geral do grau em e
54 CAPÍTULO. GEOMETRIA ANALÍTICA.5 Cônicas O grá co da equação + + + + + = 0 (.4) onde,,,, e são constantes com, e, não todos nulos, é uma cônica. A equação (.4) é chamada de equação geral do grau em e
Aula 19 Elipse - continuação
 MÓDULO 1 - AULA 19 Aula 19 Elipse - continuação Objetivos Desenhar a elipse com compasso e régua com escala. Determinar a equação reduzida da elipse no sistema de coordenadas com origem no ponto médio
MÓDULO 1 - AULA 19 Aula 19 Elipse - continuação Objetivos Desenhar a elipse com compasso e régua com escala. Determinar a equação reduzida da elipse no sistema de coordenadas com origem no ponto médio
Aula 12. Ângulo entre duas retas no espaço. Definição 1. O ângulo (r1, r2 ) entre duas retas r1 e r2 se define da seguinte maneira:
 Aula 1 1. Ângulo entre duas retas no espaço Definição 1 O ângulo (r1, r ) entre duas retas r1 e r se define da seguinte maneira: (r1, r ) 0o se r1 e r são coincidentes, Se as retas são concorrentes, isto
Aula 1 1. Ângulo entre duas retas no espaço Definição 1 O ângulo (r1, r ) entre duas retas r1 e r se define da seguinte maneira: (r1, r ) 0o se r1 e r são coincidentes, Se as retas são concorrentes, isto
Cálculo I IM UFRJ Lista 1: Pré-Cálculo Prof. Marco Cabral Versão Para o Aluno. Tópicos do Pré-Cálculo
 Cálculo I IM UFRJ Lista : Pré-Cálculo Prof. Marco Cabral Versão 7.03.05 Para o Aluno O sucesso (ou insucesso) no Cálculo depende do conhecimento de tópicos do ensino médio que chamaremos de pré-cálculo.
Cálculo I IM UFRJ Lista : Pré-Cálculo Prof. Marco Cabral Versão 7.03.05 Para o Aluno O sucesso (ou insucesso) no Cálculo depende do conhecimento de tópicos do ensino médio que chamaremos de pré-cálculo.
CÁLCULO I. 1 Número Reais. Objetivos da Aula
 CÁLCULO I Prof. Edilson Neri Júnior Prof. André Almeida EMENTA: Conceitos introdutórios de limite, limites trigonométricos, funções contínuas, derivada e aplicações. Noções introdutórias sobre a integral
CÁLCULO I Prof. Edilson Neri Júnior Prof. André Almeida EMENTA: Conceitos introdutórios de limite, limites trigonométricos, funções contínuas, derivada e aplicações. Noções introdutórias sobre a integral
PROPOSTA DE RESOLUÇÃO DA PROVA DE MATEMÁTICA A DO ENSINO SECUNDÁRIO (CÓDIGO DA PROVA 635) 2ª FASE 20 DE JULHO 2018 CADERNO 1
 Associação de Professores de Matemática Contactos: Rua Dr. João Couto, n.º 7-A 500-36 Lisboa Tel.: +35 76 36 90 / 7 03 77 Fax: +35 76 64 4 http://www.apm.pt email: geral@apm.pt PROPOSTA DE RESOLUÇÃO DA
Associação de Professores de Matemática Contactos: Rua Dr. João Couto, n.º 7-A 500-36 Lisboa Tel.: +35 76 36 90 / 7 03 77 Fax: +35 76 64 4 http://www.apm.pt email: geral@apm.pt PROPOSTA DE RESOLUÇÃO DA
1. Encontre as equações simétricas e paramétricas da reta que:
 Universidade Federal de Uberlândia Faculdade de Matemática Disciplina : Geometria Analítica (GMA00) Assunto: retas; planos; interseções de retas e planos; posições relativas entre retas e planos; distância
Universidade Federal de Uberlândia Faculdade de Matemática Disciplina : Geometria Analítica (GMA00) Assunto: retas; planos; interseções de retas e planos; posições relativas entre retas e planos; distância
Aula 5 Equações paramétricas de retas e planos
 Aula 5 Equações paramétricas de retas e planos MÓDULO 1 - AULA 5 Objetivo Estabelecer as equações paramétricas de retas e planos no espaço usando dados diversos. Na Aula 3, do Módulo 1, vimos como determinar
Aula 5 Equações paramétricas de retas e planos MÓDULO 1 - AULA 5 Objetivo Estabelecer as equações paramétricas de retas e planos no espaço usando dados diversos. Na Aula 3, do Módulo 1, vimos como determinar
UFRJ - Instituto de Matemática
 UFRJ - Instituto de Matemática Programa de Pós-Graduação em Ensino de Matemática www.pg.im.ufrj.br/pemat Mestrado em Ensino de Matemática Seleção 9 Etapa Questão. Determine se as afirmações abaio são verdadeiras
UFRJ - Instituto de Matemática Programa de Pós-Graduação em Ensino de Matemática www.pg.im.ufrj.br/pemat Mestrado em Ensino de Matemática Seleção 9 Etapa Questão. Determine se as afirmações abaio são verdadeiras
MÓDULO 1 - AULA 21. Objetivos
 Aula 1 Hipérbole - continuação Objetivos Aprender a desenhar a hipérbole com compasso e régua com escala. Determinar a equação reduzida da hipérbole no sistema de coordenadas com origem no ponto médio
Aula 1 Hipérbole - continuação Objetivos Aprender a desenhar a hipérbole com compasso e régua com escala. Determinar a equação reduzida da hipérbole no sistema de coordenadas com origem no ponto médio
Geometria Analítica I
 Geom. Analítica I Respostas do Módulo I - Aula 7 1 Geometria Analítica I 01/03/2011 Respostas dos Exercícios do Módulo I - Aula 7 Aula 7 1. a. Procedendo como nos Exemplos 7.1 e 7.2, ou a Proposição 7.15
Geom. Analítica I Respostas do Módulo I - Aula 7 1 Geometria Analítica I 01/03/2011 Respostas dos Exercícios do Módulo I - Aula 7 Aula 7 1. a. Procedendo como nos Exemplos 7.1 e 7.2, ou a Proposição 7.15
A primeira coisa a fazer é saber quais são as equações das curvas quando elas já se encontram na melhor
 Identificação de Cônicas Uma equação do segundo grau ax + bxy + cy + dx + ey + f = 0 define de maneira implícita uma curva no plano xy: o conjunto dos pontos (x, y) que satisfazem a equação. Por exemplo,
Identificação de Cônicas Uma equação do segundo grau ax + bxy + cy + dx + ey + f = 0 define de maneira implícita uma curva no plano xy: o conjunto dos pontos (x, y) que satisfazem a equação. Por exemplo,
Aula 11 Coordenadas polares
 MÓDULO 1 - AULA 11 Aula 11 Coordenadas polares Objetivos Definir as coordenadas polares no plano. Deduzir as relações de mudança de coordenadas polares para coordenadas cartesianas e vice-versa. Obter
MÓDULO 1 - AULA 11 Aula 11 Coordenadas polares Objetivos Definir as coordenadas polares no plano. Deduzir as relações de mudança de coordenadas polares para coordenadas cartesianas e vice-versa. Obter
Ana Carolina Boero. Página: Sala Bloco A - Campus Santo André
 Funções de uma variável real a valores reais E-mail: ana.boero@ufabc.edu.br Página: http://professor.ufabc.edu.br/~ana.boero Sala 512-2 - Bloco A - Campus Santo André Funções de uma variável real a valores
Funções de uma variável real a valores reais E-mail: ana.boero@ufabc.edu.br Página: http://professor.ufabc.edu.br/~ana.boero Sala 512-2 - Bloco A - Campus Santo André Funções de uma variável real a valores
Nome do aluno: N.º: Para responder aos itens de escolha múltipla, não apresente cálculos nem justificações e escreva, na folha de respostas:
 Teste de Matemática A 2017 / 2018 Teste N.º 2 Matemática A Duração do Teste (Caderno 1+ Caderno 2): 90 minutos 11.º Ano de Escolaridade Nome do aluno: N.º: Turma: Este teste é constituído por dois cadernos:
Teste de Matemática A 2017 / 2018 Teste N.º 2 Matemática A Duração do Teste (Caderno 1+ Caderno 2): 90 minutos 11.º Ano de Escolaridade Nome do aluno: N.º: Turma: Este teste é constituído por dois cadernos:
(a) Determine a velocidade do barco em qualquer instante.
 NOME: UNIVERSIDADE FEDERAL DO RIO DE JANEIRO Instituto de Matemática PRIMEIRA PROVA UNIFICADA CÁLCULO II Politécnica, Engenharia Química - 10/10/2013. 1 a QUESTÃO : Um barco a vela de massa m = 1 parte
NOME: UNIVERSIDADE FEDERAL DO RIO DE JANEIRO Instituto de Matemática PRIMEIRA PROVA UNIFICADA CÁLCULO II Politécnica, Engenharia Química - 10/10/2013. 1 a QUESTÃO : Um barco a vela de massa m = 1 parte
Geometria Analítica e Vetorial - Daniel Miranda, Rafael Grisi, Sinuê Lodovici
 Geometria Analítica e Vetorial - Daniel Miranda, Rafael Grisi, Sinuê Lodovici 5 Â N G U LO S E D I ST Â N C I A 5.1 ângulos No capítulo anterior nos concentramos no estudo da posição relativa entre dois
Geometria Analítica e Vetorial - Daniel Miranda, Rafael Grisi, Sinuê Lodovici 5 Â N G U LO S E D I ST Â N C I A 5.1 ângulos No capítulo anterior nos concentramos no estudo da posição relativa entre dois
1 Geometria Analítica Plana
 UNIVERSIDADE ESTADUAL DO PARANÁ CAMPUS DE CAMPO MOURÃO Curso: Matemática, 1º ano Disciplina: Geometria Analítica e Álgebra Linear Professora: Gislaine Aparecida Periçaro 1 Geometria Analítica Plana A Geometria
UNIVERSIDADE ESTADUAL DO PARANÁ CAMPUS DE CAMPO MOURÃO Curso: Matemática, 1º ano Disciplina: Geometria Analítica e Álgebra Linear Professora: Gislaine Aparecida Periçaro 1 Geometria Analítica Plana A Geometria
PROPOSTA DE RESOLUÇÃO DA PROVA DE MATEMÁTICA A DO ENSINO SECUNDÁRIO (CÓDIGO DA PROVA 635) 1ª FASE 25 DE JUNHO 2019 CADERNO 1. e AV.
 Associação de Professores de Matemática Contactos: Rua Dr. João Couto, n.º 7-A 1500-6 Lisboa Tel.: +51 1 716 6 90 / 1 711 0 77 Fa: +51 1 716 64 4 http://www.apm.pt email: geral@apm.pt PROPOSTA DE RESOLUÇÃO
Associação de Professores de Matemática Contactos: Rua Dr. João Couto, n.º 7-A 1500-6 Lisboa Tel.: +51 1 716 6 90 / 1 711 0 77 Fa: +51 1 716 64 4 http://www.apm.pt email: geral@apm.pt PROPOSTA DE RESOLUÇÃO
Aula 15. Derivadas Direcionais e Vetor Gradiente. Quando u = (1, 0) ou u = (0, 1), obtemos as derivadas parciais em relação a x ou y, respectivamente.
 Aula 15 Derivadas Direcionais e Vetor Gradiente Seja f(x, y) uma função de variáveis. Iremos usar a notação D u f(x 0, y 0 ) para: Derivada direcional de f no ponto (x 0, y 0 ), na direção do vetor unitário
Aula 15 Derivadas Direcionais e Vetor Gradiente Seja f(x, y) uma função de variáveis. Iremos usar a notação D u f(x 0, y 0 ) para: Derivada direcional de f no ponto (x 0, y 0 ), na direção do vetor unitário
1 Vetores no Plano e no Espaço
 1 Vetores no Plano e no Espaço Definimos as componentes de um vetor no espaço de forma análoga a que fizemos com vetores no plano. Vamos inicialmente introduzir um sistema de coordenadas retangulares no
1 Vetores no Plano e no Espaço Definimos as componentes de um vetor no espaço de forma análoga a que fizemos com vetores no plano. Vamos inicialmente introduzir um sistema de coordenadas retangulares no
Aula 31 Funções vetoriais de uma variável real
 MÓDULO 3 - AULA 31 Aula 31 Funções vetoriais de uma variável real Objetivos Conhecer as definições básicas de funções vetoriais de uma variável real. Aprender a parametrizar curvas simples. Introdução
MÓDULO 3 - AULA 31 Aula 31 Funções vetoriais de uma variável real Objetivos Conhecer as definições básicas de funções vetoriais de uma variável real. Aprender a parametrizar curvas simples. Introdução
Material Teórico - Módulo: Vetores em R 2 e R 3. Módulo e Produto Escalar - Parte 1. Terceiro Ano - Médio
 Material Teórico - Módulo: Vetores em R 2 e R 3 Módulo e Produto Escalar - Parte 1 Terceiro Ano - Médio Autor: Prof. Angelo Papa Neto Revisor: Prof. Antonio Caminha M. Neto 1 Módulo de um vetor O módulo
Material Teórico - Módulo: Vetores em R 2 e R 3 Módulo e Produto Escalar - Parte 1 Terceiro Ano - Médio Autor: Prof. Angelo Papa Neto Revisor: Prof. Antonio Caminha M. Neto 1 Módulo de um vetor O módulo
1 Segmentos orientados e vetores, adição e multiplicação
 MAP2110 Modelagem e Matemática 1 o Semestre de 2007 Resumo 1 - Roteiro de estudos - 07/05/2007 Espaços vetoriais bi e tri-dimensionais (plano ou espaço bidimensional E 2, e espaço tridimensional E 3 )
MAP2110 Modelagem e Matemática 1 o Semestre de 2007 Resumo 1 - Roteiro de estudos - 07/05/2007 Espaços vetoriais bi e tri-dimensionais (plano ou espaço bidimensional E 2, e espaço tridimensional E 3 )
Universidade Federal de Mato Grosso do Sul - UFMS VGA - 2 a Prova - Engenharia Civil + Física 03 de Julho de Prof o. E.T.
 Universidade Federal de Mato Grosso do Sul - UFMS VGA - 2 a Prova - Engenharia Civil + Física 0 de Julho de 2014 - Prof o ETGalante 1 (2,0 pontos) Na gura acima ABCDEF GH é um paralelepípedo O ponto M
Universidade Federal de Mato Grosso do Sul - UFMS VGA - 2 a Prova - Engenharia Civil + Física 0 de Julho de 2014 - Prof o ETGalante 1 (2,0 pontos) Na gura acima ABCDEF GH é um paralelepípedo O ponto M
Material de Apoio. Roteiro para Esboçar uma Curva 1
 Universidade Federal Rural de Pernambuco Departamento de Matemática Disciplina: Cálculo M I Prof a Yane Lísle Material de Apoio Roteiro para Esboçar uma Curva A lista a seguir pretende servir como um guia
Universidade Federal Rural de Pernambuco Departamento de Matemática Disciplina: Cálculo M I Prof a Yane Lísle Material de Apoio Roteiro para Esboçar uma Curva A lista a seguir pretende servir como um guia
f, da, onde R é uma das regiões mostradas na
 Integrais Duplas em Coordenadas Polares Bibliografia básica: THOMAS, G. B. Cálculo. Vol. Capítulo 1. Item 1.3. STEWAT, J. Cálculo. Vol.. Capítulo 15. Item 15.4. Sabemos que o cálculo da área de uma região
Integrais Duplas em Coordenadas Polares Bibliografia básica: THOMAS, G. B. Cálculo. Vol. Capítulo 1. Item 1.3. STEWAT, J. Cálculo. Vol.. Capítulo 15. Item 15.4. Sabemos que o cálculo da área de uma região
MAT2457 ÁLGEBRA LINEAR PARA ENGENHARIA I Gabarito da 2 a Prova - 1 o semestre de 2015
 MAT27 ÁLGEBRA LINEAR PARA ENGENHARIA I Gabarito da 2 a Prova - 1 o semestre de 201 Nesta prova considera-se fixada uma orientação do espaço e um sistema de coordenadas Σ (O, E) em E 3, em que E é uma base
MAT27 ÁLGEBRA LINEAR PARA ENGENHARIA I Gabarito da 2 a Prova - 1 o semestre de 201 Nesta prova considera-se fixada uma orientação do espaço e um sistema de coordenadas Σ (O, E) em E 3, em que E é uma base
Estado duplo ou, Estado plano de tensões.
 Estado duplo ou, Estado plano de tensões. tensão que atua em um ponto é função do plano pelo qual se faz o estudo. Esta afirmação pode ficar mais clara quando analisa, por exemplo, um ponto de uma barra
Estado duplo ou, Estado plano de tensões. tensão que atua em um ponto é função do plano pelo qual se faz o estudo. Esta afirmação pode ficar mais clara quando analisa, por exemplo, um ponto de uma barra
