Todos os exercícios sugeridos nesta apostila se referem ao volume 3. MATEMÁTICA III 1 ESTUDO DA CIRCUNFERÊNCIA
|
|
|
- Geraldo Frade Padilha
- 7 Há anos
- Visualizações:
Transcrição
1 DEFINIÇÃO... EQUAÇÃO REDUZIDA... EQUAÇÃO GERAL DA CIRCUNFERÊNCIA... 3 RECONHECIMENTO... 3 POSIÇÃO RELATIVA ENTRE PONTO E CIRCUNFERÊNCIA... 1 POSIÇÃO RELATIVA ENTRE RETA E CIRCUNFERÊNCIA PROBLEMAS DE TANGENCIA... 0 POSIÇÃO RELATIVA ENTRE DUAS CIRCUNFERÊNCIAS... 3 RESPOSTAS... 8 REFERÊNCIA BIBLIOGRÁFICA No final das séries de exercícios podem aparecer sugestões de atividades complementares. Estas sugestões referem-se a exercícios do livro Matemática de Manoel Paiva fornecido pelo FNDE e adotado pelo IFMG Campus Ouro Preto durante o triênio Todos os exercícios sugeridos nesta apostila se referem ao volume 3. MATEMÁTICA III 1 ESTUDO DA CIRCUNFERÊNCIA
2 DEFINIÇÃO Circunferência é um conjunto de pontos do plano eqüidistantes de um ponto fixo chamado CENTRO. A distância do centro a qualquer ponto da circunferência é denominada RAIO. Uma circunferência está bem determinada quando são conhecidos seu centro e raio. Consideremos a circunferência de centro no ponto C(a, b) e raio r como na figura abaixo: Como D x a y b PC, desta forma, podemos escrever que: x a y b r ou x a y b r Ex.1: Escrever a equação da circunferência de centro no ponto (5, 3) e raio 7. Resolução: Substituindo a, b e r na expressão x a y b r, temos que a equação procurada é x 5 y Um ponto P(x, y) pertence a se, e somente se, a distância PC é igual ao raio r. P D r PC EQUAÇÃO REDUZIDA Chama-se equação da circunferência aquela que é satisfeita por todo ponto P(x, y) pertencente à curva. Como foi destacado acima, P se verificar a condição DPC r, assim, temos que: P D r PC Ex.: Qual a equação da circunferência de centro na origem e raio 4? Resolução: A partir do enunciado, temos a = 0, b = 0 e r = 4 e, substituindo na expressão dada, encontramos x y 16. Em sentido contrário, quando encontramos uma equação na forma x a y b r com r 0 já podemos afirmar que descreve uma circunferência de centro em C(a, b) e raio r. CÁSSIO VIDIGAL IFMG CAMPUS OURO PRETO
3 Ex.1: Identificar o centro e o raio da circunferência de equação x y 4 5. Resolução: Comparando a equação dada com aquela apresentada acima, temos que a =, b = -4 e r = 5, logo o centro é o ponto C(, -4) e raio 5. Ex.: Qual o centro e o raio da circunferência que é apresentada pela equação x Resolução: y 4 13? Podemos reescrever a equação por x y , assim, o centro é o ponto C(0, 4) e o raio é 13. EQUAÇÃO GERAL DA CIRCUNFERÊNCIA O desenvolvimento da equação reduzida, nos leva à equação geral da circunferência, acompanhe: x a y b r x ax a y by b r 0 x y ax by a b r 0 x y ax by k 0 k Ex.: Escrever a equação geral da circunferência de centro no ponto C(1, -3) e raio 4. Resolução: k a b r x y ax by k 0 x y x y x y x y RECONHECIMENTO É essencial saber reconhecer quando uma equação do º grau, dada em termos de x e y, representa uma circunferência. Vamos partir da equação Ax By Cxy Dx Ey F 0 que, a partir de agora, trataremos por E1. Dividindo todos os termos de E1 por A, obtemos a equação abaixo que denominaremos E: B C D E F x y xy x y 0 A A A A A Vamos agora comparar E, termo a termo, com a equação geral apresentada na página anterior: x y ax by k 0 B C D E F 0 A A A A A x y xy x y Podemos concluir que: MATEMÁTICA III 3 ESTUDO DA CIRCUNFERÊNCIA
4 1. B 1 A B 0 A. C 0 C 0 A 3. D D a a A A 4. E E b b A A 5. F F k a b r A A F D E r A A A D E F r r 4A 4A A D E 4AF 4A como r é um número real positivo, então r 0, então: D E 4AF 0 4A E, resumindo, são três as condições para que E1 represente uma circunferência: I. AB 0 II. C 0 III. D E 4AF 0 4A Satisfeitas estas três condições, temos que a equação Ax By Cxy Dx Ey F 0 representa uma circunferência de centro D E C, A A e raio D E 4AF. A OBSERVAÇÔES a. Se uma das três condições citadas acima não for satisfeita, a equação representa um lugar geométrico diferente de uma circunferência ou até mesmo um conjunto vazio. b. Quando a equação da circunferência apresenta coeficientes unitários para x e y, (A = B = 1), o centro e o raio da circunferência podem ser encontrados a partir de: D E a, b e r a b k c. Se os coeficientes de x e y não forem unitários, podemos dividir todos os coeficientes da equação da circunferência por A, assim obteremos uma equação onde tais coeficientes serão iguais a 1. d. Outro processo rápido de encontrar o centro e o raio de uma circunferência, consiste em escrever a equação na forma reduzida x a y b r e, por uma comparação simples, extraímos as informações que caracterizam centro e raio. Ex.1: Dentre as equações a seguir, destaque aquelas que representam e aquelas que não representam uma circunferência e justifique aquelas que não representam: A x 3y 5x 7y 1 0 B C D E x y xy x y x 3y 4x 6y 15 0 x y x y 0 x y 4x 6y 3 0 CÁSSIO VIDIGAL 4 IFMG CAMPUS OURO PRETO
5 Resolução: A não representa uma circunferência pois os coeficientes de x e y são diferentes. B não representa uma circunferência pois o coeficiente de xy é diferente de zero. C não representa uma circunferência pois D E 4AF D não representa uma circunferência pois D E 4AF Desta forma, o raio seria nulo. E representa uma circunferência pois A B 0, C 0 pelo fato de não aparecer o termo xy e, por fim, D E AF Ex.: Achar o centro e o raio da circunferência de equação x y 6x 4y Resolução: Este problema pode ser resolvido por métodos diferentes. Vamos destacar dois destes métodos: Método 1 Uma das formas de encontrar as coordenadas do centro e o raio consiste em completar os quadrados e escrever a equação na forma reduzida extraindo, daí, as informações pedidas, acompanhe na próxima página: x y x y x x y y x x y y x x y y x x y y x y Na linha isolamos o termo independente. Na linha 3 criamos os espaços que usaremos para de completar os quadrados. Na linha 4 foram completados os quadrados dividindo os coeficientes de x e y por e elevando o resultado ao quadrado. Estes valores foram somados em ambos os membros da equação. Na linha 5 destacamos, entre parênteses os dois trinômios quadrados perfeitos obtidos. Por fim, na linha 6 fatoramos os dois trinômios com o objetivo de obter uma forma reduzida da equação da circunferência. Daí, podemos afirmar que a circunferência dada tem centro no ponto C(3, -) e raio 5. Método Vamos comparar a equação dada com uma equação geral de circunferência com coeficientes de x e y iguais a 1, acompanhe; x y x y x y ax by k 0 Comparando termo a termo as duas equações, temos que: 3 MATEMÁTICA III 5 ESTUDO DA CIRCUNFERÊNCIA
6 a 6 a 3 b 4 b k 13 k a b r 13 a b r 13 3 r r r 5 r 5 Daí, mais uma vez, concluímos que a circunferência dada tem centro no ponto C(3, -) e raio 5. OBSERVAÇÃO: Por mais que esta segunda resolução pareça mais fácil e mais rápida, devemos considerar que este método demanda decorar uma fórmula. De qualquer forma, ficam as duas opções. Ex.3: Obter centro e raio da circunferência descrita por 4x 4y 4x 1y x 4y 4x 1y x y x 3y 0 3 x x y 3y x x y 3y x x y 3y x x y 3y 1 3 x y 1 Assim, podemos afirmar que a 1 3 circunferência tem centro em C, e raio 1. OBSERVAÇÃO: assim como no exemplo anterior, este também pode ser resolvido de duas maneiras distintas tomando o cuidado, entretanto, para o fato de os coeficientes de x e y serem diferentes de 1. Neste caso, ainda é recomendável simplificar a equação. Resolução: Vamos resolver tal como fizemos no primeiro método do exemplo anterior porém vamos, antes, dividir toda a equação por 4 a fim de tornar os coeficientes de x e y iguais a 1. CÁSSIO VIDIGAL 6 IFMG CAMPUS OURO PRETO
7 01) Determinar a equação da circunferência de centro e raio indicados em cada item: C 0, 0 e r 3 a) d) C, 4 e r 1 b) C, 0 e r 4 e) C 0, 3 e r c) C 1, e r 5 f) 1 3 C, e r 4 MATEMÁTICA III 7 ESTUDO DA CIRCUNFERÊNCIA
8 0) Qual a equação da circunferência que passa pelo ponto P(5, 5) e tem centro no ponto C(1, )? b) x y x ) Determinar o centro e o raio de cada uma das circunferências apresentadas a seguir: a) x y 6x 4y 1 0 c) x y y x CÁSSIO VIDIGAL 8 IFMG CAMPUS OURO PRETO
9 d) x y 8x 6y 0 04) Achar a equação da reta que passa pelo centro da circunferência x y 3 8 e é perpendicular à reta r : x y e) 3x 3y 6x 1y 14 0 MATEMÁTICA III 9 ESTUDO DA CIRCUNFERÊNCIA
10 05) Determinar o centro e o raio da circunferência de equação 4x 4y 1x 1y ) Um quadrado tem vértices consecutivos nos pontos A(5, 0) e B(-1, 0). Escreva a equação da circunferência circunscrita a este quadrado. 06) Dada a circunferência de equação x y mx ny p 0, determine a relação entre m, n e p a fim de que a circunferência tangencie os eixos. CÁSSIO VIDIGAL 10 IFMG CAMPUS OURO PRETO
11 08) Qual a equação da circunferência que passa pelos pontos A(, 4), B(11, 7) e D(7, 9). 09) O ponto P(3, b) pertence à circunferência de centro em C(0, 3) e raio 5. Calcule o valor da coordenada b. 10) Qual o comprimento do lado do triângulo eqüilátero inscrito na circunferência x y x 10y 10 0? ATIVIDADES COMPLEMENTARES Pág. 90 Exercícios R1 a R5 Pág.95 Exercícios 11 a 17 MATEMÁTICA III 11 ESTUDO DA CIRCUNFERÊNCIA
12 POSIÇÃO RELATIVA ENTRE PONTO E CIRCUNFERÊNCIA º caso: P pertence a. Dados um ponto P(x0, y0) e uma circunferência : x a y b r, vamos determinar a posição relativa entre P e. Vamos calcular a distância de P até C e comparar com o raio e, assim, temos três casos: 1º caso: P é exterior a. Isso ocorre se, e somente se: D PC = r (x 0 a) + (y 0 b) = r (x 0 a) + (y 0 b) r = 0 3º caso: P pertence a. Isso ocorre se, e somente se: D PC > r Isto é (x 0 a) + (y 0 b) > r Ou, anda melhor: (x 0 a) + (y 0 b) r > 0 Isso ocorre se, e somente se: D PC < r (x 0 a) + (y 0 b) < r (x 0 a) + (y 0 b) r < 0 CÁSSIO VIDIGAL 1 IFMG CAMPUS OURO PRETO
13 Podemos resumir esta teoria com a seguinte ideia: dada a circunferência : x y ax by k 0 onde k a b r primeiro membro, isto é: f x, y x y ax by a b r, seja f(x, y) o polinômio do Quando é dado P(x0, y0), cuja posição em relação a queremos determinar, substituímos (x0, y0) em f, ou seja, calculamos f x, y x y ax by a b r então, conforme acabamos de estudar, 0 0 f x, y 0 P é exterior a. f x, y 0 P pertence a f x, y 0 P é interior a. P 0, Como P 0,0 0, P pertence a. Ex.3: Qual a posição do ponto P(0, 1) em relação à circunferência : x y 5x y 11 0? Resolução: A partir de P x, y x y 5x y 11, vamos fazer P 0,1. P 0, Como P 0,1 8, P é interior a. Ex.1: Qual a posição do ponto P(, 3) em relação à circunferência : x y 4x 0? Resolução: Temos P x, y x y 4x então, P, OBSERVAÇÃO: Note que substituir P(x0, y0) na função f(x, y) é muito mais simples do que calcular a distância PC e comparar com o raio uma vez que obter C e r é uma operação trabalhosa principalmente se a equação da circunferência apresentar coeficientes fracionários ou irracionais. Como P,3 0, P é exterior a. Ex.: Qual a posição do ponto P(0, 0) em relação à circunferência : x y 3x y 0? Resolução: Sendo P x, y x y 3x y, vamos fazer P 0,0. MATEMÁTICA III 13 ESTUDO DA CIRCUNFERÊNCIA
14 11) Determinar a posição do ponto P em relação à circunferência l em cada item abaixo: a) P(, 1) e : x y 9 0 1) Determinar P de modo que o ponto A(7, 9) seja exterior à circunferência x y x y p 0. (A resolução desta questão pode ser encontrada na seção RESPOSTAS) b) P(-4, -5) e : x y x y 0 13) Interprete graficamente a solução de cada uma das inequações do º grau a seguir: a) x y 9 c) P(0, 0) e : x y 3x y 1 0 CÁSSIO VIDIGAL 14 IFMG CAMPUS OURO PRETO
15 b) x y 4 d) x y x y 1 0 c) x y x y ) Resolver o sistema x y x y (A resolução desta questão pode ser encontrada na secção RESPOSTAS) 9 4 MATEMÁTICA III 15 ESTUDO DA CIRCUNFERÊNCIA
16 15) Resolva o sistema de inequações x y 9 x y 3 encontrada na seção RESPOSTAS). (A resolução desta questão pode ser 16) Resolver os seguintes sistemas de inequações do segundo grau: x y 9 a) x y 1 x y 4 b) x 1 y 4 CÁSSIO VIDIGAL 16 IFMG CAMPUS OURO PRETO
17 c) x y 5 x y x POSIÇÃO RELATIVA ENTRE RETA E CIRCUNFERÊNCIA Seja uma circunferência de centro no ponto C(a, b) e raio r. Existem, no plano, retas que cortam a circunferência em dois pontos, retas que tocam a circunferência em um único ponto e retas que não interceptam em ponto algum. Estas retas são chamadas, respectivamente, de SECANTES, TANGENTES e EXTERNAS À CIRCUNFERÊNCIA. Observe a figura: d) x y x y 1 1 e e é exterior à circunferência t T t é tangente à circunferência s S, S 1 s é secante à circunferência Considerando a circunferência : x y ax by k 0 e a reta dada por r : Ax By C 0, a solução do sistema a seguir determina a posição da reta r em relação à circunferência. MATEMÁTICA III 17 ESTUDO DA CIRCUNFERÊNCIA
18 S : Ax By C 0 : x y ax by k 0 Se S tem duas soluções distintas, r é secante à. Se S tem solução única, r é tangente à. Se S não admite soluções reais, então r é exterior à circunferência. Utilize a figura da segunda coluna da página anterior para interpretar estas informações. Na apostila anterior, aprendemos a calcular a distância entre ponto e reta. 17) Calcular a distância do centro da circunferência x y 5x 7y 1 0 e a reta 4x 3y 0. Ex.: Qual a posição relativa entre a circunferência x y reta 3x y 0? Resolução: e a Devemos resolver o sistema x 3 y xy 0 Resolvendo-o, encontramos como solução os pares ordenados (0, 0) e (3, 9). Como o sistema admite duas soluções distintas, concluímos que a reta é secante à circunferência. OBSERVAÇÃO Existe um método alternativo de determinar a posição relativa entre uma circunferência e uma reta. Este método consiste em encontrar a distância entre o centro da circunferência e a reta e, em seguida comparar esta distância com o raio, assim: d r s é sec ante a Cs d r t é tangente a Ct d r e é exterior a Ce CÁSSIO VIDIGAL 18 IFMG CAMPUS OURO PRETO
19 18) Qual a posição relativa entre a reta r : 4x 3y 0 e a circunferência x y x y ? 0) Determinar os pontos P e Q onde a circunferência x y 4x 6y 0 encontra a reta 3x + y + 1 = 0. 19) Qual a posição do eixo das abscissas em relação à circunferência x y 5x 4y ) Quais as equações das retas paralelas ao eixo das abscissas tangentes à circunferência x y 1 9? MATEMÁTICA III 19 ESTUDO DA CIRCUNFERÊNCIA
20 ) Qual o comprimento da corda que a reta 7x 4y 4 = 0 determina na circunferência x y x 6y 15 0? PROBLEMAS DE TANGENCIA Vamos ver, por meio de exemplos, dois problemas clássicos de tangencia entre reta e circunferência. 1º problema: Determinar duas retas com inclinação dada e tangentes à uma circunferência. Ex.: Determinar as retas tangentes à circunferência x y 4x y 4 0 que formam um ângulo de 45º com o eixo Ox. Resolução Em princípio, vamos determinar o centro e o raio da circunferência: 3) Escrever a equação da circunferência de centro no ponto (5, 4) e tangente à reta 3x 3y + 14 = 0. 4 a e b 1 r a b k Como as tangentes formam 45 com o eixo horizontal, podemos afirmar que possuem m = 1. Além disso, distam 3 unidades do centro C(, 1). Temos então, que as retas tangentes possuem equação t : y x n ou t : x y n 0. Daí, CÁSSIO VIDIGAL 0 IFMG CAMPUS OURO PRETO
21 D Ct n 1 1 n 1 3 n 1 3 n Assim, as retas tangentes são: t : x y t : x y º problema: Determinar as equações das duas retas que passam por um ponto dado tangentes à uma circunferência. Ex.: Determinar as equações das retas tangentes à circunferência x y 1 4 traçadas a partir do ponto P(-5, -6). Resolução: Como a equação da circunferência foi apresentada na forma reduzida, podemos afirmar, sem maiores dificuldades, que seu centro é o ponto C(- 1, ) e o raio é. Observe a ilustração: Antes de tudo, devemos nos certificar que o problema tem solução, e isso acontece somente se P não for interior à circunferência. A ilustração acima nos mostra isso mas a solução gráfica não é suficiente, vamos, então, calcular a distância PC: D PC logo P é externo e o problema tem duas soluções que são as retas t da ilustração. De t, podemos dizer que: y 6 m... mx y 5m 6 0 x 5 Mas também sabemos que t dista unidades de C(-1, ), assim: m 1 5m 6 m 1 m 1 4m 8 4m 8 m 1 16m 64m 64 4m 4 1m 64m m 16m m 3 logo, as equações procuradas serão encontradas substituindo m 3 em mx y 5m 6 0 e, assim, t1 x y t x y MATEMÁTICA III 1 ESTUDO DA CIRCUNFERÊNCIA
22 4) Obter as equações das tangentes à circunferência x y 3 36 que sejam paralelas à reta 3x y ) Determine as equações das retas tangentes à circunferência x y 1 que passam pelo ponto P, 0. CÁSSIO VIDIGAL IFMG CAMPUS OURO PRETO
23 POSIÇÃO RELATIVA ENTRE DUAS CIRCUNFERÊNCIAS 3º caso: A posição relativa entre duas circunferências será determinada comparando a distância entre seus centros com a soma ou subtração do comprimento de seus raios. Veja os 6 casos: 1º caso: d r1 r pois d C P PC 1 r1 r d r1 r Circunferências tangentes interiormente pois d C P PP P C r r r1 r 4º caso: Circunferências exteriores º caso: r1 r d r1 r pois d r1 r pois d C P P C PP r r r 1 1 r 0 d C P PC r r r 0 d C P P C r r r1 r Circunferências secantes Circunferências tangentes exteriormente MATEMÁTICA III 3 ESTUDO DA CIRCUNFERÊNCIA
24 5º caso: Ex.: Qual a posição relativa entre as circunferências : x y 49 e 1 : x y 6x 8y 11 0? Resolução: 0 d r1 r pois Temos: 1 centro 0,0 1 centro CC 1 C e raio r1 7 C 3,4 e raio r 6 d d C P C P PP r r r1 r 0 Circunferência de menor raio é interior à outra Comparando a soma dos raios: CC e r 1 r 13 e daí concluímos 1 5 que 1 e não podem ser exteriores nem tangente exteriormente. 6º caso: Comparando a diferença dos raios: CC 1 5 e r1r 1 e, consequentemente 1 e não podem ser concêntricas, uma interior a outra nem tangentes interiormente. Por exclusão, 1 e secantes. são d 0 Circunferências concêntrias Você deve ter atenção pois este é o caso que exige mais cuidados pois são necessárias duas comparações: C1C r1 r e C1C r1 r. Nos demais casos, ao comparar CC 1 com r 1 r ou com r 1 r, já podemos tirar conclusões. CÁSSIO VIDIGAL 4 IFMG CAMPUS OURO PRETO
25 6) Qual a posição relativa entre 1 e em cada caso a seguir? a) : x y 36 e 1 : x y 6x 8y 1 0 b) : x y 4x 0 e 1 : x y x 3 0 MATEMÁTICA III 5 ESTUDO DA CIRCUNFERÊNCIA
26 c) : x y 8 0 e d) : x y 8x 6y 0 e 1 1 : x y 6x 6y 17 0 : x y x 0 CÁSSIO VIDIGAL 6 IFMG CAMPUS OURO PRETO
27 e) : x y 49 e 7) Obter a intersecção entre as 1 : x y 6x 8y 1 0 circunferências : x y 100 e 1 : x y 1 x 1 y MATEMÁTICA III 7 ESTUDO DA CIRCUNFERÊNCIA
28 RESPOSTAS 01) a) x y 9 b) x y 16 c) x y d) x y e) f) x y x y 1 0) x y ) a) C e r b) C 4, 0 e r 3 c) C e r 3, 5 3, d) C, e r e) C 1, e r 3 3 1) Resolução Fazendo f x, y x y x y p, devemos ter f 7, 9 0, assim, f f 7, p 7, 9 98 p 98 p 0 Portanto p 98. Por outro lado, uma condição para a existência da circunferência é que D E 4AF 0, e, assim, 4 4 4p 0 p Fazendo a intersecção entre as duas condições, temos a solução. Portanto: p 98 04) x + y 5 = 0 05) 06) C, e r m n 0e m 4p 13) a) 07) x y 08) 3 18 x y x y b) 09) 7 ou -1 10) ) a) exterior b) exterior c) interior c) d) CÁSSIO VIDIGAL 8 IFMG CAMPUS OURO PRETO
29 14) Resolução: Note que as duas inequações que formam o sistema são as mesmas dos itens a) e b) da questão anterior e a solução é a intersecção dos dois conjuntos, assim, a solução está apresentada abaixo: 16) a) b) Em outras palavras, a solução é uma coroa circular com uma unidade de largura. c) 15) A solução da primeira inequação, nós já conhecemos: d) Vamos agora destacar a solução da segunda inequação: 17) ) r é secante à circunferência. 19) O eixo Ox é secante à circunferência. 0) P(-4, 0) e Q(0, -6) Agora, fazendo a intersecção entre as duas soluções, encontramos o conjunto de pontos procurado, portando, a solução do sistema de inequações é 1) y = 5 ou y = -1 ) 8 3) x y ) 3x y ) x y 0 e x y 0 MATEMÁTICA III 9 ESTUDO DA CIRCUNFERÊNCIA
30 6) a) secantes b) concêntricas c) exteriores d) secantes e) Tangentes interiormente 7) (1, ) e (3, 4) REFERÊNCIA BIBLIOGRÁFICA DANTE, Luiz Roberto; Matemática, Volume dois. São Paulo, Atica, 005. IEZZI, Gelson e outros; Fundamentos da Matemática Elementar, Volume 4. São Paulo, Atual, 5ª edição, Links para os vídeos sugeridos: Pág ao-geral-da-circunferencia/ Pág ao-relativa-entre-ponto-e-circunferencia/ CÁSSIO VIDIGAL 30 IFMG CAMPUS OURO PRETO
Concluimos dai que o centro da circunferência é C = (6, 4) e o raio é
 QUESTÕES-AULA 17 1. A equação x 2 + y 2 12x + 8y + 0 = 0 representa uma circunferência de centro C = (a, b) e de raio R. Determinar o valor de a + b + R. Solução Completamos quadrados na expressão dada.
QUESTÕES-AULA 17 1. A equação x 2 + y 2 12x + 8y + 0 = 0 representa uma circunferência de centro C = (a, b) e de raio R. Determinar o valor de a + b + R. Solução Completamos quadrados na expressão dada.
Todos os exercícios sugeridos nesta apostila se referem ao volume 1. MATEMÁTICA I 1 FUNÇÃO QUADRÁTICA PARTE 2
 EIXO DE SIMETRIA... COEFICIENTES a, b E c NO GRÁFICO... SINAL DA FUNÇÃO QUADRÁTICA...4 INEQUAÇÕES DO º GRAU...9 INEQUAÇÕES PRODUTO E QUOCIENTE... 4 SISTEMA DE INEQUAÇÕES DO º GRAU... 8 REFERÊNCIA BIBLIOGRÁFICA...
EIXO DE SIMETRIA... COEFICIENTES a, b E c NO GRÁFICO... SINAL DA FUNÇÃO QUADRÁTICA...4 INEQUAÇÕES DO º GRAU...9 INEQUAÇÕES PRODUTO E QUOCIENTE... 4 SISTEMA DE INEQUAÇÕES DO º GRAU... 8 REFERÊNCIA BIBLIOGRÁFICA...
Todos os exercícios sugeridos nesta apostila se referem ao volume 3. MATEMÁTICA III 1 GEOMETRIA ANALÍTICA ESTUDO DA RETA
 EQUAÇÃO GERAL DA RETA... EQUAÇÃO REDUZIDA DA RETA... 8 EQUAÇÃO SEGMENTÁRIA DA RETA... 4 EQUAÇÃO PARAMÉTRICA... 5 POSIÇÕES RELATIVAS DE DUAS RETAS NO PLANO... 8 CONDIÇÃO DE PARALELISMO... 6 CONDIÇÃO DE
EQUAÇÃO GERAL DA RETA... EQUAÇÃO REDUZIDA DA RETA... 8 EQUAÇÃO SEGMENTÁRIA DA RETA... 4 EQUAÇÃO PARAMÉTRICA... 5 POSIÇÕES RELATIVAS DE DUAS RETAS NO PLANO... 8 CONDIÇÃO DE PARALELISMO... 6 CONDIÇÃO DE
Todos os exercícios sugeridos nesta apostila se referem ao volume 1.
 CONCEITO DE FUNÇÃO... 2 IMAGEM DE UMA FUNÇÃO... 8 IMAGEM A PARTIR DE UM GRÁFICO... 12 DOMÍNIO DE UMA FUNÇÃO... 15 DETERMIAÇÃO DO DOMÍNIO... 15 DOMÍNIO A PARTIR DE UM GRÁFICO... 17 GRÁFICO DE UMA FUNÇÃO...
CONCEITO DE FUNÇÃO... 2 IMAGEM DE UMA FUNÇÃO... 8 IMAGEM A PARTIR DE UM GRÁFICO... 12 DOMÍNIO DE UMA FUNÇÃO... 15 DETERMIAÇÃO DO DOMÍNIO... 15 DOMÍNIO A PARTIR DE UM GRÁFICO... 17 GRÁFICO DE UMA FUNÇÃO...
Estudante: Circunferência: Equação reduzida da circunferência: Circunferência: Consideremos uma circunferência de centro C (a, b) e raio r.
 Gênesis Soares Jaboatão, de de 014. Estudante: Circunferência: Circunferência: A circunferência é o conjunto de todos os pontos de plano equidistantes de outro ponto C do mesmo plano chamado centro da
Gênesis Soares Jaboatão, de de 014. Estudante: Circunferência: Circunferência: A circunferência é o conjunto de todos os pontos de plano equidistantes de outro ponto C do mesmo plano chamado centro da
Plano cartesiano, Retas e. Alex Oliveira. Circunferência
 Plano cartesiano, Retas e Alex Oliveira Circunferência Sistema cartesiano ortogonal O sistema cartesiano ortogonal é formado por dois eixos ortogonais(eixo x e eixo y). A intersecção dos eixos x e y é
Plano cartesiano, Retas e Alex Oliveira Circunferência Sistema cartesiano ortogonal O sistema cartesiano ortogonal é formado por dois eixos ortogonais(eixo x e eixo y). A intersecção dos eixos x e y é
GEOMETRIA ANALÍTICA. 2) Obtenha o ponto P do eixo das ordenadas que dista 10 unidades do ponto Q (6, -5).
 GEOMETRIA ANALÍTICA Distância entre Dois Pontos Sejam os pontos A(xA, ya) e B(xB, yb) e sendo d(a, B) a distância entre eles, temos: Aplicando o teorema de Pitágoras ao triângulo retângulo ABC, vem: [d
GEOMETRIA ANALÍTICA Distância entre Dois Pontos Sejam os pontos A(xA, ya) e B(xB, yb) e sendo d(a, B) a distância entre eles, temos: Aplicando o teorema de Pitágoras ao triângulo retângulo ABC, vem: [d
Matemática B Extensivo V. 7
 Matemática Etensivo V. 7 Eercícios ) D ) ) 6 Temos que: 6 e 6 Logo, C (, ) (, ). 6 Completando quadrado, temos: ( ) ( 6) ( ) ( 6 9) 9 ( ) ( ) 9 ( ) ( ) 6 ( ) ( ) 6 ( ) ( ) Logo, C (, ) e r. Portanto, (
Matemática Etensivo V. 7 Eercícios ) D ) ) 6 Temos que: 6 e 6 Logo, C (, ) (, ). 6 Completando quadrado, temos: ( ) ( 6) ( ) ( 6 9) 9 ( ) ( ) 9 ( ) ( ) 6 ( ) ( ) 6 ( ) ( ) Logo, C (, ) e r. Portanto, (
Todos os exercícios sugeridos nesta apostila se referem ao volume 1. MATEMÁTICA I 1 FUNÇÃO DO 1º GRAU
 FUNÇÃO IDENTIDADE... FUNÇÃO LINEAR... FUNÇÃO AFIM... 5 GRÁFICO DA FUNÇÃO DO º GRAU... 5 IMAGEM... COEFICIENTES DA FUNÇÃO AFIM... ZERO DA FUNÇÃO AFIM... 7 FUNÇÕES CRESCENTES OU DECRESCENTES... 7 SINAL DE
FUNÇÃO IDENTIDADE... FUNÇÃO LINEAR... FUNÇÃO AFIM... 5 GRÁFICO DA FUNÇÃO DO º GRAU... 5 IMAGEM... COEFICIENTES DA FUNÇÃO AFIM... ZERO DA FUNÇÃO AFIM... 7 FUNÇÕES CRESCENTES OU DECRESCENTES... 7 SINAL DE
3º. EM Prof a. Valéria Rojas Assunto: Determinante, Área do Triângulo, Equação da reta, Eq. Reduzida da Reta
 1 - O uso do Determinante de terceira ordem na Geometria Analítica 1.1 - Área de um triângulo Seja o triângulo ABC de vértices A(x a, y a ), B(x b, x c ) e C(x c, y c ). A área S desse triângulo é dada
1 - O uso do Determinante de terceira ordem na Geometria Analítica 1.1 - Área de um triângulo Seja o triângulo ABC de vértices A(x a, y a ), B(x b, x c ) e C(x c, y c ). A área S desse triângulo é dada
Posição relativa entre retas e círculos e distâncias
 4 Posição relativa entre retas e círculos e distâncias Sumário 4.1 Distância de um ponto a uma reta.......... 2 4.2 Posição relativa de uma reta e um círculo no plano 4 4.3 Distância entre duas retas no
4 Posição relativa entre retas e círculos e distâncias Sumário 4.1 Distância de um ponto a uma reta.......... 2 4.2 Posição relativa de uma reta e um círculo no plano 4 4.3 Distância entre duas retas no
Todos os exercícios sugeridos nesta apostila se referem ao volume 1. MATEMÁTICA I 1 RELAÇÕES e FUNÇÕES
 PAR ORDENADO... 2 PRODUTO CARTESIANO... 3 REPRESENTAÇÃO GRÁFICA... 4 RELAÇÃO... 8 DOMÍNIO E IMAGEM... 12 CONTRA-DOMÍNIO... 13 RELAÇÃO INVERSA... 17 PROPRIEDADES DA RELAÇÃO INVERSA... 18 FUNÇÕES... 22 IMAGEM
PAR ORDENADO... 2 PRODUTO CARTESIANO... 3 REPRESENTAÇÃO GRÁFICA... 4 RELAÇÃO... 8 DOMÍNIO E IMAGEM... 12 CONTRA-DOMÍNIO... 13 RELAÇÃO INVERSA... 17 PROPRIEDADES DA RELAÇÃO INVERSA... 18 FUNÇÕES... 22 IMAGEM
ALUNO(A): Prof.: André Luiz Acesse: 02/05/2012
 1. FUNÇÃO 1.1. DEFINIÇÃO Uma função é um conjunto de pares ordenados de números (x,y) no qual duas duplas ordenadas distintas não podem ter o mesmo primeiro número, ou seja, garante que y seja único para
1. FUNÇÃO 1.1. DEFINIÇÃO Uma função é um conjunto de pares ordenados de números (x,y) no qual duas duplas ordenadas distintas não podem ter o mesmo primeiro número, ou seja, garante que y seja único para
Geometria Analítica - Aula
 Geometria Analítica - Aula 19 246 IM-UFF K. Frensel - J. Delgado Aula 20 Vamos analisar a equação Ax 2 + Cy 2 + Dx + Ey + F = 0 nos casos em que exatamente um dos coeficientes A ou C é nulo. 1. Parábola
Geometria Analítica - Aula 19 246 IM-UFF K. Frensel - J. Delgado Aula 20 Vamos analisar a equação Ax 2 + Cy 2 + Dx + Ey + F = 0 nos casos em que exatamente um dos coeficientes A ou C é nulo. 1. Parábola
Todos os exercícios sugeridos nesta apostila se referem ao volume 1. MATEMÁTICA I 1 RELAÇÕES
 FUNÇÃO DEFINIDA POR MAIS DE UMA SENTENÇA... MÓDULO... 6 PROPRIEDADES DO MÓDULO... 6 FUNÇÃO MODULAR... 9 GRÁFICO DA FUNÇÃO MODULAR... 9 EQUAÇÕES MODULARES... 7 INEQUAÇÕES MODULARES... 3 RESPOSTAS... 37
FUNÇÃO DEFINIDA POR MAIS DE UMA SENTENÇA... MÓDULO... 6 PROPRIEDADES DO MÓDULO... 6 FUNÇÃO MODULAR... 9 GRÁFICO DA FUNÇÃO MODULAR... 9 EQUAÇÕES MODULARES... 7 INEQUAÇÕES MODULARES... 3 RESPOSTAS... 37
Todos os exercícios sugeridos nesta apostila se referem ao volume 1. MATEMÁTICA I 1 FUNÇÃO DO 1º GRAU
 FUNÇÃO IDENTIDADE... FUNÇÃO LINEAR... FUNÇÃO AFIM... GRÁFICO DA FUNÇÃO DO º GRAU... IMAGEM... COEFICIENTES DA FUNÇÃO AFIM... ZERO DA FUNÇÃO AFIM... 6 FUNÇÕES CRESCENTES OU DECRESCENTES... 7 SINAL DE UMA
FUNÇÃO IDENTIDADE... FUNÇÃO LINEAR... FUNÇÃO AFIM... GRÁFICO DA FUNÇÃO DO º GRAU... IMAGEM... COEFICIENTES DA FUNÇÃO AFIM... ZERO DA FUNÇÃO AFIM... 6 FUNÇÕES CRESCENTES OU DECRESCENTES... 7 SINAL DE UMA
1. A partir da definição, determinar a equação da parábola P, cujo foco é F = (3, 4) e cuja diretriz é L : x + y 2 = 0. (x 3) 2 + (y + 4) 2 =
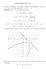 QUESTÕES-AULA 18 1. A partir da definição, determinar a equação da parábola P, cujo foco é F = (3, 4) e cuja diretriz é L : x + y = 0. Solução Seja P = (x, y) R. Temos que P P d(p, F ) = d(p, L) (x 3)
QUESTÕES-AULA 18 1. A partir da definição, determinar a equação da parábola P, cujo foco é F = (3, 4) e cuja diretriz é L : x + y = 0. Solução Seja P = (x, y) R. Temos que P P d(p, F ) = d(p, L) (x 3)
Curso de Geometria Analítica. Hipérbole
 Curso de Geometria Analítica Abrangência: Graduação em Engenharia e Matemática - Professor Responsável: Anastassios H. Kambourakis Resumo Teórico 03 - Cônicas- Circunferência, Elipse, Hipérbole e Parábola
Curso de Geometria Analítica Abrangência: Graduação em Engenharia e Matemática - Professor Responsável: Anastassios H. Kambourakis Resumo Teórico 03 - Cônicas- Circunferência, Elipse, Hipérbole e Parábola
GEOMETRIA ANALI TICA PONTO MEDIANA E BARICENTRO PLANO CARTESIANO DISTÂNCIA ENTRE DOIS PONTOS CONDIÇÃO DE ALINHAMENTO DE TRÊS PONTOS
 GEOMETRIA ANALI TICA PONTO PLANO CARTESIANO Vamos representar os pontos A (-2, 3) e B (4, -3) num plano cartesiano. MEDIANA E BARICENTRO A mediana é o segmento que une o ponto médio de um dos lados do
GEOMETRIA ANALI TICA PONTO PLANO CARTESIANO Vamos representar os pontos A (-2, 3) e B (4, -3) num plano cartesiano. MEDIANA E BARICENTRO A mediana é o segmento que une o ponto médio de um dos lados do
A(500, 500) B( 600, 600) C(715, 715) D( 1002, 1002) E(0, 0) F (711, 0) (c) ao terceiro quadrante? (d) ao quarto quadrante?
 Universidade Federal de Ouro Preto Departamento de Matemática MTM131 - Geometria Analítica e Cálculo Vetorial Professora: Monique Rafaella Anunciação de Oliveira Lista de Exercícios 1 1. Dados os pontos:
Universidade Federal de Ouro Preto Departamento de Matemática MTM131 - Geometria Analítica e Cálculo Vetorial Professora: Monique Rafaella Anunciação de Oliveira Lista de Exercícios 1 1. Dados os pontos:
Geometria Analítica I
 Geom. Analítica I Respostas do Módulo I - Aula 14 1 Geometria Analítica I 10/03/011 Respostas dos Exercícios do Módulo I - Aula 14 Aula 14 1. a. A equação do círculo de centro h, k) e raio r é x h) + y
Geom. Analítica I Respostas do Módulo I - Aula 14 1 Geometria Analítica I 10/03/011 Respostas dos Exercícios do Módulo I - Aula 14 Aula 14 1. a. A equação do círculo de centro h, k) e raio r é x h) + y
Módulo de Geometria Anaĺıtica Parte 2. Circunferência. Professores Tiago Miranda e Cleber Assis
 Módulo de Geometria Anaĺıtica Parte Circunferência a série E.M. Professores Tiago Miranda e Cleber Assis Geometria Analítica Parte Circunferência 1 Exercícios Introdutórios Exercício 1. Em cada item abaixo,
Módulo de Geometria Anaĺıtica Parte Circunferência a série E.M. Professores Tiago Miranda e Cleber Assis Geometria Analítica Parte Circunferência 1 Exercícios Introdutórios Exercício 1. Em cada item abaixo,
O problema proposto possui alguma solução? Se sim, quantas e quais são elas?
 PROVA PARA OS ALUNOS DE 3º ANO DO ENSINO MÉDIO 1) Considere o seguinte problema: Vitor ganhou R$ 3,20 de seu pai em moedas de 5 centavos, 10 centavos e 25 centavos. Se recebeu um total de 50 moedas, quantas
PROVA PARA OS ALUNOS DE 3º ANO DO ENSINO MÉDIO 1) Considere o seguinte problema: Vitor ganhou R$ 3,20 de seu pai em moedas de 5 centavos, 10 centavos e 25 centavos. Se recebeu um total de 50 moedas, quantas
Todos os exercícios sugeridos nesta apostila se referem ao volume 1. MATEMÁTICA I 1 FUNÇÃO EXPONENCIAL
 PROPRIEDADES DAS POTÊNCIAS... 2 FUNÇÃO EXPONENCIAL... 5 EQUAÇÕES EXPONENCIAIS... 10 INEQUAÇÕES EXPONENCIAIS... 17 RESPOSTAS... 22 REFERÊNCIA BIBLIOGRÁFICA... 24 No final das séries de exercícios podem
PROPRIEDADES DAS POTÊNCIAS... 2 FUNÇÃO EXPONENCIAL... 5 EQUAÇÕES EXPONENCIAIS... 10 INEQUAÇÕES EXPONENCIAIS... 17 RESPOSTAS... 22 REFERÊNCIA BIBLIOGRÁFICA... 24 No final das séries de exercícios podem
Aula Exemplos diversos. Exemplo 1
 Aula 3 1. Exemplos diversos Exemplo 1 Determine a equação da hipérbole equilátera, H, que passa pelo ponto Q = ( 1, ) e tem os eixos coordenados como assíntotas. Como as assíntotas da hipérbole são os
Aula 3 1. Exemplos diversos Exemplo 1 Determine a equação da hipérbole equilátera, H, que passa pelo ponto Q = ( 1, ) e tem os eixos coordenados como assíntotas. Como as assíntotas da hipérbole são os
6.1 equações canônicas de círculos e esferas
 6 C Í R C U LO S E E S F E R A S 6.1 equações canônicas de círculos e esferas Um círculo é o conjunto de pontos no plano que estão a uma certa distância r de um ponto dado (a, b). Desta forma temos que
6 C Í R C U LO S E E S F E R A S 6.1 equações canônicas de círculos e esferas Um círculo é o conjunto de pontos no plano que estão a uma certa distância r de um ponto dado (a, b). Desta forma temos que
1. Em cada caso, obtenha a equação e esboce o grá co da circunferência.
 3. AS CÔNICAS CÁLCULO VETORIAL - 2017.2 3.1 A circunferência 1. Em cada caso, obtenha a equação e esboce o grá co da circunferência. (a) Centro C ( 2; 1) e raio r = 5: (b) Passa pelos pontos A (5; 1) ;
3. AS CÔNICAS CÁLCULO VETORIAL - 2017.2 3.1 A circunferência 1. Em cada caso, obtenha a equação e esboce o grá co da circunferência. (a) Centro C ( 2; 1) e raio r = 5: (b) Passa pelos pontos A (5; 1) ;
RETA E CIRCUNFERÊNCIA
 RETA E CIRCUNFERÊNCIA - 016 1. (Unifesp 016) Na figura, as retas r, s e t estão em um mesmo plano cartesiano. Sabe-se que r e t passam pela origem desse sistema, e que PQRS é um trapézio. a) Determine
RETA E CIRCUNFERÊNCIA - 016 1. (Unifesp 016) Na figura, as retas r, s e t estão em um mesmo plano cartesiano. Sabe-se que r e t passam pela origem desse sistema, e que PQRS é um trapézio. a) Determine
Formação Continuada em MATEMÁTICA. Fundação CECIERJ/Consórcio CEDERJ. Matemática 3º Ano - 4º Bimestre/2013 Plano de Trabalho Geometria Analítica
 Formação Continuada em MATEMÁTICA Fundação CECIERJ/Consórcio CEDERJ Matemática 3º Ano - 4º Bimestre/2013 Plano de Trabalho Geometria Analítica Tarefa 2 Cursista: Rogério Galeazzi Galvagni Tutura: Maria
Formação Continuada em MATEMÁTICA Fundação CECIERJ/Consórcio CEDERJ Matemática 3º Ano - 4º Bimestre/2013 Plano de Trabalho Geometria Analítica Tarefa 2 Cursista: Rogério Galeazzi Galvagni Tutura: Maria
Consequentemente, fica fácil determinar os outros casos. Logicamente:
 4.. Posição relativa entre ponto e círculo. A linha, que é o círculo, divide o plano cartesiano em duas partes, a interior e a exterior, assim um ponto tem chance de pertencer a três lugares: P interior
4.. Posição relativa entre ponto e círculo. A linha, que é o círculo, divide o plano cartesiano em duas partes, a interior e a exterior, assim um ponto tem chance de pertencer a três lugares: P interior
Exercícios de Matemática Geometria Analítica
 Eercícios de Matemática Geometria Analítica. (UFRGS) Considere um sistema cartesiano ortogonal e o ponto P(. ) de intersecção das duas diagonais de um losango. Se a equação da reta que contém uma das diagonais
Eercícios de Matemática Geometria Analítica. (UFRGS) Considere um sistema cartesiano ortogonal e o ponto P(. ) de intersecção das duas diagonais de um losango. Se a equação da reta que contém uma das diagonais
Notas de Aulas 3 - Cônicas Prof Carlos A S Soares
 Notas de Aulas 3 - Cônicas Prof Carlos A S Soares 1 Parábolas 1.1 Conceito e Elementos Definição 1.1 Sejam l uma reta e F um ponto não pertencente a l. Chamamos parábola de diretriz l e foco F o conjunto
Notas de Aulas 3 - Cônicas Prof Carlos A S Soares 1 Parábolas 1.1 Conceito e Elementos Definição 1.1 Sejam l uma reta e F um ponto não pertencente a l. Chamamos parábola de diretriz l e foco F o conjunto
O ESTUDO DA CIRCUNFERÊNCIA
 Hewlett-Packard O ESTUDO DA CIRCUNFERÊNCIA Aulas 01 a 05 Sumário EQUAÇÃO REDUZIDA DA CIRCUNFERÊNCIA...... EQUAÇÃO GERAL DA CIRCUNFERÊNCIA......... POSIÇÃO RELATIVA ENTRE UM PONTO E UMA CIRCUNFERÊNCIA...
Hewlett-Packard O ESTUDO DA CIRCUNFERÊNCIA Aulas 01 a 05 Sumário EQUAÇÃO REDUZIDA DA CIRCUNFERÊNCIA...... EQUAÇÃO GERAL DA CIRCUNFERÊNCIA......... POSIÇÃO RELATIVA ENTRE UM PONTO E UMA CIRCUNFERÊNCIA...
3.2 Determine a equação da circunferência de raio 5, tangente à reta 3x +4y =16no ponto A (4, 1).
 3.1 Obtenha a equação e esboce o gráfico da circunferência caracterizada por: (a) Centro C (, 1) eraior =5; (b) Passa pelos pontos A (1, ),B(1, 1) e C (, 3) ; (c) Inscrita no triângulo determinado pelas
3.1 Obtenha a equação e esboce o gráfico da circunferência caracterizada por: (a) Centro C (, 1) eraior =5; (b) Passa pelos pontos A (1, ),B(1, 1) e C (, 3) ; (c) Inscrita no triângulo determinado pelas
Matemática B Semi-Extensivo V. 3
 GRITO Matemática Semi-Etensivo V. (, e (, M, Então: M = M = M = M = Eercícios D Substituindo em I, temos: = =. = = Então, = ( = 8 M(, (, (, M = M = 8 M = M = D Sabendo que o eio é o da abcissa e que o
GRITO Matemática Semi-Etensivo V. (, e (, M, Então: M = M = M = M = Eercícios D Substituindo em I, temos: = =. = = Então, = ( = 8 M(, (, (, M = M = 8 M = M = D Sabendo que o eio é o da abcissa e que o
13. (Uerj) Em cada ponto (x, y) do plano cartesiano, o valor de T é definido pela seguinte equação:
 1. (Ufc) Considere o triângulo cujos vértices são os pontos A(2,0); B(0,4) e C(2Ë5, 4+Ë5). Determine o valor numérico da altura relativa ao lado AB, deste triângulo. 2. (Unesp) A reta r é perpendicular
1. (Ufc) Considere o triângulo cujos vértices são os pontos A(2,0); B(0,4) e C(2Ë5, 4+Ë5). Determine o valor numérico da altura relativa ao lado AB, deste triângulo. 2. (Unesp) A reta r é perpendicular
Todos os exercícios sugeridos nesta apostila se referem ao volume 1. MATEMÁTICA I 1 CONJUNTOS NUMÉRICOS
 CONJUNTO DOS NÚMEROS NATURAIS... 2 RETA NUMERADA... 2 CONJUNTO DOS NÚMEROS INTEIROS... 4 SUBCONJUNTOS DE Z... 5 NÚMEROS OPOSTOS... 5 VALOR ABSOLUTO DE UM NÚMERO INTEIRO... 6 CONJUNTO DOS NÚMEROS RACIONAIS...
CONJUNTO DOS NÚMEROS NATURAIS... 2 RETA NUMERADA... 2 CONJUNTO DOS NÚMEROS INTEIROS... 4 SUBCONJUNTOS DE Z... 5 NÚMEROS OPOSTOS... 5 VALOR ABSOLUTO DE UM NÚMERO INTEIRO... 6 CONJUNTO DOS NÚMEROS RACIONAIS...
Matemática B Extensivo v. 8
 Etensivo v. 8 Eercícios 0) 9 6 = ; e = 3 centro Note que C = (0, 0). Também, c = e a = 3. Então, da equação c = b + a temos = b + 3 b = 4. Assim, a equação dessa hipérbole fica: = = 3 4 9 6 A ecentricidade
Etensivo v. 8 Eercícios 0) 9 6 = ; e = 3 centro Note que C = (0, 0). Também, c = e a = 3. Então, da equação c = b + a temos = b + 3 b = 4. Assim, a equação dessa hipérbole fica: = = 3 4 9 6 A ecentricidade
ADA 1º BIMESTRE CICLO I MATEMÁTICA 3ª SÉRIE DO ENSINO MÉDIO. (B)y = x + 3 (C)y = 2x + 3 (D)y = 3x - 3 (E)y = 5x + 5 Gabarito: D.
 ADA 1º BIMESTRE CICLO I MATEMÁTICA ª SÉRIE DO ENSINO MÉDIO ITEM 1 DA ADA Observe as equações da reta a seguir: I) y = x 1 II) y 4x = III) y 4x + = 0 IV) y + 1 = x V) y + 1 = (x 1 ) Dessas equações, a que
ADA 1º BIMESTRE CICLO I MATEMÁTICA ª SÉRIE DO ENSINO MÉDIO ITEM 1 DA ADA Observe as equações da reta a seguir: I) y = x 1 II) y 4x = III) y 4x + = 0 IV) y + 1 = x V) y + 1 = (x 1 ) Dessas equações, a que
Capítulo 2. Retas no plano. 1. Retas verticais e não-verticais. Definição 1
 Capítulo 2 Retas no plano O objetivo desta aula é determinar a equação algébrica que representa uma reta no plano. Para isso, vamos analisar separadamente dois tipos de reta: reta vertical e reta não-vertical.
Capítulo 2 Retas no plano O objetivo desta aula é determinar a equação algébrica que representa uma reta no plano. Para isso, vamos analisar separadamente dois tipos de reta: reta vertical e reta não-vertical.
Introdução: A necessidade de ampliação dos conjuntos Numéricos. Considere incialmente o conjunto dos números naturais :
 Introdução: A necessidade de ampliação dos conjuntos Numéricos Considere incialmente o conjunto dos números naturais : Neste conjunto podemos resolver uma infinidade de equações do tipo A solução pertence
Introdução: A necessidade de ampliação dos conjuntos Numéricos Considere incialmente o conjunto dos números naturais : Neste conjunto podemos resolver uma infinidade de equações do tipo A solução pertence
INSTITUTO FEDERAL DE BRASILIA 3ª Lista GABARITO DATA: 14/09/2016
 INSTITUTO FEDERAL DE BRASILIA ª Lista MATEMÁTICA GEOMETRIA ANALÍTICA GABARITO DATA: 14/09/016 1) No plano cartesiano, 0xy, a circunferência C tem centro no ponto P (, 1), e a reta t é tangente a C no ponto
INSTITUTO FEDERAL DE BRASILIA ª Lista MATEMÁTICA GEOMETRIA ANALÍTICA GABARITO DATA: 14/09/016 1) No plano cartesiano, 0xy, a circunferência C tem centro no ponto P (, 1), e a reta t é tangente a C no ponto
Circunferências. λ : x y 4x 10y λ : x y 4x 5y 12 0
 Circunferências 1. (Espcex (Aman) 014) Sejam dados a circunferência λ : x y 4x 10y 5 0 e o ponto P, que é simétrico de ( 1, 1) em relação ao eixo das abscissas. Determine a equação da circunferência concêntrica
Circunferências 1. (Espcex (Aman) 014) Sejam dados a circunferência λ : x y 4x 10y 5 0 e o ponto P, que é simétrico de ( 1, 1) em relação ao eixo das abscissas. Determine a equação da circunferência concêntrica
Aula 10 Regiões e inequações no plano
 MÓDULO 1 - AULA 10 Aula 10 Regiões e inequações no plano Objetivos Resolver inequações do segundo grau. Analisar sistemas envolvendo inequações do primeiro e segundo graus. Resolver inequações modulares
MÓDULO 1 - AULA 10 Aula 10 Regiões e inequações no plano Objetivos Resolver inequações do segundo grau. Analisar sistemas envolvendo inequações do primeiro e segundo graus. Resolver inequações modulares
Matemática B Extensivo V. 7
 GRITO Matemática Etensivo V. 7 Eercícios ) D ) D ) I. Falso. O diâmetro é dado por. r. cm. II. Verdadeiro. o volume é dado por π. r² π. ² π cm² III. Verdadeiro. (, ) (, ) e assim, ( )² + ( )² r² fica ²
GRITO Matemática Etensivo V. 7 Eercícios ) D ) D ) I. Falso. O diâmetro é dado por. r. cm. II. Verdadeiro. o volume é dado por π. r² π. ² π cm² III. Verdadeiro. (, ) (, ) e assim, ( )² + ( )² r² fica ²
ITA º DIA MATEMÁTICA BERNOULLI COLÉGIO E PRÉ-VESTIBULAR
 ITA - 2006 3º DIA MATEMÁTICA BERNOULLI COLÉGIO E PRÉ-VESTIBULAR Matemática Questão 01 Seja E um ponto externo a uma circunferência. Os segmentos e interceptam essa circunferência nos pontos B e A, e, C
ITA - 2006 3º DIA MATEMÁTICA BERNOULLI COLÉGIO E PRÉ-VESTIBULAR Matemática Questão 01 Seja E um ponto externo a uma circunferência. Os segmentos e interceptam essa circunferência nos pontos B e A, e, C
Aula Elipse. Definição 1. Nosso objetivo agora é estudar a equação geral do segundo grau em duas variáveis:
 Aula 18 Nosso objetivo agora é estudar a equação geral do segundo grau em duas variáveis: Ax + Bxy + Cy + Dx + Ey + F = 0, onde A 0 ou B 0 ou C 0 Vamos considerar primeiro os casos em que B = 0. Isto é,
Aula 18 Nosso objetivo agora é estudar a equação geral do segundo grau em duas variáveis: Ax + Bxy + Cy + Dx + Ey + F = 0, onde A 0 ou B 0 ou C 0 Vamos considerar primeiro os casos em que B = 0. Isto é,
Aula 2 A distância no espaço
 MÓDULO 1 - AULA 2 Objetivos Aula 2 A distância no espaço Determinar a distância entre dois pontos do espaço. Estabelecer a equação da esfera em termos de distância. Estudar a posição relativa entre duas
MÓDULO 1 - AULA 2 Objetivos Aula 2 A distância no espaço Determinar a distância entre dois pontos do espaço. Estabelecer a equação da esfera em termos de distância. Estudar a posição relativa entre duas
Título do Livro. Capítulo 5
 Capítulo 5 5. Geometria Analítica A Geometria Analítica tornou possível o estudo da Geometria através da Álgebra. Além de proporcionar a interpretação geométrica de diversas equações algébricas. 5.1. Sistema
Capítulo 5 5. Geometria Analítica A Geometria Analítica tornou possível o estudo da Geometria através da Álgebra. Além de proporcionar a interpretação geométrica de diversas equações algébricas. 5.1. Sistema
Duas retas distintas irão assumir as seguintes posições relativas no espaço:
 Posições relativas As figuras planas e espaciais são formadas pela intersecção de retas e planos pertencentes ao espaço. Dentre as posições relativas, podemos destacar: Posição relativa entre duas retas
Posições relativas As figuras planas e espaciais são formadas pela intersecção de retas e planos pertencentes ao espaço. Dentre as posições relativas, podemos destacar: Posição relativa entre duas retas
A primeira coisa a fazer é saber quais são as equações das curvas quando elas já se encontram na melhor
 Identificação de Cônicas Uma equação do segundo grau ax + bxy + cy + dx + ey + f = 0 define de maneira implícita uma curva no plano xy: o conjunto dos pontos (x, y) que satisfazem a equação. Por exemplo,
Identificação de Cônicas Uma equação do segundo grau ax + bxy + cy + dx + ey + f = 0 define de maneira implícita uma curva no plano xy: o conjunto dos pontos (x, y) que satisfazem a equação. Por exemplo,
Plano Cartesiano e Retas. Vitor Bruno Engenharia Civil
 Plano Cartesiano e Retas Vitor Bruno Engenharia Civil Sistema cartesiano ortogonal O sistema cartesiano ortogonal é formado por dois eixos ortogonais(eixo x e eixo y). A intersecção dos eixos x e y é o
Plano Cartesiano e Retas Vitor Bruno Engenharia Civil Sistema cartesiano ortogonal O sistema cartesiano ortogonal é formado por dois eixos ortogonais(eixo x e eixo y). A intersecção dos eixos x e y é o
Matemática B Intensivo V. 2
 Matemática Intensivo V. Eercícios ) ) C ( ) (5 7) Usando a fórmula do ponto médio: X + X Y + Y C + 5 + 7 6 8 ( ) ERRT: considere (6 ). Temos d () d (C). ssim: ( 6) + ( b ) ( ) + ( 6 b) 9 + b 9 + b b +
Matemática Intensivo V. Eercícios ) ) C ( ) (5 7) Usando a fórmula do ponto médio: X + X Y + Y C + 5 + 7 6 8 ( ) ERRT: considere (6 ). Temos d () d (C). ssim: ( 6) + ( b ) ( ) + ( 6 b) 9 + b 9 + b b +
Colégio Notre Dame de Campinas Congregação de Santa Cruz PLANTÕES DE JULHO MATEMÁTICA AULA 1
 PLANTÕES DE JULHO MATEMÁTICA AULA 1 Nome: Nº: Série: 3º ANO Turma: Prof: Luis Felipe Bortoletto Data: JULHO 2018 Lista 1 1) Após acionar um flash de uma câmera, a bateria imediatamente começa a recarregar
PLANTÕES DE JULHO MATEMÁTICA AULA 1 Nome: Nº: Série: 3º ANO Turma: Prof: Luis Felipe Bortoletto Data: JULHO 2018 Lista 1 1) Após acionar um flash de uma câmera, a bateria imediatamente começa a recarregar
Professor Mascena Cordeiro
 www.mascenacordeiro.com Professor Mascena Cordeiro º Ano Ensino Médio M A T E M Á T I C A. Determine os valores de m pertencentes ao conjunto dos números reais, tal que os pontos (0, -), (, m) e (-, -)
www.mascenacordeiro.com Professor Mascena Cordeiro º Ano Ensino Médio M A T E M Á T I C A. Determine os valores de m pertencentes ao conjunto dos números reais, tal que os pontos (0, -), (, m) e (-, -)
Retas e círculos, posições relativas e distância de um ponto a uma reta
 Capítulo 3 Retas e círculos, posições relativas e distância de um ponto a uma reta Nesta aula vamos caracterizar de forma algébrica a posição relativa de duas retas no plano e de uma reta e de um círculo
Capítulo 3 Retas e círculos, posições relativas e distância de um ponto a uma reta Nesta aula vamos caracterizar de forma algébrica a posição relativa de duas retas no plano e de uma reta e de um círculo
PROFESSOR FLABER 2ª SÉRIE Circunferência
 PROFESSOR FLABER ª SÉRIE Circunferência 01. (Fuvest SP) A reta s passa pelo ponto (0,3) e é perpendicular à reta AB onde A=(0,0) e B é o centro da circunferência x + y - x - 4y = 0. Então a equação de
PROFESSOR FLABER ª SÉRIE Circunferência 01. (Fuvest SP) A reta s passa pelo ponto (0,3) e é perpendicular à reta AB onde A=(0,0) e B é o centro da circunferência x + y - x - 4y = 0. Então a equação de
Matemática - 3ª série Roteiro 04 Caderno do Aluno. Estudo da Reta
 Matemática - 3ª série Roteiro 04 Caderno do Aluno Estudo da Reta I - Inclinação de uma reta () direção É a medida do ângulo que a reta forma com o semieixo das abscissas (positivo) no sentido anti-horário.
Matemática - 3ª série Roteiro 04 Caderno do Aluno Estudo da Reta I - Inclinação de uma reta () direção É a medida do ângulo que a reta forma com o semieixo das abscissas (positivo) no sentido anti-horário.
Instituto Federal de Educação, Ciência e Tecnologia Rio Grande do Sul Campus Rio Grande CAPÍTULO 4 GEOMETRIA ANALÍTICA
 Instituto Federal de Educação, Ciência e Tecnologia Rio Grande do Sul Campus Rio Grande CAPÍTULO 4 GEOMETRIA ANALÍTICA 4. Geometria Analítica 4.1. Introdução Geometria Analítica é a parte da Matemática,
Instituto Federal de Educação, Ciência e Tecnologia Rio Grande do Sul Campus Rio Grande CAPÍTULO 4 GEOMETRIA ANALÍTICA 4. Geometria Analítica 4.1. Introdução Geometria Analítica é a parte da Matemática,
Função do 2 o Grau. 11.Sinal da função quadrática 12.Inequação do 2 o grau
 UNIVERSIDADE DO ESTADO DE MATO GROSSO CAMPUS UNIVERSITÁRIO DE SINOP FACULDADE DE CIÊNCIAS EXATAS E TECNOLÓGICAS CURSO DE ENGENHARIA CIVIL DISCIPLINA: FUNDAMENTOS DE MATEMÁTICA Função do o Grau Prof.: Rogério
UNIVERSIDADE DO ESTADO DE MATO GROSSO CAMPUS UNIVERSITÁRIO DE SINOP FACULDADE DE CIÊNCIAS EXATAS E TECNOLÓGICAS CURSO DE ENGENHARIA CIVIL DISCIPLINA: FUNDAMENTOS DE MATEMÁTICA Função do o Grau Prof.: Rogério
3º trimestre SALA DE ESTUDOS Data: 11/17 Ensino Médio 3º ano A, B e C. Prof. Maurício Nome: nº
 º trimestre SALA DE ESTUDOS Data: 11/17 Ensino Médio º ano A, B e C. Prof. Maurício Nome: nº CONTEÚDOS: EQUAÇÃO DA RETA E EQUAÇÃO DA CIRCUNFERÊNCIA. 1. (Eear 017) O triângulo ABC a) escaleno b) isósceles
º trimestre SALA DE ESTUDOS Data: 11/17 Ensino Médio º ano A, B e C. Prof. Maurício Nome: nº CONTEÚDOS: EQUAÇÃO DA RETA E EQUAÇÃO DA CIRCUNFERÊNCIA. 1. (Eear 017) O triângulo ABC a) escaleno b) isósceles
Ricardo Bianconi. Fevereiro de 2015
 Seções Cônicas Ricardo Bianconi Fevereiro de 2015 Uma parte importante da Geometria Analítica é o estudo das curvas planas e, em particular, das cônicas. Neste texto estudamos algumas propriedades das
Seções Cônicas Ricardo Bianconi Fevereiro de 2015 Uma parte importante da Geometria Analítica é o estudo das curvas planas e, em particular, das cônicas. Neste texto estudamos algumas propriedades das
Formação Continuada em MATEMÁTICA Fundação CECIERJ/Consórcio CEDERJ. Matemática 3º Ano 4º Bimestre/2014 Plano de Trabalho 2. Geometria Analítica
 Formação Continuada em MATEMÁTICA Fundação CECIERJ/Consórcio CEDERJ Matemática 3º Ano 4º Bimestre/2014 Plano de Trabalho 2 Geometria Analítica http://exilioandarilho.blogspot.com/2009_03_01_archive.html
Formação Continuada em MATEMÁTICA Fundação CECIERJ/Consórcio CEDERJ Matemática 3º Ano 4º Bimestre/2014 Plano de Trabalho 2 Geometria Analítica http://exilioandarilho.blogspot.com/2009_03_01_archive.html
matemática geometria analítica pontos, baricentro do triângulo, coeficiente angular e equações da reta Exercícios de distância entre dois pontos
 Exercícios de distância entre dois pontos 1. (FUVEST 1ª fase) Sejam A = (1, ) e B = (3, ) dois pontos do plano cartesiano. Nesse plano, o segmento AC é obtido do segmento AB por uma rotação de 60º, no
Exercícios de distância entre dois pontos 1. (FUVEST 1ª fase) Sejam A = (1, ) e B = (3, ) dois pontos do plano cartesiano. Nesse plano, o segmento AC é obtido do segmento AB por uma rotação de 60º, no
54 CAPÍTULO 2. GEOMETRIA ANALÍTICA ( ) =
 54 CAPÍTULO. GEOMETRIA ANALÍTICA.5 Cônicas O grá co da equação + + + + + = 0 (.4) onde,,,, e são constantes com, e, não todos nulos, é uma cônica. A equação (.4) é chamada de equação geral do grau em e
54 CAPÍTULO. GEOMETRIA ANALÍTICA.5 Cônicas O grá co da equação + + + + + = 0 (.4) onde,,,, e são constantes com, e, não todos nulos, é uma cônica. A equação (.4) é chamada de equação geral do grau em e
GEOMETRIA ANALÍTICA 2017
 GEOMETRIA ANALÍTICA 2017 Tópicos a serem estudados 1) O ponto (Noções iniciais - Reta orientada ou eixo Razão de segmentos Noções Simetria Plano Cartesiano Abcissas e Ordenadas Ponto Médio Baricentro -
GEOMETRIA ANALÍTICA 2017 Tópicos a serem estudados 1) O ponto (Noções iniciais - Reta orientada ou eixo Razão de segmentos Noções Simetria Plano Cartesiano Abcissas e Ordenadas Ponto Médio Baricentro -
54 CAPÍTULO 2. GEOMETRIA ANALÍTICA ( ) =
 54 CAPÍTULO. GEOMETRIA ANALÍTICA.5 Cônicas O grá co da equação + + + + + = 0 (.4) onde,,,, e são constantes com, e, não todos nulos, é uma cônica. A equação (.4) é chamada de equação geral do grau em e
54 CAPÍTULO. GEOMETRIA ANALÍTICA.5 Cônicas O grá co da equação + + + + + = 0 (.4) onde,,,, e são constantes com, e, não todos nulos, é uma cônica. A equação (.4) é chamada de equação geral do grau em e
Geometria Analítica - AFA
 Geometria Analítica - AFA x = v + (AFA) Considerando no plano cartesiano ortogonal as retas r, s e t, tais que (r) :, (s) : mx + y + m = 0 e (t) : x = 0, y = v analise as proposições abaixo, classificando-
Geometria Analítica - AFA x = v + (AFA) Considerando no plano cartesiano ortogonal as retas r, s e t, tais que (r) :, (s) : mx + y + m = 0 e (t) : x = 0, y = v analise as proposições abaixo, classificando-
Escola Secundária com 3º ciclo D. Dinis 10º Ano de Matemática A Funções e Gráficos Generalidades. Funções polinomiais. Função módulo.
 Escola Secundária com 3º ciclo D. Dinis 10º Ano de Matemática A Funções e Gráficos Generalidades. Funções polinomiais. Função módulo. Trabalho de casa nº 10 1. Na figura está representado, num referencial
Escola Secundária com 3º ciclo D. Dinis 10º Ano de Matemática A Funções e Gráficos Generalidades. Funções polinomiais. Função módulo. Trabalho de casa nº 10 1. Na figura está representado, num referencial
0 < c < a ; d(f 1, F 2 ) = 2c
 Capítulo 14 Elipse Nosso objetivo, neste e nos próximos capítulos, é estudar a equação geral do segundo grau em duas variáveis: Ax + Bxy + Cy + Dx + Ey + F = 0, onde A 0 ou B 0 ou C 0 Para isso, deniremos,
Capítulo 14 Elipse Nosso objetivo, neste e nos próximos capítulos, é estudar a equação geral do segundo grau em duas variáveis: Ax + Bxy + Cy + Dx + Ey + F = 0, onde A 0 ou B 0 ou C 0 Para isso, deniremos,
Polígonos PROFESSOR RANILDO LOPES 11.1
 Polígonos PROFESSOR RANILDO LOPES 11.1 Polígonos Polígono é uma figura geométrica plana e fechada formada apenas por segmentos de reta que não se cruzam no mesmo plano. Exemplos 11.1 Elementos de um polígono
Polígonos PROFESSOR RANILDO LOPES 11.1 Polígonos Polígono é uma figura geométrica plana e fechada formada apenas por segmentos de reta que não se cruzam no mesmo plano. Exemplos 11.1 Elementos de um polígono
02 Do ponto P exterior a uma circunferência tiramos uma secante que corta a
 01 Em um triângulo AB AC 5 cm e BC cm. Tomando-se sobre AB e AC os pontos D e E, respectivamente, de maneira que DE seja paralela a BC e que o quadrilátero BCED seja circunscritível a um círculo, a distância
01 Em um triângulo AB AC 5 cm e BC cm. Tomando-se sobre AB e AC os pontos D e E, respectivamente, de maneira que DE seja paralela a BC e que o quadrilátero BCED seja circunscritível a um círculo, a distância
Formação Continuada em Matemática Fundação CICIERJ/Consórcio Cederj. Matemática 3º Ano 4º Bimestre/2014. Plano de Trabalho
 Formação Continuada em Matemática Fundação CICIERJ/Consórcio Cederj Matemática 3º Ano 4º Bimestre/2014 Plano de Trabalho GEOMETRIA ANALÍTICA: retas paralelas e retas perpendiculares a partir de suas equações
Formação Continuada em Matemática Fundação CICIERJ/Consórcio Cederj Matemática 3º Ano 4º Bimestre/2014 Plano de Trabalho GEOMETRIA ANALÍTICA: retas paralelas e retas perpendiculares a partir de suas equações
UNIVERSIDADE FEDERAL DE PERNAMBUCO
 CÁLCULO L1 NOTAS DA PRIMEIRA AULA UNIVERSIDADE FEDERAL DE PERNAMBUCO Resumo. Nesta aula discutiremos como obter as equações das retas tangentes a uma curva planar que é o gráfico de uma função. 1. Introdução
CÁLCULO L1 NOTAS DA PRIMEIRA AULA UNIVERSIDADE FEDERAL DE PERNAMBUCO Resumo. Nesta aula discutiremos como obter as equações das retas tangentes a uma curva planar que é o gráfico de uma função. 1. Introdução
Questão 1 a) A(0; 0) e B(8; 12) b) A(-4; 8) e B(3; -9) c) A(3; -5) e B(6; -2) d) A(2; 3) e B(1/2; 2/3) e) n.d.a.
 APOSTILAS (ENEM) VOLUME COMPLETO Exame Nacional de Ensino Médio (ENEM) 4 VOLUMES APOSTILAS IMPRESSAS E DIGITAIS Questão 1 (UFPE) Determine o ponto médio dos segmentos seguintes, que têm medidas inteiras:
APOSTILAS (ENEM) VOLUME COMPLETO Exame Nacional de Ensino Médio (ENEM) 4 VOLUMES APOSTILAS IMPRESSAS E DIGITAIS Questão 1 (UFPE) Determine o ponto médio dos segmentos seguintes, que têm medidas inteiras:
EXERCICIOS DE APROFUNDAMENTO - MATEMÁTICA - RETA
 EXERCICIOS DE APROFUNDAMENTO - MATEMÁTICA - RETA - 015 1. (Unicamp 015) Seja r a reta de equação cartesiana x y 4. Para cada número real t tal que 0 t 4, considere o triângulo T de vértices em (0, 0),
EXERCICIOS DE APROFUNDAMENTO - MATEMÁTICA - RETA - 015 1. (Unicamp 015) Seja r a reta de equação cartesiana x y 4. Para cada número real t tal que 0 t 4, considere o triângulo T de vértices em (0, 0),
Aula 7 Equação Vetorial da Reta e Equação Vetorial do plano
 Aula 7 Equação Vetorial da Reta e Equação Vetorial do plano Prof Luis Carlos As retas podem estar posicionadas em planos (R 2 ) ou no espaço (R 3 ). Retas no plano possuem pontos com duas coordenadas,
Aula 7 Equação Vetorial da Reta e Equação Vetorial do plano Prof Luis Carlos As retas podem estar posicionadas em planos (R 2 ) ou no espaço (R 3 ). Retas no plano possuem pontos com duas coordenadas,
Equações de 2º grau. Denomina-se equação do 2º grau na incógnita x, toda equação da forma: IR e
 Equações de 2º grau Definições Denomina-se equação do 2º grau na incógnita x, toda equação da forma: ax 2 + bx + c = 0; a, b, c IR e Exemplo: x 2-5x + 6 = 0 é um equação do 2º grau com a = 1, b = -5 e
Equações de 2º grau Definições Denomina-se equação do 2º grau na incógnita x, toda equação da forma: ax 2 + bx + c = 0; a, b, c IR e Exemplo: x 2-5x + 6 = 0 é um equação do 2º grau com a = 1, b = -5 e
Aula 14 Círculo. Objetivos
 Aula 1 Círculo MÓDULO 1 - AULA 1 Objetivos Determinar a equação do círculo de centro C e raio r, como um lugar geométrico. Aprender os conceitos de retas tangente e normal num ponto P de um círculo. Esboçar
Aula 1 Círculo MÓDULO 1 - AULA 1 Objetivos Determinar a equação do círculo de centro C e raio r, como um lugar geométrico. Aprender os conceitos de retas tangente e normal num ponto P de um círculo. Esboçar
Resumo: Nestas notas faremos um breve estudo sobre as principais propriedades. mínimos, gráficos e algumas aplicações simples.
 Universidade Estadual de Maringá - Departamento de Matemática Cálculo Diferencial e Integral: um KIT de Sobrevivência c Publicação Eletrônica do KIT http://www.dma.uem.br/kit Equação quadrática Prof. Doherty
Universidade Estadual de Maringá - Departamento de Matemática Cálculo Diferencial e Integral: um KIT de Sobrevivência c Publicação Eletrônica do KIT http://www.dma.uem.br/kit Equação quadrática Prof. Doherty
Distância entre duas retas. Regiões no plano
 Capítulo 4 Distância entre duas retas. Regiões no plano Nesta aula, veremos primeiro como podemos determinar a distância entre duas retas paralelas no plano. Para isso, lembramos que, na aula anterior,
Capítulo 4 Distância entre duas retas. Regiões no plano Nesta aula, veremos primeiro como podemos determinar a distância entre duas retas paralelas no plano. Para isso, lembramos que, na aula anterior,
( ) ( ) FUVEST 08/01/ /11/2008 Seu pé direito nas melhores Faculdades MATEMÁTICA
 FUVEST 08/0/009 //008 Seu pé direito nas melhores Faculdades MTEMÁTIC 0. Na figura, a reta r tem equação y x + no plano cartesiano Oxy. lém disso, os pontos 0,,, estão na reta r, sendo 0 0,). Os pontos
FUVEST 08/0/009 //008 Seu pé direito nas melhores Faculdades MTEMÁTIC 0. Na figura, a reta r tem equação y x + no plano cartesiano Oxy. lém disso, os pontos 0,,, estão na reta r, sendo 0 0,). Os pontos
a é sempre o coeficiente de x²; b é sempre o coeficiente de x, c é o coeficiente ou termo independente.
 Definições Denomina-se equação do 2º grau na incógnita x, toda equação da forma: ax 2 + bx + c = 0; a, b, c Exemplo: x 2-5x + 6 = 0 é um equação do 2º grau com a = 1, b = -5 e c = 6. 6x 2 - x - 1 = 0 é
Definições Denomina-se equação do 2º grau na incógnita x, toda equação da forma: ax 2 + bx + c = 0; a, b, c Exemplo: x 2-5x + 6 = 0 é um equação do 2º grau com a = 1, b = -5 e c = 6. 6x 2 - x - 1 = 0 é
Resumo: Nestas notas faremos um breve estudo sobre as principais propriedades. mínimos, gráficos e algumas aplicações simples.
 Universidade Estadual de Maringá - Departamento de Matemática Cálculo Diferencial e Integral: um KIT de Sobrevivência c Publicação Eletrônica do KIT http://www.dma.uem.br/kit Equação quadrática Prof. Doherty
Universidade Estadual de Maringá - Departamento de Matemática Cálculo Diferencial e Integral: um KIT de Sobrevivência c Publicação Eletrônica do KIT http://www.dma.uem.br/kit Equação quadrática Prof. Doherty
J. Delgado - K. Frensel - L. Crissaff Geometria Analítica e Cálculo Vetorial
 76 Capítulo 4 Distâncias no plano e regiões no plano 1. Distância de um ponto a uma reta Dados um ponto P e uma reta r no plano, já sabemos calcular a distância de P a cada ponto P r. Definição 1 Definimos
76 Capítulo 4 Distâncias no plano e regiões no plano 1. Distância de um ponto a uma reta Dados um ponto P e uma reta r no plano, já sabemos calcular a distância de P a cada ponto P r. Definição 1 Definimos
Geometria Analítica? Onde usar os conhecimentos. os sobre Geometria Analítica?
 X GEOMETRIA ANALÍTICA Por que aprender Geometria Analítica?... A Geometria Analítica estabelece relações entre a álgebra e a geometria por meio de equações e inequações. Isso permite transformar questões
X GEOMETRIA ANALÍTICA Por que aprender Geometria Analítica?... A Geometria Analítica estabelece relações entre a álgebra e a geometria por meio de equações e inequações. Isso permite transformar questões
Ponto 1) Representação do Ponto
 Ponto 1) Representação do Ponto Universidade Federal de Pelotas Cálculo com Geometria Analítica I Prof a : Msc. Merhy Heli Rodrigues Plano Cartesiano, sistemas de coordenadas: pontos e retas Na geometria
Ponto 1) Representação do Ponto Universidade Federal de Pelotas Cálculo com Geometria Analítica I Prof a : Msc. Merhy Heli Rodrigues Plano Cartesiano, sistemas de coordenadas: pontos e retas Na geometria
r : Exemplo: Considere a reta r :
 4.7. Equação paramétrica da reta. Também podemos representar uma reta no plano com equação paramétrica, mas no plano temos apenas duas coordenadas. A forma paramétrica de uma reta no plano é: x a r : y
4.7. Equação paramétrica da reta. Também podemos representar uma reta no plano com equação paramétrica, mas no plano temos apenas duas coordenadas. A forma paramétrica de uma reta no plano é: x a r : y
Exercícios de Revisão 1º Ano Ensino Médio Prof. Osmar 2º. BIMESTRE
 Exercícios de Revisão 1º Ano Ensino Médio Prof. Osmar º. BIMESTRE I PORCENTAGEM 1. Qual o montante, após dois anos, em uma aplicação que rende 10% ao semestre ( juros compostos), sabendo que o capital
Exercícios de Revisão 1º Ano Ensino Médio Prof. Osmar º. BIMESTRE I PORCENTAGEM 1. Qual o montante, após dois anos, em uma aplicação que rende 10% ao semestre ( juros compostos), sabendo que o capital
Universidade Federal do Pará Curso de Licenciatura em Matemática PARFOR Lista de Exercícios Referentes a Prova Substitutiva de Geometria Analítica
 1 Universidade Federal do Pará Curso de Licenciatura em Matemática PARFOR Lista de Exercícios Referentes a Prova Substitutiva de Geometria Analítica 1. Determine a distância entre os pontos A(-2, 7) e
1 Universidade Federal do Pará Curso de Licenciatura em Matemática PARFOR Lista de Exercícios Referentes a Prova Substitutiva de Geometria Analítica 1. Determine a distância entre os pontos A(-2, 7) e
Matemática. Resolução das atividades complementares. M21 Geometria Analítica: Cônicas
 Resolução das atividades complementares Matemática M Geometria Analítica: Cônicas p. FGV-SP) Determine a equação da elipse de centro na origem que passa pelos pontos A, 0), B, 0) e C0, ). O centro da elipse
Resolução das atividades complementares Matemática M Geometria Analítica: Cônicas p. FGV-SP) Determine a equação da elipse de centro na origem que passa pelos pontos A, 0), B, 0) e C0, ). O centro da elipse
EXERCÍCIOS DE RECUPERAÇÃO DE GEOMETRIA 2º TRIMESTRE FORMULÁRIO
 EXERCÍCIOS DE RECUPERAÇÃO DE GEOMETRIA º TRIMESTRE Nome: nº: Ano:ºA E.M. Data: / / 018 Professora: Lilian Caccuri x A x B ya y Ponto médio: M ; yb ya Coeficiente angular: m x x 1) As retas x - y = 3 e
EXERCÍCIOS DE RECUPERAÇÃO DE GEOMETRIA º TRIMESTRE Nome: nº: Ano:ºA E.M. Data: / / 018 Professora: Lilian Caccuri x A x B ya y Ponto médio: M ; yb ya Coeficiente angular: m x x 1) As retas x - y = 3 e
Fundação CECIERJ/ Consórcio CEDERJ. Matemática 3º Ano - 3º Bimestre / Plano de Trabalho. Geometria Analítica. Tarefa 2
 Fundação CECIERJ/ Consórcio CEDERJ Matemática 3º Ano - 3º Bimestre / 2014 Plano de Trabalho Geometria Analítica Tarefa 2 Cursista: Jocimar de Avila Tutora: Danúbia 1 S u m á r i o Introdução.....................................
Fundação CECIERJ/ Consórcio CEDERJ Matemática 3º Ano - 3º Bimestre / 2014 Plano de Trabalho Geometria Analítica Tarefa 2 Cursista: Jocimar de Avila Tutora: Danúbia 1 S u m á r i o Introdução.....................................
A B C A 1 B 1 C 1 A 2 B 2 C 2 é zero (exceto o caso em que as tres retas são paralelas).
 MAT 105- Lista de Exercícios 1. Prolongue o segmento com extremos em (1, -5) e (3, 1) de um comprimento de (10) unidades. Determine as coordenadas dos novos extremos. 2. Determine o centro e o raio da
MAT 105- Lista de Exercícios 1. Prolongue o segmento com extremos em (1, -5) e (3, 1) de um comprimento de (10) unidades. Determine as coordenadas dos novos extremos. 2. Determine o centro e o raio da
ELIPSE. Figura 1: Desenho de uma elipse no plano euclidiano (à esquerda). Desenho de uma elipse no plano cartesiano (à direita).
 QUÁDRICAS/CÔNICAS - Cálculo II MAT 147 FEAUSP Segundo semestre de 2018 Professor Oswaldo Rio Branco de Oliveira [ Veja também http://www.ime.usp.br/~oliveira/ele-conicas.pdf] No plano euclidiano consideremos
QUÁDRICAS/CÔNICAS - Cálculo II MAT 147 FEAUSP Segundo semestre de 2018 Professor Oswaldo Rio Branco de Oliveira [ Veja também http://www.ime.usp.br/~oliveira/ele-conicas.pdf] No plano euclidiano consideremos
1 Geometria Analítica Plana
 UNIVERSIDADE ESTADUAL DO PARANÁ CAMPUS DE CAMPO MOURÃO Curso: Matemática, 1º ano Disciplina: Geometria Analítica e Álgebra Linear Professora: Gislaine Aparecida Periçaro 1 Geometria Analítica Plana A Geometria
UNIVERSIDADE ESTADUAL DO PARANÁ CAMPUS DE CAMPO MOURÃO Curso: Matemática, 1º ano Disciplina: Geometria Analítica e Álgebra Linear Professora: Gislaine Aparecida Periçaro 1 Geometria Analítica Plana A Geometria
Nome: nº Professor(a): UBERLAN / CRISTIANA Série: 3ª EM Turmas: 3301 / 3302 Data: / /2013
 Nome: nº Professor(a): UBERLAN / CRISTIANA Série: 3ª EM Turmas: 3301 / 3302 Data: / /2013 Sem limite para crescer Bateria de Exercícios de Matemática II 1) A área do triângulo, cujos vértices são (1, 2),
Nome: nº Professor(a): UBERLAN / CRISTIANA Série: 3ª EM Turmas: 3301 / 3302 Data: / /2013 Sem limite para crescer Bateria de Exercícios de Matemática II 1) A área do triângulo, cujos vértices são (1, 2),
UNIVERSIDADE FEDERAL DE PERNAMBUCO
 CÁLCULO L1 NOTAS DA QUINTA AULA UNIVERSIDADE FEDERAL DE PERNAMBUCO Resumo. Iniciamos a aula definindo as funções trigonométricas e estabelecendo algumas de suas propriedades básicas. A seguir, calcularemos
CÁLCULO L1 NOTAS DA QUINTA AULA UNIVERSIDADE FEDERAL DE PERNAMBUCO Resumo. Iniciamos a aula definindo as funções trigonométricas e estabelecendo algumas de suas propriedades básicas. A seguir, calcularemos
Matemática 2 Módulo 9
 Matemática Módulo 9 GEOMETRIA ANALÍTICA VI COMENTÁRIOS ATIVIDADES PARA SALA. Se duas circunferências são concêntricas, então os seus centros são coincidentes. Temos a circunferência λ : x + y 4x y + =
Matemática Módulo 9 GEOMETRIA ANALÍTICA VI COMENTÁRIOS ATIVIDADES PARA SALA. Se duas circunferências são concêntricas, então os seus centros são coincidentes. Temos a circunferência λ : x + y 4x y + =
Resolução das Questões Discursivas
 COMISSÃO PERMANENTE DE SELEÇÃO COPESE PRÓ-REITORIA DE GRADUAÇÃO PROGRAD CONCURSO PISM III - TRIÊNIO 008-010 Prova de Matemática Resolução das Questões Discursivas São apresentadas abaixo possíveis soluções
COMISSÃO PERMANENTE DE SELEÇÃO COPESE PRÓ-REITORIA DE GRADUAÇÃO PROGRAD CONCURSO PISM III - TRIÊNIO 008-010 Prova de Matemática Resolução das Questões Discursivas São apresentadas abaixo possíveis soluções
