x As IyUPXODVGHGLIHUHQFLDomRQXPpULFD podem ser obtidas por: x
|
|
|
- Felícia Maria das Neves Mota Aranha
- 8 Há anos
- Visualizações:
Transcrição
1 &DStWXOR±'LIHUHQFLDomRH,QWHJUDomR1XPpULFDV > 'LIHUHQFLDomR 1XPpULFD Por vezes é necessário obterydoruhvgdvghulydgdvde uma função VHP UHFRUUHUjUHVSHFWLYDH[SUHVVmRDQDOtWLFD, por esta não ser conhecida ou por ser demasiado complicada. As IyUPXODVGHGLIHUHQFLDomRQXPpULFD podem ser obtidas por: polinómios de Taylor polinómios interpoladores de Lagrange Å $SUR[LPDomR GD SULPHLUD GHULYDGD Considere-se FRQKHFLGRV os YDORUHVGDIXQomRHPQyV [ Lí, [ L e [ L respectivamente, I [ Lí I[ L e I[ L Considere-se ainda que o HVSDoDPHQWR entre nós consecutivos é FRQVWDQWH de valor K ou seja, K [ L í[ Lí [ L í[ L. Com base nestes valores, vamos deduzir WUrVIyUPXODV.
2 Fórmula de GLIHUHQoDILQLWDSURJUHVVLYD Fórmula de GLIHUHQoDILQLWDUHJUHVVLYD Fórmula de GLIHUHQoDILQLWDFHQWUDGD
3 'HGXomR GD IyUPXOD GH GLIHUHQoD ILQLWD SURJUHVVLYD D SDUWLU GR SROLQyPLR GH 7D\ORU Consideremos o SROLQyPLRGH7D\ORUGHJUDX centrado em [ L, com resto, para algum Calculando em [ [ L e para K [ L í[ L para algum donde, para algum ou seja, com HUUR dado por, para algum
4 Portanto, VHD GHULYDGDGDIXQomRIRUOLPLWDGD, então D GLIHUHQoDILQLWD SURJUHVVLYDFRQYHUJH para o valor eacto da derivada FRP HUURGDRUGHPGH K. Como o erro é OLQHDU em K, diz-se que a fórmula da diferença progressiva é uma IyUPXODGHSULPHLUDRUGHP. 'HGXomR GD IyUPXOD GH GLIHUHQoD ILQLWD SURJUHVVLYD D SDUWLU GR SROLQyPLR LQWHUSRODGRU GH /DJUDQJH Considerando o SROLQyPLRLQWHUSRODGRUGH/DJUDQJH para os dois pontos [ L I[ L e [ L I[ L, a derivada desta epressão é uma diferença dividida de 1ª ordem, e daqui obtemos a DSUR[LPDomR, A epressão do erro poderia também ser determinada com base no erro GH LQWHUSRODomR.
5 H[HUFtFLR Deduza a fórmula de GLIHUHQoDILQLWDUHJUHVVLYD, a partir do polinómio de Taylor e a partir do polinómio interpolador de Lagrange. 'HGXomR GD IyUPXOD GH GLIHUHQoD ILQLWD FHQWUDGD D SDUWLU GR SROLQyPLR GH 7D\ORU Consideremos o SROLQyPLRGH7D\ORUGHJUDX centrado em [ L, com resto, para algum Calculando em [ [ L eem [ [ L e para K [ L í[ L para algum para algum
6 subtraindo as duas igualdades e assumindo que a terceira derivada é contínua em [ [ L [ L ], temos, para algum ou seja, com HUUR dado por, 6HD GHULYDGDGDIXQomRIRUOLPLWDGD, então D GLIHUHQoDILQLWDFHQWUDGD FRQYHUJH para o valor eacto da derivada FRP HUURGDRUGHPGH K. Como o erro é TXDGUiWLFR em K, diz-se que a fórmula da diferença centrada tem uma SUHFLVmRGHVHJXQGDRUGHP. H[HUFtFLR Deduza a fórmula de GLIHUHQoDILQLWDFHQWUDGD, a partir do polinómio interpolador de Lagrange, FRQVLGHUDQGRWUrVSRQWRV. Por esta razão, a fórmula é conhecida por IyUPXODGRVSRQWRV, embora I[ L não figure eplicitamente.
7 Å $SUR[LPDomR GD VHJXQGD GHULYDGD Considere-se FRQKHFLGRV os YDORUHVGDIXQomRHPQyV [ Lí, [ L e [ L respectivamente, I [ Lí I[ L e I[ L e que o HVSDoDPHQWR entre nós consecutivos é FRQVWDQWH de valor K. Considere-se o SROLQyPLRGH7D\ORUGHJUDX centrado em [ L, com resto, calculado em [ [ L eem [ [ L para algum para algum Somando as duas igualdades e assumindo que a quarta derivada é contínua em [ [ L [ L ], temos, para algum
8 assim, com HUUR dado por, Para encontrar fórmulas para a WHUFHLUDGHULYDGD e TXDUWDGHULYDGD, procuram-se FRPELQDo}HVOLQHDUHV dos desenvolvimentos de Taylor de I [ Lí I[ Lí I[ L e I[ L em torno de [ L de tal forma que as derivadas de ordem inferior à pretendia se anulem. Å $ LQIOXrQFLD GRV HUURV GH DUUHGRQGDPHQWR Teoricamente, se as derivadas apropriadas da função forem limitadas, a GHULYDGD calculada pelas fórmulas de diferenças finitas FRQYHUJH para o valor eacto de acordo com uma certa SRWrQFLDGRSDUkPHWUR K. Na prática os HUURVGHDUUHGRQGDPHQWR constituem o factor predominante de erro. FRPRH[HPSOR, consideremos a IyUPXODGRVSRQWRV, para algum
9 Supondo que no cálculo de I[ Lí ede I[ L foram cometidos HUURVGH DUUHGRQGDPHQWR, então o HUURWRWDO cometido no FiOFXORGDGHULYDGD é, HUURGHDUUHGRQGDPHQWR LQYHUVDPHQWH proporcional a K HUURGHWUXQFDWXUD GLUHFWDPHQWH proporcional a K Portanto, tentar FRQWURODURHUURWRWDO em função de K é uma tarefa delicada, dependente de GRLVIDFWRUHVFRQWUDGLWyULRV. Enquanto que o erro de truncatura é menor para valores pequenos de K, esse HIHLWRpGHVWUXtGR pelo crescimento do erro de arredondamento. É assim vital tentar encontrar um YDORUGHHTXLOtEULR para K, o que naturalmente também depende do valor de [ considerado.
10 XPH[HPSOR YHU A figura representa o comportamento do HUURWRWDO, em função de K, no cálculo da derivada de I[ [ nos pontos [, [ e [ usando a IyUPXODGHGLIHUHQoDILQLWDSURJUHVVLYD( para os 3 valores de [ ) ea IyUPXODGHGLIHUHQoDILQLWDFHQWUDGD( para [ ) a a HUURVGHDUUHGRQGDPHQWR HUURV GHWUXQFDWXUD QRWDURVYDORUHVGH HTXLOtEULRSDUDK
11 Alguns resultados do cálculo da derivada de I[ [ no ponto [ para a IyUPXODGHGLIHUHQoDILQLWDFHQWUDGD. K [K ±[K K HUUR Desde K até cerca de K o erro ( de WUXQFDWXUD ) GHFUHVFH. Mas a partir de K o erro ( provocado por DUUHGRQGDPHQWR ) DXPHQWD. Como neste caso a terceira derivada é constante, I [, o HUURGHWUXQFDWXUD é dado por H[ L K, tal como se pode verificar nos primeiros valores de K.
12 Comportamento do YDORUDEVROXWRdo HUURWRWDO para K desde até : Valores absolutosdo HUURWRWDO e do HUURGHWUXQFDWXUD, para K de até :
13 >,QWHJUDomR 1XPpULFD Por vezes é necessário recorrer a PpWRGRVDSUR[LPDGRV para calcular o valor do LQWHJUDOGHXPDIXQomRQXPLQWHUYDOR, porque: a H[SUHVVmRDQDOtWLFDda função não é conhecida ( função dada por tabelas ou obtida por medições de grandezas físicas ) a epressão analítica da função é conhecida mas a SULPLWLYD não. o SUREOHPD: Calcular um YDORUDSUR[LPDGRde, onde I é integrável em [DE] a VROXomR: Aproimar I por RXWUDIXQomR J cujo integral é fácil de calcular. o HUUR cometido: porque a integração é um RSHUDGRUOLQHDU. Assim, a aproimação do integral será tanto melhor quanto PHOKRU a função J DSUR[LPDU I no intervalo [DE]. os SROLQyPLRV são funções fáceis de integrar...
14 Å )yupxodv GH 1HZWRQ&RWHV Consideremos a )yupxodgh/djudqjhpara o SROLQyPLR S Q de grau Qque interpola a função I nos nós distintos [ [ [ Q : onde / L éo SROLQyPLRGH/DJUDQJH associado ao nó [ L. Assim, e fazendo obtemos a UHJUDGHLQWHJUDomR ou IyUPXODGHTXDGUDWXUD: que nos permite DSUR[LPDURLQWHJUDO da função I, Os $ L chamam-se FRHILFLHQWHV ou SHVRV da regra.
15 Consoante o valor de Q ea localização dos nós no intervalo [DE] obtêm-se diferentes UHJUDVGHLQWHJUDomR. SROLQyPLRLQWHUSRODGRUHP QyV SROLQyPLRLQWHUSRODGRUHP QyV Uma regra de integração diz-se de JUDXGHH[DFWLGmRQ se LQWHJUDUH[DFWDPHQWH WRGRVRVSROLQyPLRVGHJUDX Q e eistir, pelo menos, um polinómio de grau Q que não é integrado eactamente. Assim, toda a regra de integração que resulte da aproimação por um polinómio em Q nós ( polinómio interpolador de grau Q ) tem grau de eactidão Q. 5HJUD GR 7UDSp]LR Seja S o polinómio de grau 1 interpolador de I nos nós D e E, na IRUPDGH1HZWRQ,
16 integrando, ou seja, e assim obtemos a UHJUDWRWUDSp]LR : por ser afinal a epressão da área de um trapézio. O JUDXGHH[DFWLGmR desta fórmula é.
17 5HJUD GH 6LPSVRQ Seja S o polinómio de grau interpolador de I nos nós D, F DE e E, na IRUPDGH1HZWRQ, integrando, e assim obtemos a UHJUDGH6LPSVRQ : Pela construção anterior, o JUDXGHH[DFWLGmR desta fórmula é pelo menos 2, mas veremos que de facto é. Ou seja, a regra de Simpson dá resultados eactos para polinómios de grau.
18 5HJUD GRV WUrV RLWDYRV 6LPSVRQ Dividindo o intervalo [DE] em SDUWHVLJXDLV (em vez de 2) e considerando LQWHUSRODomRF~ELFD (em vez de quadrática) não é difícil deduzir a UHJUDGRV De forma análoga se podem definir mais regras de integração, baseadas na LQWHUSRODomRSRUXPSROLQyPLR de grau cada vez maior, não sendo contudo de garantir que os resultados obtidos sejam melhores. $ IDPtOLD GH UHJUDV GH 1HZWRQ&RWHV Todas as fórmulas deste tipo podem ser deduzidas de forma sistemática: Cada uma é baseada na LQWHUSRODomR da função integranda SRUXPSROLQyPLR, de grau Q, em Q SRQWRVHTXLGLVWDQWHV no intervalo de integração, com e toda a regra tem a forma:
19 com, e onde D QL D L Å (UURV GDV IyUPXODV GH 1HZWRQ&RWHV (UUR GD 5HJUD GR 7UDSp]LR WHRUHPD Seja I & ([DE]). Então: ( O erro depende da VHJXQGDGHULYDGD, o que vem confirmar que o JUDXGH H[DFWLGmR da Regra do Trapézio é )
20 GHPRQVWUDomR Sendo S Q o SROLQyPLR de grau QTXHLQWHUSROD I & Q ([DE]) nos nós distintos [ [ [ Q, então, Como neste caso se trata de um polinómio de JUDX, interpolador nos pontos D e E, Falta assim demonstrar que, HUUR de integração da 5HJUDGR7UDSp]LR Para isso relembremos o, 7HRUHPDGR9DORU0pGLR3HVDGRSDUD,QWHJUDLV: Se I & ([DE]) e J é integrável em [DE] e J[ QmRPXGDGHVLQDO em [a, b], então eiste um número F, D < F < E, tal que:
21 Como [D[E não muda de sinal em [a, b] e I é contínua, e porque, fica provado que, (UUR GD 5HJUD GH 6LPSVRQ De modo análogo se prova que, para I & ([DE]), ou seja, a epressão do HUUR de integração da 5HJUDGH6LPSVRQ, ( Como este erro depende da TXDUWDGHULYDGD, vemos que o JUDXGH H[DFWLGmR da Regra de Simpson é efectivamente )
22 7DEHOD GH HUURV GD IDPtOLD GH UHJUDV GH 1HZWRQ&RWHV onde K EDQ Cada regra de Newton-Cotes é baseada na LQWHUSRODomR da função integranda SRUXPSROLQyPLR, de grau Q, em Q SRQWRVHTXLGLVWDQWHV no intervalo de integração. Se Q é tpsdu, a regra tem JUDXGHH[DFWLGmRQ ese Q é SDU, a regra tem JUDXGHH[DFWLGmRQ Contudo, devido a efeitos de FDQFHODPHQWRVXEWUDFWLYR, regras de grau mais elevado não produzem melhores resultados. Como as epressões dos erros dependem de SRWrQFLDVGHK, a solução consiste em subdividir o intervalo de integração em VXELQWHUYDORVPHQRUHV.
23 Å 5HJUDV &RPSRVWDV 5HJUD GR 7UDSp]LR &RPSRVWD Defina-se a SDUWLomR de [DE] em 1 VXELQWHUYDORVGHLJXDODPSOLWXGH, nos pontos [ D[ [ Q E, onde [ L = D + LK com K =(EíD1. Então, Aplicando a UHJUDGRWUDSp]LRa cada um dos 1 integrais, somando, e considerando I L I[ L obtém-se a 5HJUDGRV7UDSp]LRV&RPSRVWD :
24 (UUR GD 5HJUD GRV 7UDSp]LRV &RPSRVWD WHRUHPD Seja I & ([DE]) e [ L = D + LK com K =(EíD1. Então, GHPRQVWUDomR Tomando, aplicando a regra do trapézio a cada um dos subintervalos [[ Lí [ L ] : e somando temos,
25 Seja, pelo WHRUHPDGRYDORUPpGLRSDUDVRPDVILQLWDV de valores de uma função, donde obtemos o (UURGH7UXQFDWXUDGD5HJUDGRV7UDSp]LRV&RPSRVWD, porque K E±D1 Para o caso particular de 1 ( ou seja K E±D ) temos a fórmula do erro para a regra do trapézio simples. O factor K indica que o erro de truncatura depende ( quadraticamente ) da amplitude dos subintervalos considerados. Do ponto de vista prático, esta fórmula não é muito vantajosa...
26 (VWLPDWLYD SDUD R (UUR GD 5HJUD GRV 7UDSp]LRV &RPSRVWD Consideremos apenas o caso de o Q~PHURGHVXELQWHUYDORVser SDU, 1 N. Se I & ([DE]) calculemos, uma aproimação, 7 (K) para,(i) com 1 subintervalos, e uma aproimação, 7 (2K) para,(i) com 1 subintervalos, Onde, ese I QmRYDULDUPXLWR em (DE) então e Subtraindo as duas fórmulas acima,
27 donde, SRUH[HPSOR Pelas UHJUDVGRVWUDSp]LRV, calculemos aproimações de, Com se utilizarmos a regra do trapézio simples, (, = ) para 1 =2 e K = S /2, para 1 =4 e K = S /4,
28 para 1 =8 e K = S /8, = Continuando, obteríamos: 1, 1 Analisando os YDORUHVUHDLVGRVHUURV, 1 (1 (1(1 podemos verificar que efectivamente, (1ž (1
29 Calculando _, 1 ±, 1 _ obtemos uma aproimação de (1 : 5HJUD GH 6LPSVRQ &RPSRVWD Defina-se a SDUWLomR de [DE] em 1 VXELQWHUYDORVGHLJXDODPSOLWXGH, nos pontos [ D[ [ Q E, onde [ L = D + LK com K =(EíD1. Então, Aplicando a UHJUDGH6LPSVRQa cada SDUGHVXELQWHUYDORV consecutivos,
30 somando, e considerando I L I[ L obtém-se a 5HJUDGH6LPSVRQ&RPSRVWD: (UUR GD 5HJUD GH 6LPSVRQ &RPSRVWD WHRUHPD Seja I & ([DE]) e [ L = D + LK com K =(EíD1 e 1 par. Então GHPRQVWUDomR( DQiORJDjDQWHULRU )
31 (VWLPDWLYD SDUD R (UUR GD 5HJUD GH 6LPSVRQ &RPSRVWD Consideremos apenas o caso de o Q~PHURGHVXELQWHUYDORVser P~OWLSORGH, 1 N. Se I & ([DE]) calculemos, uma aproimação, 6 (K) para,(i) com 1 subintervalos, e uma aproimação, 6 (2K) para,(i) com 1 (=N ) subintervalos, Se I QmRYDULDUPXLWR em (DE) então, pela fórmula do erro, pode verificar-se que, Subtraindo as duas fórmulas acima, donde,
32 SDUDRPHVPRH[HPSOR Pelas UHJUDVGH6LPSVRQ, calculemos aproimações de, (, = ) Comecemos por considerar a regra de Simpson para 1 =2 e K = S /2, para 1 =4 e K = S /4, = Continuando, obteríamos: 1, 1
33 Analisando os YDORUHVUHDLVGRVHUURV, 1 (1 (1(1 podemos verificar que efectivamente, (1ž (1 Calculando _, 1 ±, 1 _ obtemos uma aproimação de (1 : Comparando com os resultados obtido para a Regra dos Trapézios, verificamos que 5HJUDGH6LPSVRQ é computacionalmente PHOKRU. É possível utilizar regras de integração obtidas da utilização de polinómios que LQWHUSRODP não só a IXQomRLQWHJUDQGD mas também as suas GHULYDGDV.
34 Å )yupxodv GH LQWHJUDomR FRP YDORUHV GDV GHULYDGDV GD IXQomR LQWHJUDQGD Como caso particular considere-se o 3ROLQyPLR&~ELFRGH+HUPLWHinterpolador de I e de I em D e E, na forma de Newton, o HUURGHLQWHUSRODomR é, e portanto, Se calcularmos o integral de + [ em [DE],com K EíD :
35 verificamos que, UHJUDGRWUDSp]LR IDFWRUGHFRUUHFomR Justifica-se desta forma a designação 5HJUDGR7UDSp]LR&RUULJLGDpara a fórmula: Para determinar o (UURGD5HJUDGR7UDSp]LR&RUULJLGDcalculemos, que, recorrendo ao 7HRUHPDGR9DORU0pGLR3HVDGRSDUD,QWHJUDLV, e portanto para algum
36 5HJUD GRV 7UDSp]LRV &RUULJLGD &RPSRVWD Considere-se I & ([DE]) e a SDUWLomR de [DE] em 1 subintervalos de igual amplitude, nos pontos [ D[ [ Q E, onde [ L = D + LK com K =(EíD1. Então, Aplicando a regra dos trapézios FRUULJLGD a cada um dos integrais do segundo membro, e somando,
37 obtém-se a fórmula dos 7UDSp]LRV&RUULJLGD&RPSRVWD, e respectivo HUUR. SDUDRPHVPRH[HPSOR Pelas regras dos 7UDSp]LRV simples e 7UDSp]LRV&RUULJLGD ( ambas &RPSRVWDV ) 1, 7 ( 7, 7& ( 7& verificamos que ( 7& 1ž ( 7 1
38 Å )yupxodv GH *DXVV/HJHQGUH 4XDGUDWXUD GH *DXVV FRP 3ROLQyPLRV GH /HJHQGUH Cada regra de integração da família Newton-Cotes, é baseada na interpolação polinomial da função integranda em Q SRQWRV HTXLGLVWDQWHVe IL[RV [ L no intervalo de integração. Os Q FRHILFLHQWHV $ L são determinados de modo a que a integração seja H[DFWD para polinómios de JUDX Q. Na 4XDGUDWXUDGH*DXVV, os Q pontos [ L e mais os Q coeficientes $ L formam um conjunto de Q SDUkPHWURV, que serão determinados de modo a que a integração seja H[DFWD para polinómios de JUDX 2Q. No que se segue, a integração será efectuada no LQWHUYDOR []. Para o caso geral, basta uma PXGDQoDGHYDULiYHO, por forma a obter, ( W í [ De W [ E )
39 )yupxod GH *DXVV/HJHQGUH SDUD SRQWRV Neste caso (Q=) temos, onde $, $, [, [ são Q= LQFyJQLWDV a determinar, de modo a que a integração seja H[DFWD para polinómios de JUDX 2Q. No espaço P 3 dos SROLQyPLRVGHJUDXDWp consideremos a EDVH (, [, [, [ ). Como o operador integração é OLQHDU, a integração deverá ser H[DFWD para as funções da base:, [, [ e [. Assim, basta calcular: donde obtemos FRQGLo}HV. A solução do VLVWHPD fornece os valores dos SDUkPHWURV procurados: $ = $ =1 [ = [ =
40 Assim, a IyUPXODGH*DXVV/HJHQGUHSDUDGRLVSRQWRV, consiste apenas na soma dos valores da função em dois pontos, e calcula uma aproimação do integral com JUDXGHH[DFWLGmR igual awurv. Note-se que se trata efectivamente da iuhdghxpwudsp]lr, no intervalo [], definido pelos valores de I[em [ = e [ = UHJUDGRWUDSp]LR IyUPXODGH*DXVVSDUDSRQWRV Apesar da sua simplicidade, com a fórmula de Gauss-Legendre de GRLVSRQWRV a LQWHJUDomRpH[DFWD para todos os SROLQyPLRVGHJUDXH. Podemos verificar que o mesmo já não acontece para polinómios de grau 4. Para I[ [, mas
41 SDUDRPHVPRH[HPSOR Pela IyUPXODGH*DXVV/HJHQGUHGHGRLVSRQWRV calculemos uma aproimação de, (, = ) Efectuando uma mudança de variável, de forma a obter [ ± [,] I[ = ( =
42 Prova-se que, se I & ([]), o HUURGHWUXQFDWXUD da IyUPXODGH*DXVV /HJHQGUHGHGRLVSRQWRV é dado por, )yupxodv GH *DXVV/HJHQGUH SDUD Q SRQWRV Se I & ([]) podemos deduzir de modo análogo a IyUPXODGH*DXVV /HJHQGUHSDUDWUrVSRQWRV, onde, Verifique que esta fórmula tem JUDXGHH[DFWLGmR igual a. Assim temos,
43 O mesmo procedimento poderia ser aplicado para qualquer valor de Q, eigindo contudo a resolução de um sistema de 2Q equações a 2Q incógnitas. No entanto, é possível mostrar que tanto os QyV [ L como os SHVRV $ L podem ser obtidos a partir dos SROLQyPLRVGH/HJHQGUH. Cada SROLQyPLRGH/HJHQGUH 3 Q [ tem Q UDt]HV no intervalo [í,] e essas raízes são eactamente os QyV das regras de quadratura gaussiana. Sob o ponto de vista prático são utilizadas WDEHODV onde, em função do Q~PHURGH SRQWRV (Q) considerado, são dados os valores dos QyV [ L edos SHVRV $ L,com L Q. Q [ L $ L (UUR
44 SDUDRPHVPRH[HPSOR Pelas IyUPXODVGH*DXVV/HJHQGUH calculemos sucessivas aproimações de, (, = ) Q, Q ( Q Verificamos que o HUURGHFUHVFHPXLWRUDSLGDPHQWH quando o número de pontos de integração aumenta. Compare com a aplicação das regras anteriores, onde erros da ordem de são apenas obtidos para mais de 1000 pontos.
Como aparecem os erros? Quais os seus efeitos? Como controlar esses efeitos?
 &DStWXOR±5HSUHVHQWDomRGH1~PHURVH(UURV,QWURGXomR Como aparecem os erros? Quais os seus efeitos? Como controlar esses efeitos? 7LSRVGH(UURV Erros inerentes à matematização do fenómeno físico: os sistemas
&DStWXOR±5HSUHVHQWDomRGH1~PHURVH(UURV,QWURGXomR Como aparecem os erros? Quais os seus efeitos? Como controlar esses efeitos? 7LSRVGH(UURV Erros inerentes à matematização do fenómeno físico: os sistemas
Notas sobre a Fórmula de Taylor e o estudo de extremos
 Notas sobre a Fórmula de Taylor e o estudo de etremos O Teorema de Taylor estabelece que sob certas condições) uma função pode ser aproimada na proimidade de algum ponto dado) por um polinómio, de modo
Notas sobre a Fórmula de Taylor e o estudo de etremos O Teorema de Taylor estabelece que sob certas condições) uma função pode ser aproimada na proimidade de algum ponto dado) por um polinómio, de modo
Métodos Numéricos e Estatísticos Parte I-Métodos Numéricos Teoria de Erros
 Métodos Numéricos e Estatísticos Parte I-Métodos Numéricos Lic. Eng. Biomédica e Bioengenharia-2009/2010 O que é a Análise Numérica? Ramo da Matemática dedicado ao estudo e desenvolvimento de métodos (métodos
Métodos Numéricos e Estatísticos Parte I-Métodos Numéricos Lic. Eng. Biomédica e Bioengenharia-2009/2010 O que é a Análise Numérica? Ramo da Matemática dedicado ao estudo e desenvolvimento de métodos (métodos
CAP. I ERROS EM CÁLCULO NUMÉRICO
 CAP. I ERROS EM CÁLCULO NUMÉRICO 0. Introdução Por método numérico entende-se um método para calcular a solução de um problema realizando apenas uma sequência finita de operações aritméticas. A obtenção
CAP. I ERROS EM CÁLCULO NUMÉRICO 0. Introdução Por método numérico entende-se um método para calcular a solução de um problema realizando apenas uma sequência finita de operações aritméticas. A obtenção
[ \ x Recordemos o caso mais simples de um VLVWHPD de duas HTXDo}HVOLQHDUHV nas duas LQFyJQLWDV [ e \.
 &DStWXOR±6LVWHPDVGH(TXDo}HV/LQHDUHV1 &DStWXOR±6LVWHPDVGH(TXDo}HV/LQHDUHV Å 1Ro}HV *HUDLV Recordemos o caso mais simples de um VLVWHPD de duas HTXDo}HVOLQHDUHV nas duas LQFyJQLWDV [ e \. [\ [\ É fácil verificar
&DStWXOR±6LVWHPDVGH(TXDo}HV/LQHDUHV1 &DStWXOR±6LVWHPDVGH(TXDo}HV/LQHDUHV Å 1Ro}HV *HUDLV Recordemos o caso mais simples de um VLVWHPD de duas HTXDo}HVOLQHDUHV nas duas LQFyJQLWDV [ e \. [\ [\ É fácil verificar
x As VpULHVGHSRWrQFLDV são um caso particularmente importante das séries de funções, com inúmeras aplicações tanto teóricas como práticas.
 Å 6pULHV GH SRWrQFLDV As VpULHVGHSRWrQFLDV são um caso particularmente importante das séries de funções, com inúmeras aplicações tanto teóricas como práticas. Um eemplo típico é a série, O cálculo do valor
Å 6pULHV GH SRWrQFLDV As VpULHVGHSRWrQFLDV são um caso particularmente importante das séries de funções, com inúmeras aplicações tanto teóricas como práticas. Um eemplo típico é a série, O cálculo do valor
Licenciatura em Engenharia Electrotécnica e de Computadores 1998/99. Erros
 Licenciatura em Engenharia Electrotécnica e de Computadores Análise Numérica 1998/99 Erros Objectivos: Arredondar um número para n dígitos significativos. Determinar os erros máximos absoluto e relativo
Licenciatura em Engenharia Electrotécnica e de Computadores Análise Numérica 1998/99 Erros Objectivos: Arredondar um número para n dígitos significativos. Determinar os erros máximos absoluto e relativo
M : ( ( é um LVRPRUILVPR M -1 : ( ( também é um LVRPRUILVPR.
 &DStWXOR±$SOLFDo}HV/LQHDUHV47 Å (VSDoRV,VRPRUIRV Sejam ( e ( dois espaços vectoriais sobre. Dizemos que ( e ( são LVRPRUIRV se H[LVWLUXPLVRPRUILVPR M : ( ( e escrevemos, (! ( Por eemplo, o espaço dos vectores
&DStWXOR±$SOLFDo}HV/LQHDUHV47 Å (VSDoRV,VRPRUIRV Sejam ( e ( dois espaços vectoriais sobre. Dizemos que ( e ( são LVRPRUIRV se H[LVWLUXPLVRPRUILVPR M : ( ( e escrevemos, (! ( Por eemplo, o espaço dos vectores
CÁLCULO DE ZEROS DE FUNÇÕES REAIS
 15 CÁLCULO DE ZEROS DE FUNÇÕES REAIS Um dos problemas que ocorrem mais frequentemente em trabalhos científicos é calcular as raízes de equações da forma: f() = 0. A função f() pode ser um polinômio em
15 CÁLCULO DE ZEROS DE FUNÇÕES REAIS Um dos problemas que ocorrem mais frequentemente em trabalhos científicos é calcular as raízes de equações da forma: f() = 0. A função f() pode ser um polinômio em
2004/2005 PROBLEMAS. y 0.78 2.04 3.71 4.11 3.89. f(x) dx.
 Licenciatura em Engenharia Electrotécnica e de Computadores Análise Numérica /5 Integração Numérica PROBLEMAS Dados os seguintes pontos de uma função y = f(x) x y.78..7..89 determine um valor aproximado
Licenciatura em Engenharia Electrotécnica e de Computadores Análise Numérica /5 Integração Numérica PROBLEMAS Dados os seguintes pontos de uma função y = f(x) x y.78..7..89 determine um valor aproximado
9. Derivadas de ordem superior
 9. Derivadas de ordem superior Se uma função f for derivável, então f é chamada a derivada primeira de f (ou de ordem 1). Se a derivada de f eistir, então ela será chamada derivada segunda de f (ou de
9. Derivadas de ordem superior Se uma função f for derivável, então f é chamada a derivada primeira de f (ou de ordem 1). Se a derivada de f eistir, então ela será chamada derivada segunda de f (ou de
Equações Diferenciais Ordinárias
 Equações Diferenciais Ordinárias Uma equação diferencial é uma equação que relaciona uma ou mais funções (desconhecidas com uma ou mais das suas derivadas. Eemplos: ( t dt ( t, u t d u ( cos( ( t d u +
Equações Diferenciais Ordinárias Uma equação diferencial é uma equação que relaciona uma ou mais funções (desconhecidas com uma ou mais das suas derivadas. Eemplos: ( t dt ( t, u t d u ( cos( ( t d u +
Explorações de alunos
 A partir dos exemplos sugeridos e explorados pelos alunos pretende-se que possam conjecturar que, dadas duas funções reais de variável real f e g, o domínio da função quociente pode ser dado por: f f g
A partir dos exemplos sugeridos e explorados pelos alunos pretende-se que possam conjecturar que, dadas duas funções reais de variável real f e g, o domínio da função quociente pode ser dado por: f f g
Erros. Número Aproximado. Erros Absolutos erelativos. Erro Absoluto
 Erros Nenhum resultado obtido através de cálculos eletrônicos ou métodos numéricos tem valor se não tivermos conhecimento e controle sobre os possíveis erros envolvidos no processo. A análise dos resultados
Erros Nenhum resultado obtido através de cálculos eletrônicos ou métodos numéricos tem valor se não tivermos conhecimento e controle sobre os possíveis erros envolvidos no processo. A análise dos resultados
Aula 10. Integração Numérica
 CÁLCULO NUMÉRICO Aula Integração Numérica Integração Numérica Cálculo Numérico 3/4 Integração Numérica Em determinadas situações, integrais são difíceis, ou mesmo impossíveis de se resolver analiticamente.
CÁLCULO NUMÉRICO Aula Integração Numérica Integração Numérica Cálculo Numérico 3/4 Integração Numérica Em determinadas situações, integrais são difíceis, ou mesmo impossíveis de se resolver analiticamente.
A equação do 2º grau
 A UA UL LA A equação do 2º grau Introdução Freqüentemente, ao equacionarmos um problema, obtemos uma equação na qual a incógnita aparece elevada ao quadrado. Estas são as chamadas equações do 2º grau.
A UA UL LA A equação do 2º grau Introdução Freqüentemente, ao equacionarmos um problema, obtemos uma equação na qual a incógnita aparece elevada ao quadrado. Estas são as chamadas equações do 2º grau.
Aula 4 Estatística Conceitos básicos
 Aula 4 Estatística Conceitos básicos Plano de Aula Amostra e universo Média Variância / desvio-padrão / erro-padrão Intervalo de confiança Teste de hipótese Amostra e Universo A estatística nos ajuda a
Aula 4 Estatística Conceitos básicos Plano de Aula Amostra e universo Média Variância / desvio-padrão / erro-padrão Intervalo de confiança Teste de hipótese Amostra e Universo A estatística nos ajuda a
Karine Nayara F. Valle. Métodos Numéricos de Euler e Runge-Kutta
 Karine Nayara F. Valle Métodos Numéricos de Euler e Runge-Kutta Professor Orientador: Alberto Berly Sarmiento Vera Belo Horizonte 2012 Karine Nayara F. Valle Métodos Numéricos de Euler e Runge-Kutta Monografia
Karine Nayara F. Valle Métodos Numéricos de Euler e Runge-Kutta Professor Orientador: Alberto Berly Sarmiento Vera Belo Horizonte 2012 Karine Nayara F. Valle Métodos Numéricos de Euler e Runge-Kutta Monografia
Alguns apontamentos da história da Análise Numérica
 Análise Numérica 1 Âmbito da Análise Numérica Determinar boas soluções aproximadas num tempo computacional razoável? Slide 1 Porquê? Porque em muitos problemas matemáticos e respectivas aplicações práticas
Análise Numérica 1 Âmbito da Análise Numérica Determinar boas soluções aproximadas num tempo computacional razoável? Slide 1 Porquê? Porque em muitos problemas matemáticos e respectivas aplicações práticas
Estudo do Sinal de uma Função
 Capítulo 1 Estudo do Sinal de uma Função 11 Introdução Neste Capítulo discutimos o problema do estudo do sinal de uma função, assunto muitas vezes tratado de forma rápida e supercial nos ensinos básico
Capítulo 1 Estudo do Sinal de uma Função 11 Introdução Neste Capítulo discutimos o problema do estudo do sinal de uma função, assunto muitas vezes tratado de forma rápida e supercial nos ensinos básico
Todos os exercícios sugeridos nesta apostila se referem ao volume 1. MATEMÁTICA I 1 FUNÇÃO DO 1º GRAU
 FUNÇÃO IDENTIDADE... FUNÇÃO LINEAR... FUNÇÃO AFIM... GRÁFICO DA FUNÇÃO DO º GRAU... IMAGEM... COEFICIENTES DA FUNÇÃO AFIM... ZERO DA FUNÇÃO AFIM... 8 FUNÇÕES CRESCENTES OU DECRESCENTES... 9 SINAL DE UMA
FUNÇÃO IDENTIDADE... FUNÇÃO LINEAR... FUNÇÃO AFIM... GRÁFICO DA FUNÇÃO DO º GRAU... IMAGEM... COEFICIENTES DA FUNÇÃO AFIM... ZERO DA FUNÇÃO AFIM... 8 FUNÇÕES CRESCENTES OU DECRESCENTES... 9 SINAL DE UMA
ficha 3 espaços lineares
 Exercícios de Álgebra Linear ficha 3 espaços lineares Exercícios coligidos por Jorge Almeida e Lina Oliveira Departamento de Matemática, Instituto Superior Técnico 2 o semestre 2011/12 3 Notação Sendo
Exercícios de Álgebra Linear ficha 3 espaços lineares Exercícios coligidos por Jorge Almeida e Lina Oliveira Departamento de Matemática, Instituto Superior Técnico 2 o semestre 2011/12 3 Notação Sendo
Só Matemática O seu portal matemático http://www.somatematica.com.br FUNÇÕES
 FUNÇÕES O conceito de função é um dos mais importantes em toda a matemática. O conceito básico de função é o seguinte: toda vez que temos dois conjuntos e algum tipo de associação entre eles, que faça
FUNÇÕES O conceito de função é um dos mais importantes em toda a matemática. O conceito básico de função é o seguinte: toda vez que temos dois conjuntos e algum tipo de associação entre eles, que faça
Faculdade de Engenharia Optimização. Prof. Doutor Engº Jorge Nhambiu
 1 Programação Não Linear Aula 25: Programação Não-Linear - Funções de Uma única variável Mínimo; Mínimo Global; Mínimo Local; Optimização Irrestrita; Condições Óptimas; Método da Bissecção; Método de Newton.
1 Programação Não Linear Aula 25: Programação Não-Linear - Funções de Uma única variável Mínimo; Mínimo Global; Mínimo Local; Optimização Irrestrita; Condições Óptimas; Método da Bissecção; Método de Newton.
AMEI Escolar Matemática 9º Ano Equações do 2º grau
 AMEI Escolar Matemática 9º Ano Equações do 2º grau Operações com polinómios. Casos notáveis da multiplicação de polinómios. Decomposição em factores (revisões) Na escrita de polinómios as letras representam
AMEI Escolar Matemática 9º Ano Equações do 2º grau Operações com polinómios. Casos notáveis da multiplicação de polinómios. Decomposição em factores (revisões) Na escrita de polinómios as letras representam
Numa turma de 26 alunos, o número de raparigas excede em 4 o número de rapazes. Quantos rapazes há nesta turma?
 GUIÃO REVISÕES Equações e Inequações Equações Numa turma de 6 alunos, o número de raparigas ecede em 4 o número de rapazes. Quantos rapazes há nesta turma? O objectivo do problema é determinar o número
GUIÃO REVISÕES Equações e Inequações Equações Numa turma de 6 alunos, o número de raparigas ecede em 4 o número de rapazes. Quantos rapazes há nesta turma? O objectivo do problema é determinar o número
Problemas de Valor Inicial para Equações Diferenciais Ordinárias
 Problemas de Valor Inicial para Equações Diferenciais Ordinárias Carlos Balsa balsa@ipb.pt Departamento de Matemática Escola Superior de Tecnologia e Gestão de Bragança Matemática Aplicada - Mestrados
Problemas de Valor Inicial para Equações Diferenciais Ordinárias Carlos Balsa balsa@ipb.pt Departamento de Matemática Escola Superior de Tecnologia e Gestão de Bragança Matemática Aplicada - Mestrados
Vestibular 2ª Fase Resolução das Questões Discursivas
 COMISSÃO PERMANENTE DE SELEÇÃO COPESE PRÓ-REITORIA DE GRADUAÇÃO PROGRAD CONCURSO VESTIBULAR 010 Prova de Matemática Vestibular ª Fase Resolução das Questões Discursivas São apresentadas abaixo possíveis
COMISSÃO PERMANENTE DE SELEÇÃO COPESE PRÓ-REITORIA DE GRADUAÇÃO PROGRAD CONCURSO VESTIBULAR 010 Prova de Matemática Vestibular ª Fase Resolução das Questões Discursivas São apresentadas abaixo possíveis
Expansão linear e geradores
 Espaços Vectoriais - ALGA - 004/05 4 Expansão linear e geradores Se u ; u ; :::; u n são vectores de um espaço vectorial V; como foi visto atrás, alguns vectores de V são combinação linear de u ; u ; :::;
Espaços Vectoriais - ALGA - 004/05 4 Expansão linear e geradores Se u ; u ; :::; u n são vectores de um espaço vectorial V; como foi visto atrás, alguns vectores de V são combinação linear de u ; u ; :::;
Capítulo 2 - Problemas de Valores Fronteira para Equações Diferenciais Ordinárias
 Capítulo 2 - Problemas de Valores Fronteira para Equações Diferenciais Ordinárias Departamento de Matemática balsa@ipb.pt Mestrados em Engenharia da Construção Métodos de Aproximação em Engenharia 1 o
Capítulo 2 - Problemas de Valores Fronteira para Equações Diferenciais Ordinárias Departamento de Matemática balsa@ipb.pt Mestrados em Engenharia da Construção Métodos de Aproximação em Engenharia 1 o
Universidade Federal de São Carlos Departamento de Matemática 083020 - Curso de Cálculo Numérico - Turma E Resolução da Primeira Prova - 16/04/2008
 Universidade Federal de São Carlos Departamento de Matemática 08300 - Curso de Cálculo Numérico - Turma E Resolução da Primeira Prova - 16/0/008 1. (0 pts.) Considere o sistema de ponto flutuante normalizado
Universidade Federal de São Carlos Departamento de Matemática 08300 - Curso de Cálculo Numérico - Turma E Resolução da Primeira Prova - 16/0/008 1. (0 pts.) Considere o sistema de ponto flutuante normalizado
FUNÇÃO DO 1º GRAU. Vamos iniciar o estudo da função do 1º grau, lembrando o que é uma correspondência:
 FUNÇÃO DO 1º GRAU Vamos iniciar o estudo da função do 1º grau, lembrando o que é uma correspondência: Correspondência: é qualquer conjunto de pares ordenados onde o primeiro elemento pertence ao primeiro
FUNÇÃO DO 1º GRAU Vamos iniciar o estudo da função do 1º grau, lembrando o que é uma correspondência: Correspondência: é qualquer conjunto de pares ordenados onde o primeiro elemento pertence ao primeiro
4.1 Em cada caso use a definição para calcular f 0 (x). (a) f (x) =x 3,x R (b) f (x) =1/x, x 6= 0 (c) f (x) =1/ x, x > 0.
 4. Em cada caso use a definição para calcular f 0 (). (a) f () = 3, R (b) f () =/, 6= 0 (c) f () =/, > 0. 4.2 Mostre que a função f () = /3, R, não é diferenciável em =0. 4.3 Considere a função f : R R
4. Em cada caso use a definição para calcular f 0 (). (a) f () = 3, R (b) f () =/, 6= 0 (c) f () =/, > 0. 4.2 Mostre que a função f () = /3, R, não é diferenciável em =0. 4.3 Considere a função f : R R
(x, y) = (a, b) + t*(c-a, d-b) ou: x = a + t*(c-a) y = b + t*(d-b)
 Equação Vetorial da Reta Dois pontos P e Q, definem um único vetor v = PQ, que representa uma direção. Todo ponto R cuja direção PR seja a mesma de PQ está contido na mesma reta definida pelos pontos P
Equação Vetorial da Reta Dois pontos P e Q, definem um único vetor v = PQ, que representa uma direção. Todo ponto R cuja direção PR seja a mesma de PQ está contido na mesma reta definida pelos pontos P
Material Teórico - Módulo de Divisibilidade. MDC e MMC - Parte 1. Sexto Ano. Prof. Angelo Papa Neto
 Material Teórico - Módulo de Divisibilidade MDC e MMC - Parte 1 Sexto Ano Prof. Angelo Papa Neto 1 Máximo divisor comum Nesta aula, definiremos e estudaremos métodos para calcular o máximo divisor comum
Material Teórico - Módulo de Divisibilidade MDC e MMC - Parte 1 Sexto Ano Prof. Angelo Papa Neto 1 Máximo divisor comum Nesta aula, definiremos e estudaremos métodos para calcular o máximo divisor comum
MATEMÁTICA. Aula 1 Revisão. Prof. Anderson
 MATEMÁTICA Aula 1 Revisão Prof. Anderson Assuntos Equação do 1º grau com uma variável. Sistemas de equações do 1º grau com duas variáveis. Equação do º grau com uma variável. Equação do 1º grau com uma
MATEMÁTICA Aula 1 Revisão Prof. Anderson Assuntos Equação do 1º grau com uma variável. Sistemas de equações do 1º grau com duas variáveis. Equação do º grau com uma variável. Equação do 1º grau com uma
Cálculo Numérico Aula 1: Computação numérica. Tipos de Erros. Aritmética de ponto flutuante
 Cálculo Numérico Aula : Computação numérica. Tipos de Erros. Aritmética de ponto flutuante Computação Numérica - O que é Cálculo Numérico? Cálculo numérico é uma metodologia para resolver problemas matemáticos
Cálculo Numérico Aula : Computação numérica. Tipos de Erros. Aritmética de ponto flutuante Computação Numérica - O que é Cálculo Numérico? Cálculo numérico é uma metodologia para resolver problemas matemáticos
Nível B3 SISTEMAS DE EQUAÇÕES
 Nível B SISTEMAS DE EQUAÇÕES Equações do º grau com duas incógnitas Equação do º grau com duas incógnitas é uma equação onde figuram eactamente duas letras com epoente, por eemplo: -. Uma solução de uma
Nível B SISTEMAS DE EQUAÇÕES Equações do º grau com duas incógnitas Equação do º grau com duas incógnitas é uma equação onde figuram eactamente duas letras com epoente, por eemplo: -. Uma solução de uma
Estudo do Sinal de uma Função
 Capítulo 4 Estudo do Sinal de uma Função 4.1 Introdução Neste Capítulo discutimos o problema do estudo do sinal de uma função, assunto muitas vezes tratado de forma rápida e supercial nos ensinos básico
Capítulo 4 Estudo do Sinal de uma Função 4.1 Introdução Neste Capítulo discutimos o problema do estudo do sinal de uma função, assunto muitas vezes tratado de forma rápida e supercial nos ensinos básico
por séries de potências
 Seção 23: Resolução de equações diferenciais por séries de potências Até este ponto, quando resolvemos equações diferenciais ordinárias, nosso objetivo foi sempre encontrar as soluções expressas por meio
Seção 23: Resolução de equações diferenciais por séries de potências Até este ponto, quando resolvemos equações diferenciais ordinárias, nosso objetivo foi sempre encontrar as soluções expressas por meio
Aritmética Binária e. Bernardo Nunes Gonçalves
 Aritmética Binária e Complemento a Base Bernardo Nunes Gonçalves Sumário Soma e multiplicação binária Subtração e divisão binária Representação com sinal Sinal e magnitude Complemento a base. Adição binária
Aritmética Binária e Complemento a Base Bernardo Nunes Gonçalves Sumário Soma e multiplicação binária Subtração e divisão binária Representação com sinal Sinal e magnitude Complemento a base. Adição binária
Tópico 11. Aula Teórica/Prática: O Método dos Mínimos Quadrados e Linearização de Funções
 Tópico 11. Aula Teórica/Prática: O Método dos Mínimos Quadrados e Linearização de Funções 1. INTRODUÇÃO Ao se obter uma sucessão de pontos experimentais que representados em um gráfico apresentam comportamento
Tópico 11. Aula Teórica/Prática: O Método dos Mínimos Quadrados e Linearização de Funções 1. INTRODUÇÃO Ao se obter uma sucessão de pontos experimentais que representados em um gráfico apresentam comportamento
AS LEIS DE NEWTON PROFESSOR ANDERSON VIEIRA
 CAPÍTULO 1 AS LEIS DE NEWTON PROFESSOR ANDERSON VIEIRA Talvez o conceito físico mais intuitivo que carregamos conosco, seja a noção do que é uma força. Muito embora, formalmente, seja algo bastante complicado
CAPÍTULO 1 AS LEIS DE NEWTON PROFESSOR ANDERSON VIEIRA Talvez o conceito físico mais intuitivo que carregamos conosco, seja a noção do que é uma força. Muito embora, formalmente, seja algo bastante complicado
PARTE 3. 3.1 Funções Reais de Várias Variáveis Reais
 PARTE 3 FUNÇÕES REAIS DE VÁRIAS VARIÁVEIS REAIS 3. Funções Reais de Várias Variáveis Reais Vamos agora tratar do segundo caso particular de funções vetoriais de várias variáveis reais, F : Dom(F) R n R
PARTE 3 FUNÇÕES REAIS DE VÁRIAS VARIÁVEIS REAIS 3. Funções Reais de Várias Variáveis Reais Vamos agora tratar do segundo caso particular de funções vetoriais de várias variáveis reais, F : Dom(F) R n R
x0 = 1 x n = 3x n 1 x k x k 1 Quantas são as sequências com n letras, cada uma igual a a, b ou c, de modo que não há duas letras a seguidas?
 Recorrências Muitas vezes não é possível resolver problemas de contagem diretamente combinando os princípios aditivo e multiplicativo. Para resolver esses problemas recorremos a outros recursos: as recursões
Recorrências Muitas vezes não é possível resolver problemas de contagem diretamente combinando os princípios aditivo e multiplicativo. Para resolver esses problemas recorremos a outros recursos: as recursões
Funções algébricas do 1º grau. Maurício Bezerra Bandeira Junior
 Maurício Bezerra Bandeira Junior Definição Chama-se função polinomial do 1º grau, ou função afim, a qualquer função f de IR em IR dada por uma lei da forma f(x) = ax + b, onde a e b são números reais dados
Maurício Bezerra Bandeira Junior Definição Chama-se função polinomial do 1º grau, ou função afim, a qualquer função f de IR em IR dada por uma lei da forma f(x) = ax + b, onde a e b são números reais dados
1.5 O oscilador harmónico unidimensional
 1.5 O oscilador harmónico unidimensional A energia potencial do oscilador harmónico é da forma U = 2 2, (1.29) onde é a constante de elasticidade e a deformação da mola. Substituindo (1.29) em (1.24) obtemos
1.5 O oscilador harmónico unidimensional A energia potencial do oscilador harmónico é da forma U = 2 2, (1.29) onde é a constante de elasticidade e a deformação da mola. Substituindo (1.29) em (1.24) obtemos
94 (8,97%) 69 (6,58%) 104 (9,92%) 101 (9,64%) 22 (2,10%) 36 (3,44%) 115 (10,97%) 77 (7,35%) 39 (3,72%) 78 (7,44%) 103 (9,83%)
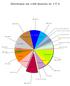 Distribuição das 1.048 Questões do I T A 94 (8,97%) 104 (9,92%) 69 (6,58%) Equações Irracionais 09 (0,86%) Equações Exponenciais 23 (2, 101 (9,64%) Geo. Espacial Geo. Analítica Funções Conjuntos 31 (2,96%)
Distribuição das 1.048 Questões do I T A 94 (8,97%) 104 (9,92%) 69 (6,58%) Equações Irracionais 09 (0,86%) Equações Exponenciais 23 (2, 101 (9,64%) Geo. Espacial Geo. Analítica Funções Conjuntos 31 (2,96%)
Séries de Potências de x
 Séries de Potências de x As séries de potências de x são uma generalização da noção de polinómio. Definição: Chama-se série de potências de x com coeficientes a 0, a 1,, a n,, a qualquer série da forma
Séries de Potências de x As séries de potências de x são uma generalização da noção de polinómio. Definição: Chama-se série de potências de x com coeficientes a 0, a 1,, a n,, a qualquer série da forma
Já vimos que a energia gravitacional entre duas partículas de massas m 1 e m 2, com vetores posição em r 1 e r 2, respectivamente, é dada por
 Força conservativa Já vimos que a energia gravitacional entre duas partículas de massas m 1 e m 2, com vetores posição em r 1 e r 2, respectivamente, é dada por U 12 = Gm 1m 2 r 2 r 1. Vimos também que
Força conservativa Já vimos que a energia gravitacional entre duas partículas de massas m 1 e m 2, com vetores posição em r 1 e r 2, respectivamente, é dada por U 12 = Gm 1m 2 r 2 r 1. Vimos também que
Por que o quadrado de terminados em 5 e ta o fa cil? Ex.: 15²=225, 75²=5625,...
 Por que o quadrado de terminados em 5 e ta o fa cil? Ex.: 15²=225, 75²=5625,... 0) O que veremos na aula de hoje? Um fato interessante Produtos notáveis Equação do 2º grau Como fazer a questão 5 da 3ª
Por que o quadrado de terminados em 5 e ta o fa cil? Ex.: 15²=225, 75²=5625,... 0) O que veremos na aula de hoje? Um fato interessante Produtos notáveis Equação do 2º grau Como fazer a questão 5 da 3ª
Matemática Computacional Ficha 5 (Capítulo 5) 1. Revisão matéria/formulário
 Matemática Computacional Ficha 5 (Capítulo 5) Integração numérica 1. Revisão matéria/formulário A técnica de aproximar o integral de f pelo integral do seu polinómio interpolador passando num conjunto
Matemática Computacional Ficha 5 (Capítulo 5) Integração numérica 1. Revisão matéria/formulário A técnica de aproximar o integral de f pelo integral do seu polinómio interpolador passando num conjunto
Lógica Matemática e Computacional 5 FUNÇÃO
 5 FUNÇÃO 5.1 Introdução O conceito de função fundamenta o tratamento científico de problemas porque descreve e formaliza a relação estabelecida entre as grandezas que o integram. O rigor da linguagem e
5 FUNÇÃO 5.1 Introdução O conceito de função fundamenta o tratamento científico de problemas porque descreve e formaliza a relação estabelecida entre as grandezas que o integram. O rigor da linguagem e
Métodos Numéricos e Estatísticos Parte I-Métodos Numéricos
 Métodos Numéricos e Estatísticos Parte I-Métodos Numéricos Lic. Eng. Biomédica e Bioengenharia-2009/2010 Para determinarmos um valor aproximado das raízes de uma equação não linear, convém notar inicialmente
Métodos Numéricos e Estatísticos Parte I-Métodos Numéricos Lic. Eng. Biomédica e Bioengenharia-2009/2010 Para determinarmos um valor aproximado das raízes de uma equação não linear, convém notar inicialmente
5- CÁLCULO APROXIMADO DE INTEGRAIS 5.1- INTEGRAÇÃO NUMÉRICA
 5- CÁLCULO APROXIMADO DE INTEGRAIS 5.- INTEGRAÇÃO NUMÉRICA Itegrar umericamete uma fução y f() um dado itervalo [a, b] é itegrar um poliômio P () que aproime f() o dado itervalo. Em particular, se y f()
5- CÁLCULO APROXIMADO DE INTEGRAIS 5.- INTEGRAÇÃO NUMÉRICA Itegrar umericamete uma fução y f() um dado itervalo [a, b] é itegrar um poliômio P () que aproime f() o dado itervalo. Em particular, se y f()
Exercícios Teóricos Resolvidos
 Universidade Federal de Minas Gerais Instituto de Ciências Exatas Departamento de Matemática Exercícios Teóricos Resolvidos O propósito deste texto é tentar mostrar aos alunos várias maneiras de raciocinar
Universidade Federal de Minas Gerais Instituto de Ciências Exatas Departamento de Matemática Exercícios Teóricos Resolvidos O propósito deste texto é tentar mostrar aos alunos várias maneiras de raciocinar
Capítulo 5: Aplicações da Derivada
 Instituto de Ciências Exatas - Departamento de Matemática Cálculo I Profª Maria Julieta Ventura Carvalho de Araujo Capítulo 5: Aplicações da Derivada 5- Acréscimos e Diferenciais - Acréscimos Seja y f
Instituto de Ciências Exatas - Departamento de Matemática Cálculo I Profª Maria Julieta Ventura Carvalho de Araujo Capítulo 5: Aplicações da Derivada 5- Acréscimos e Diferenciais - Acréscimos Seja y f
INTRODUÇÃO AO ESTUDO DE EQUAÇÕES DIFERENCIAIS
 INTRODUÇÃO AO ESTUDO DE EQUAÇÕES DIFERENCIAIS Terminologia e Definições Básicas No curso de cálculo você aprendeu que, dada uma função y f ( ), a derivada f '( ) d é também, ela mesma, uma função de e
INTRODUÇÃO AO ESTUDO DE EQUAÇÕES DIFERENCIAIS Terminologia e Definições Básicas No curso de cálculo você aprendeu que, dada uma função y f ( ), a derivada f '( ) d é também, ela mesma, uma função de e
ANÁLISE NUMÉRICA DEC - 1996/97
 ANÁLISE NUMÉRICA DEC - 996/97 Teoria de Erros A Teoria de Erros fornece técnicas para quantificar erros nos dados e nos resultados de cálculos com números aproximados. Nos cálculos aproximados deve-se
ANÁLISE NUMÉRICA DEC - 996/97 Teoria de Erros A Teoria de Erros fornece técnicas para quantificar erros nos dados e nos resultados de cálculos com números aproximados. Nos cálculos aproximados deve-se
Função. Definição formal: Considere dois conjuntos: o conjunto X com elementos x e o conjunto Y com elementos y. Isto é:
 Função Toda vez que temos dois conjuntos e algum tipo de associação entre eles, que faça corresponder a todo elemento do primeiro conjunto um único elemento do segundo, ocorre uma função. Definição formal:
Função Toda vez que temos dois conjuntos e algum tipo de associação entre eles, que faça corresponder a todo elemento do primeiro conjunto um único elemento do segundo, ocorre uma função. Definição formal:
C5. Formação e evolução estelar
 AST434: C5-1/68 AST434: Planetas e Estrelas C5. Formação e evolução estelar Mário João P. F. G. Monteiro Mestrado em Desenvolvimento Curricular pela Astronomia Mestrado em Física e Química em Contexto
AST434: C5-1/68 AST434: Planetas e Estrelas C5. Formação e evolução estelar Mário João P. F. G. Monteiro Mestrado em Desenvolvimento Curricular pela Astronomia Mestrado em Física e Química em Contexto
FEUSP- SEMINÁRIOS DE ENSINO DE MATEMÁTICA-1º semestre/2008 CÁLCULO DIFERENCIAL E INTEGRAL NA ESCOLA BÁSICA: POSSÍVEL E NECESSÁRIO
 1 FEUSP- SEMINÁRIOS DE ENSINO DE MATEMÁTICA-1º semestre/008 CÁLCULO DIFERENCIAL E INTEGRAL NA ESCOLA BÁSICA: POSSÍVEL E NECESSÁRIO Nílson José Machado njmachad@usp.br Sempre que pensamos em grandezas que
1 FEUSP- SEMINÁRIOS DE ENSINO DE MATEMÁTICA-1º semestre/008 CÁLCULO DIFERENCIAL E INTEGRAL NA ESCOLA BÁSICA: POSSÍVEL E NECESSÁRIO Nílson José Machado njmachad@usp.br Sempre que pensamos em grandezas que
Informática no Ensino de Matemática Prof. José Carlos de Souza Junior
 Informática no Ensino de Matemática Prof. José Carlos de Souza Junior http://www.unifal-mg.edu.br/matematica/?q=disc jc Aula 02 ATIVIDADE 01 Para poupar esforço de digitação, você pode usar o tradicional
Informática no Ensino de Matemática Prof. José Carlos de Souza Junior http://www.unifal-mg.edu.br/matematica/?q=disc jc Aula 02 ATIVIDADE 01 Para poupar esforço de digitação, você pode usar o tradicional
Ivan Guilhon Mitoso Rocha. As grandezas fundamentais que serão adotadas por nós daqui em frente:
 Rumo ao ITA Física Análise Dimensional Ivan Guilhon Mitoso Rocha A análise dimensional é um assunto básico que estuda as grandezas físicas em geral, com respeito a suas unidades de medida. Como as grandezas
Rumo ao ITA Física Análise Dimensional Ivan Guilhon Mitoso Rocha A análise dimensional é um assunto básico que estuda as grandezas físicas em geral, com respeito a suas unidades de medida. Como as grandezas
As fases na resolução de um problema real podem, de modo geral, ser colocadas na seguinte ordem:
 1 As notas de aula que se seguem são uma compilação dos textos relacionados na bibliografia e não têm a intenção de substituir o livro-texto, nem qualquer outra bibliografia. Introdução O Cálculo Numérico
1 As notas de aula que se seguem são uma compilação dos textos relacionados na bibliografia e não têm a intenção de substituir o livro-texto, nem qualquer outra bibliografia. Introdução O Cálculo Numérico
MATERIAL MATEMÁTICA I
 MATERIAL DE MATEMÁTICA I CAPÍTULO I REVISÃO Curso: Administração 1 1. Revisão 1.1 Potência de Epoente Inteiro Seja a um número real e m e n números inteiros positivos. Podemos observar as seguintes propriedades
MATERIAL DE MATEMÁTICA I CAPÍTULO I REVISÃO Curso: Administração 1 1. Revisão 1.1 Potência de Epoente Inteiro Seja a um número real e m e n números inteiros positivos. Podemos observar as seguintes propriedades
INTRODUÇÃO AOS MÉTODOS FACTORIAIS
 Capítulo II INTRODUÇÃO AOS MÉTODOS FACTORIAIS A Análise Factorial de Correspondências é uma técnica simples do ponto de vista matemático e computacional. Porém, devido ao elevado suporte geométrico desta
Capítulo II INTRODUÇÃO AOS MÉTODOS FACTORIAIS A Análise Factorial de Correspondências é uma técnica simples do ponto de vista matemático e computacional. Porém, devido ao elevado suporte geométrico desta
2 Independência e dependência das taxas de juro
 1 Incerteza e juro aleatório Considere-se o intervalo [0, n], o tempo medido em anos, e a partição [0, 1], (1, 2],..., (n 1, 1] e suponha-se que no início do ano t são aplicadas C t unidades de capital,
1 Incerteza e juro aleatório Considere-se o intervalo [0, n], o tempo medido em anos, e a partição [0, 1], (1, 2],..., (n 1, 1] e suponha-se que no início do ano t são aplicadas C t unidades de capital,
CI202 - Métodos Numéricos
 CI202 - Métodos Numéricos Lista de Exercícios 2 Zeros de Funções Obs.: as funções sen(x) e cos(x) devem ser calculadas em radianos. 1. Em geral, os métodos numéricos para encontrar zeros de funções possuem
CI202 - Métodos Numéricos Lista de Exercícios 2 Zeros de Funções Obs.: as funções sen(x) e cos(x) devem ser calculadas em radianos. 1. Em geral, os métodos numéricos para encontrar zeros de funções possuem
A seguir, uma demonstração do livro. Para adquirir a versão completa em papel, acesse: www.pagina10.com.br
 A seguir, uma demonstração do livro. Para adquirir a versão completa em papel, acesse: www.pagina0.com.br Funções Reais CÁLCULO VOLUME ZERO - Neste capítulo, estudaremos as protagonistas do longa metragem
A seguir, uma demonstração do livro. Para adquirir a versão completa em papel, acesse: www.pagina0.com.br Funções Reais CÁLCULO VOLUME ZERO - Neste capítulo, estudaremos as protagonistas do longa metragem
E A D - S I S T E M A S L I N E A R E S INTRODUÇÃO
 E A D - S I S T E M A S L I N E A R E S INTRODUÇÃO Dizemos que uma equação é linear, ou de primeiro grau, em certa incógnita, se o maior expoente desta variável for igual a um. Ela será quadrática, ou
E A D - S I S T E M A S L I N E A R E S INTRODUÇÃO Dizemos que uma equação é linear, ou de primeiro grau, em certa incógnita, se o maior expoente desta variável for igual a um. Ela será quadrática, ou
Equações Diferenciais Ordinárias
 Capítulo 8 Equações Diferenciais Ordinárias Vários modelos utilizados nas ciências naturais e exatas envolvem equações diferenciais. Essas equações descrevem a relação entre uma função, o seu argumento
Capítulo 8 Equações Diferenciais Ordinárias Vários modelos utilizados nas ciências naturais e exatas envolvem equações diferenciais. Essas equações descrevem a relação entre uma função, o seu argumento
Organização e Arquitetura de Computadores I
 Organização e Arquitetura de Computadores I Aritmética Computacional Slide 1 Sumário Unidade Lógica e Aritmética Representação de Números Inteiros Aritmética de Números Inteiros Representação de Números
Organização e Arquitetura de Computadores I Aritmética Computacional Slide 1 Sumário Unidade Lógica e Aritmética Representação de Números Inteiros Aritmética de Números Inteiros Representação de Números
CDI-II. Trabalho. Teorema Fundamental do Cálculo
 Instituto Superior Técnico Departamento de Matemática Secção de Álgebra e Análise Prof. Gabriel Pires CDI-II Trabalho. Teorema Fundamental do Cálculo 1 Trabalho. Potencial Escalar Uma das noções mais importantes
Instituto Superior Técnico Departamento de Matemática Secção de Álgebra e Análise Prof. Gabriel Pires CDI-II Trabalho. Teorema Fundamental do Cálculo 1 Trabalho. Potencial Escalar Uma das noções mais importantes
ARQUITETURA DE COMPUTADORES. Sistemas de Numeração. 1 Arquitetura de Computadores
 ARQUITETURA DE COMPUTADORES Sistemas de Numeração 1 Sistemas de Numeração e Conversão de Base Sistema Decimal É o nosso sistema natural. Dígitos 0,1,2,3,4,5,6,7,8 e 9. Números superiores a 9; convencionamos
ARQUITETURA DE COMPUTADORES Sistemas de Numeração 1 Sistemas de Numeração e Conversão de Base Sistema Decimal É o nosso sistema natural. Dígitos 0,1,2,3,4,5,6,7,8 e 9. Números superiores a 9; convencionamos
3.400 17. ( ) 100 3400 6000, L x x. L x x x. (17) 34 60 Lx ( ) 17 34 17 60 L(17) 289 578 60 L(17) 289 638 L(17) 349 40 40 70.40 40 1.
 REDE ISAAC NEWTON ENSINO MÉDIO 3º ANO PROFESSOR(A):LUCIANO IEIRA DATA: / / TURMA: ALUNO(A): Nº: UNIDADE: ( ) Riacho Fundo ( ) Taguatinga Sul EXERCÍCIOS DE REISÃO - AALIAÇÃO ESPECÍFICA 3º TRIMESTRE 01 MATEMÁTICA
REDE ISAAC NEWTON ENSINO MÉDIO 3º ANO PROFESSOR(A):LUCIANO IEIRA DATA: / / TURMA: ALUNO(A): Nº: UNIDADE: ( ) Riacho Fundo ( ) Taguatinga Sul EXERCÍCIOS DE REISÃO - AALIAÇÃO ESPECÍFICA 3º TRIMESTRE 01 MATEMÁTICA
Aula 19 06/2014. Integração Numérica
 CÁLCULO NUMÉRICO Aula 19 06/2014 Integração Numérica Objetivo: Calcular integrais utilizando métodos numéricos Cálculo Numérico 3/41 Integração Numérica Cálculo Numérico 4/41 Integração Numérica Em determinadas
CÁLCULO NUMÉRICO Aula 19 06/2014 Integração Numérica Objetivo: Calcular integrais utilizando métodos numéricos Cálculo Numérico 3/41 Integração Numérica Cálculo Numérico 4/41 Integração Numérica Em determinadas
4.2 Teorema do Valor Médio. Material online: h-p://www.im.ufal.br/professor/thales/calc1-2010_2.html
 4.2 Teorema do Valor Médio Material online: h-p://www.im.ufal.br/professor/thales/calc1-2010_2.html Teorema de Rolle: Seja f uma função que satisfaça as seguintes hipóteses: a) f é contínua no intervalo
4.2 Teorema do Valor Médio Material online: h-p://www.im.ufal.br/professor/thales/calc1-2010_2.html Teorema de Rolle: Seja f uma função que satisfaça as seguintes hipóteses: a) f é contínua no intervalo
INSTITUTO POLITÉCNICO DE VISEU ESCOLA SUPERIOR DE TECNOLOGIA DE VISEU DEPARTAMENTO DE MATEMÁTICA
 INSTITUTO POLITÉCNICO DE VISEU ESCOLA SUPERIOR DE TECNOLOGIA DE VISEU DEPARTAMENTO DE MATEMÁTICA Apontamentos: Curso de Conhecimentos Básicos de Matemática Cursos do Departamento de Gestão Maria Cristina
INSTITUTO POLITÉCNICO DE VISEU ESCOLA SUPERIOR DE TECNOLOGIA DE VISEU DEPARTAMENTO DE MATEMÁTICA Apontamentos: Curso de Conhecimentos Básicos de Matemática Cursos do Departamento de Gestão Maria Cristina
Definição. A expressão M(x,y) dx + N(x,y)dy é chamada de diferencial exata se existe uma função f(x,y) tal que f x (x,y)=m(x,y) e f y (x,y)=n(x,y).
 PUCRS FACULDADE DE ATEÁTICA EQUAÇÕES DIFERENCIAIS PROF. LUIZ EDUARDO OURIQUE EQUAÇÔES EXATAS E FATOR INTEGRANTE Definição. A diferencial de uma função de duas variáveis f(x,) é definida por df = f x (x,)dx
PUCRS FACULDADE DE ATEÁTICA EQUAÇÕES DIFERENCIAIS PROF. LUIZ EDUARDO OURIQUE EQUAÇÔES EXATAS E FATOR INTEGRANTE Definição. A diferencial de uma função de duas variáveis f(x,) é definida por df = f x (x,)dx
Resolução de sistemas lineares
 Resolução de sistemas lineares J M Martínez A Friedlander 1 Alguns exemplos Comecemos mostrando alguns exemplos de sistemas lineares: 3x + 2y = 5 x 2y = 1 (1) 045x 1 2x 2 + 6x 3 x 4 = 10 x 2 x 5 = 0 (2)
Resolução de sistemas lineares J M Martínez A Friedlander 1 Alguns exemplos Comecemos mostrando alguns exemplos de sistemas lineares: 3x + 2y = 5 x 2y = 1 (1) 045x 1 2x 2 + 6x 3 x 4 = 10 x 2 x 5 = 0 (2)
Em um sistema de numeração de base b qualquer, um número positivo é representado pelo polinômio:
 ELETRÔNICA DIGITAl I 1 SISTEMAS DE NUMERAÇÃO INTRODUÇÃO A base dos sistemas digitais são os circuitos de chaveamento (switching) nos quais o componente principal é o transistor que, sob o ponto de vista
ELETRÔNICA DIGITAl I 1 SISTEMAS DE NUMERAÇÃO INTRODUÇÃO A base dos sistemas digitais são os circuitos de chaveamento (switching) nos quais o componente principal é o transistor que, sob o ponto de vista
3. Características amostrais. Medidas de localização e dispersão
 Estatística Descritiva com Excel Complementos. 77 3. Características amostrais. Medidas de localização e dispersão 3.1- Introdução No módulo de Estatística foram apresentadas as medidas ou estatísticas
Estatística Descritiva com Excel Complementos. 77 3. Características amostrais. Medidas de localização e dispersão 3.1- Introdução No módulo de Estatística foram apresentadas as medidas ou estatísticas
A EVOLUÇÃO DOS PRODUTOS NA INDÚSTRIA TRANSFORMADORA
 A EVOLUÇÃO DOS PRODUTOS NA INDÚSTRIA TRANSFORMADORA O ciclo de fabrico característico abrange as seguintes fases: Compra de matérias e serviços Transformação das matérias-primas em produtos acabados Venda
A EVOLUÇÃO DOS PRODUTOS NA INDÚSTRIA TRANSFORMADORA O ciclo de fabrico característico abrange as seguintes fases: Compra de matérias e serviços Transformação das matérias-primas em produtos acabados Venda
Soluções Nível 1 5 a e 6 a séries (6º e 7º anos) do Ensino Fundamental
 a e 6 a séries (6º e 7º anos) do Ensino Fundamental 1. (alternativa C) Os números 0,01 e 0,119 são menores que 0,12. Por outro lado, 0,1 e 0,7 são maiores que 0,. Finalmente, 0,29 é maior que 0,12 e menor
a e 6 a séries (6º e 7º anos) do Ensino Fundamental 1. (alternativa C) Os números 0,01 e 0,119 são menores que 0,12. Por outro lado, 0,1 e 0,7 são maiores que 0,. Finalmente, 0,29 é maior que 0,12 e menor
Fundamentos da Metrologia Científica e Industrial Ambiente Virtual: Balança Digital
 Fundamentos da Metrologia Científica e Industrial Ambiente Virtual: Balança Digital 1. Apresentação Quatro elementos estão disponíveis no ambiente virtual: Balança digital a ser calibrada Coleção de massas
Fundamentos da Metrologia Científica e Industrial Ambiente Virtual: Balança Digital 1. Apresentação Quatro elementos estão disponíveis no ambiente virtual: Balança digital a ser calibrada Coleção de massas
Aula 5 - Matemática (Gestão e Marketing)
 ISCTE, Escola de Gestão Aula 5 - Matemática (Gestão e Marketing) Diana Aldea Mendes 29 de Outubro de 2008 Espaços Vectoriais Definição (vector): Chama-se vector edesigna-sepor v um objecto matemático caracterizado
ISCTE, Escola de Gestão Aula 5 - Matemática (Gestão e Marketing) Diana Aldea Mendes 29 de Outubro de 2008 Espaços Vectoriais Definição (vector): Chama-se vector edesigna-sepor v um objecto matemático caracterizado
Representação de Dados
 Representação de Dados Introdução Todos sabemos que existem diferentes tipos de números: fraccionários, inteiros positivos e negativos, etc. Torna-se necessária a representação destes dados em sistema
Representação de Dados Introdução Todos sabemos que existem diferentes tipos de números: fraccionários, inteiros positivos e negativos, etc. Torna-se necessária a representação destes dados em sistema
Resolução dos Exercícios sobre Derivadas
 Resolução dos Eercícios sobre Derivadas Eercício Utilizando a idéia do eemplo anterior, encontre a reta tangente à curva nos pontos onde e Vamos determinar a reta tangente à curva nos pontos de abscissas
Resolução dos Eercícios sobre Derivadas Eercício Utilizando a idéia do eemplo anterior, encontre a reta tangente à curva nos pontos onde e Vamos determinar a reta tangente à curva nos pontos de abscissas
MANUAL DO UTILIZADOR
 MANUAL DO UTILIZADOR Versão 1.6 PÁGINA DE PESQUISA A página principal do PacWeb permite a realização de um número muito variado de pesquisas, simples, ou pelo contrário extremamente complexas, dependendo
MANUAL DO UTILIZADOR Versão 1.6 PÁGINA DE PESQUISA A página principal do PacWeb permite a realização de um número muito variado de pesquisas, simples, ou pelo contrário extremamente complexas, dependendo
Conceitos Fundamentais
 Capítulo 1 Conceitos Fundamentais Objetivos: No final do Capítulo o aluno deve saber: 1. distinguir o uso de vetores na Física e na Matemática; 2. resolver sistema lineares pelo método de Gauss-Jordan;
Capítulo 1 Conceitos Fundamentais Objetivos: No final do Capítulo o aluno deve saber: 1. distinguir o uso de vetores na Física e na Matemática; 2. resolver sistema lineares pelo método de Gauss-Jordan;
Métodos Matemáticos para Gestão da Informação
 Métodos Matemáticos para Gestão da Informação Aula 05 Taxas de variação e função lineares III Dalton Martins dmartins@gmail.com Bacharelado em Gestão da Informação Faculdade de Informação e Comunicação
Métodos Matemáticos para Gestão da Informação Aula 05 Taxas de variação e função lineares III Dalton Martins dmartins@gmail.com Bacharelado em Gestão da Informação Faculdade de Informação e Comunicação
Conceitos e fórmulas
 1 Conceitos e fórmulas 1).- Triângulo: definição e elementos principais Definição - Denominamos triângulo (ou trilátero) a toda figura do plano euclidiano formada por três segmentos AB, BC e CA, tais que
1 Conceitos e fórmulas 1).- Triângulo: definição e elementos principais Definição - Denominamos triângulo (ou trilátero) a toda figura do plano euclidiano formada por três segmentos AB, BC e CA, tais que
APLICAÇÕES DA DERIVADA
 Notas de Aula: Aplicações das Derivadas APLICAÇÕES DA DERIVADA Vimos, na seção anterior, que a derivada de uma função pode ser interpretada como o coeficiente angular da reta tangente ao seu gráfico. Nesta,
Notas de Aula: Aplicações das Derivadas APLICAÇÕES DA DERIVADA Vimos, na seção anterior, que a derivada de uma função pode ser interpretada como o coeficiente angular da reta tangente ao seu gráfico. Nesta,
Exercícios de MATEMÁTICA COMPUTACIONAL Capítulo V
 Exercícios de MATEMÁTICA COMPUTACIONAL Capítulo V Integração Numérica 1. Considere o integral: 1 0 e x2 dx a) Determine o seu valor aproximado, considerando 4 subintervalos e utilizando: i. A regra dos
Exercícios de MATEMÁTICA COMPUTACIONAL Capítulo V Integração Numérica 1. Considere o integral: 1 0 e x2 dx a) Determine o seu valor aproximado, considerando 4 subintervalos e utilizando: i. A regra dos
1 A Integral por Partes
 Métodos de Integração Notas de aula relativas aos dias 14 e 16/01/2004 Já conhecemos as regras de derivação e o Teorema Fundamental do Cálculo. Este diz essencialmente que se f for uma função bem comportada,
Métodos de Integração Notas de aula relativas aos dias 14 e 16/01/2004 Já conhecemos as regras de derivação e o Teorema Fundamental do Cálculo. Este diz essencialmente que se f for uma função bem comportada,
Truques e Dicas. = 7 30 Para multiplicar fracções basta multiplicar os numeradores e os denominadores: 2 30 = 12 5
 Truques e Dicas O que se segue serve para esclarecer alguma questão que possa surgir ao resolver um exercício de matemática. Espero que lhe seja útil! Cap. I Fracções. Soma e Produto de Fracções Para somar
Truques e Dicas O que se segue serve para esclarecer alguma questão que possa surgir ao resolver um exercício de matemática. Espero que lhe seja útil! Cap. I Fracções. Soma e Produto de Fracções Para somar
Matemática - UEL - 2010 - Compilada em 18 de Março de 2010. Prof. Ulysses Sodré Matemática Essencial: http://www.mat.uel.
 Matemática Essencial Equações do Segundo grau Conteúdo Matemática - UEL - 2010 - Compilada em 18 de Março de 2010. Prof. Ulysses Sodré Matemática Essencial: http://www.mat.uel.br/matessencial/ 1 Introdução
Matemática Essencial Equações do Segundo grau Conteúdo Matemática - UEL - 2010 - Compilada em 18 de Março de 2010. Prof. Ulysses Sodré Matemática Essencial: http://www.mat.uel.br/matessencial/ 1 Introdução
)LJXUD8PGRVSDUHV'SDUDFRQYROXomRTXHWHPRPHVPRHIHLWRGR NHUQHOGD)LJXUD
 )LOWURJDXVVLDQR O filtro Gaussiano pode ser usado como um filtro SDVVDEDL[D. Usando a função Gaussiana para obter valores de uma máscara a ser definida digitalmente. O Filtro de Gaussiano em 1-D tem a
)LOWURJDXVVLDQR O filtro Gaussiano pode ser usado como um filtro SDVVDEDL[D. Usando a função Gaussiana para obter valores de uma máscara a ser definida digitalmente. O Filtro de Gaussiano em 1-D tem a
Conjuntos numéricos. Notasdeaula. Fonte: Leithold 1 e Cálculo A - Flemming. Dr. Régis Quadros
 Conjuntos numéricos Notasdeaula Fonte: Leithold 1 e Cálculo A - Flemming Dr. Régis Quadros Conjuntos numéricos Os primeiros conjuntos numéricos conhecidos pela humanidade são os chamados inteiros positivos
Conjuntos numéricos Notasdeaula Fonte: Leithold 1 e Cálculo A - Flemming Dr. Régis Quadros Conjuntos numéricos Os primeiros conjuntos numéricos conhecidos pela humanidade são os chamados inteiros positivos
