Produto Misto, Determinante e Volume
|
|
|
- Jessica Aurora Sales Regueira
- 7 Há anos
- Visualizações:
Transcrição
1 15 Produto Misto, Determinante e Volume Sumário 15.1 Produto Misto e Determinante Regra de Cramer Operações com matrizes Exercícios
2 Unidade 15 Produto Misto e Determinante 15.1 Produto Misto e Determinante O produto misto dos vetores u, v e w do espaço é o número real [ u, v, w ] = u v, w. O produto misto de u, v e w nada mais é, pela propriedade (8) do produto vetorial, que o determinante da matriz do tipo 3 3 que tem por linhas as coordenadas dos vetores u, v e w na ordem em que são listados. Ou seja, [ u, v, w ] = det( u, v, w ). Interpretação geométrica do produto misto Sejam A, B, C e D pontos não coplanares e P o paralelepípedo que tem os segmentos AB, AC e AD como arestas adjacentes. Considerando o paralelogramo T de lados adjacentes AB e AC como base de P, Vol (P) = Área (T ) h, onde h é a altura de P relativa à base u v h O θ C w P B v T u Figura 15.1: Interpretação geométrica do produto T (ver Figura 15.1). misto. Se u = AB, v = AC e w = AD, obtemos que Área (T ) = u v e h = w cos ( w, u v ). Portanto, Vol (P) = u v w cos ( w, u v ). Ou seja, o volume de P é o módulo do produto misto dos vetores u, v w : Vol (P) = [ u, v, w ], ou, em termos dos vértices A, B, C e D, Vol (P) = [ AB, AC, AD ]. u Por outro lado, se os pontos A, B, C e D são coplanares, isto é, se os vetores = AB, v = AC e w = AD são L.D., o paralelepípedo ca reduzido a um paralelogramo, a um segmento ou a um ponto, tendo, portanto, volume zero. Isto concorda com a propriedade (9) do produto vetorial: se u, v são L.D., então [ u, v, w ] = 0. A e w e 2
3 Produto Misto, Determinante e Volume Unidade 15 (Propriedades do produto misto) Sejam u, u 0, v, v 0, w e w 0 vetores do Proposição 1 espaço e seja λ R. Então: (1) [λ u, v, w ] = [ u, λ v, w ] = [ u, v, λ w ] = λ[ u, v, w ] ; (2) [ u + u 0, v, w ] = [ u, v, w ] + [ u 0, v, w ] ; [ u, v + v 0, w ] = [ u, v, w ] + [ u, v 0, w ] ; [ u, v, w + w 0 ] = [ u, v, w ] + [ u, v, w 0 ] ; (3) [ u, v, w ] = 0 se, e somente, se, os vetores u, v e w são L.D.. Ou seja, [ u, v, w ] 0 se, e somente se, u, v e w são L.I.; (4) O sinal do produto misto muda quando permutamos dois de seus fatores: [ u, v, w ] = [ v, u, w ], [ u, v, w ] = [ w, v, u ], [ u, v, w ] = [ u, w, v ]. As propriedades (1), (2), (3) e a primeira identidade da propriedade (4) seguem diretamente das propriedades do produto vetorial e do produto interno. Demonstração Precisamos provar as outras identidades da propriedade (4). Sejam u = (x 1, y 1, z 1 ), v = (x 2, y 2, z 2 ) e w = (x 3, y 3, z 3 ) os vetores dados num sistema de eixos ortogonais OXY Z positivo. Temos: u v, w = x 3 (y 1 z 2 y 2 z 1 ) y 3 (x 1 z 2 x 2 z 1 ) + z 3 (x 1 y 2 x 2 y 1 ) = x 1 (y 2 z 3 y 3 z 2 ) y 1 (x 2 z 3 x 3 z 2 ) + z 1 (x 2 y 3 x 3 y 2 ) = v w, u. (15.1) Como v w = ( w v ), segue, de 15.1, que u v, w = v w, u = w v, u. Logo, [ u, v, w ] = [ w, v, u ]. (15.2) que é a segunda identidade da propriedade (4). Permutando os vetores v e u, obtemos, pelo provado acima, que [ v, w, u ] = [ u, w, v ]. (15.3) 3
4 Unidade 15 Produto Misto e Determinante Assim, por 15.2 e 15.3, [ u, v, w ] = [ w, v, u ] = [ v, w, u ] = [ u, w, v ], que é a terceira identidade da propriedade (4). Como, consequência, seque que se zermos duas permutações seguidas dos vetores u, v De fato, e w, o produto misto não se altera: [ u, v, w ] = [ w, u, v ] = [ v, w, u ]. [ u, v, w ] = [ w, v, u ] = ( [ v, w, u ]) = [ v, w, u ], [ u, v, w ] = [ v, u, w ] = ( [ w, u, v ]) = [ w, u, v ]. Exemplo 1 Verique se os pontos A = (1, 2, 1), B = (4, 1, 2), C = (3, 3, 3) e D = (0, 4, 2) são coplanares. Solução. Sejam os vetores AB = (3, 1, 1), AC = (2, 1, 2) e AD = ( 1, 2, 1). Pela propriedade (3) do produto misto e pela Observação 9 do Capítulo 14, os pontos A, B, C e D são coplanares se, e somente se, [ AB, AC, AD ] = 0. Calculando, AB AC = obtemos que ( ) , , = ( 3, 4, 5), [ AB, AC, AD ] = AB AC, AD = ( 3, 4, 5), ( 1, 2, 1) = 0. Portanto, os pontos A, B, C e D são coplanares. Observe que AD = AB + AC. Exemplo 2 Mostre que os vetores u = (1, 0, 2), v = (2, 1, 0) e w = (3, 1, 1) são L.I., e calcule o volume do paralelepípedo P cujas arestas adjacentes são representantes dos vetores u, v e w. Solução. Pela propriedade (3), u, v e w são L.I. se, e só se, [ u, v, w ] 0. 4
5 Produto Misto, Determinante e Volume Unidade 15 Como [ u, v, w ] = u v, w = = 3( 2) ( 4) + 1 os vetores u, v = = 1 0, e w são L.I. e o volume do paralelepípedo P é Vol (P) = [ u, v, w ] = 1 = 1. Sendo det( u, v, w ) = [ u, v, w ], podemos traduzir as propriedades do produto misto em propriedades do determinante de uma matriz Multiplicar uma linha por um número real λ, equivale a multiplicar o determinante por λ: det(λ u, v, w ) = det( u, λ v, w ) = det( u, v, λ w ) = λ det( u, v, w ). 2. A soma dos determinantes de duas matrizes com duas linhas em comum é o determinante da matriz que tem essas duas linhas comuns e o vetor linha restante igual a soma dos vetores linha correspondentes das duas matrizes: det( u, v, w ) + det( u 0, v, w ) = det( u + u 0, v, w ), det( u, v, w ) + det( u, v 0, w ) = det( u, v + v 0, w ), det( u, v, w ) + det( u, v, w 0 ) = det( u, v, w + w 0 ). 3. Critério de coplanaridade: det( u, v, w ) = 0 u, v e w são coplanares (L.D.), det( u, v, w ) 0 u, v e w não são coplanares (L.I.). 4. O sinal do determinante muda quando se permuta duas de suas linhas: det( v, u, w ) = det( u, v, w ), det( w, v, u ) = det( u, v, w ), det( u, w, v ) = det( u, v, w ). Como consequência das propriedades (1), (2) e (3), obtemos as seguintes propriedades: 5. Se uma matriz tem duas linhas iguais, seu determinante é igual a zero: 5
6 Unidade 15 Produto Misto e Determinante det( u, u, v ) = det( u, v, u ) = det( u, v, v ) = Se uma linha da matriz é combinação linear das outras duas, o determinante da matriz é zero: det(α v + β w, v, w ) = det( u, α u + β w, w ) = det( u, v, α u + β v ) = O determinante de uma matriz não se altera se trocarmos uma de suas linhas pela soma dela com um múltiplo de outra. Por exemplo, det( u + α v, v, w ) = det( u, v, w ). De fato, pelas propriedades (1), (2) e (5), det( u + α v, v, w ) = det( u, v, w ) + α det( v, v, w ) = det( u, v, w ). 8. Se u = (x 1, y 1, z 1 ), v = (x 2, y 2, z 2 ) e w = (x 3, y 3, z 3 ) são os vetores num sistema de eixos ortogonais OXY Z, então: det( u, v, w ) = det( v, w, u ) = v w, u = y = x 2 z 2 1 y 3 z 3 y 1 x 2 z 2 x 3 z 3 + z 1 x 2 y 2 x 3 y 3 = ( 1) 1+1 y x 2 z 2 1 y 3 z 3 + x ( 1)1+2 y 2 z 2 1 x 3 z 3 + x ( 1)1+3 z 2 y 2 1 x 3 y 3 é o desenvolvimento do determinante da matriz segundo a primeira linha; det( u, v, w ) = det( u, w, v ) = u w, v = y = x 1 z 1 2 y 3 z 3 + y 2 x 1 z 1 x 3 z 3 z 2 x 1 y 1 x 3 y 3 = ( 1) 2+1 y x 1 z 1 2 y 3 z 3 + x ( 1)2+2 y 1 z 1 2 x 3 z 3 + x ( 1)2+3 z 1 y 1 2 x 3 y 3 é o desenvolvimento do determinante da matriz segundo a segunda linha; det( u, v, w ) = u v, w = y = x 1 z 1 3 y 2 z 2 y 3 x 1 z 1 x 2 z 2 + z 3 x 1 y 1 x 2 y 2 = ( 1) 3+1 y x 1 z 1 3 y 2 z 2 + x ( 1)3+2 y 1 z 1 3 x 2 z 2 + x ( 1)3+3 z 1 y 1 3 x 2 y 2 é o desenvolvimento do determinante da matriz segundo a terceira linha. 6
7 Produto Misto, Determinante e Volume Unidade 15 No fator ( 1) i+j, das identidades acima, i indica a i ésima linha e j indica a j ésima coluna, i, j = 1, 2, 3. Sejam A uma matriz 3 3 e r o elemento de A que ocupa a i ésima linha e a j ésima coluna. O menor A ij relativo a esse elemento é o determinante da matriz 2 2 que se obtém omitindo-se a i ésima linha e a j ésima coluna de A. Ou seja, se x 1 y 1 z 1 A = x 2 y 2 z 2, então: x 3 y 3 z 3 A 11 = y 2 z 2 y 3 z 3, A 12 = x 2 z 2 x 3 z 3, A 13 = x 2 y 2 x 3 z 3, A 21 = y 1 z 1 y 3 z 3, A 22 = x 1 z 1 x 3 z 3, A 23 = x 1 y 1 x 3 z 3, A 31 = y 1 z 1 y 2 z 2, A 32 = x 1 z 1 x 2 z 2, A 33 = x 1 y 1 x 2 z 3. Assim, o desenvolvimento do determinante da matriz A segundo a primeira, a segunda e a terceira linha são dadas, respectivamente, por: det A = ( 1) 1+1 x 1 A 11 + ( 1) 1+2 y 1 A 12 + ( 1) 1+3 z 1 A 13, det A = ( 1) 2+1 x 2 A 21 + ( 1) 2+2 y 2 A 22 + ( 1) 2+3 z 2 A 23, det A = ( 1) 3+1 x 3 A 31 + ( 1) 3+2 y 3 A 32 + ( 1) 3+3 z 3 A 33. Exemplo 3 Calcule o determinante da matriz A, desenvolvendo-o segundo a primeira, a segunda e a terceira linha, onde A = Solução. Temos: det A = ( 1) ( 1) ( 1) = 3(1 + 2) 2(0 8) + (0 4) = = 21, 7
8 Unidade 15 Produto Misto e Determinante det A = ( 1) ( 1) ( 1) = (3 4) 2( 3 8) = = 21, det A = ( 1) ( 1)3+2 ( 1) ( 1) = 4(4 1) + (6 0) + (3 0) = = 21. Exemplo 4 Uma matriz A é uma matriz diagonal se todos os elementos de A que não estão na diagonal são iguais a zero. Ou seja, se A é da forma λ A = 0 λ 2 0 ; λ 1, λ 2, λ 3 R. 0 0 λ 3 Desenvolvendo o determinante de A pela primeira linha, obtemos det(a) = ( 1) 1+1 λ λ λ 3 = λ 1λ 2 λ 3. A matriz identidade I do tipo 3 3 é a matriz diagonal com λ 1 = λ 2 = λ 3 = 1. Então, I = e seu determinante é igual a um A matriz transposta da matriz A é a matriz A T cuja i ésima coluna é a i ésima linha da matriz A. Ou seja, se A = x 1 y 1 z 1 x 2 y 2 z 2 = A T = x 1 x 2 x 3 y 1 y 2 y 3. x 3 y 3 z 3 z 1 z 2 z 3 9. O determinante da matriz A é igual ao determinante de sua matriz transposta A T. De fato, pelo desenvolvimento do determinante da matriz A T com respeito à sua primeira linha, 8
9 Produto Misto, Determinante e Volume Unidade 15 det A T = y x 2 y 3 1 z 2 z 3 x 2 y 1 y 3 z 1 z 3 + x 3 y 1 y 2 z 1 z 2 = x 1 (y 2 z 3 y 3 z 2 ) x 2 (y 1 z 3 y 3 z 1 ) + x 3 (y 1 z 2 y 2 z 1 ) = x 1 (y 2 z 3 y 3 z 2 ) y 1 (x 2 z 3 x 3 y 2 ) + z 1 (x 2 y 3 x 3 y 2 ) = y x 2 z 2 1 y 3 z 3 y 1 x 2 z 2 x 3 z 3 + z 1 x 2 y 2 x 3 y 3., obtemos que det A T = det A. Portanto, todas as propriedades do determinante com respeito às suas linhas também valem para suas colunas. Em particular: 10. Os vetores coluna da matriz A são L.I. se, e somente se, det(a) O determinante da matriz A pode ser calculado segundo os elementos da: 1 a coluna: det A = ( 1) 1+1 y x 2 z 2 1 y 3 z 3 + y ( 1)2+1 x 1 z 1 2 y 3 z 3 + y ( 1)3+1 x 1 z 1 3 y 2 z 2 = ( 1) 1+1 x 1 A 11 + ( 1) 2+1 x 2 A 21 + ( 1) 3+1 x 3 A 31, 2 a coluna: det A = ( 1) 1+2 x y 2 z 2 1 x 3 z 3 + x ( 1)2+2 y 1 z 1 2 x 3 z 3 + x ( 1)3+2 y 1 z 1 3 x 2 z 2 = ( 1) 1+2 y 1 A 12 + ( 1) 2+2 y 2 A 22 + ( 1) 3+2 y 3 A 32, 3 a coluna: det A = ( 1) 1+3 x z 2 y 2 1 x 3 y 3 + x ( 1)2+3 z 1 y 1 2 x 3 y 3 + x ( 1)3+3 z 1 y 1 3 x 2 y 2 = ( 1) 1+3 z 1 A 13 + ( 1) 2+3 z 2 A 23 + ( 1) 3+3 z 3 A 33. O cálculo do determinante de uma matriz A pelo desenvolvimento segundo uma linha ou uma coluna é muito útil quando a matriz A tem uma linha ou coluna com um ou dois elementos iguais a zero. Pelo desenvolvimento segundo a terceira linha, que possui um elemento igual a zero, temos Exemplo 5 9
10 Unidade 15 Regra de Cramer det = ( 1) ( 1) = = 32, e pelo desenvolvimento com respeito à primeira coluna, que tem dois elementos iguais a zero, obtemos det = ( 1) = 4(6 14) = Regra de Cramer Frequentemente enfrentamos a necessidade de resolver um sistema de três equações lineares com três variáveis. Um método para atingir tal objetivo é a Regra de Cramer. Consideremos o sistema de três equações lineares a três incógnitas x, y e z: a 1 x + b 1 y + c 1 z = d 1 a 2 x + b 2 y + c 2 z = d 2 a 3 x + b 3 y + c 3 z = d 3. a 1 b 1 c 1 A matriz A = a 2 b 2 c 2 é chamada matriz do sistema. Sabemos que a 3 b 3 c 3 det A 0 as linhas de A são L.I. as colunas de A são L.I.. Consideremos os vetores coluna da matriz A, a = (a1, a 2, a 3 ), b = (b 1, b 2, b 3 ), c = (c 1, c 2, c 3 ), e o vetor d = (d 1, d 2, d 3 ) formado pelos termos independentes do sistema. que Resolver o sistema acima equivale, então, a determinar os x, y, z R tais x a + y b + z c = d, ou seja, consiste em encontrar os coecientes de a, b e c mediante os quais o vetor d se escreve como combinação linear desses três vetores. 10
11 Produto Misto, Determinante e Volume Unidade 15 Aplicando as propriedades do determinante obtidas anteriormente, temos: det( d, b, c ) = det(x a + y b + z c, b, c ) = x det( a, b, c ) + y det( b, b, c ) + z det( c, b, c ) = x det( a, b, c ). Portanto, se det( a, b, c ) 0, x = det( d, b, c ) det( a, b, c ). Analogamente, calculando os determinantes das matrizes ( a, d, c ) e ( a, b, d ), obtemos: y = det( a, d, c ) det( a, b, c ) e z = det( a, b, d ) det( a, b, c ). Estas três fórmulas, que fornecem as incógnitas x, y e z como quocientes de dois determinantes, constituem a regra de Cramer. Observe que det A = det( a, b, c ), pois a matriz cujos vetores linha são a, b e c é a transposta da matriz A. Embora a regra de Cramer nos dê um método para achar a solução de um sistema, ela é muito trabalhosa. sistema de modo bem simples e geométrico. No Capítulo 18 veremos como resolver um Verique que o sistema abaixo possui uma única solução e use a regra de Exemplo 6 Cramer para determiná-la: x + y + 2z = 1 2x + 3y + 3z = 2 4x + 4y + 5z = 3. Solução. Sejam a = (1, 2, 4), b = (1, 3, 4), e c = (2, 3, 5) os vetores coluna da matriz do sistema e d independentes. Calculando, obtemos det( a, b, c ) = 3 0. = (1, 2, 3) o vetor formado pelos termos Portanto, o sistema possui uma solução. Como det( d, b, c ) = 0, det( a, d, c ) = 1, det( a, b, d ) = 1, temos, pela regra de Cramer, que: x = det( d, b, c ) det( a, b, c ) = 0 3 = 0, y = det( a, d, c ) det( a, b, c ) = 1 3 = 1 3, z = det( a, b, d ) det( a, b, c ) = 1 3 =
12 Unidade 15 Operações com matrizes é a única solução do sistema Operações com matrizes a 1 b 1 c 1 m 1 n 1 p 1 Sejam A = a 2 b 2 c 2 e B = m 2 n 2 p 2 duas matrizes 3 3. a 3 b 3 c 3 m 3 n 3 p 3 Denimos a soma A+B das matrizes A e B e a multiplicação λa da matriz A por um número real λ de maneira análoga à soma de vetores e à multiplicação de um vetor por um escalar. A saber, a 1 + m 1 b 1 + n 1 c 1 + p 1 λa 1 λb 1 λc 1 A + B = a 2 + m 2 b 2 + n 2 c 2 + p 2 e λa = λa 2 λb 2 λc 2. a 3 + m 3 b 3 + n 3 c 3 + p 3 λa 3 λb 3 λc 3 Estas operações possuem as mesmas propriedades das operações com vetores, sendo a matriz nula O, matriz com todos os seus elementos iguais a zero, o elemento neutro da adição. Estendendo a denição de multiplicação de matrizes 2 2 vista no Capítulo 8, denimos a matriz produto AB da matriz A pela matriz B como sendo a matriz 3 3: a 1 m 1 + b 1 m 2 + c 1 m 3 a 1 n 1 + b 1 n 2 + c 1 n 3 a 1 p 1 + b 1 p 2 + c 1 p 3 AB= a 2 m 1 + b 2 m 2 + c 2 m 3 a 2 n 1 + b 2 n 2 + c 2 n 3 a 2 p 1 + b 2 p 2 + c 2 p 3 (15.4) a 3 m 1 + b 3 m 2 + c 3 m 3 a 3 n 1 + b 3 n 2 + c 3 n 3 a 3 p 1 + b 3 p 2 + c 3 p 3 Assim, o ij ésimo elemento da matriz produto AB é o produto interno do i ésimo vetor linha da matriz A pelo j ésimo vetor coluna da matriz B. Exemplo Se A = e B = 0 3 1, temos que AB é
13 Produto Misto, Determinante e Volume Unidade ( 1) ( 1) ( 1) = Sejam u, v e w três vetores no espaço. A matriz de Gram dos vetores u, v e w é a matriz 3 3 G( u, v, u, u u, v u, w w ) = v, u v, v v, w w, u w, v w,. w Se u = (a 1, b 1, c 1 ), v = (a 2, b 2, c 2 ) e w = (a 3, b 3, c 3 ) são os vetores num sistema de eixos ortogonais OXY Z e A a matriz cujos vetores linha são u, v e w, temos, pela denição do produto de matrizes, que AA T = G( u, v, w ). Como, pela propriedade (9) de determinante, det A = det A T, segue que (det A) 2 = det G( u, v, w ). Então, se u, v e w são linearmente independentes, obtemos que Exemplo 8 (Vol (P)) 2 = det G( u, v, w ), onde P é o paralelepípedo cujas arestas adjacentes são representantes dos vetores u, v e w. Neste caso, det G( u, v, w ) = (det A) 2 é um número positivo. Por exemplo, se AB, AC e AD são lados adjacentes do paralelepípedo P tais que AB = 2, AC = 3, AD = 1, ( AB, AC ) = 30 o, ( AB, AD ) = 45 o e ( AC, AD ) = 60 o, então ou seja, AB 2 Vol (P) 2 = det AC, AB AD, AB AB, AC AC 2 AD, AC AB, AD AC, AD AD 2, cos 90 o 2 1 cos 45 o Vol (P) 2 = det 2 3 cos 30 o cos 60 o, 2 1 cos 45 o 3 1 cos 60 o 1 13
14 Unidade 15 Operações com matrizes Vol (P) 2 = det /2. 2 3/2 1 Desenvolvendo o determinante segundo os elementos da primeira linha, obtemos Vol (P) 2 = 4 9 3/2 3/ / /2 = 4(9 9/2) 3 3( /2) + 2(9 3/2 9 2) = / /2 18 = 9( 6 1). Assim, Vol (P) = 3( 6 1). O produto de duas matrizes é associativo: (AB) C = A (BC); é distributivo: (A+B)C = AC +BC e A(B +C) = AB +AC, e o elemento neutro do produto é a matriz identidade: AI = IA = A. Mas o produto AB não é comutativo. Exemplo 9 Se A e B são as matrizes do exemplo 7, temos AB BA, pois BA = = Apesar do produto de matrizes não ser comutativo, temos det(ab) = det(ba), pois, pela proposição a seguir, det(ab) = det A det B = det B det A = det BA. Proposição 2 O determinante da matriz produto AB é igual ao produto do determinante da matriz A pelo determinante da matriz B. Ou seja, det AB = det A det B. Demonstração Por 15.4, o primeiro, o segundo e o terceiro vetores linha da matriz produto AB são dados, respectivamente, por: w 1 = a 1u1 w 2 = a 2u1 + b 1u2 + b 2u2 + c 1u3 + c 2u3 w 3 = a 3u1 + b 3u2 + c 3u3 14
15 Produto Misto, Determinante e Volume Unidade 15 onde u 1 linha da matriz B. = (m 1, n 1, p 1 ), u 2 = (m 2, n 2, p 2 ) e u 3 Pelas propriedades (1) e (2) do determinante, temos: det(ab) = det( w 1, w 2, w 3 ) Por outro lado, = det(a 1u1 + b 1u2 = (m 3, n 3, p 3 ) são os vetores + c 1 u3, w 2, w 3 ) = a 1 det( u 1, w 2, w 3 ) + b 1 det( u 2, w 2, w 3 ) +c 1 det( u 3, w 2, w 3 ). (15.5) det( u 1, w 2, w 3 ) = det( u 1, a 2u1 + b 2u2 + c 2u3, w 3 ) = a 2 det( u 1, u 1, w 3 ) + b 2 det( u 1, u 2, w 3 ) +c 2 det( u 1, u 3, w 3 ) = b 2 det( u 1, u 2, w 3 ) + c 2 det( u 1, u 3, w 3 ) (15.6) pois, pela propriedade (5) do determinante, det( u 1, u 1, w 3 ) = 0. E, sendo w 3 = a 3u1 + b 3u2 + c 3u3, temos e det( u 1, u 2, w 3 ) = det( u 1, u 2, a 3u1 + b 3u2 + c 3u3 ) = c 3 det( u 1, u 2, u 3 ) = c 3 det B, (15.7) det( u 1, u 3, w 3 ) = det( u 1, u 3, a 3u1 + b 3u2 + c 3u3 ) = b 3 det( u 1, u 3, u 2 ) = b 3 det B, (15.8) pois, pela propriedade (4) do determinante, det( u 1, u 3, u 2 ) = det( u 1, u 2, u 3 ). Logo, por 15.6, 15.7 e 15.8, det( u 1, w 2, w 3 ) = b 2 c 3 det B b 3 c 2 det B = (b 2 c 3 b 3 c 2 ) det B. (15.9) De modo análogo, podemos mostrar que det( u 2, w 2, w 3 ) = (a 3 c 2 a 2 c 3 ) det B, (15.10) 15
16 Unidade 15 Operações com matrizes e det( u 3, w 2, w 3 ) = (a 2 b 3 a 3 b 2 ) det B. (15.11) Concluímos, então, por 15.5, 15.9, e 15.11, que det(ab) = (a 1 (b 2 c 3 b 3 c 2 ) b 1 (a 2 c 3 a 3 c 2 ) + c 1 (a 2 b 3 a 3 b 2 )) det B = det A det B. Se O é a matriz nula, então OA = AO. Mas, o produto de duas matrizes não nulas não é necessariamente uma matriz não nula: A O e B O não implica que AB O. Exemplo Sejam as matrizes não nulas A = e B = É fácil vericar que AB = O. Outra diferença entre o produto de matrizes e o produto de números reais é que dada uma matriz A não nula do tipo 3 3 pode não existir uma matriz B tal que AB = BA = I. Quando uma tal matriz B existir, dizemos que A é invertível e B é a matriz inversa de A. A matriz inversa de uma matriz A, caso exista, é única. Com efeito, se AB = BA = I e AC = CA = I, então C = C I = C(AB) = (CA)B = I B = B. Escrevemos, então, B = A 1. Proposição 3 B = A 1. Sejam A e B matrizes 3 3 tais que AB = I. Então, BA = I, ou seja, Demonstração Sendo BA = I, temos, pela proposição 2, que det A det B = det(ab) = det I = 1. Logo, det A 0. Portanto, os vetores coluna da matriz A, v 1 = (a 1, a 2, a 3 ), v 2 = (b 1, b 2, b 3 ) e v 3 = (c 1, c 2, c 3 ), são, pela propriedade (10) do determinante, linearmente independentes. que: Assim, para todo vetor d = (d 1, d 2, d 3 ), existe um único vetor (x, y, z) tal x v 1 + y v 2 + z v 3 = d. 16
17 Produto Misto, Determinante e Volume Unidade 15 Ou equivalentemente, o sistema de três equações lineares a três incógnitas, a 1 x + b 1 y + c 1 z = d 1 a 2 x + b 2 y + c 3 z = d 2 (15.12) a 3 x + b 3 y + c 3 z = d 3 possui uma e apenas uma solução (x, y, z) para quaisquer números reais d 1, d 2 e d 3. Sejam v 1 = (x 1, y 1, z 1 ), v 2 = (x 2, y 2, z 2 ) e v 3 = (x 3, y 3, z 3 ) as soluções do sistema 15.12, para d = e 1 = (1, 0, 0), d = e 2 = (0, 1, 0) e d = e 3 = (0, 0, 1), respectivamente. Então, se C é a matriz cujos vetores coluna são v 1, v 2 e v 3, obtemos que AC = I. Além disso, como BA = I, temos B = B I = B(AC) = (BA)C = I C = C. Provamos que se BA = I, então AB = I, ou seja, B é a inversa da matriz A. Uma matriz A é ortogonal se AA T = I, ou seja, se sua inversa é a sua transposta. Pelo exemplo 8, A é ortogonal se, e somente se, a matriz de Gram dos vetores linha da matriz A é a matriz identidade. Assim, A é ortogonal se, e só se, seus vetores linha são ortonormais. Como, pela proposição 3, A T A = I, temos que A é uma matriz ortogonal se, e só se, seus vetores coluna são ortogonais. Exemplo 11 Encontre a terceira coluna da matriz 1/3 2/3 x A = 2/3 1/3 y, 2/3 2/3 z de modo que a matriz A seja ortogonal e det A > 0. Solução. Sejam v 1 = (1/3, 2/3, 2/3), v 2 = ( 2/3, 1/3, 2/3) o primeiro e o segundo vetores coluna da matriz. Como v 1 = v 2 = 1 e v 1, v 2 = 0, a matriz A é ortogonal se, e só se, o terceiro vetor coluna v 3 unitário e ortogonal aos vetores u 1 e u 2. = (x, y, z) é Exemplo 12 17
18 Unidade 15 Operações com matrizes Basta, então, tomar v 3 = (x, y, z) = ±( v 1 v 2 ) ( ) 2/3 = ± 1/3 2/3, 1/3 2/3 2/3, 1/3 2/3 2/3 1/3 v 3 = (x, y, z) = ±(6/9, 6/9, 3/9) = ±(2/3, 2/3, 1/3). Sendo det A > 0, devemos tomar v 3 = v 1 v 2, pois det( v 1, v 2, v 1 v 2 ) = v 1 v 2, v 1 v 2 > 0. A identidade AB = I signica que os vetores coluna (x 1, y 1, z 1 ), (x 2, y 2, z 2 ) e (x 3, y 3, z 3 ) da matriz B são as únicas soluções dos sistemas: a 1 x 1 + b 1 y 1 + c 1 z 1 = 1 a 1 x 2 + b 1 y 2 + c 1 z 2 = 0 a 2 x 1 + b 2 y 1 + c 3 z 1 = 0, a 2 x 2 + b 2 y 2 + c 3 z 2 = 1 a 3 x 1 + b 3 y 1 + c 3 z 1 = 0 a 3 x 2 + b 3 y 2 + c 3 z 2 = 0 a 1 x 3 + b 1 y 3 + c 1 z 3 = 0 a 2 x 3 + b 2 y 3 + c 3 z 3 = 0. a 3 x 3 + b 3 y 3 + c 3 z 3 = 1, Pela regra de Cramer, aplicada a cada um dos sistemas acima, segue que x 1 = det( e 1, b, c ) det A x 2 = det( e 2, b, c ) det A x 3 = det( e 3, b, c ) det A, y 1 = det( a, e 1, c ) det A, y 2 = det( a, e 2, c ) det A, y 3 = det( a, e 3, c ) det A, z 1 = det( a, b, e 1 ), det A, z 2 = det( a, b, e 2 ), det A, z 3 = det( a, b, e 3 ), det A onde a = (a 1, a 2, a 3 ), b = (b 1, b 2, b 3 ) e c = (c 1, c 2, c 3 ) são os vetores coluna da matriz A. Logo, como det( e 1, b, c ) = A 11, det( a, e 1, c ) = A 12, det( a, b, e 1 ) = A 13, det( e 2, b, c ) = A 21, det( a, e 2, c ) = A 22, det( a, b, e 2 ) = A 23, det( e 3, b, c ) = A 31, det( a, e 3, c ) = A 32, det( a, b, e 3 ) = A 33, obtemos: 18
19 Produto Misto, Determinante e Volume Unidade 15 x 1 = ( 1)1+1 A 11 det A, y 1 = ( 1)1+2 A 12 det A, z 1 = ( 1)1+3 A 13 det A, x 2 = ( 1)2+1 A 21 det A, y 2 = ( 1)2+2 A 22 det A, z 2 = ( 1)2+3 A 23 det A, x 3 = ( 1)3+1 A 31 det A, y 3 = ( 1)3+2 A 32 det A, z 3 = ( 1)3+3 A 33 det A, onde A ij, i, j = 1, 2, 3, é o ij ésimo menor da matriz A. Portanto, a matriz inversa da matriz A é A 1 = 1 ( 1) 1+1 A 11 ( 1) 2+1 A 21 ( 1) 3+1 A 31 ( 1) 1+2 A det A 12 ( 1) 2+2 A 22 ( 1) 3+2 A 32 ( 1) 1+3 A 13 ( 1) 2+3 A 23 ( 1) 3+3 A Se a A = 2 3 1, então A 11 = = 7, A 12 = = 3, A 13 = = 5, A 21 = = 6, A 22 = = 2, A 23 = = 2, A 31 = = 1, A 32 = = 1, A 33 = = 1, logo, o determinante da matriz A é det A = ( 1) A 11 + ( 1) A 12 + ( 1) A 13 = = 4, e a sua inversa é A 1 = Exemplo 13 Pelos resultados obtidos ao longo deste capítulo, podemos vericar, com facilidade, que as seguintes armações a respeito de uma matriz A, com vetores linha (a 1, b 1, c 1 ), (a 2, b 2, c 2 ) e (a 3, b 3, c 3 ), são equivalentes: 1. Os vetores linha da matriz A são L.I.. 2. O determinante da matriz A é diferente de zero. 3. Os vetores coluna da matriz A são L.I.. 4. O sistema de três equações lineares, 19
20 Unidade 15 Operações com matrizes a 1 x + b 1 y + c 1 z = d 1 a 2 x + b 2 y + c 3 z = d 2 a 3 x + b 3 y + c 3 z = d 3, possui uma e apenas uma solução para cada (d 1, d 2, d 3 ) R A matriz A é invertível. Todas as denições e resultados deste capítulo, envolvendo matrizes e determinante, continuam válidos para matrizes n n, onde n é um número natural maior ou igual a 2. 20
21 Produto Misto, Determinante e Volume Unidade Exercícios 1. Determine para quais valores de m R o paralelepípedo P de vértices A = (1, 1, 1), B = (2, 3, 4), C = (5, 2, 1) e D = (1, 2, m) tem volume igual a Considere as matrizes 3 3 abaixo: A = 4 2 3, B = 6 1 3, C = Calcule o determinante da: (a) matriz A, desenvolvendo-o pela primeira linha e pela segunda coluna. (b) matriz B, desenvolvendo-o pela segunda linha e pela terceira coluna. (c) matriz C, desenvolvendo-o pela terceira linha e pela segunda coluna. 3. Verique que os sistemas têm uma única solução e encontre a solução, usando a regra de Cramer: x + 2y z = 1 (a) x + 3y + 2z = 3 2x y + z = 2 2x + y 3z = 5 (b) 2y + z = 0 4x + 3y + 2z = 7 Resolva também os sistemas colocando uma variável em função das outras e substituindo essa variável nas equações para obter um sistema de duas equações lineares a duas incógnitas. Qual é o método mais prático?. 4. Obtenha a matriz E = (A + 3B)(2C 5D), onde A = 2 0 1, B = 1 3 1, C = 1 2 3, D = Prove que se A, B e C são matrizes 3 3, então (AB)C = A(BC), A(B + C) = AB + AC e (A + B)C = AC + BC. 21
22 Unidade 15 Exercícios 6. Considere as matrizes: 0 x y x y + z 1 A = x 0 z e B = y x + z 1. y z 0 z x + y 1 Escreva uma linha das matrizes acima como combinação linear das outras linhas e também uma coluna como combinação das demais colunas. Conclua que det A = 0 e det B = 0 para quaisquer x, y, z R. 7. Verique quais matrizes do exercício 2 são invertíveis. Neste caso, encontre sua inversa. 8. Determine o vetor (x, y, z) de modo que a matriz A seja ortogonal e det A < 0, onde 1/ 3 1/ 3 1/ 3 A = x y z 1/ 6 2/ 6 1/ Seja P o paralelogramo no plano com vértices nos pontos A = (x 0, y 0 ), B = (x 1, y 1 ) e C = (x 2, y 2 ). Prove que x 0 y 0 1 Área P = det x 1 y 1 1. x 2 y Um sistema é homogêneo se é da forma: a 1 x + b 1 y + c 1 z = 0 a 2 x + b 2 y + c 2 z = 0 a 3 x + b 3 y + c 3 z = 0 Mostre que os vetores (a 1, b 1, c 1 ), (a 2, b 2, c 2 ) e (a 3, b 3, c 3 ) são L.I. se, e somente se, x = y = z = 0 é a única solução do sistema. 11. Verique que o determinante da matriz x y z x 2 y 2 z 2 é (z y)(z x)(y x). Conclua que as linhas da matriz são LI, se e somente se, x, y e z são três números reais distintos. Uma matriz da forma acima é chamada matriz de Vandermonde do tipo
23 Produto Misto, Determinante e Volume Unidade Sejam A e B duas matrizes 3 3. Prove que (AB) T = B T A T e conclua que se A é invertível, então A T é invertível e (A T ) 1 = (A 1 ) T. 13. Sejam A e B duas matrizes 3 3, sendo B invertível. Prove as armações abaixo: (a) det(λa) = λ 3 det A, para todo λ R. (b) det B 1 = 1 det B. (c) (B 1 ) 1 = B. (d) det(b 1 AB) = det A. (e) det(b T AB) = det A, se B é ortogonal. (f) (B 1 AB) n = B 1 A n B, para todo n N. (g) Se B é ortogonal, então det B = ±1. (h) Se A 2 = O, então A não é invertível. a 1 b 1 c Seja A = a 2 b 2 c 2 uma matriz do tipo 3 3. O traço da matriz A é a 3 b 3 c 3 o número: Tr(A) = a 1 + b 2 + c 3. Mostre que: (a) Tr(AB) = Tr(BA). (b) Tr(C 1 AC) = Tr(A), se C é invertível. (c) Tr(D T AD) = Tr(A), se D é ortogonal. (d) (Tr A T ) 2 3 Tr(AA T ) e a igualdade ocorre se, e só se, existe λ R tal que A = λi. 15. Seja A uma matriz 3 3 cujos vetores linha u, v e w. Prove que det A u v w, e a igualdade acontece se, e só se, ortogonais. Interprete geometricamente este resultado. u, v e w são vetores dois a dois 23
Produto interno e produto vetorial no espaço
 14 Produto interno e produto vetorial no espaço Sumário 14.1 Produto interno.................... 14. Produto vetorial.................... 5 14..1 Interpretação geométrica da norma do produto vetorial.......................
14 Produto interno e produto vetorial no espaço Sumário 14.1 Produto interno.................... 14. Produto vetorial.................... 5 14..1 Interpretação geométrica da norma do produto vetorial.......................
Equação Geral do Segundo Grau em R 2
 8 Equação Geral do Segundo Grau em R Sumário 8.1 Introdução....................... 8. Autovalores e autovetores de uma matriz real 8.3 Rotação dos Eixos Coordenados........... 5 8.4 Formas Quadráticas..................
8 Equação Geral do Segundo Grau em R Sumário 8.1 Introdução....................... 8. Autovalores e autovetores de uma matriz real 8.3 Rotação dos Eixos Coordenados........... 5 8.4 Formas Quadráticas..................
MAT3457 ÁLGEBRA LINEAR PARA ENGENHARIA I 1 a Lista de Exercícios - 1 o semestre de 2018
 MAT3457 ÁLGEBRA LINEAR PARA ENGENHARIA I a Lista de Exercícios - o semestre de 8 Exercícios -8: os espaços V e V 3. Exercícios 9-7: dependência, independência linear, bases. Exercícios 8-48: sistemas lineares.
MAT3457 ÁLGEBRA LINEAR PARA ENGENHARIA I a Lista de Exercícios - o semestre de 8 Exercícios -8: os espaços V e V 3. Exercícios 9-7: dependência, independência linear, bases. Exercícios 8-48: sistemas lineares.
Capítulo Propriedades das operações com vetores
 Capítulo 6 1. Propriedades das operações com vetores Propriedades da adição de vetores Sejam u, v e w vetores no plano. Valem as seguintes propriedades. Comutatividade: u + v = v + u. Associatividade:
Capítulo 6 1. Propriedades das operações com vetores Propriedades da adição de vetores Sejam u, v e w vetores no plano. Valem as seguintes propriedades. Comutatividade: u + v = v + u. Associatividade:
I Lista de Álgebra Linear /02 Matrizes-Determinantes e Sistemas Prof. Iva Zuchi Siple
 1 I Lista de Álgebra Linear - 2012/02 Matrizes-Determinantes e Sistemas Prof. Iva Zuchi Siple 1. Determine os valores de x e y que tornam verdadeira a igualdade ( x 2 + 5x x 2 ( 6 3 2x y 2 5y y 2 = 5 0
1 I Lista de Álgebra Linear - 2012/02 Matrizes-Determinantes e Sistemas Prof. Iva Zuchi Siple 1. Determine os valores de x e y que tornam verdadeira a igualdade ( x 2 + 5x x 2 ( 6 3 2x y 2 5y y 2 = 5 0
Aula Orientação do espaço. Observação 1
 Aula 14 Nesta aula vamos definir dois novos produtos entre vetores do espaço, o produto vetorial e o produto misto. Para isso, primeiro vamos apresentar o conceito de orientação. 1. Orientação do espaço
Aula 14 Nesta aula vamos definir dois novos produtos entre vetores do espaço, o produto vetorial e o produto misto. Para isso, primeiro vamos apresentar o conceito de orientação. 1. Orientação do espaço
O Plano no Espaço. Sumário
 17 Sumário 17.1 Introdução....................... 2 17.2 Equações paramétricas do plano no espaço..... 2 17.3 Equação cartesiana do plano............. 15 17.4 Exercícios........................ 21 1 Unidade
17 Sumário 17.1 Introdução....................... 2 17.2 Equações paramétricas do plano no espaço..... 2 17.3 Equação cartesiana do plano............. 15 17.4 Exercícios........................ 21 1 Unidade
Aula 4 Colinearidade, coplanaridade e dependência linear
 Aula 4 Colinearidade, coplanaridade e dependência linear MÓDULO 1 - AULA 4 Objetivos Compreender os conceitos de independência e dependência linear. Estabelecer condições para determinar quando uma coleção
Aula 4 Colinearidade, coplanaridade e dependência linear MÓDULO 1 - AULA 4 Objetivos Compreender os conceitos de independência e dependência linear. Estabelecer condições para determinar quando uma coleção
Capítulo 1. Matrizes e Sistema de Equações Lineares. 1.1 Corpos
 Capítulo 1 Matrizes e Sistema de Equações Lineares Neste capítulo apresentaremos as principais de nições e resultados sobre matrizes e sistemas de equações lineares que serão necessárias para o desenvolvimento
Capítulo 1 Matrizes e Sistema de Equações Lineares Neste capítulo apresentaremos as principais de nições e resultados sobre matrizes e sistemas de equações lineares que serão necessárias para o desenvolvimento
1. Operações com vetores no espaço
 Capítulo 10 1. Operações com vetores no espaço Vamos definir agora as operações de adição de vetores no espaço e multiplicação de um vetor espacial por um número real. O processo é análogo ao efetuado
Capítulo 10 1. Operações com vetores no espaço Vamos definir agora as operações de adição de vetores no espaço e multiplicação de um vetor espacial por um número real. O processo é análogo ao efetuado
MAT2457 ÁLGEBRA LINEAR PARA ENGENHARIA I 1 a Lista de Exercícios - 1 o semestre de Resolva o sistema abaixo para as incógnitas x e y:
 MAT2457 ÁLGEBRA LINEAR PARA ENGENHARIA I 1 a Lista de Exercícios - 1 o semestre de 2015 1 Determine x em função de u e v na equação 2 x 3 u = 10( x + v 2 Resolva o sistema abaixo para as incógnitas x e
MAT2457 ÁLGEBRA LINEAR PARA ENGENHARIA I 1 a Lista de Exercícios - 1 o semestre de 2015 1 Determine x em função de u e v na equação 2 x 3 u = 10( x + v 2 Resolva o sistema abaixo para as incógnitas x e
determinantes rita simões departamento de matemática - ua
 determinantes rita simões (ritasimoes@ua.pt) departamento de matemática - ua 204-205 determinante de uma matriz sejam l,..., l n as linhas de uma matriz do tipo n n; para cada n N, existe uma única função
determinantes rita simões (ritasimoes@ua.pt) departamento de matemática - ua 204-205 determinante de uma matriz sejam l,..., l n as linhas de uma matriz do tipo n n; para cada n N, existe uma única função
Álgebra Linear e Geometria Anaĺıtica
 Álgebra Linear e Geometria Anaĺıtica 2016/17 MIEI+MIEB+MIEMN Slides da 4 a Semana de aulas Cláudio Fernandes (FCT/UNL) Departamento de Matemática 1 / 27 Programa 1 Matrizes 2 Sistemas de Equações Lineares
Álgebra Linear e Geometria Anaĺıtica 2016/17 MIEI+MIEB+MIEMN Slides da 4 a Semana de aulas Cláudio Fernandes (FCT/UNL) Departamento de Matemática 1 / 27 Programa 1 Matrizes 2 Sistemas de Equações Lineares
MAT2457 ÁLGEBRA LINEAR PARA ENGENHARIA I 1 a Prova - 1 o semestre de y + az = a (a 2)x + y + 3z = 0 (a 1)y = 1 a
 MAT457 ÁLGEBRA LINEAR PARA ENGENHARIA I 1 a Prova - 1 o semestre de 018 Questão 1. Se a R, é correto afirmar que o sistema linear y + az = a (a x + y + 3z = 0 (a 1y = 1 a é: (a possível e indeterminado
MAT457 ÁLGEBRA LINEAR PARA ENGENHARIA I 1 a Prova - 1 o semestre de 018 Questão 1. Se a R, é correto afirmar que o sistema linear y + az = a (a x + y + 3z = 0 (a 1y = 1 a é: (a possível e indeterminado
23 e 24. Forma Quadrática e Equação do Segundo Grau em R 3. Sumário
 23 e 24 Forma Quadrática e Equação do Segundo Grau em R 3 Sumário 23.1 Introdução....................... 2 23.2 Autovalores e Autovetores de uma matriz 3 3.. 2 23.3 Mudança de Coordenadas no Espaço........
23 e 24 Forma Quadrática e Equação do Segundo Grau em R 3 Sumário 23.1 Introdução....................... 2 23.2 Autovalores e Autovetores de uma matriz 3 3.. 2 23.3 Mudança de Coordenadas no Espaço........
Sistemas de equações lineares com três variáveis
 18 Sistemas de equações lineares com três variáveis Sumário 18.1 Introdução....................... 18. Sistemas de duas equações lineares........... 18. Sistemas de três equações lineares........... 8
18 Sistemas de equações lineares com três variáveis Sumário 18.1 Introdução....................... 18. Sistemas de duas equações lineares........... 18. Sistemas de três equações lineares........... 8
1 a Lista de Exercícios de MAT2457 Escola Politécnica 1 o semestre de (b)
 a Lista de Exercícios de MAT457 Escola Politécnica o semestre de 04 Resolva os seguintes sistemas: x + x x 3 + 3x 4 = a 3x + x x 3 + x 4 = 4 3x + 3x + 3x 3 3x 4 = 5 c x + x 3 + x 5 = x + x 3 + x 5 + x
a Lista de Exercícios de MAT457 Escola Politécnica o semestre de 04 Resolva os seguintes sistemas: x + x x 3 + 3x 4 = a 3x + x x 3 + x 4 = 4 3x + 3x + 3x 3 3x 4 = 5 c x + x 3 + x 5 = x + x 3 + x 5 + x
Parte 1 - Matrizes e Sistemas Lineares
 Parte 1 - Matrizes e Sistemas Lineares Matrizes: Uma matriz de tipo m n é uma tabela com mn elementos, denominados entradas, e formada por m linhas e n colunas. A matriz identidade de ordem 2, por exemplo,
Parte 1 - Matrizes e Sistemas Lineares Matrizes: Uma matriz de tipo m n é uma tabela com mn elementos, denominados entradas, e formada por m linhas e n colunas. A matriz identidade de ordem 2, por exemplo,
5. Considere os seguintes subconjuntos do espaço vetorial F(R) das funções de R em R:
 MAT3457 ÁLGEBRA LINEAR I 3 a Lista de Exercícios 1 o semestre de 2018 1. Verique se V = {(x, y) : x, y R} é um espaço vetorial sobre R com as operações de adição e de multiplicação por escalar dadas por:
MAT3457 ÁLGEBRA LINEAR I 3 a Lista de Exercícios 1 o semestre de 2018 1. Verique se V = {(x, y) : x, y R} é um espaço vetorial sobre R com as operações de adição e de multiplicação por escalar dadas por:
MAT2457 ÁLGEBRA LINEAR PARA ENGENHARIA I 2 a Lista de Exercícios - 1 o semestre de f 1 = 2 e 1 e 2 e 3,
 MAT2457 ÁLGEBRA LINEAR PARA ENGENHARIA I 2 a Lista de Exercícios - 1 o semestre de 2015 1 Sendo E = { e 1 e 2 e 3 } F = { f 1 f 2 f 3 } bases com: f 1 = 2 e 1 e 3 f 2 = e 2 + 2 e 3 f 3 = 7 e 3 e w = e
MAT2457 ÁLGEBRA LINEAR PARA ENGENHARIA I 2 a Lista de Exercícios - 1 o semestre de 2015 1 Sendo E = { e 1 e 2 e 3 } F = { f 1 f 2 f 3 } bases com: f 1 = 2 e 1 e 3 f 2 = e 2 + 2 e 3 f 3 = 7 e 3 e w = e
Lista de Exercícios 3 (Matrizes e Sistemas Lineares) b) B 4 2, tal que b ij =
 UNIVERSIDADE TECNOLÓGICA FEDERAL DO PARANÁ Departamento Acadêmico de Matemática - DAMAT Geometria Analítica e Álgebra Linear (MA71B) Profa. Dra. Nara Bobko Lista de Exercícios 3 (Matrizes e Sistemas Lineares)
UNIVERSIDADE TECNOLÓGICA FEDERAL DO PARANÁ Departamento Acadêmico de Matemática - DAMAT Geometria Analítica e Álgebra Linear (MA71B) Profa. Dra. Nara Bobko Lista de Exercícios 3 (Matrizes e Sistemas Lineares)
b) 4x 1 6x 2 = 1 Questão 2: Considere as seguintes matrizes: 3y 6 y z condições, calcule x, y e z.
 Ministério da Educação Universidade Tecnológica Federal do Paraná Campus Curitiba - DAMAT MA71B - Geometria Analítica e Álgebra Linear Prof a Dr a Diane Rizzotto Rossetto LISTA 1 - Matrizes e Sistemas
Ministério da Educação Universidade Tecnológica Federal do Paraná Campus Curitiba - DAMAT MA71B - Geometria Analítica e Álgebra Linear Prof a Dr a Diane Rizzotto Rossetto LISTA 1 - Matrizes e Sistemas
Aula 22 Produto vetorial, produto misto e volume
 Aula 22 Produto vetorial, produto misto e volume MÓDULO 2 - AULA 22 Objetivos Definir o produto misto de três vetores no espaço a partir do cálculo de volumes de paralelepípedos. Exprimir o produto vetorial
Aula 22 Produto vetorial, produto misto e volume MÓDULO 2 - AULA 22 Objetivos Definir o produto misto de três vetores no espaço a partir do cálculo de volumes de paralelepípedos. Exprimir o produto vetorial
MA71B - Geometria Analítica e Álgebra Linear Prof a Dr a Diane Rizzotto Rossetto. LISTA 1 - Matrizes e Sistemas Lineares
 Ministério da Educação Universidade Tecnológica Federal do Paraná Campus Curitiba - DAMAT MA71B - Geometria Analítica e Álgebra Linear Prof a Dr a Diane Rizzotto Rossetto LISTA 1 - Matrizes e Sistemas
Ministério da Educação Universidade Tecnológica Federal do Paraná Campus Curitiba - DAMAT MA71B - Geometria Analítica e Álgebra Linear Prof a Dr a Diane Rizzotto Rossetto LISTA 1 - Matrizes e Sistemas
Geometria Analítica e Álgebra Linear
 NOTAS DE AULA Geometria Analítica e Álgebra Linear Vetores no Espaço Professor: Luiz Fernando Nunes, Dr. 019/Sem_01 Índice Vetores no Espaço Tridimensional... 1.1 Definição... 1. Operações com vetores...
NOTAS DE AULA Geometria Analítica e Álgebra Linear Vetores no Espaço Professor: Luiz Fernando Nunes, Dr. 019/Sem_01 Índice Vetores no Espaço Tridimensional... 1.1 Definição... 1. Operações com vetores...
J. Delgado - K. Frensel - L. Crissaff Geometria Analítica e Cálculo Vetorial
 128 Capítulo 7 Coordenadas e distância no espaço 1. Coordenadas no Espaço Seja E o espaço da Geometria Euclidiana tridimensional. Um sistema de eixos ortogonais OXY Z em E consiste de três eixos ortogonais
128 Capítulo 7 Coordenadas e distância no espaço 1. Coordenadas no Espaço Seja E o espaço da Geometria Euclidiana tridimensional. Um sistema de eixos ortogonais OXY Z em E consiste de três eixos ortogonais
J. Delgado - K. Frensel - L. Crissaff Geometria Analítica e Cálculo Vetorial
 178 Capítulo 10 Equação da reta e do plano no espaço 1. Equações paramétricas da reta no espaço Sejam A e B dois pontos distintos no espaço e seja r a reta que os contém. Então, P r existe t R tal que
178 Capítulo 10 Equação da reta e do plano no espaço 1. Equações paramétricas da reta no espaço Sejam A e B dois pontos distintos no espaço e seja r a reta que os contém. Então, P r existe t R tal que
Neste módulo, não daremos a definição padrão de determinantes via somatório envolvendo sinais de permutações, pois não há necessidade de entrarmos em
 Neste módulo, não daremos a definição padrão de determinantes via somatório envolvendo sinais de permutações, pois não há necessidade de entrarmos em tantos detalhes para os concursos desejados. Assim,
Neste módulo, não daremos a definição padrão de determinantes via somatório envolvendo sinais de permutações, pois não há necessidade de entrarmos em tantos detalhes para os concursos desejados. Assim,
Matrizes Semelhantes e Matrizes Diagonalizáveis
 Diagonalização Matrizes Semelhantes e Matrizes Diagonalizáveis Nosso objetivo neste capítulo é estudar aquelas transformações lineares de R n para as quais existe pelo menos uma base em que elas são representadas
Diagonalização Matrizes Semelhantes e Matrizes Diagonalizáveis Nosso objetivo neste capítulo é estudar aquelas transformações lineares de R n para as quais existe pelo menos uma base em que elas são representadas
Vetores e Geometria Analítica
 Vetores e Geometria Analítica ECT2102 Prof. Ronaldo Carlotto Batista 23 de fevereiro de 2016 AVISO O propósito fundamental destes slides é servir como um guia para as aulas. Portanto eles não devem ser
Vetores e Geometria Analítica ECT2102 Prof. Ronaldo Carlotto Batista 23 de fevereiro de 2016 AVISO O propósito fundamental destes slides é servir como um guia para as aulas. Portanto eles não devem ser
MA71B - Geometria Analítica e Álgebra Linear Prof a Dr a Diane Rizzotto Rossetto. LISTA 1 - Matrizes e Sistemas Lineares
 Ministério da Educação Universidade Tecnológica Federal do Paraná Campus Curitiba - DAMAT MA71B - Geometria Analítica e Álgebra Linear Prof a Dr a Diane Rizzotto Rossetto LISTA 1 - Matrizes e Sistemas
Ministério da Educação Universidade Tecnológica Federal do Paraná Campus Curitiba - DAMAT MA71B - Geometria Analítica e Álgebra Linear Prof a Dr a Diane Rizzotto Rossetto LISTA 1 - Matrizes e Sistemas
ÁLGEBRA LINEAR I - MAT0032
 UNIVERSIDADE FEDERAL DA INTEGRAÇÃO LATINO-AMERICANA Instituto Latino-Americano de Ciências da Vida e Da Natureza Centro Interdisciplinar de Ciências da Natureza ÁLGEBRA LINEAR I - MAT003 10 a Lista de
UNIVERSIDADE FEDERAL DA INTEGRAÇÃO LATINO-AMERICANA Instituto Latino-Americano de Ciências da Vida e Da Natureza Centro Interdisciplinar de Ciências da Natureza ÁLGEBRA LINEAR I - MAT003 10 a Lista de
UNIVERSIDADE FEDERAL DO CEARÁ CENTRO DE TECNOLOGIA PROGRAMA DE EDUCAÇÃO TUTORIAL SOLUCIONÁRIO DE ÁLGEBRA. Realização:
 UNIVERSIDADE FEDERAL DO CEARÁ CENTRO DE TECNOLOGIA PROGRAMA DE EDUCAÇÃO TUTORIAL SOLUCIONÁRIO APOSTILA DE ÁLGEBRA Realização: 2012 1. Matrizes 1.3. Questões 1. A = e B = AB = = = BA = = = 2. A = B, tal
UNIVERSIDADE FEDERAL DO CEARÁ CENTRO DE TECNOLOGIA PROGRAMA DE EDUCAÇÃO TUTORIAL SOLUCIONÁRIO APOSTILA DE ÁLGEBRA Realização: 2012 1. Matrizes 1.3. Questões 1. A = e B = AB = = = BA = = = 2. A = B, tal
Matrizes e sistemas de equações algébricas lineares
 Capítulo 1 Matrizes e sistemas de equações algébricas lineares ALGA 2007/2008 Mest Int Eng Biomédica Matrizes e sistemas de equações algébricas lineares 1 / 37 Definições Equação linear Uma equação (algébrica)
Capítulo 1 Matrizes e sistemas de equações algébricas lineares ALGA 2007/2008 Mest Int Eng Biomédica Matrizes e sistemas de equações algébricas lineares 1 / 37 Definições Equação linear Uma equação (algébrica)
GAAL - Exame Especial - 12/julho/2013. Questão 1: Considere os pontos A = (1, 2, 3), B = (2, 3, 1), C = (3, 1, 2) e D = (2, 2, 1).
 GAAL - Exame Especial - /julho/3 SOLUÇÕES Questão : Considere os pontos A = (,, 3), B = (, 3, ), C = (3,, ) e D = (,, ) (a) Chame de α o plano que passa pelos pontos A, B e C e de β o plano que passa pelos
GAAL - Exame Especial - /julho/3 SOLUÇÕES Questão : Considere os pontos A = (,, 3), B = (, 3, ), C = (3,, ) e D = (,, ) (a) Chame de α o plano que passa pelos pontos A, B e C e de β o plano que passa pelos
Lista 3 com respostas
 Lista 3 com respostas Professora Nataliia Goloshchapova MAT0105-1 semestre de 2018 Exercício 1. Sendo que w = ( u v) ( u + v), determine o ângulo entre os vetores u e v, sabendo que u = v = w = 1 e u v
Lista 3 com respostas Professora Nataliia Goloshchapova MAT0105-1 semestre de 2018 Exercício 1. Sendo que w = ( u v) ( u + v), determine o ângulo entre os vetores u e v, sabendo que u = v = w = 1 e u v
Notas de Aulas de Matrizes, Determinantes e Sistemas Lineares
 FATEC Notas de Aulas de Matrizes, Determinantes e Sistemas Lineares Prof Dr Ânderson Da Silva Vieira 2017 Sumário Introdução 2 1 Matrizes 3 11 Introdução 3 12 Tipos especiais de Matrizes 3 13 Operações
FATEC Notas de Aulas de Matrizes, Determinantes e Sistemas Lineares Prof Dr Ânderson Da Silva Vieira 2017 Sumário Introdução 2 1 Matrizes 3 11 Introdução 3 12 Tipos especiais de Matrizes 3 13 Operações
exercícios de álgebra linear 2016
 exercícios de álgebra linear 206 maria irene falcão :: maria joana soares Conteúdo Matrizes 2 Sistemas de equações lineares 7 3 Determinantes 3 4 Espaços vetoriais 9 5 Transformações lineares 27 6 Valores
exercícios de álgebra linear 206 maria irene falcão :: maria joana soares Conteúdo Matrizes 2 Sistemas de equações lineares 7 3 Determinantes 3 4 Espaços vetoriais 9 5 Transformações lineares 27 6 Valores
ÁLGEBRA LINEAR - MAT0024
 UNIVERSIDADE FEDERAL DA INTEGRAÇÃO LATINO-AMERICANA Instituto Latino-Americano de Ciências da Vida e Da Natureza Centro Interdisciplinar de Ciências da Natureza ÁLGEBRA LINEAR - MAT0024 10 a Lista de exercícios
UNIVERSIDADE FEDERAL DA INTEGRAÇÃO LATINO-AMERICANA Instituto Latino-Americano de Ciências da Vida e Da Natureza Centro Interdisciplinar de Ciências da Natureza ÁLGEBRA LINEAR - MAT0024 10 a Lista de exercícios
Dependência linear e bases
 Dependência linear e bases Sadao Massago 2014 Sumário 1 Dependência linear 1 2 ases e coordenadas 3 3 Matriz mudança de base 5 Neste texto, introduziremos o que é uma base do plano ou do espaço 1 Dependência
Dependência linear e bases Sadao Massago 2014 Sumário 1 Dependência linear 1 2 ases e coordenadas 3 3 Matriz mudança de base 5 Neste texto, introduziremos o que é uma base do plano ou do espaço 1 Dependência
Álgebra Linear I - Aula 14. Roteiro
 Álgebra Linear I - Aula 14 1 Matrizes 2 Forma matricial de uma transformação linear 3 Composição de transformações lineares e produto de matrizes 4 Determinante do produto de matrizes Roteiro 1 Matrizes
Álgebra Linear I - Aula 14 1 Matrizes 2 Forma matricial de uma transformação linear 3 Composição de transformações lineares e produto de matrizes 4 Determinante do produto de matrizes Roteiro 1 Matrizes
linearmente independentes se e somente se: Exercícios 13. Determine o vetor X, tal que 3X-2V = 15(X - U).
 11 linearmente independentes se e somente se: 1.4. Exercícios 1. Determine o vetor X, tal que X-2V = 15(X - U). Figura 21 14. Determine os vetores X e Y tais que: 1.4.2 Multiplicação por um escalar. Se
11 linearmente independentes se e somente se: 1.4. Exercícios 1. Determine o vetor X, tal que X-2V = 15(X - U). Figura 21 14. Determine os vetores X e Y tais que: 1.4.2 Multiplicação por um escalar. Se
GAAL Exercícios 6: Umas soluções
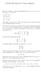 GAAL Exercícios 6: Umas soluções. Quais dos seguintes vetores são combinação linear de u = (5, 3, ), v = (, 4, 3), w = (, 8, 7)? (a) (, 2, 5) (b) (, 2, 8) (c) ( 2, ) (d) (, 2, 3). O conjunto {u, v, w}
GAAL Exercícios 6: Umas soluções. Quais dos seguintes vetores são combinação linear de u = (5, 3, ), v = (, 4, 3), w = (, 8, 7)? (a) (, 2, 5) (b) (, 2, 8) (c) ( 2, ) (d) (, 2, 3). O conjunto {u, v, w}
Lista 3 com respostas
 Lista 3 com respostas Professora Nataliia Goloshchapova MAT0105-1 semestre de 2019 Exercício 1. Sendo que w = ( u v) ( u + v), determine o ângulo entre os vetores u e v, sabendo que u = v = w = 1 e u v
Lista 3 com respostas Professora Nataliia Goloshchapova MAT0105-1 semestre de 2019 Exercício 1. Sendo que w = ( u v) ( u + v), determine o ângulo entre os vetores u e v, sabendo que u = v = w = 1 e u v
Fundamentos de Matemática Curso: Informática Biomédica
 Fundamentos de Matemática Curso: Informática Biomédica Profa. Vanessa Rolnik Artioli Assunto: determinantes e sistemas 13 e 27/06/14 Determinantes Def.: Seja M uma matriz quadrada de elementos reais, de
Fundamentos de Matemática Curso: Informática Biomédica Profa. Vanessa Rolnik Artioli Assunto: determinantes e sistemas 13 e 27/06/14 Determinantes Def.: Seja M uma matriz quadrada de elementos reais, de
1 Vetores no Plano e no Espaço
 1 Vetores no Plano e no Espaço Definimos as componentes de um vetor no espaço de forma análoga a que fizemos com vetores no plano. Vamos inicialmente introduzir um sistema de coordenadas retangulares no
1 Vetores no Plano e no Espaço Definimos as componentes de um vetor no espaço de forma análoga a que fizemos com vetores no plano. Vamos inicialmente introduzir um sistema de coordenadas retangulares no
MAT2457 ÁLGEBRA LINEAR PARA ENGENHARIA I Gabarito da 2 a Prova - 1 o semestre de 2015
 MAT27 ÁLGEBRA LINEAR PARA ENGENHARIA I Gabarito da 2 a Prova - 1 o semestre de 201 Nesta prova considera-se fixada uma orientação do espaço e um sistema de coordenadas Σ (O, E) em E 3, em que E é uma base
MAT27 ÁLGEBRA LINEAR PARA ENGENHARIA I Gabarito da 2 a Prova - 1 o semestre de 201 Nesta prova considera-se fixada uma orientação do espaço e um sistema de coordenadas Σ (O, E) em E 3, em que E é uma base
Hewlett-Packard DETERMINANTE. Aulas 01 a 05. Elson Rodrigues, Gabriel Carvalho e Paulo Luiz
 Hewlett-Packard DETERMINANTE Aulas 0 a 05 Elson Rodrigues, Gabriel Carvalho e Paulo Luiz Sumário DETERMINANTE... Exemplo... Exemplo...... Exemplo...... TEOREMA DE LAPLACE... I) COFATOR... Exemplo... II)
Hewlett-Packard DETERMINANTE Aulas 0 a 05 Elson Rodrigues, Gabriel Carvalho e Paulo Luiz Sumário DETERMINANTE... Exemplo... Exemplo...... Exemplo...... TEOREMA DE LAPLACE... I) COFATOR... Exemplo... II)
Aula 5 - Produto Vetorial
 Aula 5 - Produto Vetorial Antes de iniciar o conceito de produto vetorial, precisamos recordar como se calculam os determinantes. Mas o que é um Determinante? Determinante é uma função matricial que associa
Aula 5 - Produto Vetorial Antes de iniciar o conceito de produto vetorial, precisamos recordar como se calculam os determinantes. Mas o que é um Determinante? Determinante é uma função matricial que associa
Notas para o Curso de Algebra Linear Il Dayse Haime Pastore 20 de fevereiro de 2009
 Notas para o Curso de Álgebra Linear Il Dayse Haime Pastore 20 de fevereiro de 2009 2 Sumário 1 Matrizes e Sistemas Lineares 5 11 Matrizes 6 12 Sistemas Lineares 11 121 Eliminação Gaussiana 12 122 Resolução
Notas para o Curso de Álgebra Linear Il Dayse Haime Pastore 20 de fevereiro de 2009 2 Sumário 1 Matrizes e Sistemas Lineares 5 11 Matrizes 6 12 Sistemas Lineares 11 121 Eliminação Gaussiana 12 122 Resolução
Hewlett-Packard DETERMINANTE. Aulas 01 a 05. Elson Rodrigues, Gabriel Carvalho e Paulo Luiz
 Hewlett-Packard DETERMINANTE Aulas 0 a 05 Elson Rodrigues, Gabriel Carvalho e Paulo Luiz Sumário DETERMINANTE... Exemplo... Exemplo...... Exemplo...... TEOREMA DE LAPLACE... I) COFATOR... Exemplo... II)
Hewlett-Packard DETERMINANTE Aulas 0 a 05 Elson Rodrigues, Gabriel Carvalho e Paulo Luiz Sumário DETERMINANTE... Exemplo... Exemplo...... Exemplo...... TEOREMA DE LAPLACE... I) COFATOR... Exemplo... II)
. (1) Se S é o espaço vetorial gerado pelos vetores 1 e,0,1
 QUESTÕES ANPEC ÁLGEBRA LINEAR QUESTÃO 0 Assinale V (verdadeiro) ou F (falso): (0) Os vetores (,, ) (,,) e (, 0,) formam uma base de,, o espaço vetorial gerado por,, e,, passa pela origem na direção de,,
QUESTÕES ANPEC ÁLGEBRA LINEAR QUESTÃO 0 Assinale V (verdadeiro) ou F (falso): (0) Os vetores (,, ) (,,) e (, 0,) formam uma base de,, o espaço vetorial gerado por,, e,, passa pela origem na direção de,,
Álgebra Linear. Determinantes, Valores e Vectores Próprios. Jorge Orestes Cerdeira Instituto Superior de Agronomia
 Álgebra Linear Determinantes, Valores e Vectores Próprios Jorge Orestes Cerdeira Instituto Superior de Agronomia - 200 - ISA/UTL Álgebra Linear 200/ 2 Conteúdo Determinantes 5 2 Valores e vectores próprios
Álgebra Linear Determinantes, Valores e Vectores Próprios Jorge Orestes Cerdeira Instituto Superior de Agronomia - 200 - ISA/UTL Álgebra Linear 200/ 2 Conteúdo Determinantes 5 2 Valores e vectores próprios
Matriz, Sistema Linear e Determinante
 Matriz, Sistema Linear e Determinante 1.0 Sistema de Equações Lineares Equação linear de n variáveis x 1, x 2,..., x n é uma equação que pode ser expressa na forma a1x1 + a 2 x 2 +... + a n x n = b, onde
Matriz, Sistema Linear e Determinante 1.0 Sistema de Equações Lineares Equação linear de n variáveis x 1, x 2,..., x n é uma equação que pode ser expressa na forma a1x1 + a 2 x 2 +... + a n x n = b, onde
Geometria Analítica. Prof Marcelo Maraschin de Souza
 Geometria Analítica Prof Marcelo Maraschin de Souza Vetor Definido por dois pontos Seja o vetor AB de origem no ponto A(x 1, y 1 ) e extremidade no ponto B(x 2, y 2 ). Qual é a expressão algébrica que
Geometria Analítica Prof Marcelo Maraschin de Souza Vetor Definido por dois pontos Seja o vetor AB de origem no ponto A(x 1, y 1 ) e extremidade no ponto B(x 2, y 2 ). Qual é a expressão algébrica que
Aula 3 Vetores no espaço
 MÓDULO 1 - AULA 3 Aula 3 Vetores no espaço Objetivos Ampliar a noção de vetor para o espaço. Rever as operações com vetores e sua representação em relação a um sistema ortogonal de coordenadas cartesianas.
MÓDULO 1 - AULA 3 Aula 3 Vetores no espaço Objetivos Ampliar a noção de vetor para o espaço. Rever as operações com vetores e sua representação em relação a um sistema ortogonal de coordenadas cartesianas.
Transformações geométricas planas
 9 Transformações geométricas planas Sumário 9.1 Introdução....................... 2 9.2 Transformações no plano............... 2 9.3 Transformações lineares................ 5 9.4 Operações com transformações...........
9 Transformações geométricas planas Sumário 9.1 Introdução....................... 2 9.2 Transformações no plano............... 2 9.3 Transformações lineares................ 5 9.4 Operações com transformações...........
1. Conhecendo-se somente os produtos AB e AC, calcule A = X 2 = 2X. 3. Mostre que se A e B são matrizes que comutam com a matriz M = 1 0
 Lista de exercícios. AL. 1 sem. 2015 Prof. Fabiano Borges da Silva 1 Matrizes Notações: 0 para matriz nula; I para matriz identidade; 1. Conhecendo-se somente os produtos AB e AC calcule A(B + C) B t A
Lista de exercícios. AL. 1 sem. 2015 Prof. Fabiano Borges da Silva 1 Matrizes Notações: 0 para matriz nula; I para matriz identidade; 1. Conhecendo-se somente os produtos AB e AC calcule A(B + C) B t A
1 a Lista de Exercícios MAT 3211 Álgebra Linear Prof. Vyacheslav Futorny
 1 a Lista de Exercícios MAT 3211 Álgebra Linear - 213 - Prof. Vyacheslav Futorny 1 a parte: Resolução de sistemas de equações lineares, matrizes inversíveis 1. Para cada um dos seguintes sistemas de equações
1 a Lista de Exercícios MAT 3211 Álgebra Linear - 213 - Prof. Vyacheslav Futorny 1 a parte: Resolução de sistemas de equações lineares, matrizes inversíveis 1. Para cada um dos seguintes sistemas de equações
(x 1, y 1 ) (x 2, y 2 ) = (x 1 x 2, y 1 y 2 ); e α (x, y) = (x α, y α ), α R.
 INSTITUTO DE MATEMÁTICA E ESTATÍSTICA UNIVERSIDADE DE SÃO PAULO MAT-2457 Álgebra Linear para Engenharia I Terceira Lista de Exercícios - Professor: Equipe da Disciplina EXERCÍCIOS 1. Considere as retas
INSTITUTO DE MATEMÁTICA E ESTATÍSTICA UNIVERSIDADE DE SÃO PAULO MAT-2457 Álgebra Linear para Engenharia I Terceira Lista de Exercícios - Professor: Equipe da Disciplina EXERCÍCIOS 1. Considere as retas
. f3 = 4 e 1 3 e 2. f2 = e 1 e 3, g 1 = e 1 + e 2 + e 3, 2 g 2 = e 1 + e 2,
 INSTITUTO DE MATEMÁTICA E ESTATÍSTICA UNIVERSIDADE DE SÃO PAULO MAT-457 Álgebra Linear para Engenharia I Segunda Lista de Exercícios - Professor: Equipe da Disciplina EXERCÍCIOS 1. Dê a matriz de mudança
INSTITUTO DE MATEMÁTICA E ESTATÍSTICA UNIVERSIDADE DE SÃO PAULO MAT-457 Álgebra Linear para Engenharia I Segunda Lista de Exercícios - Professor: Equipe da Disciplina EXERCÍCIOS 1. Dê a matriz de mudança
Instituto Superior Técnico Departamento de Matemática Última actualização: 18/Nov/2003 ÁLGEBRA LINEAR A
 Instituto Superior Técnico Departamento de Matemática Secção de Álgebra e Análise Última actualização: 18/Nov/2003 ÁLGEBRA LINEAR A REVISÃO DA PARTE III Parte III - (a) Ortogonalidade Conceitos: produto
Instituto Superior Técnico Departamento de Matemática Secção de Álgebra e Análise Última actualização: 18/Nov/2003 ÁLGEBRA LINEAR A REVISÃO DA PARTE III Parte III - (a) Ortogonalidade Conceitos: produto
Álgebra Linear. Professor Alessandro Monteiro. 1º Sábado - Matrizes - 11/03/2017
 º Sábado - Matrizes - //7. Plano e Programa de Ensino. Definição de Matrizes. Exemplos. Definição de Ordem de Uma Matriz. Exemplos. Representação Matriz Genérica m x n 8. Matriz Linha 9. Exemplos. Matriz
º Sábado - Matrizes - //7. Plano e Programa de Ensino. Definição de Matrizes. Exemplos. Definição de Ordem de Uma Matriz. Exemplos. Representação Matriz Genérica m x n 8. Matriz Linha 9. Exemplos. Matriz
Equações da reta no plano
 3 Equações da reta no plano Sumário 3.1 Introdução....................... 2 3.2 Equação paramétrica da reta............. 2 3.3 Equação cartesiana da reta.............. 7 3.4 Equação am ou reduzida da reta..........
3 Equações da reta no plano Sumário 3.1 Introdução....................... 2 3.2 Equação paramétrica da reta............. 2 3.3 Equação cartesiana da reta.............. 7 3.4 Equação am ou reduzida da reta..........
FACULDADE DE ENGENHARIA DA UNIVERSIDADE DO PORTO LEEC EXERCÍCIOS DE ÁLGEBRA
 FACULDADE DE ENGENHARIA DA UNIVERSIDADE DO PORTO LEEC EXERCÍCIOS DE ÁLGEBRA Exercícios vários. Considere o conjunto C =, e a operação binária definida por a b = min(a, b). O conjunto C é, relativamente
FACULDADE DE ENGENHARIA DA UNIVERSIDADE DO PORTO LEEC EXERCÍCIOS DE ÁLGEBRA Exercícios vários. Considere o conjunto C =, e a operação binária definida por a b = min(a, b). O conjunto C é, relativamente
Testes e Sebentas. Exercícios resolvidos de Álgebra Linear (Matrizes e Determinantes)
 Testes e Sebentas Exercícios resolvidos de Álgebra Linear (Matrizes e Determinantes) Índice: 1. Matrizes 1.1. Igualdade de matrizes 3 1.2. Transposta de uma matriz 3 1.3. Multiplicação por um escalar 3
Testes e Sebentas Exercícios resolvidos de Álgebra Linear (Matrizes e Determinantes) Índice: 1. Matrizes 1.1. Igualdade de matrizes 3 1.2. Transposta de uma matriz 3 1.3. Multiplicação por um escalar 3
Coordenadas e vetores no espaço
 13 Coordenadas e vetores no espaço Sumário 13.1 Coordenadas no espaço................ 2 13.2 Distância entre dois pontos do espaço........ 6 13.3 Vetores no espaço................... 10 13.4 Operações
13 Coordenadas e vetores no espaço Sumário 13.1 Coordenadas no espaço................ 2 13.2 Distância entre dois pontos do espaço........ 6 13.3 Vetores no espaço................... 10 13.4 Operações
Álgebra Linear I - Lista 10. Matrizes e Transformações lineares. Respostas
 Álgebra Linear I - Lista 1 Matrizes e Transformações lineares Respostas 1 Sejam A e B matrizes quadradas do mesmo tamanho Dê um exemplo onde (A + B 2 A 2 + 2A B + B 2 Complete: (A + B 2 = A 2 + B 2 +?
Álgebra Linear I - Lista 1 Matrizes e Transformações lineares Respostas 1 Sejam A e B matrizes quadradas do mesmo tamanho Dê um exemplo onde (A + B 2 A 2 + 2A B + B 2 Complete: (A + B 2 = A 2 + B 2 +?
1 a Lista de Exercícios MAT 105 Geometria Analitica
 1 a Lista de Exercícios MAT 105 Geometria Analitica - 2017 1 a parte: Vetores, operações com vetores 1. Demonstre que o segmento que une os pontos médios dos lados não paralelos de um trapézio é paralelo
1 a Lista de Exercícios MAT 105 Geometria Analitica - 2017 1 a parte: Vetores, operações com vetores 1. Demonstre que o segmento que une os pontos médios dos lados não paralelos de um trapézio é paralelo
A Reta no Espaço. Sumário
 16 A Reta no Espaço Sumário 16.1 Introdução....................... 2 16.2 Equações paramétricas da reta no espaço...... 2 16.3 Equação simétrica da reta no espaço........ 8 16.4 Exercícios........................
16 A Reta no Espaço Sumário 16.1 Introdução....................... 2 16.2 Equações paramétricas da reta no espaço...... 2 16.3 Equação simétrica da reta no espaço........ 8 16.4 Exercícios........................
ALGEBRA LINEAR 1 RESUMO E EXERCÍCIOS* P1
 ALGEBRA LINEAR 1 RESUMO E EXERCÍCIOS* P1 *Exercícios de provas anteriores escolhidos para você estar preparado para qualquer questão na prova. Resoluções em VETORES Um vetor é uma lista ordenada de números
ALGEBRA LINEAR 1 RESUMO E EXERCÍCIOS* P1 *Exercícios de provas anteriores escolhidos para você estar preparado para qualquer questão na prova. Resoluções em VETORES Um vetor é uma lista ordenada de números
ficha 1 matrizes e sistemas de equações lineares
 Exercícios de Álgebra Linear ficha matrizes e sistemas de equações lineares Exercícios coligidos por Jorge Almeida e Lina Oliveira Departamento de Matemática, Instituto Superior Técnico 2 o semestre 2/2
Exercícios de Álgebra Linear ficha matrizes e sistemas de equações lineares Exercícios coligidos por Jorge Almeida e Lina Oliveira Departamento de Matemática, Instituto Superior Técnico 2 o semestre 2/2
CVGA Edezio 1. k e v = x2. u, v = u v = x 1 x 2 + y 1 y 2 + z 1 z 2
 CVGA Edezio 1 Cálculo Vetorial e Geometria Analítica Produto de Vetores Produto Escalar (ou Interno) Chama-se produto escalar (ou produto interno usual) de dois vetores x 1 i + y1 j + z1 k e x2 i + y2
CVGA Edezio 1 Cálculo Vetorial e Geometria Analítica Produto de Vetores Produto Escalar (ou Interno) Chama-se produto escalar (ou produto interno usual) de dois vetores x 1 i + y1 j + z1 k e x2 i + y2
Lista 1 com respostas
 Lista 1 com respostas Professora Nataliia Goloshchapova MAT0105-1 semestre de 2019 Exercício 1. Verique se é verdadeira ou falsa cada armação e justique sua resposta: (a) (A, B) (C, D) AB = CD (b) AB =
Lista 1 com respostas Professora Nataliia Goloshchapova MAT0105-1 semestre de 2019 Exercício 1. Verique se é verdadeira ou falsa cada armação e justique sua resposta: (a) (A, B) (C, D) AB = CD (b) AB =
UNIVERSIDADE FEDERAL DO PARÁ CÁLCULO II - PROJETO NEWTON AULA 04. v = x 2 + y 2. v = x1 x 2 + y 1 y 2. v = 0. v = x 2 + y 2 + z 2
 UNIVERSIDADE FEDERAL DO PARÁ CÁLCULO II - PROJETO NEWTON AULA 04 Assunto:Produto escalar, bases canônicas do R 2 e R 3, produto vetorial, produto misto, equação da reta no R 2 Palavras-chaves: Produto
UNIVERSIDADE FEDERAL DO PARÁ CÁLCULO II - PROJETO NEWTON AULA 04 Assunto:Produto escalar, bases canônicas do R 2 e R 3, produto vetorial, produto misto, equação da reta no R 2 Palavras-chaves: Produto
Matrizes e Linearidade
 Matrizes e Linearidade 1. Revisitando Matrizes 1.1. Traço, Simetria, Determinante 1.. Inversa. Sistema de Equações Lineares. Equação Característica.1. Autovalor & Autovetor 4. Polinômios Coprimos 5. Função
Matrizes e Linearidade 1. Revisitando Matrizes 1.1. Traço, Simetria, Determinante 1.. Inversa. Sistema de Equações Lineares. Equação Característica.1. Autovalor & Autovetor 4. Polinômios Coprimos 5. Função
Álgebra Linear e Geometria Anaĺıtica. Matrizes e Sistemas de Equações Lineares
 universidade de aveiro departamento de matemática Álgebra Linear e Geometria Anaĺıtica Agrupamento IV (ECT, EET, EI) Capítulo 1 Matrizes e Sistemas de Equações Lineares Geometria anaĺıtica em R 3 [1 01]
universidade de aveiro departamento de matemática Álgebra Linear e Geometria Anaĺıtica Agrupamento IV (ECT, EET, EI) Capítulo 1 Matrizes e Sistemas de Equações Lineares Geometria anaĺıtica em R 3 [1 01]
Aula 3 A Reta e a Dependência Linear
 MÓDULO 1 - AULA 3 Aula 3 A Reta e a Dependência Linear Objetivos Determinar a equação paramétrica de uma reta no plano. Compreender o paralelismo entre retas e vetores. Entender a noção de dependência
MÓDULO 1 - AULA 3 Aula 3 A Reta e a Dependência Linear Objetivos Determinar a equação paramétrica de uma reta no plano. Compreender o paralelismo entre retas e vetores. Entender a noção de dependência
2. Determine a ordem das matrizes A, B, C, D e E, sabendo-se que AB T tem ordem 5 3, (C T +D)B tem ordem 4 6 e E T C tem ordem 5 4.
 Universidade Federal de Viçosa Centro de Ciências Exatas e Tecnológicas Departamento de Matemática 1 a Lista - MAT 17 - Introdução à Álgebra Linear 2016/II 1 Considere as matrizes A, B, C, D e E com respectivas
Universidade Federal de Viçosa Centro de Ciências Exatas e Tecnológicas Departamento de Matemática 1 a Lista - MAT 17 - Introdução à Álgebra Linear 2016/II 1 Considere as matrizes A, B, C, D e E com respectivas
Aulas práticas de Álgebra Linear
 Ficha Matrizes e sistemas de equações lineares Aulas práticas de Álgebra Linear Mestrado Integrado em Engenharia Eletrotécnica e de Computadores o semestre 6/7 Jorge Almeida e Lina Oliveira Departamento
Ficha Matrizes e sistemas de equações lineares Aulas práticas de Álgebra Linear Mestrado Integrado em Engenharia Eletrotécnica e de Computadores o semestre 6/7 Jorge Almeida e Lina Oliveira Departamento
MATEMÁTICA MÓDULO 11 DETERMINANTES. Professor Matheus Secco
 MATEMÁTICA Professor Matheus Secco MÓDULO 11 DETERMINANTES INTRODUÇÃO Neste módulo, não daremos a definição padrão de determinantes via somatório envolvendo sinais de permutações, pois não há necessidade
MATEMÁTICA Professor Matheus Secco MÓDULO 11 DETERMINANTES INTRODUÇÃO Neste módulo, não daremos a definição padrão de determinantes via somatório envolvendo sinais de permutações, pois não há necessidade
Lista de Álgebra Linear Aplicada
 Lista de Álgebra Linear Aplicada Matrizes - Vetores - Retas e Planos 3 de setembro de 203 Professor: Aldo Bazán Universidade Federal Fluminense Matrizes. Seja A M 2 2 (R) definida como 0 0 0 3 0 0 0 2
Lista de Álgebra Linear Aplicada Matrizes - Vetores - Retas e Planos 3 de setembro de 203 Professor: Aldo Bazán Universidade Federal Fluminense Matrizes. Seja A M 2 2 (R) definida como 0 0 0 3 0 0 0 2
MAT Álgebra Linear para Engenharia II - Poli 2 ō semestre de ā Lista de Exercícios
 MAT 2458 - Álgebra Linear para Engenharia II - Poli 2 ō semestre de 2014 1 ā Lista de Exercícios 1. Verifique se V = {(x, y) x, y R} é um espaço vetorial sobre R com as operações de adição e de multiplicação
MAT 2458 - Álgebra Linear para Engenharia II - Poli 2 ō semestre de 2014 1 ā Lista de Exercícios 1. Verifique se V = {(x, y) x, y R} é um espaço vetorial sobre R com as operações de adição e de multiplicação
Espaços Euclidianos. Espaços R n. O conjunto R n é definido como o conjunto de todas as n-uplas ordenadas de números reais:
 Espaços Euclidianos Espaços R n O conjunto R n é definido como o conjunto de todas as n-uplas ordenadas de números reais: R n = {(x 1,..., x n ) : x 1,..., x n R}. R 1 é simplesmente o conjunto R dos números
Espaços Euclidianos Espaços R n O conjunto R n é definido como o conjunto de todas as n-uplas ordenadas de números reais: R n = {(x 1,..., x n ) : x 1,..., x n R}. R 1 é simplesmente o conjunto R dos números
Álgebra Linear AL. Luiza Amalia Pinto Cantão. Depto. de Engenharia Ambiental Universidade Estadual Paulista UNESP
 Álgebra Linear AL Luiza Amalia Pinto Cantão Depto de Engenharia Ambiental Universidade Estadual Paulista UNESP luiza@sorocabaunespbr Matrizes Inversas 1 Matriz Inversa e Propriedades 2 Cálculo da matriz
Álgebra Linear AL Luiza Amalia Pinto Cantão Depto de Engenharia Ambiental Universidade Estadual Paulista UNESP luiza@sorocabaunespbr Matrizes Inversas 1 Matriz Inversa e Propriedades 2 Cálculo da matriz
é encontrado no cruzamento da linha i com a coluna j, ou seja, o primeiro índice se refere à linha e o segundo à coluna.
 Ministério da Educação Secretaria de Educação Profissional e Tecnológica Instituto Federal De Santa Catarina Campus São José Professora: ELENIRA OLIVEIRA VILELA COMPONENTE CURRICULAR: ALG ÁLG. LINEAR MATRIZES
Ministério da Educação Secretaria de Educação Profissional e Tecnológica Instituto Federal De Santa Catarina Campus São José Professora: ELENIRA OLIVEIRA VILELA COMPONENTE CURRICULAR: ALG ÁLG. LINEAR MATRIZES
Álgebra Linear Semana 04
 Álgebra Linear Semana 04 Diego Marcon 17 de Abril de 2017 Conteúdo 1 Produto de matrizes 1 11 Exemplos 2 12 Uma interpretação para resolução de sistemas lineares 3 2 Matriz transposta 4 3 Matriz inversa
Álgebra Linear Semana 04 Diego Marcon 17 de Abril de 2017 Conteúdo 1 Produto de matrizes 1 11 Exemplos 2 12 Uma interpretação para resolução de sistemas lineares 3 2 Matriz transposta 4 3 Matriz inversa
Lista de exercícios 7 Independência Linear.
 Universidade Federal do Paraná semestre 6. Algebra Linear Olivier Brahic Lista de exercícios 7 Independência Linear. Exercício : Determine se os seguintes vetores são linearmente independentes em R : (
Universidade Federal do Paraná semestre 6. Algebra Linear Olivier Brahic Lista de exercícios 7 Independência Linear. Exercício : Determine se os seguintes vetores são linearmente independentes em R : (
Hewlett-Packard DETERMINANTE. Aulas 01 a 04. Elson Rodrigues, Gabriel Carvalho e Paulo Luiz
 Hewlett-Packard DETERMINANTE Aulas 0 a 04 Elson Rodrigues, Gabriel Carvalho e Paulo Luiz Ano: 206 Sumário DETERMINANTE... Exemplo... Exemplo 2... EXERCÍCIOS FUNDAMENTAIS... Exemplo 3... EXERCÍCIOS FUNDAMENTAIS...
Hewlett-Packard DETERMINANTE Aulas 0 a 04 Elson Rodrigues, Gabriel Carvalho e Paulo Luiz Ano: 206 Sumário DETERMINANTE... Exemplo... Exemplo 2... EXERCÍCIOS FUNDAMENTAIS... Exemplo 3... EXERCÍCIOS FUNDAMENTAIS...
ALGA - Eng.Civil e Eng. Topográ ca - ISE /
 ALGA - Eng.Civil e Eng. Topográ ca - ISE - 0/0 0. (a) Calcule o sinal das seguintes permutações (i) (; ; ; ; ) (ii) (; ; ; ; ; ) (b) Use os resultados da alínea (a) para calcular, usando a de nição, os
ALGA - Eng.Civil e Eng. Topográ ca - ISE - 0/0 0. (a) Calcule o sinal das seguintes permutações (i) (; ; ; ; ) (ii) (; ; ; ; ; ) (b) Use os resultados da alínea (a) para calcular, usando a de nição, os
Objetivos. em termos de produtos internos de vetores.
 Aula 5 Produto interno - Aplicações MÓDULO 1 - AULA 5 Objetivos Calcular áreas de paralelogramos e triângulos. Calcular a distância de um ponto a uma reta e entre duas retas. Determinar as bissetrizes
Aula 5 Produto interno - Aplicações MÓDULO 1 - AULA 5 Objetivos Calcular áreas de paralelogramos e triângulos. Calcular a distância de um ponto a uma reta e entre duas retas. Determinar as bissetrizes
MATRIZES. Álgebra Linear e Geometria Analítica Prof. Aline Paliga
 MATRIZES Álgebra Linear e Geometria Analítica Prof. Aline Paliga INTRODUÇÃO Definição: chama-se matriz de ordem m por n a um quadro de m xn elementos dispostos em m linhas e n colunas. a a a a a a a a
MATRIZES Álgebra Linear e Geometria Analítica Prof. Aline Paliga INTRODUÇÃO Definição: chama-se matriz de ordem m por n a um quadro de m xn elementos dispostos em m linhas e n colunas. a a a a a a a a
Econometria. Operações básicas de vetores. Operações básicas de vetores. Operações básicas de vetores. Independência de vetores
 Operações básicas de vetores Econometria Adição Suponha dois vetores x e y com n componentes cada: 1. Alguns tópicos importantes de Álgebra Linear Operações básicas de vetores Multiplicação escalar x é
Operações básicas de vetores Econometria Adição Suponha dois vetores x e y com n componentes cada: 1. Alguns tópicos importantes de Álgebra Linear Operações básicas de vetores Multiplicação escalar x é
Seja f um endomorfismo de um espaço vectorial E de dimensão finita.
 6. Valores e Vectores Próprios 6.1 Definição, exemplos e propriedades Definição Seja f um endomorfismo de um espaço vectorial E, com E de dimensão finita, e seja B uma base arbitrária de E. Chamamos polinómio
6. Valores e Vectores Próprios 6.1 Definição, exemplos e propriedades Definição Seja f um endomorfismo de um espaço vectorial E, com E de dimensão finita, e seja B uma base arbitrária de E. Chamamos polinómio
4-Operações de Matrizes
 4-Operações de Matrizes Laura Goulart UESB 30 de Outubro de 2018 Laura Goulart (UESB) 4-Operações de Matrizes 30 de Outubro de 2018 1 / 16 4.1 - Adição de matrizes Dadas as matrizes A = (a ij ) e B = (b
4-Operações de Matrizes Laura Goulart UESB 30 de Outubro de 2018 Laura Goulart (UESB) 4-Operações de Matrizes 30 de Outubro de 2018 1 / 16 4.1 - Adição de matrizes Dadas as matrizes A = (a ij ) e B = (b
São tabelas de elementos dispostos ordenadamente em linhas e colunas.
 EMENTA (RESUMO) Matrizes Matrizes, determinantes e suas propriedades, Multiplicação de matrizes, Operações com matrizes, Matrizes inversíveis. Sistemas de Equações Lineares Sistemas equações lineares,
EMENTA (RESUMO) Matrizes Matrizes, determinantes e suas propriedades, Multiplicação de matrizes, Operações com matrizes, Matrizes inversíveis. Sistemas de Equações Lineares Sistemas equações lineares,
Resolução do efólio A
 Resolução do efólio A Álgebra Linear I Código: 21002 I. Questões de escolha múltipla. Em cada questão de escolha múltipla apenas uma das armações a), b), c), d) é verdadeira. Indique-a marcando ˆ no quadrado
Resolução do efólio A Álgebra Linear I Código: 21002 I. Questões de escolha múltipla. Em cada questão de escolha múltipla apenas uma das armações a), b), c), d) é verdadeira. Indique-a marcando ˆ no quadrado
