Nota de aula 8 - Estado Plano de Tensões - Resistência dos Materiais II
|
|
|
- Renata Mendes Amaral
- 6 Há anos
- Visualizações:
Transcrição
1 Nota de aula 8 - Estado Plano de Tensões - Resistência dos Materiais II Flávia Bastos (retirado da apostila do Prof. Elson Toledo) MAC - Faculdade de Engenharia - UFJF o. semestre de 011 Flávia Bastos RESMAT II 1/18
2 Caso particular do problema 3D Informações sobre este documento: Estes slides servem para auxiliar no desenvolvimento expositivo durante as aulas de resistência dos materiais II ministradas pela professora Flávia Bastos e são baseados na apostila do Prof. Elson Toledo. Flávia Bastos RESMAT II /18
3 Caso particular do problema 3D Estado Plano de Tensões Figura: Caso particular do problema 3D Flávia Bastos RESMAT II 3/18
4 Expressões Gerais Caso particular do problema 3D ρ n = Ñ Vetor tensão total σ n = σ ρ n Ñ Tensão normal τ n = ρ n σ n Tensão tangencial No caso de problemas de estado plano de tensão, temos que: [ ] σxx τ = xy (1) σ τ xy σ yy Ñ = [ l x l y ] = [ cosα senα ] α ângulo que Ñ faz com o eixo x. () Flávia Bastos RESMAT II 4/18
5 Expressões Gerais Caso particular do problema 3D Temos então: { ρnx ρ ny } [ σxx τ = xy τ xy σ yy ] { cosα senα } (3) A tensão normal então fica: { ρnx = σ xx cosα + τ xy senα ρ ny = τ xy cosα + σ yy senα (4) σ n = ρ nx cosα + ρ ny senα = (σ xx cosα + τ xy senα)cosα + (τ xy cosα + σ yy senα)senα = σ xx cos α + τ xy senαcosα + σ yy sen α (5) Flávia Bastos RESMAT II 5/18
6 Expressões Gerais Caso particular do problema 3D Como: Chegamos a: { cos α = 1+cosα sen α = 1 cosα (6) σ n = σ xx + σ yy + σ xx σ yy cosα + τ xy senα (7) Flávia Bastos RESMAT II 6/18
7 Expressões Gerais Caso particular do problema 3D A tensão tangencial fica: τ n = ρ nx + ρ ny (ρ nx cosα + ρ ny senα) (8) τn = ρ nx(1 cos α) + ρ ny(1 sen α) ρ nx ρ ny senαcosα = ρ nxsen α + ρ nycos α ρ nx ρ ny senαcosα = (ρ ny cosα ρ nx senα) (9) τ n = ρ ny cosα ρ nx senα (10) Flávia Bastos RESMAT II 7/18
8 Expressões Gerais Caso particular do problema 3D Substituindo as expressões de ρ nx e ρ ny nesta fórmula: τ n = (τ xy cosα + σ yy senα)cosα (σ xx cosα + τ xy senα)senα = τ xy cos α + σ yy senαcosα (σ xx cosαsenα + τ xy sen α) (11) O que nos leva a: τ n = σ yy σ xx senα + τ xy cosα (1) Flávia Bastos RESMAT II 8/18
9 Caso particular do problema 3D Tensões Normais Principais A determinação das tensões principais pode ser feita a partir da equação característica para este caso. Sendo: [ ] σxx τ σ = xy (13) τ xy σ yy A equação característica que permite calcular as tensões principais escreve-se: ( ) det σ l Ĩ = 0 (14) σ onde σ l é a tensão principal e Ĩ [ é o tensor identidade de ] 1 0 segunda ordem Ĩ = 0 1 Flávia Bastos RESMAT II 9/18
10 Caso particular do problema 3D Tensões Normais Principais Ficamos então com: σ xx σ l τ xy τ xy σ yy σ l = 0 (15) (σ xx σ l )(σ yy σ l ) τ xy = 0 (16) cujas raizes são: σ ξ = σxx+σyy + σ l (σ xx + σ yy )σ l + σ xx σ yy τ xy = 0 (17) ( ) σxx σ yy + τ xy σ η = σxx+σyy ( σxx σ yy ) + τ xy Flávia Bastos RESMAT II 10/18
11 Caso particular do problema 3D Tensões Principais como valores extremos De: σ n = σ xx + σ yy + σ xx σ yy cosα + τ xy senα (18) dσ n dα = 0 σ xx σ yy senα + τ xy cosα = 0 (19) Que resulta em: tgα = que possui duas soluções α 0 e α 0 + π. τ xy σ xx σ yy (0) Flávia Bastos RESMAT II 11/18
12 Caso particular do problema 3D Tensões Principais como valores extremos Para a determinação do valor de σ n no plano com α dado pela solução da equação trigonométrica acima construimos o triângulo***: senα = cosα = τ xy (σ xx σ yy ) + 4τ xy (σ xx σ yy ) (σ xx σ yy ) + 4τxy (1) () Flávia Bastos RESMAT II 1/18
13 Caso particular do problema 3D Tensões Principais como valores extremos Substituindo na expressão de σ n resulta em: σ ξ,η = σ xx + σ yy ± (σxx σ yy ) + τ xy (3) O que mostra que as tensões principais são os valores extremos (máximo e mínimo) entre todas as tensões normais atuantes no ponto. Flávia Bastos RESMAT II 13/18
14 Caso particular do problema 3D Tensões Tangenciais Máximas A determinação dos valores extremos da tensão tangencial em um ponto é obtido através de: τ n = σ xx σ yy senα + τ xy cosα (4) dτ n dα = σ xx σ yy cosα τ xy senα = 0 (5) que resulta em: que possui duas soluções α 0 e α 0 + π. tgα = σ xx σ yy τ xy (6) Flávia Bastos RESMAT II 14/18
15 Caso particular do problema 3D Tensões Tangenciais Máximas A determinação dos extremos é feita a partir do triângulo*** (mnemônico): cosα = senα = τ xy (σ xx σ yy ) + 4τ xy (σ xx σ yy ) (σ xx σ yy ) + 4τxy (7) (8) Flávia Bastos RESMAT II 15/18
16 Caso particular do problema 3D Tensões Tangenciais Máximas que substituídos na expressão de τ n resulta: τ nmax/min = ± (σxx σ yy ) + τ xy (9) Pode-se constatar, subtraindo σ ξ de σ η, obtidos na página anterior, que: (σxx σ yy σ ξ σ η = De onde concluímos que: ) + τ xy (30) τ max = τ min = σ ξ σ η (31) Flávia Bastos RESMAT II 16/18
17 Caso particular do problema 3D Posição relativa entre as direções de σ nmax e τ max O ângulo α 0 onde as tensões normais são máximas é dado por: tg(α 0 ) = τ xy σ xx σ yy (3) E o ângulo α 0 onde as tensões tangenciais são máximas é dado por: tg(α 0 ) = σ xx σ yy τ xy (33) Multiplicando-se uma expressão pela outra, obtém-se: tg(α 0 )tg(α 0 ) = 1 (34) Flávia Bastos RESMAT II 17/18
18 Caso particular do problema 3D Posição relativa entre as direções de σ nmax e τ max Logo α 0 e α 0 diferem de π isto é: ou α 0 = α 0 + π α 0 = α 0 + π 4 (35) (36) Logo concluimos que os planos nos quais ocorrem as tensões normais extremas formam um ângulo de 45 o com os planos nos quais as tensões tangenciais são máximas. Flávia Bastos RESMAT II 18/18
19 Nota de aula 9 - Estado Plano de Tensões - Resistência dos Materiais II Flávia Bastos (retirado da apostila do Prof. Elson Toledo) MAC - Faculdade de Engenharia - UFJF o. semestre de 011 Flávia Bastos RESMAT II 1/16
20 Informações sobre este documento: Estes slides servem para auxiliar no desenvolvimento expositivo durante as aulas de resistência dos materiais II ministradas pela professora Flávia Bastos e são baseados na apostila do Prof. Elson Toledo. Flávia Bastos RESMAT II /16
21 O par (σ n, τ n ) das tensões normal e tangencial em um plano qualquer, num estado plano de tensões gera uma figura no plano de coordenadas σ, τ que é conhecida como círculo de Mohr. Temos que σ n e τ n podem ser determinados por: { σn = σxx+σyy + σxx σyy cosα + τ xy senα τ n = σxx σyy senα + τ xy cosα Chamando σ m = σxx+σyy temos: { σn σ m = σxx σyy cosα + τ xy senα τ n = σxx σyy senα + τ xy cosα (1) () Flávia Bastos RESMAT II 3/16
22 Elevando cada um dos termos das igualdades anteriores ao quadrado e somando-os obtém-se: ( (σ n σ m ) + τn σxx σ yy = Chamando σ n = σ; τ n = τ e R = chegamos a: ) + τ xy (3) ( ) σxx σ yy + τ xy, (σ σ m ) + τ = R (4) que é a equação de uma circunferência no plano (σ, τ) com centro sobre o eixo σ no ponto σ = σ m = σxx+σyy e cujo raio é o valor de R acima descrito. Flávia Bastos RESMAT II 4/16
23 M -> Ponto que representa as tensões em torno de P na direção α. Da figura constatamos novamente que a máxima tensão tangencial vale: τ max = R = σ ξ σ η (5) Flávia Bastos RESMAT II 5/16
24 Expressão do círculo de Mohr a partir das tensões principais Considerando como ponto de partida as expressões de σ n e τ n obtidas em função de σ 1 e σ 3 temos: { σ n = σ ξ+σ η + σ ξ σ η cosθ τ n = σ ξ σ η senθ (6) A figura ao lado esclarece o significado dessas expressões. Estas expressões são obtidas das expressões anteriormente vistas para σ n e τ n nas quais fez-se σ xx = σ ξ, σ yy = σ η, τ x,y = 0 e usamos θ no lugar de α. Flávia Bastos RESMAT II 6/16
25 Expressão do círculo de Mohr a partir das tensões principais Chamando σ m = σ ξ+σ η, σ n = σ, τ n = τ e elevando ambas as expressões ao quadrado e somando-as resulta em: ( ) (σ σ m ) + τ σξ σ η = (7) ou ( σ σ ) ξ + σ η + τ = ( ) σξ σ η (8) que descreve o mesmo círculo desenvolvido anteriormente já que: σ xx + σ yy = σ ξ + σ η ( ) σ ξ σ η σxx σ = yy (9) + τ xy = R Flávia Bastos RESMAT II 7/16
26 Casos Particulares i) Estado de tração simples Todas as tensões normais em torno do ponto (em qualquer direção) são de tração. Neste caso: τ max = σ ξ já que σ η = 0! Flávia Bastos RESMAT II 8/16
27 Casos Particulares ii) Estado de compressão simples Todas as tensões normais em torno do ponto (em qualquer direção) são de compressão. Neste caso: τ max = ση já que σ ξ = 0! Flávia Bastos RESMAT II 9/16
28 Casos Particulares iii) Estado de cisalhamento simples Todas as tensões principais são iguais e de sinal contrário. τ max = σ η = σ ξ. Flávia Bastos RESMAT II 10/16
29 Casos Particulares iv) Estado de tensão uniforme ou hidrostático Neste caso σ ξ = σ η = σ e τ = τ max = 0. Flávia Bastos RESMAT II 11/16
30 Decomposição do tensor de tensão Dado um tensor de tensão σ, é possivel decompô-lo do seguinte modo: = σ h + σ σ D onde σ h Tensor de tensão hidrostático; σ Tensor de tensão desviador. D (10) Definindo-se σ como um tensor tal que trσ = 0 e, como já visto (em qualquer D sistema de eixos): D p 0 0 σ h = 0 p 0 (11) 0 0 p Flávia Bastos RESMAT II 1/16
31 Decomposição do tensor de tensão - Determinação das componentes σ h e σ : Se escolhemos as direções principais de D σ para sua descrição temos: σ = 0 σ 0 (1) σ 0 0 σ 3 Logo podemos escrever: = σ σ σ σ 3 = p σ 1 p σ p σ 3 p (13) Flávia Bastos RESMAT II 13/16
32 Decomposição do tensor de tensão Verificação: pela invariância da soma da diagonal principal do tensor de tensão temos que: σ 1 + σ + σ 3 = 3p + (σ 1 p) + (σ p) + (σ 3 p) (14) Escolhendo para σ tensor com traço nulo (soma da diagonal principal), temos que: D e que σ 1 + σ + σ 3 = 3p (15) p = σ 1 + σ + σ 3 3 (16) Flávia Bastos RESMAT II 14/16
33 Decomposição do tensor de tensão Ficamos com (para qualquer sistema de eixos!): p 0 0 σ h = 0 p 0 (17) 0 0 p e σ = σ h (18) D σ Obs: A parcela σ h é responsável pela variação de volume e a parcela σ D, chamada de tensor desviador, é responsável pela mudança de forma como se verá no estudo das deformações. Flávia Bastos RESMAT II 15/16
34 Decomposição do tensor de tensão Concluindo, podemos afirmar que, se = σ então: σ h = σ xx + σ yy + σ zz σ xx τ xy τ xz τ yx σ yy τ yz τ zx τ zy σ zz, (19) e: σ D = σ xx p τ xy τ xz τ yx σ yy p τ yz τ zx τ zy σ zz p com p = σ xx + σ yy + σ zz 3 (0) Flávia Bastos RESMAT II 16/16
Nota de aula 9 - Estado Plano de Tensões - Resistência dos Materiais II
 Nota de aula 9 - Estado Plano de Tensões - Resistência dos Materiais II Flávia Bastos (retirado da apostila do Prof. Elson Toledo) MAC - Faculdade de Engenharia - UFJF o. semestre de 010 Flávia Bastos
Nota de aula 9 - Estado Plano de Tensões - Resistência dos Materiais II Flávia Bastos (retirado da apostila do Prof. Elson Toledo) MAC - Faculdade de Engenharia - UFJF o. semestre de 010 Flávia Bastos
Nota de aula 7 - Estado Triaxial de Tensões - Resistência dos Materiais II
 Nota de aula 7 - Estado Triaxial de Tensões - Resistência dos Materiais II Flávia Bastos (retirado da apostila do Prof. Elson Toledo) MAC - Faculdade de Engenharia - UFJF o. semestre de 010 Flávia Bastos
Nota de aula 7 - Estado Triaxial de Tensões - Resistência dos Materiais II Flávia Bastos (retirado da apostila do Prof. Elson Toledo) MAC - Faculdade de Engenharia - UFJF o. semestre de 010 Flávia Bastos
Nota de aula 5 - Estado Triaxial de Tensões - Resistência dos Materiais II
 Estado Triaxial de Tensões Nota de aula 5 - Estado Triaxial de Tensões - Resistência dos Materiais II Flávia Bastos (retirado da apostila do Prof. Elson Toledo) MAC - Faculdade de Engenharia - UFJF o.
Estado Triaxial de Tensões Nota de aula 5 - Estado Triaxial de Tensões - Resistência dos Materiais II Flávia Bastos (retirado da apostila do Prof. Elson Toledo) MAC - Faculdade de Engenharia - UFJF o.
Nota de aula 10 - Estado Triaxial de Deformações - Resistência dos Materiais II
 Nota de aula 10 - Estado Triaxial de Deformações - Resistência dos Materiais II Flávia Bastos (retirado da apostila do Prof. Elson Toledo) MAC - Faculdade de Engenharia - UFJF 2o. semestre de 2011 Flávia
Nota de aula 10 - Estado Triaxial de Deformações - Resistência dos Materiais II Flávia Bastos (retirado da apostila do Prof. Elson Toledo) MAC - Faculdade de Engenharia - UFJF 2o. semestre de 2011 Flávia
Nota de aula 13 - Estudo da Energia de Deformação - Resistência dos Materiais II
 Nota de aula 13 - Estudo da Energia de Deformação - Resistência dos Materiais II Flávia Bastos (retirado da apostila do Prof. Elson Toledo) MAC - Faculdade de Engenharia - UFJF 2o. semestre de 21 Flávia
Nota de aula 13 - Estudo da Energia de Deformação - Resistência dos Materiais II Flávia Bastos (retirado da apostila do Prof. Elson Toledo) MAC - Faculdade de Engenharia - UFJF 2o. semestre de 21 Flávia
Nota de aula 12 - Lei de Hooke Generalizada - Resistência dos Materiais II
 Nota de aula 12 - Lei de Hooke Generalizada - Resistência dos Materiais II Flávia Bastos (retirado da apostila do Prof. lson Toledo) MAC - Faculdade de ngenharia - UFJF 2o. semestre de 2010 Flávia Bastos
Nota de aula 12 - Lei de Hooke Generalizada - Resistência dos Materiais II Flávia Bastos (retirado da apostila do Prof. lson Toledo) MAC - Faculdade de ngenharia - UFJF 2o. semestre de 2010 Flávia Bastos
UNIVERSIDADE DO ESTADO DE MATO GROSSO CAMPUS DE SINOP FACULDADE DE CIÊNCIAS EXATAS E TECNOLÓGIAS CURSO DE ENGENHARIA CIVIL MECÂNICA DOS SÓLIDOS II
 UNIVERSIDADE DO ESTADO DE MATO GROSSO CAMPUS DE SINOP FACULDADE DE CIÊNCIAS EXATAS E TECNOLÓGIAS CURSO DE ENGENHARIA CIVIL MECÂNICA DOS SÓLIDOS II Aula 01 Teoria das Tensões Eng. Civil Augusto Romanini
UNIVERSIDADE DO ESTADO DE MATO GROSSO CAMPUS DE SINOP FACULDADE DE CIÊNCIAS EXATAS E TECNOLÓGIAS CURSO DE ENGENHARIA CIVIL MECÂNICA DOS SÓLIDOS II Aula 01 Teoria das Tensões Eng. Civil Augusto Romanini
UNIVERSIDADE DO ESTADO DE MATO GROSSO CAMPUS DE SINOP FACULDADE DE CIÊNCIAS EXATAS E TECNOLÓGIAS CURSO DE ENGENHARIA CIVIL MECÂNICA DOS SÓLIDOS II
 UNIVERSIDADE DO ESTADO DE MATO GROSSO CAMPUS DE SINOP FACULDADE DE CIÊNCIAS EXATAS E TECNOLÓGIAS CURSO DE ENGENHARIA CIVIL MECÂNICA DOS SÓLIDOS II Aula 01 Teoria das Tensões Eng. Civil Augusto Romanini
UNIVERSIDADE DO ESTADO DE MATO GROSSO CAMPUS DE SINOP FACULDADE DE CIÊNCIAS EXATAS E TECNOLÓGIAS CURSO DE ENGENHARIA CIVIL MECÂNICA DOS SÓLIDOS II Aula 01 Teoria das Tensões Eng. Civil Augusto Romanini
Resistência dos. Materiais. Capítulo 2. - Elasticidade Linear 2
 Resistência dos Materiais - Elasticidade Linear Acetatos baseados nos livros: - Mechanics of Materials - Beer & Jonhson - Mecânica e Resistência dos Materiais V. Dias da Silva Índice Carregamento Genérico:
Resistência dos Materiais - Elasticidade Linear Acetatos baseados nos livros: - Mechanics of Materials - Beer & Jonhson - Mecânica e Resistência dos Materiais V. Dias da Silva Índice Carregamento Genérico:
Nota de aula 1 - Teoria da Flexão Oblíqua - Resistência dos Materiais II
 Nota de aula 1 - Teoria da Flexão Oblíqua - Resistência dos Materiais II Flávia Bastos (retirado da apostila do Prof. Elson Toledo) MAC - Faculdade de Engenharia - UFJF 2o. semestre de 2010 Flávia Bastos
Nota de aula 1 - Teoria da Flexão Oblíqua - Resistência dos Materiais II Flávia Bastos (retirado da apostila do Prof. Elson Toledo) MAC - Faculdade de Engenharia - UFJF 2o. semestre de 2010 Flávia Bastos
Figura 9.1: Corpo que pode ser simplificado pelo estado plano de tensões (a), estado de tensões no interior do corpo (b).
 9 ESTADO PLANO DE TENSÕES E DEFORMAÇÕES As tensões e deformações em um ponto, no interior de um corpo no espaço tridimensional referenciado por um sistema cartesiano de coordenadas, consistem de três componentes
9 ESTADO PLANO DE TENSÕES E DEFORMAÇÕES As tensões e deformações em um ponto, no interior de um corpo no espaço tridimensional referenciado por um sistema cartesiano de coordenadas, consistem de três componentes
Nota de aula 15 - Flambagem
 Nota de aula 15 - Flambagem Flávia Bastos (retirado da apostila do rof. Elson Toledo) MAC - Faculdade de Engenharia - UFJF 1o. semestre de 2011 Flávia Bastos RESMAT II 1/22 Informações sobre este documento:
Nota de aula 15 - Flambagem Flávia Bastos (retirado da apostila do rof. Elson Toledo) MAC - Faculdade de Engenharia - UFJF 1o. semestre de 2011 Flávia Bastos RESMAT II 1/22 Informações sobre este documento:
Resistência dos Materiais I
 Resistência dos Materiais I Luciano Pessanha Moreira, D.Sc. Professor Associado Departamento de Engenharia Mecânica Escola de Engenharia Metalúrgica Industrial de Volta Redonda Universidade Federal Fluminense
Resistência dos Materiais I Luciano Pessanha Moreira, D.Sc. Professor Associado Departamento de Engenharia Mecânica Escola de Engenharia Metalúrgica Industrial de Volta Redonda Universidade Federal Fluminense
Resistência dos Materiais 2003/2004 Curso de Gestão e Engenharia Industrial
 1/1 Resistência dos Materiais 3/4 Curso de Gestão e Engenharia Industrial 4ª Aula Duração - Horas Data - de Outubro de 3 Sumário: Mudança de Eixos de Referência. Tensões Principais e Direcções Principais.
1/1 Resistência dos Materiais 3/4 Curso de Gestão e Engenharia Industrial 4ª Aula Duração - Horas Data - de Outubro de 3 Sumário: Mudança de Eixos de Referência. Tensões Principais e Direcções Principais.
Estado triplo de tensão
 Estado triplo de tensão Tensões em um ponto Seja um ponto qualquer, pertencente a um corpo em equilíbrio, submetido às tensões representadas na figura. Com esta consideração, a força resultante no plano
Estado triplo de tensão Tensões em um ponto Seja um ponto qualquer, pertencente a um corpo em equilíbrio, submetido às tensões representadas na figura. Com esta consideração, a força resultante no plano
Sumário e Objectivos. 2007/2008 Lúcia M.J.S.Dinis. Mecânica dos Sólidos 2ªAula
 Sumário e Objectivos Sumário: Equações de Equilíbrio de Forças e Momentos. Mudança de Eixos de Referência. Tensões Principais e Direcções Principais. Invariantes das Tensões. Tensor Hidrostático ou Isotrópico.
Sumário e Objectivos Sumário: Equações de Equilíbrio de Forças e Momentos. Mudança de Eixos de Referência. Tensões Principais e Direcções Principais. Invariantes das Tensões. Tensor Hidrostático ou Isotrópico.
Torção de uma Barra Prismática
 Torção de uma Barra Prismática 1 Torção de uma Barra Prismática Torção Uniforme ou de Saint Venant; Aplicação do método semi-inverso. 2 Figura 1. Barra prismática genérica. Barra submetida a momentos de
Torção de uma Barra Prismática 1 Torção de uma Barra Prismática Torção Uniforme ou de Saint Venant; Aplicação do método semi-inverso. 2 Figura 1. Barra prismática genérica. Barra submetida a momentos de
Capítulo 12. Ângulo entre duas retas no espaço. Definição 1. O ângulo (r1, r2 ) entre duas retas r1 e r2 é assim definido:
 Capítulo 1 1. Ângulo entre duas retas no espaço Definição 1 O ângulo (r1, r ) entre duas retas r1 e r é assim definido: (r1, r ) 0o se r1 e r são coincidentes, se as retas são concorrentes, isto é, r1
Capítulo 1 1. Ângulo entre duas retas no espaço Definição 1 O ângulo (r1, r ) entre duas retas r1 e r é assim definido: (r1, r ) 0o se r1 e r são coincidentes, se as retas são concorrentes, isto é, r1
1. Inverta a relação tensão deformação para materiais elásticos, lineares e isotrópicos para obter a relação em termos de deformação.
 Mecânica dos Sólidos I Lista de xercícios III Tensões, Deformações e Relações Constitutivas.. Inverta a relação tensão deformação para materiais elásticos, lineares e isotrópicos para obter a relação em
Mecânica dos Sólidos I Lista de xercícios III Tensões, Deformações e Relações Constitutivas.. Inverta a relação tensão deformação para materiais elásticos, lineares e isotrópicos para obter a relação em
Estados de Tensão e Critérios de ruptura
 Estados de Tensão e Critérios de ruptura GEOTECNIA II SLIDES 09 / AULAS 17 e 18 Prof. MSc. Douglas M. A. Bittencourt prof.douglas.pucgo@gmail.com Tópicos abordados Coeficiente de empuxo em repouso Tensões
Estados de Tensão e Critérios de ruptura GEOTECNIA II SLIDES 09 / AULAS 17 e 18 Prof. MSc. Douglas M. A. Bittencourt prof.douglas.pucgo@gmail.com Tópicos abordados Coeficiente de empuxo em repouso Tensões
Equações de Navier-Stokes
 Equações de Navier-Stokes J. L. Baliño Escola Politécnica - Universidade de São Paulo Apostila de aula 2017, v. 1 Equações de Navier-Stokes 1 / 16 Sumário 1 Relações constitutivas 2 Conservação do momento
Equações de Navier-Stokes J. L. Baliño Escola Politécnica - Universidade de São Paulo Apostila de aula 2017, v. 1 Equações de Navier-Stokes 1 / 16 Sumário 1 Relações constitutivas 2 Conservação do momento
Apostila de Resistência dos Materiais II
 Departamento de Mecânica Aplicada e Computacional Faculdade de Engenharia Juiz de Fora - MG Apostila de Resistência dos Materiais II Prof. Elson Magalhães Toledo (emtc@lncc.br) Prof. Aleandre Cur (aleandre.cur@ufjf.edu.br)
Departamento de Mecânica Aplicada e Computacional Faculdade de Engenharia Juiz de Fora - MG Apostila de Resistência dos Materiais II Prof. Elson Magalhães Toledo (emtc@lncc.br) Prof. Aleandre Cur (aleandre.cur@ufjf.edu.br)
Aula 12. Ângulo entre duas retas no espaço. Definição 1. O ângulo (r1, r2 ) entre duas retas r1 e r2 se define da seguinte maneira:
 Aula 1 1. Ângulo entre duas retas no espaço Definição 1 O ângulo (r1, r ) entre duas retas r1 e r se define da seguinte maneira: (r1, r ) 0o se r1 e r são coincidentes, Se as retas são concorrentes, isto
Aula 1 1. Ângulo entre duas retas no espaço Definição 1 O ângulo (r1, r ) entre duas retas r1 e r se define da seguinte maneira: (r1, r ) 0o se r1 e r são coincidentes, Se as retas são concorrentes, isto
Transformação da deformação
 - UNIVERSIDADE FEDERAL FLUMINENSE ESCOLA DE ENGENHARIA INDUSTRIAL METALÚRGICA DE VOLTA REDONDA PROFESSORA: SALETE SOUZA DE OLIVEIRA BUFFONI DISCIPLINA: RESISTÊNCIA DOS MATERIAIS Transformação da deformação
- UNIVERSIDADE FEDERAL FLUMINENSE ESCOLA DE ENGENHARIA INDUSTRIAL METALÚRGICA DE VOLTA REDONDA PROFESSORA: SALETE SOUZA DE OLIVEIRA BUFFONI DISCIPLINA: RESISTÊNCIA DOS MATERIAIS Transformação da deformação
UNIVERSIDADE DE SÃO PAULO ESCOLA POLITÉCNICA
 UNIVERSIDADE DE SÃO PAULO ESCOLA POLITÉCNICA Departamento de Engenharia de Estruturas e Geotécnica CURSO BÁSICO DE RESISTÊNCIA DOS MATERIAIS FASCÍCULO Nº 9 Estado duplo de tensão. Círculo de Mohr H. Britto.015
UNIVERSIDADE DE SÃO PAULO ESCOLA POLITÉCNICA Departamento de Engenharia de Estruturas e Geotécnica CURSO BÁSICO DE RESISTÊNCIA DOS MATERIAIS FASCÍCULO Nº 9 Estado duplo de tensão. Círculo de Mohr H. Britto.015
LOM Teoria da Elasticidade Aplicada
 Departamento de Engenharia de Materiais (DEMAR) Escola de Engenharia de Lorena (EEL) Universidade de São Paulo (USP) LOM310 - Teoria da Elasticidade Aplicada Parte - Critérios de Falha Prof. Dr. João Paulo
Departamento de Engenharia de Materiais (DEMAR) Escola de Engenharia de Lorena (EEL) Universidade de São Paulo (USP) LOM310 - Teoria da Elasticidade Aplicada Parte - Critérios de Falha Prof. Dr. João Paulo
Resistência dos Materiais 2003/2004 Curso de Gestão e Engenharia Industrial
 1/9 Resistência dos Materiais 003/004 Curso de Gestão e Engenharia Industrial 5ª Aula Duração - Horas Data - 6 de Outubro de 003 Sumário: Caso Particular do Estado Plano de Tensão. Circunferência de Mohr.
1/9 Resistência dos Materiais 003/004 Curso de Gestão e Engenharia Industrial 5ª Aula Duração - Horas Data - 6 de Outubro de 003 Sumário: Caso Particular do Estado Plano de Tensão. Circunferência de Mohr.
Geometria Analítica. Cônicas. Prof Marcelo Maraschin de Souza
 Geometria Analítica Cônicas Prof Marcelo Maraschin de Souza É o lugar geométrico dos pontos de um plano cuja soma das distâncias a dois pontos fixos desse plano é constante. Considere dois pontos distintos
Geometria Analítica Cônicas Prof Marcelo Maraschin de Souza É o lugar geométrico dos pontos de um plano cuja soma das distâncias a dois pontos fixos desse plano é constante. Considere dois pontos distintos
UNIVERSIDADE FEDERAL DO PARÁ CÁLCULO II - PROJETO NEWTON AULA 04. v = x 2 + y 2. v = x1 x 2 + y 1 y 2. v = 0. v = x 2 + y 2 + z 2
 UNIVERSIDADE FEDERAL DO PARÁ CÁLCULO II - PROJETO NEWTON AULA 04 Assunto:Produto escalar, bases canônicas do R 2 e R 3, produto vetorial, produto misto, equação da reta no R 2 Palavras-chaves: Produto
UNIVERSIDADE FEDERAL DO PARÁ CÁLCULO II - PROJETO NEWTON AULA 04 Assunto:Produto escalar, bases canônicas do R 2 e R 3, produto vetorial, produto misto, equação da reta no R 2 Palavras-chaves: Produto
Resistência dos Materiais
 Resistência dos Materiais Prof. Antonio Dias Antonio Dias / Mecânica Geral I / Aula 8-1 Análise Estrutural Antonio Dias 2017 Antonio Dias / Mecânica Geral I / Aula 8-2 Objetivos do capítulo Mostrar como
Resistência dos Materiais Prof. Antonio Dias Antonio Dias / Mecânica Geral I / Aula 8-1 Análise Estrutural Antonio Dias 2017 Antonio Dias / Mecânica Geral I / Aula 8-2 Objetivos do capítulo Mostrar como
Resistência dos Materiais Eng. Mecânica, Produção UNIME Prof. Corey Lauro de Freitas, Fevereiro, 2016.
 Resistência dos Materiais Eng. Mecânica, Produção UNIME 2016.2 Prof. Corey Lauro de Freitas, Fevereiro, 2016. 1 Introdução: O conceito de tensão Conteúdo Conceito de Tensão Revisão de Estática Diagrama
Resistência dos Materiais Eng. Mecânica, Produção UNIME 2016.2 Prof. Corey Lauro de Freitas, Fevereiro, 2016. 1 Introdução: O conceito de tensão Conteúdo Conceito de Tensão Revisão de Estática Diagrama
Estado Duplo de Tensão
 Estado Duplo de Tensão Ps 13/12/95 2ª Questão Determinar graficamente as tensões principais ( σ 1 e σ 2 ) e as tensões de cisalhamento τ max e τ min, bem como a direção de seus planos de atuação, para
Estado Duplo de Tensão Ps 13/12/95 2ª Questão Determinar graficamente as tensões principais ( σ 1 e σ 2 ) e as tensões de cisalhamento τ max e τ min, bem como a direção de seus planos de atuação, para
Capítulo 3 GEOMETRIA DE MASSAS 3.1 INTRODUÇÃO 3.2 CENTRO DE MASSA E CENTRO DE GRAVIDADE
 Capítulo 3 EOMETR DE MSSS 3. NTRODUÇÃO Neste capítulo será feito o estudo de várias propriedades e características geométrico-mecânicas de linhas, superfícies e volumes, as quais constituirão uma ferramenta
Capítulo 3 EOMETR DE MSSS 3. NTRODUÇÃO Neste capítulo será feito o estudo de várias propriedades e características geométrico-mecânicas de linhas, superfícies e volumes, as quais constituirão uma ferramenta
Mecânica dos Sólidos I Parte 2
 Departamento de Engenharia Mecânica arte 2 rof. Arthur M. B. Braga 2006.1 arte II Barras carregadas axialmente (Cap. 1 e 2) Cisalhamento (Cap. 1) Torção de eixos cilíndricos (Cap. 3) Mecânica dos Sólidos
Departamento de Engenharia Mecânica arte 2 rof. Arthur M. B. Braga 2006.1 arte II Barras carregadas axialmente (Cap. 1 e 2) Cisalhamento (Cap. 1) Torção de eixos cilíndricos (Cap. 3) Mecânica dos Sólidos
massa do corpo A: m A ; massa do corpo B: m B ; massa da polia: M; raio da polia: R; adotando a aceleração da gravidade: g.
 Uma máquina de Atwood possui massas m A e m B, onde a massa B é maior que a massa A, ligadas por uma corda ideal, inextensível e de massa desprezível, através de uma polia de massa M e raio R. Determinar
Uma máquina de Atwood possui massas m A e m B, onde a massa B é maior que a massa A, ligadas por uma corda ideal, inextensível e de massa desprezível, através de uma polia de massa M e raio R. Determinar
raio do arco: a; ângulo central do arco: θ 0; carga do arco: Q.
 Sea um arco de circunferência de raio a e ângulo central carregado com uma carga distribuída uniformemente ao longo do arco. Determine: a) O vetor campo elétrico nos pontos da reta que passa pelo centro
Sea um arco de circunferência de raio a e ângulo central carregado com uma carga distribuída uniformemente ao longo do arco. Determine: a) O vetor campo elétrico nos pontos da reta que passa pelo centro
MATEMÁTICA A - 12o Ano N o s Complexos - Potências e raízes Propostas de resolução
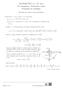 MATEMÁTICA A - 1o Ano N o s Complexos - Potências e raízes Propostas de resolução Exercícios de exames e testes intermédios 1. Escrevendo 1 + i na f.t. temos 1 + i ρ cis θ, onde: ρ 1 + i 1 + 1 1 + 1 tg
MATEMÁTICA A - 1o Ano N o s Complexos - Potências e raízes Propostas de resolução Exercícios de exames e testes intermédios 1. Escrevendo 1 + i na f.t. temos 1 + i ρ cis θ, onde: ρ 1 + i 1 + 1 1 + 1 tg
Capítulo 2 Tração, compressão e cisalhamento
 Capítulo 2 Tração, compressão e cisalhamento Resistência dos materiais I SLIDES 02 Prof. MSc. Douglas M. A. Bittencourt prof.douglas.pucgo@gmail.com 2.1 Cargas resultantes internas A distribuição de forças
Capítulo 2 Tração, compressão e cisalhamento Resistência dos materiais I SLIDES 02 Prof. MSc. Douglas M. A. Bittencourt prof.douglas.pucgo@gmail.com 2.1 Cargas resultantes internas A distribuição de forças
LOM Introdução à Mecânica dos Sólidos
 LOM 3081 - CAP. ANÁLISE DE TENSÃO E DEFORMAÇÃO PARTE 1 ANÁLISE DE TENSÃO VARIAÇÃO DA TENSÃO COM O PLANO DE CORTE Seja por exemplo uma barra sujeita a um carregamento axial. Ao aplicar o MÉTODO DAS SEÇÕES,
LOM 3081 - CAP. ANÁLISE DE TENSÃO E DEFORMAÇÃO PARTE 1 ANÁLISE DE TENSÃO VARIAÇÃO DA TENSÃO COM O PLANO DE CORTE Seja por exemplo uma barra sujeita a um carregamento axial. Ao aplicar o MÉTODO DAS SEÇÕES,
RESISTÊNCIA DOS MATERIAIS
 Terceira Edição CAPÍTULO RESISTÊNCIA DOS MATERIAIS Ferdinand P. Beer E. Russell Johnston, Jr. Análise de Tensões no Estado Plano Capítulo 6 Análise de Tensões no Estado Plano 6.1 Introdução 6. Estado Plano
Terceira Edição CAPÍTULO RESISTÊNCIA DOS MATERIAIS Ferdinand P. Beer E. Russell Johnston, Jr. Análise de Tensões no Estado Plano Capítulo 6 Análise de Tensões no Estado Plano 6.1 Introdução 6. Estado Plano
ESCOLA SECUNDÁRIA COM 3º CICLO D. DINIS 11º ANO DE ESCOLARIDADE DE MATEMÁTICA A TURMA A. TESTE Nº 2 Grupo I
 ESOL SEUNÁRI OM º ILO. INIS º NO E ESOLRIE E MTEMÁTI TURM TESTE Nº Grupo I s cinco questões deste grupo são de escolha múltipla. Para cada uma delas são indicadas quatro alternativas, das quais só uma
ESOL SEUNÁRI OM º ILO. INIS º NO E ESOLRIE E MTEMÁTI TURM TESTE Nº Grupo I s cinco questões deste grupo são de escolha múltipla. Para cada uma delas são indicadas quatro alternativas, das quais só uma
Dinâmica da partícula fluida
 Dinâmica da partícula fluida J. L. Baliño Escola Politécnica - Universidade de São Paulo Apostila de aula 2017, v.1 Dinâmica da partícula fluida 1 / 14 Sumário 1 Tipo de forças 2 Dinâmica da partícula
Dinâmica da partícula fluida J. L. Baliño Escola Politécnica - Universidade de São Paulo Apostila de aula 2017, v.1 Dinâmica da partícula fluida 1 / 14 Sumário 1 Tipo de forças 2 Dinâmica da partícula
Corpos Rígidos MOMENTO ANGULAR. Mecânica II (FIS-26) Prof. Dr. Ronaldo Rodrigues Pelá IEFF-ITA. 5 de março de R.R.Pelá
 MOMENTO ANGULAR Mecânica II (FIS-26) Prof. Dr. Ronaldo Rodrigues Pelá IEFF-ITA 5 de março de 2013 Roteiro 1 Roteiro 1 Quando todas as partículas de um corpo rígido se movem ao longo de trajetórias que
MOMENTO ANGULAR Mecânica II (FIS-26) Prof. Dr. Ronaldo Rodrigues Pelá IEFF-ITA 5 de março de 2013 Roteiro 1 Roteiro 1 Quando todas as partículas de um corpo rígido se movem ao longo de trajetórias que
Álgebra Linear I - Aula 3. Roteiro
 Álgebra Linear I - Aula 3 1. Produto escalar. Ângulos. 2. Desigualdade triangular. Roteiro 1 Produto escalar Considere dois vetores ū = (u 1, u 2, u 3 ) e v = (v 1, v 2, v 3 ) de R 3. O produto escalar
Álgebra Linear I - Aula 3 1. Produto escalar. Ângulos. 2. Desigualdade triangular. Roteiro 1 Produto escalar Considere dois vetores ū = (u 1, u 2, u 3 ) e v = (v 1, v 2, v 3 ) de R 3. O produto escalar
Sumário e Objectivos. Lúcia M.J.S. Dinis 2007/2008. Mecânica dos Sólidos Aula 5 1
 Sumário e Objectivos Sumário: Deformações sobre um plano. Valores Estacionários das Deformações. Compatibilidade das Deformações. Construção de Mohr para Deformações. Roseta de Extensómetros. Objectivos
Sumário e Objectivos Sumário: Deformações sobre um plano. Valores Estacionários das Deformações. Compatibilidade das Deformações. Construção de Mohr para Deformações. Roseta de Extensómetros. Objectivos
J. Delgado - K. Frensel - L. Crissaff Geometria Analítica e Cálculo Vetorial
 178 Capítulo 10 Equação da reta e do plano no espaço 1. Equações paramétricas da reta no espaço Sejam A e B dois pontos distintos no espaço e seja r a reta que os contém. Então, P r existe t R tal que
178 Capítulo 10 Equação da reta e do plano no espaço 1. Equações paramétricas da reta no espaço Sejam A e B dois pontos distintos no espaço e seja r a reta que os contém. Então, P r existe t R tal que
P1 de Álgebra Linear I
 P1 de Álgebra Linear I 2008.1 Gabarito 1) Decida se cada afirmação a seguir é verdadeira ou falsa e marque COM CANETA sua resposta no quadro a seguir. Itens V F N 1.a x 1.b x 1.c x 1.d x 1.e x 1.a) Para
P1 de Álgebra Linear I 2008.1 Gabarito 1) Decida se cada afirmação a seguir é verdadeira ou falsa e marque COM CANETA sua resposta no quadro a seguir. Itens V F N 1.a x 1.b x 1.c x 1.d x 1.e x 1.a) Para
Teorema da Divergência e Teorema de Stokes
 Teorema da Divergência e Teorema de tokes Resolução umária) 19 de Maio de 9 1. Calcule o fluxo do campo vectorial Fx, y, z) x, y, z) para fora da superfície {x, y, z) R 3 : x + y 1 + z, z 1}. a) Pela definição.
Teorema da Divergência e Teorema de tokes Resolução umária) 19 de Maio de 9 1. Calcule o fluxo do campo vectorial Fx, y, z) x, y, z) para fora da superfície {x, y, z) R 3 : x + y 1 + z, z 1}. a) Pela definição.
Álgebra Linear I - Aula 2. Roteiro
 Álgebra Linear I - Aula 2 1. Produto escalar. Ângulos. 2. Desigualdade triangular. 3. Projeção ortugonal de vetores. Roteiro 1 Produto escalar Considere dois vetores = (u 1, u 2, u 3 ) e v = (v 1, v 2,
Álgebra Linear I - Aula 2 1. Produto escalar. Ângulos. 2. Desigualdade triangular. 3. Projeção ortugonal de vetores. Roteiro 1 Produto escalar Considere dois vetores = (u 1, u 2, u 3 ) e v = (v 1, v 2,
Resistência dos Materiais 2003/2004 Curso de Gestão e Engenharia Industrial
 /8 Resistência dos Materiais 3/4 Curso de Gestão e Engenharia Industrial 8ª Aula Duração - Horas Data - 3 de Outubro de 3 Sumário: Energia de Deformação. Critérios de Cedência. Equações de Equilíbrio em
/8 Resistência dos Materiais 3/4 Curso de Gestão e Engenharia Industrial 8ª Aula Duração - Horas Data - 3 de Outubro de 3 Sumário: Energia de Deformação. Critérios de Cedência. Equações de Equilíbrio em
UNIVERSIDADE FEDERAL DE PERNAMBUCO
 CÁLCULO L1 NOTAS DA QUINTA AULA UNIVERSIDADE FEDERAL DE PERNAMBUCO Resumo. Iniciamos a aula definindo as funções trigonométricas e estabelecendo algumas de suas propriedades básicas. A seguir, calcularemos
CÁLCULO L1 NOTAS DA QUINTA AULA UNIVERSIDADE FEDERAL DE PERNAMBUCO Resumo. Iniciamos a aula definindo as funções trigonométricas e estabelecendo algumas de suas propriedades básicas. A seguir, calcularemos
Estado duplo ou, Estado plano de tensões.
 Estado duplo ou, Estado plano de tensões. tensão que atua em um ponto é função do plano pelo qual se faz o estudo. Esta afirmação pode ficar mais clara quando analisa, por exemplo, um ponto de uma barra
Estado duplo ou, Estado plano de tensões. tensão que atua em um ponto é função do plano pelo qual se faz o estudo. Esta afirmação pode ficar mais clara quando analisa, por exemplo, um ponto de uma barra
ESCOLA SECUNDÁRIA COM 3º CICLO D. DINIS 11º ANO DE ESCOLARIDADE DE MATEMÁTICA A Tema I Geometria no Plano e no Espaço II
 ESCOLA SECUNDÁRIA COM º CICLO D DINIS 11º ANO DE ESCOLARIDADE DE MATEMÁTICA A Tema I Geometria no Plano e no Espaço II Ficha de trabalho nº 4 1 Resolva o exercício 11 da página 80 do seu manual Considere
ESCOLA SECUNDÁRIA COM º CICLO D DINIS 11º ANO DE ESCOLARIDADE DE MATEMÁTICA A Tema I Geometria no Plano e no Espaço II Ficha de trabalho nº 4 1 Resolva o exercício 11 da página 80 do seu manual Considere
Capítulo 6 Transformação de tensão no plano
 Capítulo 6 Transformação de tensão no plano Resistência dos Materiais I SLIDES 06 Prof. MSc. Douglas M. A. Bittencourt prof.douglas.pucgo@gmail.com Objetivos do capítulo Transformar as componentes de tensão
Capítulo 6 Transformação de tensão no plano Resistência dos Materiais I SLIDES 06 Prof. MSc. Douglas M. A. Bittencourt prof.douglas.pucgo@gmail.com Objetivos do capítulo Transformar as componentes de tensão
massa do corpo A: m A ; massa do corpo B: m B ; massa da polia: M; raio da polia: R; adotando a aceleração da gravidade: g.
 Uma máquina de Atwood possui massas m A e m B, onde a massa B é maior que a massa A, ligadas por uma corda ideal, inextensível e de massa desprezível, através de uma polia de massa M e raio R. Determinar
Uma máquina de Atwood possui massas m A e m B, onde a massa B é maior que a massa A, ligadas por uma corda ideal, inextensível e de massa desprezível, através de uma polia de massa M e raio R. Determinar
Problema (flexão em 4 pontos)
 Problema (flexão em 4 pontos) Um provete cilíndrico de osso compacto, com um diâmetro exterior d e =3 mm e diâmetro interior d i =16 mm, está sujeito a um esforço de flexão em 4 pontos (ver figura, F=1
Problema (flexão em 4 pontos) Um provete cilíndrico de osso compacto, com um diâmetro exterior d e =3 mm e diâmetro interior d i =16 mm, está sujeito a um esforço de flexão em 4 pontos (ver figura, F=1
Capítulo 7 Transformações de Tensão e Deformação. O Círculo de Mohr. Grupo 9:
 Capítulo 7 Transformações de Tensão e Deformação O Círculo de Mohr André P. Santos Edward O. Schaden Pedro G. Rubira Túlio J. Silva Grupo 9: RA:070166 RA:060316 RA:073592 RA:072544 Transformação do Estado
Capítulo 7 Transformações de Tensão e Deformação O Círculo de Mohr André P. Santos Edward O. Schaden Pedro G. Rubira Túlio J. Silva Grupo 9: RA:070166 RA:060316 RA:073592 RA:072544 Transformação do Estado
6.1 equações canônicas de círculos e esferas
 6 C Í R C U LO S E E S F E R A S 6.1 equações canônicas de círculos e esferas Um círculo é o conjunto de pontos no plano que estão a uma certa distância r de um ponto dado (a, b). Desta forma temos que
6 C Í R C U LO S E E S F E R A S 6.1 equações canônicas de círculos e esferas Um círculo é o conjunto de pontos no plano que estão a uma certa distância r de um ponto dado (a, b). Desta forma temos que
Alexandre Nolasco de Carvalho Universidade de São Paulo São Carlos SP, Brazil. 13 de Março de 2014
 Funções - Aula 07 Alexandre Nolasco de Carvalho Universidade de São Paulo São Carlos SP, Brazil 13 de Março de 2014 Primeiro Semestre de 2014 Turma 2014106 - Engenharia Mecânica Funções Inversas Definição
Funções - Aula 07 Alexandre Nolasco de Carvalho Universidade de São Paulo São Carlos SP, Brazil 13 de Março de 2014 Primeiro Semestre de 2014 Turma 2014106 - Engenharia Mecânica Funções Inversas Definição
Teoria da Membrana. Cascas de Revolução 9.1. Capítulo 9
 Teoria da Membrana. Cascas de evolução 9. Capítulo 9 Teoria de Membrana. Cascas de evolução 9. Sistema de Eixos Uma casca de revolução tem uma superfície média que forma uma superfície de revolução. Esta
Teoria da Membrana. Cascas de evolução 9. Capítulo 9 Teoria de Membrana. Cascas de evolução 9. Sistema de Eixos Uma casca de revolução tem uma superfície média que forma uma superfície de revolução. Esta
Estabilidade. Conhecimentos Básicos
 Estabilidade Conhecimentos Básicos Unidades NOME SÍMBOLO FATOR MULTIPLICADOR (UND) Exa E 10 18 1 000 000 000 000 000 000 Peta P 10 15 1 000 000 000 000 000 Terá T 10 12 1 000 000 000 000 Giga G 10 9 1
Estabilidade Conhecimentos Básicos Unidades NOME SÍMBOLO FATOR MULTIPLICADOR (UND) Exa E 10 18 1 000 000 000 000 000 000 Peta P 10 15 1 000 000 000 000 000 Terá T 10 12 1 000 000 000 000 Giga G 10 9 1
( )( ) = =
 GABARITO IME MATEMÁTICA Questão Assinale a alternativa verdadeira: (A) 06 0 < 07 06
GABARITO IME MATEMÁTICA Questão Assinale a alternativa verdadeira: (A) 06 0 < 07 06
Módulo de Círculo Trigonométrico. Relação Fundamental da Trigonometria. 1 a série E.M.
 Módulo de Círculo Trigonométrico Relação Fundamental da Trigonometria a série EM Círculo Trigonométrico Relação Fundamental da Trigonometria Exercícios Introdutórios Exercício Se sen x /, determine Exercício
Módulo de Círculo Trigonométrico Relação Fundamental da Trigonometria a série EM Círculo Trigonométrico Relação Fundamental da Trigonometria Exercícios Introdutórios Exercício Se sen x /, determine Exercício
UNIVERSIDADE FEDERAL DE VIÇOSA DEPARTAMENTO DE MATEMÁTICA LISTA DE EXERCÍCIOS DE MAT243-CÁLCULO III
 UNIVERSIDADE FEDERAL DE VIÇOSA DEPARTAMENTO DE MATEMÁTICA LISTA DE EXERCÍCIOS DE MAT243-CÁLCULO III Capítulo 1 Vetores no Rn 1. Sejam u e v vetores tais que e u v = 2 e v = 1. Calcule v u v. 2. Sejam u
UNIVERSIDADE FEDERAL DE VIÇOSA DEPARTAMENTO DE MATEMÁTICA LISTA DE EXERCÍCIOS DE MAT243-CÁLCULO III Capítulo 1 Vetores no Rn 1. Sejam u e v vetores tais que e u v = 2 e v = 1. Calcule v u v. 2. Sejam u
1. (Espcex 2013) A figura geométrica formada pelos afixos das raízes complexas da equação a) 7 3 b) 6 3 c) 5 3 d) 4 3 e) 3 3
 Complexos 06. (Espcex 0) A figura geométrica formada pelos afixos das raízes complexas da equação a) 7 b) 6 c) 5 d) e) x 8 0 tem área igual a. (Unicamp 0) Chamamos de unidade imaginária e denotamos por
Complexos 06. (Espcex 0) A figura geométrica formada pelos afixos das raízes complexas da equação a) 7 b) 6 c) 5 d) e) x 8 0 tem área igual a. (Unicamp 0) Chamamos de unidade imaginária e denotamos por
2 Velocidade do Centro de Massa dos Elos
 Universidade Federal do Rio Grande do Sul Escola de Engenharia Departamento de Sistemas Elétricos de Automação e Energia ELE8 Robótica A 1 ntrodução Formulação de Lagrange-Euler Prof. Walter Fetter Lages
Universidade Federal do Rio Grande do Sul Escola de Engenharia Departamento de Sistemas Elétricos de Automação e Energia ELE8 Robótica A 1 ntrodução Formulação de Lagrange-Euler Prof. Walter Fetter Lages
UNIVERSIDADE ESTADUAL DE SANTA CRUZ UESC. 1 a Avaliação escrita de Cálculo IV Professor: Afonso Henriques Data: 10/04/2008
 1 a Avaliação escrita de Professor: Afonso Henriques Data: 10/04/008 1. Seja R a região do plano delimitada pelos gráficos de y = x, y = 3x 18 e y = 0. Se f é continua em R, exprima f ( x, y) da em termos
1 a Avaliação escrita de Professor: Afonso Henriques Data: 10/04/008 1. Seja R a região do plano delimitada pelos gráficos de y = x, y = 3x 18 e y = 0. Se f é continua em R, exprima f ( x, y) da em termos
UFABC - Universidade Federal do ABC. ESTO Mecânica dos Sólidos I. as deformações principais e direções onde elas ocorrem.
 UFABC - Universidade Federal do ABC ESTO008-13 Mecânica dos Sólidos I Sétima Lista de Exercícios Prof. Dr. Wesley Góis CECS Prof. Dr. Cesar Freire - CECS Estudo das Deformações 1. Segundo as direções a,b
UFABC - Universidade Federal do ABC ESTO008-13 Mecânica dos Sólidos I Sétima Lista de Exercícios Prof. Dr. Wesley Góis CECS Prof. Dr. Cesar Freire - CECS Estudo das Deformações 1. Segundo as direções a,b
Fluidos não Newtonianos na Indústria do Petróleo
 Fluidos não Newtonianos na Indústria do Petróleo Profa. Mônica F. Naccache naccache@puc-rio.br Sala 153-L, R 1174 http://naccache.usuarios.rdc.puc-rio.br/cursos/fnnip.html Introdução Reologia: ciência
Fluidos não Newtonianos na Indústria do Petróleo Profa. Mônica F. Naccache naccache@puc-rio.br Sala 153-L, R 1174 http://naccache.usuarios.rdc.puc-rio.br/cursos/fnnip.html Introdução Reologia: ciência
Sumário: Relações Tensões - Deformações. Energia de Deformação. Critérios de Cedência.
 Sumário e Objectivos Sumário: Relações Tensões - Deformações. Energia de Deformação. Critérios de Cedência. Objectivos da Aula: Ser Capaz de estabelecer e utilizar a lei de Hooke Generalizada. Fazer Controlo
Sumário e Objectivos Sumário: Relações Tensões - Deformações. Energia de Deformação. Critérios de Cedência. Objectivos da Aula: Ser Capaz de estabelecer e utilizar a lei de Hooke Generalizada. Fazer Controlo
Flexão. Tensões na Flexão. e seu sentido é anti-horário. Estudar a flexão em barras é estudar o efeito dos momentos fletores nestas barras.
 Flexão Estudar a flexão em barras é estudar o efeito dos momentos fletores nestas barras. O estudo da flexão que se inicia, será dividido, para fim de entendimento, em duas partes: Tensões na flexão; Deformações
Flexão Estudar a flexão em barras é estudar o efeito dos momentos fletores nestas barras. O estudo da flexão que se inicia, será dividido, para fim de entendimento, em duas partes: Tensões na flexão; Deformações
UFJF - Professores Elson Toledo e Alexandre Cury MAC003 - Resistência dos Materiais II LISTA DE EXERCÍCIOS 03
 UFJF - Professores Elson Toledo e Alexandre Cury MAC003 - Resistência dos Materiais II LISTA DE EXERCÍCIOS 03 1. Em um ponto crítico de uma peça de aço de uma máquina, as componentes de tensão encontradas
UFJF - Professores Elson Toledo e Alexandre Cury MAC003 - Resistência dos Materiais II LISTA DE EXERCÍCIOS 03 1. Em um ponto crítico de uma peça de aço de uma máquina, as componentes de tensão encontradas
Nome do aluno: N.º: Para responder aos itens de escolha múltipla, não apresente cálculos nem justificações e escreva, na folha de respostas:
 Teste de Matemática A 018 / 019 Teste N.º 1 Matemática A Duração do Teste (Caderno 1+ Caderno ): 90 minutos 11.º Ano de Escolaridade Nome do aluno: N.º: Turma: Este teste é constituído por dois cadernos:
Teste de Matemática A 018 / 019 Teste N.º 1 Matemática A Duração do Teste (Caderno 1+ Caderno ): 90 minutos 11.º Ano de Escolaridade Nome do aluno: N.º: Turma: Este teste é constituído por dois cadernos:
Nome do aluno: N.º: Para responder aos itens de escolha múltipla, não apresente cálculos nem justificações e escreva, na folha de respostas:
 Teste de Matemática A 017 / 018 Teste N.º 1 Matemática A Duração do Teste (Caderno 1+ Caderno ): 90 minutos 11.º Ano de Escolaridade Nome do aluno: N.º: Turma: Este teste é constituído por dois cadernos:
Teste de Matemática A 017 / 018 Teste N.º 1 Matemática A Duração do Teste (Caderno 1+ Caderno ): 90 minutos 11.º Ano de Escolaridade Nome do aluno: N.º: Turma: Este teste é constituído por dois cadernos:
LISTA 0 - GABARITO. ( n p )ap b n p, n N {0}. (Passo de indução) Suponhamos a fórmula válida para m N e provemo-la para m=1. = a
 Curso: MAT 43 - CÁLCULO para CIÊNCIAS BIOLÓGICAS - FCFUSP Professor Oswaldo Rio Branco de Oliveira Período: Primeiro Semestre de 200 LISTA 0 - GABARITO. Binômio de Newton (a+b) n pn p0 ( n p )ap b n p,
Curso: MAT 43 - CÁLCULO para CIÊNCIAS BIOLÓGICAS - FCFUSP Professor Oswaldo Rio Branco de Oliveira Período: Primeiro Semestre de 200 LISTA 0 - GABARITO. Binômio de Newton (a+b) n pn p0 ( n p )ap b n p,
Números Complexos 2017
 Números Complexos 07. (Eear 07) Se i é a unidade imaginária, então i i i é um número complexo que pode ser representado no plano de Argand-Gauss no quadrante. a) primeiro b) segundo c) terceiro d) quarto.
Números Complexos 07. (Eear 07) Se i é a unidade imaginária, então i i i é um número complexo que pode ser representado no plano de Argand-Gauss no quadrante. a) primeiro b) segundo c) terceiro d) quarto.
Disciplinas: Mecânica dos Materiais 2 6º Período E Dinâmica e Projeto de Máquinas 2-10º Período
 UNIVERSIDADE DO ESTADO DO RIO DE JANEIRO INSTITUTO POLITÉCNICO Graduação em Engenharia Mecânica Disciplinas: Mecânica dos Materiais 2 6º Período E Dinâmica e Projeto de Máquinas 2-10º Período Professor:
UNIVERSIDADE DO ESTADO DO RIO DE JANEIRO INSTITUTO POLITÉCNICO Graduação em Engenharia Mecânica Disciplinas: Mecânica dos Materiais 2 6º Período E Dinâmica e Projeto de Máquinas 2-10º Período Professor:
SIMULADO 3 INSTITUTO TECNOLÓGICO DE AERONÁUTICA VESTIBULAR 2018 GABARITO
 SIMULADO 3 INSTITUTO TECNOLÓGICO DE AERONÁUTICA VESTIBULAR 018 GABARITO Física Inglês Português Matemática 1 C 1 * 1 D 1 B B B E C 3 B 3 B 3 D 3 D 4 E 4 C 4 A 4 E 5 A 5 B 5 C 5 C 6 C 6 E 6 E 6 A 7 E 7
SIMULADO 3 INSTITUTO TECNOLÓGICO DE AERONÁUTICA VESTIBULAR 018 GABARITO Física Inglês Português Matemática 1 C 1 * 1 D 1 B B B E C 3 B 3 B 3 D 3 D 4 E 4 C 4 A 4 E 5 A 5 B 5 C 5 C 6 C 6 E 6 E 6 A 7 E 7
P4 de Cálculo a Várias Variáveis I MAT Data: 02 de julho
 P de Cálculo a Várias Variáveis I MAT 6 03. Data: 0 de julho Nome: Assinatura: Matrícula: Turma: Questão Valor Nota Revisão 5.0 5.0 Total 0.0 Instruções Mantenha seu celular desligado durante toda a prova.
P de Cálculo a Várias Variáveis I MAT 6 03. Data: 0 de julho Nome: Assinatura: Matrícula: Turma: Questão Valor Nota Revisão 5.0 5.0 Total 0.0 Instruções Mantenha seu celular desligado durante toda a prova.
FUNÇÕES TRIGONOMÉTRICAS. Teorema de Pitágoras Razões trigonométricas Circunferência trigonométrica
 FUNÇÕES TRIGONOMÉTRICAS Teorema de Pitágoras Razões trigonométricas Circunferência trigonométrica Teorema de Pitágoras Em qualquer triângulo retângulo, o quadrado da medida da hipotenusa é igual à soma
FUNÇÕES TRIGONOMÉTRICAS Teorema de Pitágoras Razões trigonométricas Circunferência trigonométrica Teorema de Pitágoras Em qualquer triângulo retângulo, o quadrado da medida da hipotenusa é igual à soma
01. Determinar as equações da reta que passa pelo ponto A( 2, 3, 2) e tem a. = 2x. v são: b c
 01. Determinar as equações da reta que passa pelo ponto A(, 3, ) e tem a direção do vetor v = 3 i + k. a = 3 As componentes do vetor v são: b = 0. c = Tendo em vista que b = 0, a reta se acha num plano
01. Determinar as equações da reta que passa pelo ponto A(, 3, ) e tem a direção do vetor v = 3 i + k. a = 3 As componentes do vetor v são: b = 0. c = Tendo em vista que b = 0, a reta se acha num plano
Nome do aluno: N.º: Para responder aos itens de escolha múltipla, não apresente cálculos nem justificações e escreva, na folha de respostas:
 Teste de Matemática A 2017 / 2018 Teste N.º 4 Matemática A Duração do Teste (Caderno 1+ Caderno 2): 90 minutos 11.º Ano de Escolaridade Nome do aluno: N.º: Turma: Este teste é constituído por dois cadernos:
Teste de Matemática A 2017 / 2018 Teste N.º 4 Matemática A Duração do Teste (Caderno 1+ Caderno 2): 90 minutos 11.º Ano de Escolaridade Nome do aluno: N.º: Turma: Este teste é constituído por dois cadernos:
Cinemática da partícula fluida
 Cinemática da partícula fluida J. L. Baliño Escola Politécnica - Universidade de São Paulo Apostila de aula 2017, v.1 Cinemática da partícula fluida 1 / 16 Sumário 1 Descrição do movimento 2 Cinemática
Cinemática da partícula fluida J. L. Baliño Escola Politécnica - Universidade de São Paulo Apostila de aula 2017, v.1 Cinemática da partícula fluida 1 / 16 Sumário 1 Descrição do movimento 2 Cinemática
Matemática Unidade I Álgebra Série 15 - Progressão geométrica. a 4 = a 1 q 3 54 = 2 q 3 q 3 = 27 q = 3. a 5 = a 1 q 4 a 5 = a 5 = 162
 0 a 4 = a q 3 54 = q 3 q 3 = 7 q = 3 a 5 = a q 4 a 5 = 3 4 a 5 = 6 Resposta: C 0 a 8 = a q 4 43 = 3 q6 3 5 3 = q 6 q 6 = 3 6 Como os termos são positivos, q > 0; assim: q = 3 a 5 = a q 3 a 5 = 3 33 a 5
0 a 4 = a q 3 54 = q 3 q 3 = 7 q = 3 a 5 = a q 4 a 5 = 3 4 a 5 = 6 Resposta: C 0 a 8 = a q 4 43 = 3 q6 3 5 3 = q 6 q 6 = 3 6 Como os termos são positivos, q > 0; assim: q = 3 a 5 = a q 3 a 5 = 3 33 a 5
n 2,
 1. Considere o polinômio P (x) = ax 3 + bx 2 + cx, com a, b, c R. Suponha que P satisfaz P (x + 1) P (x) = x 2, para todo x R. i. Calcule os valores de a, b e c. ii. Usando a propriedade acima, calcule
1. Considere o polinômio P (x) = ax 3 + bx 2 + cx, com a, b, c R. Suponha que P satisfaz P (x + 1) P (x) = x 2, para todo x R. i. Calcule os valores de a, b e c. ii. Usando a propriedade acima, calcule
Exercício 1: Encontre o ângulo emtre os vetores v e w em cada um dos seguintes:
 Universidade Federal do Paraná 2 semestre 2016. Algebra Linear Olivier Brahic Lista de exercícios 1 Ortogonalidade Exercícios da Seção 5.1 Exercício 1: Encontre o ângulo emtre os vetores v e w em cada
Universidade Federal do Paraná 2 semestre 2016. Algebra Linear Olivier Brahic Lista de exercícios 1 Ortogonalidade Exercícios da Seção 5.1 Exercício 1: Encontre o ângulo emtre os vetores v e w em cada
Aula Distância entre duas retas paralelas no espaço. Definição 1. Exemplo 1
 Aula 1 Sejam r 1 = P 1 + t v 1 t R} e r 2 = P 2 + t v 2 t R} duas retas no espaço. Se r 1 r 2, sabemos que r 1 e r 2 são concorrentes (isto é r 1 r 2 ) ou não se intersectam. Quando a segunda possibilidade
Aula 1 Sejam r 1 = P 1 + t v 1 t R} e r 2 = P 2 + t v 2 t R} duas retas no espaço. Se r 1 r 2, sabemos que r 1 e r 2 são concorrentes (isto é r 1 r 2 ) ou não se intersectam. Quando a segunda possibilidade
Nome do aluno: N.º: Para responder aos itens de escolha múltipla, não apresente cálculos nem justificações e escreva, na folha de respostas:
 Teste de Matemática A 2018 / 2019 Teste N.º 5 Matemática A Duração do Teste (Caderno 1 + Caderno 2): 90 minutos 11.º Ano de Escolaridade Nome do aluno: N.º: Turma: Este teste é constituído por dois cadernos:
Teste de Matemática A 2018 / 2019 Teste N.º 5 Matemática A Duração do Teste (Caderno 1 + Caderno 2): 90 minutos 11.º Ano de Escolaridade Nome do aluno: N.º: Turma: Este teste é constituído por dois cadernos:
Jorge M. V. Capela, Marisa V. Capela. Araraquara, SP
 Cônicas e Equações Quadráticas Jorge M. V. Capela, Marisa V. Capela Instituto de Química - UNESP Araraquara, SP capela@iq.unesp.br Araraquara, SP - 2017 1 Parábolas 2 3 4 5 Introdução Parábolas Parábolas
Cônicas e Equações Quadráticas Jorge M. V. Capela, Marisa V. Capela Instituto de Química - UNESP Araraquara, SP capela@iq.unesp.br Araraquara, SP - 2017 1 Parábolas 2 3 4 5 Introdução Parábolas Parábolas
(b) a quantidade de cloro no tanque no instante t;
 NOME: Universidade Federal do Rio de Janeiro Instituto de Matemtica Departamento de Mtodos Matemticos Gabarito da a Prova de Cálculo II - 06//0 a QUESTÃO : Um tanque possui 0 litros de solução com cloro
NOME: Universidade Federal do Rio de Janeiro Instituto de Matemtica Departamento de Mtodos Matemticos Gabarito da a Prova de Cálculo II - 06//0 a QUESTÃO : Um tanque possui 0 litros de solução com cloro
PROPOSTA DE RESOLUÇÃO DA PROVA DE MATEMÁTICA A DO ENSINO SECUNDÁRIO (CÓDIGO DA PROVA 635) 1ª FASE 23 DE JUNHO 2017 GRUPO I
 PROPOSTA DE RESOLUÇÃO DA PROVA DE MATEMÁTICA A DO ENSINO SECUNDÁRIO (CÓDIGO DA PROVA 635) ª FASE 3 DE JUNHO 07. GRUPO I Dado que os algarismos que são usados são os do conjunto {,, 3, 4, 5, 6, 7, 8, 9
PROPOSTA DE RESOLUÇÃO DA PROVA DE MATEMÁTICA A DO ENSINO SECUNDÁRIO (CÓDIGO DA PROVA 635) ª FASE 3 DE JUNHO 07. GRUPO I Dado que os algarismos que são usados são os do conjunto {,, 3, 4, 5, 6, 7, 8, 9
Lista 6: transformações lineares.
 Lista 6: transformações lineares. 1) Diga, justificando, quais das seguintes funções constituem transformações lineares. a) T : R 2 R 2 tal que T (x 1, x 2 ) = (x 1 + x 2, 3x 1 x 2 ) b) T : R 2 R 2 tal
Lista 6: transformações lineares. 1) Diga, justificando, quais das seguintes funções constituem transformações lineares. a) T : R 2 R 2 tal que T (x 1, x 2 ) = (x 1 + x 2, 3x 1 x 2 ) b) T : R 2 R 2 tal
Teoria das Estruturas I - Aula 07
 Teoria das Estruturas I - Aula 07 Arcos Isostáticos Definição e Tipos Casos Particulares de Arcos Equação do Arco Parabólico de 2º. Grau, Equação da Linha de Pressões e Arcos com Apoios Desnivelados Prof.
Teoria das Estruturas I - Aula 07 Arcos Isostáticos Definição e Tipos Casos Particulares de Arcos Equação do Arco Parabólico de 2º. Grau, Equação da Linha de Pressões e Arcos com Apoios Desnivelados Prof.
Série IV - Momento Angular (Resoluções Sucintas)
 Mecânica e Ondas, 0 Semestre 006-007, LEIC Série IV - Momento Angular (Resoluções Sucintas) 1. O momento angular duma partícula em relação à origem é dado por: L = r p a) Uma vez que no movimento uniforme
Mecânica e Ondas, 0 Semestre 006-007, LEIC Série IV - Momento Angular (Resoluções Sucintas) 1. O momento angular duma partícula em relação à origem é dado por: L = r p a) Uma vez que no movimento uniforme
Matemática 1 a QUESTÃO
 Matemática a QUESTÃO IME-007/008 Temos que: i) sen 3 x + cos 3 x = (senx + cosx) (sen x senxcosx + cos x) = (senx + cosx) ( senxcosx) ii) sen xcos x = ( + senxcosx) ( senxcosx) Então, a equação dada é
Matemática a QUESTÃO IME-007/008 Temos que: i) sen 3 x + cos 3 x = (senx + cosx) (sen x senxcosx + cos x) = (senx + cosx) ( senxcosx) ii) sen xcos x = ( + senxcosx) ( senxcosx) Então, a equação dada é
Material Teórico - Módulo: Vetores em R 2 e R 3. Módulo e Produto Escalar - Parte 1. Terceiro Ano - Médio
 Material Teórico - Módulo: Vetores em R 2 e R 3 Módulo e Produto Escalar - Parte 1 Terceiro Ano - Médio Autor: Prof. Angelo Papa Neto Revisor: Prof. Antonio Caminha M. Neto 1 Módulo de um vetor O módulo
Material Teórico - Módulo: Vetores em R 2 e R 3 Módulo e Produto Escalar - Parte 1 Terceiro Ano - Médio Autor: Prof. Angelo Papa Neto Revisor: Prof. Antonio Caminha M. Neto 1 Módulo de um vetor O módulo
Aula Orientação do espaço. Observação 1
 Aula 14 Nesta aula vamos definir dois novos produtos entre vetores do espaço, o produto vetorial e o produto misto. Para isso, primeiro vamos apresentar o conceito de orientação. 1. Orientação do espaço
Aula 14 Nesta aula vamos definir dois novos produtos entre vetores do espaço, o produto vetorial e o produto misto. Para isso, primeiro vamos apresentar o conceito de orientação. 1. Orientação do espaço
Capítulo 6 Círculo de Mohr para tensões
 Capítulo 6 Círculo de Mohr para tensões Resistência dos Materiais I SLIDES 07 Prof. MSc. Douglas M. A. Bittencourt prof.douglas.pucgo@gmail.com 6.4 Círculo de Mohr - Tensão no plano Consiste na solução
Capítulo 6 Círculo de Mohr para tensões Resistência dos Materiais I SLIDES 07 Prof. MSc. Douglas M. A. Bittencourt prof.douglas.pucgo@gmail.com 6.4 Círculo de Mohr - Tensão no plano Consiste na solução
