Geometria Analítica e Números Complexos DISCIPLINA. Estudando as quádricas. Autores. Cláudio Carlos Dias. Neuza Maria Dantas. aula
|
|
|
- Afonso Fortunato Lage
- 6 Há anos
- Visualizações:
Transcrição
1 DISCIPLINA Geometria Analítica e Números Complexos Estudando as quádricas Autores Cláudio Carlos Dias Neua Maria Dantas aula 15
2 Governo Federal Presidente da República Lui Inácio Lula da Silva Ministro da Educação Fernando Haddad Secretário de Educação a Distância SEED Ronaldo Motta Universidade Federal do Rio Grande do Norte Reitor José Ivonildo do Rêgo Vice-Reitor Nilsen Carvalho Fernandes de Oliveira Filho Secretária de Educação a Distância Vera Lúcia do Amaral Secretaria de Educação a Distância- SEDIS Coordenadora da Produção dos Materiais Célia Maria de Araújo Coordenador de Edição Ary Sergio Braga Olinisky Projeto Gráfico Ivana Lima Revisores de Estrutura e Linguagem Eugenio Tavares Borges Marcos Aurélio Felipe Revisora das Normas da ABNT Verônica Pinheiro da Silva Revisoras de Língua Portuguesa Janaina Toma Capistrano Sandra Cristinne Xavier da Câmara Revisora Tipográfica Nouraide Queiro Ilustradora Carolina Costa Editoração de Imagens Adauto Harley Carolina Costa Diagramadores Bruno de Soua Melo Adaptação para Módulo Matemático Thaisa Maria Simplício Lemos Pedro Gustavo Dias Diógenes Imagens Utiliadas Banco de Imagens Sedis (Secretaria de Educação a Distância) - UFRN Fotografias - Adauto Harley MasterClips IMSI MasterClips Collection, 1895 Francisco Blvd, East, San Rafael, CA 94901,USA. MasterFile MorgueFile Pixel Perfect Digital FreeImages FreeFoto.com Free Pictures Photos BigFoto FreeStockPhotos.com OneOddDude.net Stock.XCHG - Divisão de Serviços Técnicos Catalogação da publicação na Fonte. UFRN/Biblioteca Central Zila Mamede Dias, Cláudio Carlos. Geometria analítica e números complexos / Cláudio Carlos Dias, Neua Maria Dantas. Natal, RN : EDUFRN, p. : il 1. Geometria analítica plana. 2. Geometria analítica espacial. 3. Números complexos. I. Dantas, Neua Maria. II. Título. ISBN CDU RN/UF/BCZM 2006/88 CDD Todos os direitos reservados. Nenhuma parte deste material pode ser utiliada ou reproduida sem a autoriação expressa da UFRN - Universidade Federal do Rio Grande do Norte.
3 Apresentação Nas aulas 4 (A elipse), 5 (A parábola) e 6 (A hipérbole), você estudou as cônicas: elipse, parábola e hipérbole. Nesta aula, vamos estudar as quádricas, que são, no espaço, o similar às cônicas no plano. Estudaremos basicamente seus nove tipos. Objetivos Ao final desta aula, esperamos que você esteja apto a identificar e representar geometricamente uma quádrica a partir de sua equação e, reciprocamente, dar à equação de uma quádrica, conhecida sua representação geométrica. Aula 15 Geometria Analítica e Números Complexos 1
4 Quádricas Vamos analisar a seguir as equações que representam os nove tipos de quádricas, com a finalidade de representá-las geometricamente. Para tanto, examinaremos a interseção dessas superfícies, com planos x m, y l, k paralelos aos planos coordenados estudados na aula 14 (Planos no espaço tridimensional). Reconhecidas tais interseções, chamadas de seções, tentaremos remontar a superfície a partir das mesmas. Vamos estudar a seguir os nove tipos de quádricas. 1º O cilindro elíptico: Ao estudar, na aula 4, a equação no plano, você verificou que se trata de uma elipse com eixos nos eixos coordenados. Agora, se considerarmos essa mesma equação no espaço, significa que queremos analisar o conjunto de pontos (x,y,) do espaço tais que, note que a variável é independente de x e y. Ora, isso significa que qualquer plano k, paralelo ao plano xy, intercepta a superfície numa elipse nesse plano, de equação, ou seja, é sempre a mesma elipse, porém em diferentes planos paralelos ao plano xy. Isso significa que a superfície pode ser reconstruída unindo-se os pontos dessas elipses em planos paralelos ao plano xy, por retas paralelas (geratries do cilindro) ao eixo, conforme ilustrado na figura a seguir. Nesse caso, o eixo é dito o eixo do cilindro. Nota Observe que quando a b c a equação da elipse se torna a equação do círculo x y r. Nesse caso, o cilindro di-se circular reto. R> -b a -a b y x R< Figura 1 O cilindro elíptico: 2 Aula 15 Geometria Analítica e Números Complexos
5 Veja na Figura 1 que quando y, fica e, quando x, tem-se, que são as extremidades dos eixos da elipse em cada plano k. Exemplo 1 Identifique e esboce o gráfico da quádrica, de equação y. Solução Dividindo os dois membros por 36, obtemos, o que resulta, ou seja,. Isso di que a variável x é livre e para cada valor m de, é uma elipse no plano x m. Pelo que vimos anteriormente, trata-se de um cilindro elíptico com eixo igual ao eixo x exibido na figura a seguir. x m < x y x x m > Figura 2 O cilindro elíptico Aula 15 Geometria Analítica e Números Complexos 3
6 2º. O cilindro hiperbólico: Se fosse no plano, a equação anterior representaria uma hipérbole simétrica em relação ao eixo y, com vértices nos pontos a) e a. Acontece que, nesse caso, queremos o conjunto dos pontos (x,y,) do espaço tais que. Repetindo o procedimento usado no caso anterior, verifica-se que os planos k interceptam a superfície segundo a hipérbole de equação nesse plano. Isso significa que para recompor a superfície liga-se as diferentes hipérboles nos planos paralelos ao plano xy por retas paralelas ao eixo, conforme ilustrado na figura que se segue. k > k> k -a a k < x k Figura 3 O cilindro hiperbólico: Atividade 1 Identifique e esboce o gráfico da quádrica dada pela equação x y 4 Aula 15 Geometria Analítica e Números Complexos
7 3º. O cilindro parabólico: y ax ; a Como nos dois casos anteriores, essa equação no plano xy representa uma curva, no caso, uma parábola, com vértice na origem, e simétrica em relação ao eixo y. Acontece que queremos identificar o conjunto dos pontos (x,y,) do espaço tais que y ax para qualquer valor de. Aqui, o procedimento é análogo aos anteriores. Ou seja, os planos paralelos ao plano xy de equações k interceptam essa quádrica segundo a parábola da equação y ax nesses planos. De modo que para refaer a superfície da quádrica basta ligar os pontos dessas parábolas por retas paralelas ao eixo, conforme mostrado na seguinte figura. y x Figura 4 O cilindro parabólico: y ax ; a> Atividade 2 Identifique e esboce o gráfico da quádrica de equação x by, b >. Aula 15 Geometria Analítica e Números Complexos 5
8 4º. O cone elíptico: Vamos analisar as interseções dessa quádrica com planos paralelos ao plano xy, isto é, por planos constante. Vejamos que para k> teremos, ou ainda,. Essa equação representa no plano k uma elipse de semieixos ak e bk. Isso significa que, à medida que o plano = k se afasta do plano xy, essas elipses vão aumentando de eixos. Isto é, quanto maior o valor de k, maiores os eixos das elipses. Observamos que se tivermos k <, fica mas, k k donde representa, no plano k, uma elipse de semi-eixos ak e bk, significando que à medida que o plano = k se afasta do plano xy os eixos dessas elipses crescem. Em resumo, os planos k, k > ou k < interceptam a quádrica em elipses, de modo que quanto mais distante esse plano está do plano xy, maiores são os eixos de tais elipses. Quando 0, tem se, ou seja, x y, que é a origem. Isso mostra que o plano xy intercepta a superfície apenas na origem. Para saber onde essas elipses se apóiam, vejamos que o plano y de equação x intercepta a quádrica segundo a curva de equação ou seja,,, que representa um par de retas no plano, x, passando pela origem. 6 Aula 15 Geometria Analítica e Números Complexos
9 Feitas essas análises, o esboço da quádrica é dado na Figura 5. k > x k > k < x k < Figura 5 O cone elíptico: Nota Na equação do cilindro elíptico, quando a b r, tem-se que os planos k interceptam a quádrica segundo um círculo, nesses planos, de raios rk e centros no eixo, o que é fácil de comprovar. Nesse caso, o cone é dito circular ou de revolução. Atividade 3 Identifique e esboce a quádrica dada pela equação x y. 5º. O elipsóide: Comecemos observando que para um ponto x,y, pertencer ao elipsóide, necessariamente, a x a,b y b e c c. Isso é claro, pois se fosse x a ou x a, teríamos, Aula 15 Geometria Analítica e Números Complexos 7
10 logo, donde nenhum ponto x,y, com x a ou x a pode pertencer ao elipsóide. Do mesmo modo, pontos x,y, com y b ou y b, bem como c ou c, não podem pertencer ao elipsóide. Veja que quando, então e, para que esteja sobre o elipsóide, devemos ter y,, ou seja, e pertencem ao elipsóide.. De modo análogo, A análise anterior nos permite concluir que, qualquer plano k, k > c paralelo ao eixo xy, ou qualquer plano y l, l > b paralelo ao eixo x, ou ainda, qualquer plano x m, m > a paralelo ao plano y onde k ou k, y l ou y l, x m ou x m, não interceptam a quádrica. Enquanto os planos e interceptam o elipsóide em, e. Portanto, para: k, c k c, temos, ou, a condição c k c di que. Logo, a equação anterior pode ser escrita como, que é a equação de uma elipse no plano k; y l, b l b, temos 8 Aula 15 Geometria Analítica e Números Complexos
11 , ou ainda, que é a equação de uma elipse no plano y l ; x m, a m a ou seja,,, que é a equação de uma elipse no plano x m. Esse estudo nos permite esboçar o elipsóide na Figura 6, na qual destacamos apenas as seções y constante e constante. c k -a -b b y a y l y l -c y k x Figura 6 O elipsóide: Nota Quando a b c r, o elipsóide torna-se uma esfera x y r. Enquanto, se apenas dois dos valores a, b e c são iguais, o elipsóide é dito um esferóide ou um elipsóide de revolução. Aula 15 Geometria Analítica e Números Complexos 9
12 Atividade 4 Identifique a quádrica dada pela equação x y e esboce o seu gráfico. 6º. O hiperbolóide de uma folha: Faendo k, obtemos ou, ou ainda, que representa uma elipse de semi-eixos. Vejamos que quanto maior o valor de k, maior é o eixo da elipse. Geometricamente, isso significa que os planos paralelos ao plano xy, quanto mais afastados desse plano estão, interceptam a quádrica em elipses com eixos cada ve maiores. Por outro lado, se y, temos, que representa uma hipérbole simétrica em relação ao eixo x. Enquanto se x, temos, 10 Aula 15 Geometria Analítica e Números Complexos
13 que representa uma hipérbole simétrica em relação ao eixo y. Isso significa que as elipses obtidas pela interseção dos planos paralelos ao plano xy se apóiam nessas hipérboles, conforme ilustrado na figura que segue. k > -b a -a k > b y k' < x k' < Figura 7 O hiperbolóide de uma folha: Nota Veja que para a b r a equação do hiperbolóide de uma folha é, isso significa que os planos k o interceptam em círculos de raios e centros no eixo, localiados nesses planos, chamaremos a quádrica de hiperbolóide de revolução de uma folha. Atividade 5 Descreva a quádrica dada pela equação x y r e esboce o seu gráfico. 7º. O hiperbolóide de duas folhas: Reescrevendo essa equação como, Aula 15 Geometria Analítica e Números Complexos 11
14 temos que, pois. Donde c, ou seja, c ou c (isto é, c), o que equivale a dier que os planos k com k < c não interceptam a quádrica. Portanto, substituindo k com kc na equação da quádrica, obtemos ou ainda, que é a equação de uma elipse no plano k, cujos eixos crescem à medida que o plano de equação k se afasta do plano xy. Para descobrirmos em que curvas tais elipses se apóiam, basta ver que, quando x, a equação da quádrica torna-se, que é uma hipérbole de vértices,c e,c. Com essas informações, é possível esboçar o gráfico da quádrica representado na seguinte figura. x k y k y k' x k' Figura 8 O hiperbolóide de duas folhas: Nota Quando a b r, a equação do hiperbolóide de duas folhas fica Desse modo, os planos k, k >c interceptam essa quádrica 12 Aula 15 Geometria Analítica e Números Complexos
15 segundo círculos de raio e centro no eixo. Por isso, diemos tratar-se de um hiperbolóide de revolução de duas folhas. Atividade 6 Identifique a quádrica de equação e esboce o seu gráfico. 8º. O parabolóide elíptico: Como, segue-se que, isso mostra que os planos k com k <, paralelos aos planos xy, não interceptam a quádrica. Mas, para k com k 0, tem-se, logo, se k, vem que x e y, ou seja, o plano xy que é o plano intercepta a quádrica na origem, enquanto para k >, obtém-se, ou ainda, Aula 15 Geometria Analítica e Números Complexos 13
16 que representa uma elipse com semi-eixos e, isso significa que, quanto maior o valor de k, isto é, quanto mais os planos k se afastam do plano xy, maiores são os semi-eixos da elipse. Por outro lado, substituindo x na equação da quádrica, obtemos, a qual representa uma parábola simétrica em relação ao eixo, mostrando que as elipses obtidas anteriormente se apóiam nessa parábola. Essas informações nos permite representar o gráfico da quádrica pela figura seguinte. y, x = b k > k > y x Figura 9 O parabolóide elíptico: Nota Quando a b r, a equação do parabolóide torna-se r x y. Isso significa que os planos k, k > interceptam a superfície nos círculos dados nesses planos com centros no eixo e raios. Nesse caso, a quádrica é chamada de parabolóide de revolução. Atividade 7 Descreva a quádrica representada pela equação y x e esboce o seu gráfico. 14 Aula 15 Geometria Analítica e Números Complexos
17 9º. O parabolóide hiperbólico: Ao invés de começarmos com os planos k, como fiemos para as quádricas anteriores, é conveniente começarmos analisando as seções com os planos y l paralelos ao plano x. Nesse caso, a equação passa a ser, que representa em cada plano y l uma parábola de vértice com concavidade voltada para baixo. Por outro lado, faendo x na equação inicial, obtemos que representa no plano y uma parábola com vértice na origem e concavidade voltada para cima. Veja que a interseção dessa parábola com cada plano y l é o ponto, que é o vértice de cada parábola descrita anteriormente, proveniente da interseção do plano y l com a quádrica. Ora, sabemos que o vértice de uma parábola é seu ponto de máximo ou de mínimo, conforme a parábola esteja com a concavidade voltada para baixo ou para cima, respectivamente. Feita essa observação, podemos concluir que a superfície em questão é obtida dependurando-se, pelo vértice, cada parábola no plano y l, na parábola no plano y, conforme ilustrado na Figura 10. y l < x 0, = y b y y l < x y y l > y l > Figura 10 O parabolóide hiperbólico: Nota Na equação do parabolóide hiperbólico, quando k, k, fica, que é a equação de uma hipérbole nesse plano, simétrica em relação ao eixo x, se k >. Daí a origem do nome hiperbólico para qualificar o parabolóide. Aula 15 Geometria Analítica e Números Complexos 15
18 Essa superfície é muitas vees chamada de uma sela, devido a sua aparência lembrar uma sela de cavalo. Exemplo 2 Dar o nome e a equação da quádrica representada pela figura seguinte. - x, y -y, x y x Figura 11 Representação de uma quádrica Solução É só observar que o plano y secciona a quádrica segundo a parábola de equações, enquanto o plano x a secciona segundo a parábola de equação y. Isso di que a quádrica é o parabolóide hiperbólico de equação uma sela montada sobre o eixo x., que representa Atividade 8 Identifique e esboce o gráfico da quádrica dada pela equação. Indique no gráfico as hipérboles obtidas pela interseção dos planos y e y com essa quádrica. 16 Aula 15 Geometria Analítica e Números Complexos
19 Exercícios 1 Se o ponto P(x,y, está sobre um cone elíptico, mostre que P t tx,ty,t, t, ainda está sobre esse cone, isto é, que a reta que passa pela origem e pelo ponto P t está totalmente contida no cone. Faça uma figura representativa de tal situação. 2 Mostre que, se um cilindro tem seu eixo paralelo ao eixo e se Px,y, é um ponto nesse cilindro, então a reta que passa por P e é paralela ao eixo está contida no referido cilindro. Ilustre esse fato com uma figura. Translação de eixos Observando bem as figuras que representam os nove tipos de quádricas estudadas, vemos que quase todas têm uma espécie de centro na origem. Acontece que em muitos casos essa espécie de centro está deslocada da origem, como mostra o exemplo 3. Exemplo 3 Identifique e esboce o gráfico da quádrica dada pela equação Solução x x y y Vamos usar a técnica de completar os quadrados em cada uma das variáveis x, y e. Para x, temos x x x xx x x xx Aula 15 Geometria Analítica e Números Complexos 17
20 Para y, vem y y y yy y y 2 y (y Para, fica Substituindo essas expressões na equação inicial, obtemos x y ou ainda x y o que dá. Introduiremos um novo sistema de coordenadas x', y' e ', sendo x'x y'y '. Assim, ficamos com, ou seja,. Sabemos que essa equação representa um elipsóide de semi-eixos e no novo sistema de coordenadas com centro na origem. Enquanto no velho sistema de coordenadas, o centro é o ponto C. A figura seguinte representa essa quádrica. Figura 12 O elipsóide de equação x xy y 18 Aula 15 Geometria Analítica e Números Complexos
21 Nota Di-se que o sistema x', y', ' anterior foi obtido do sistema x, y, pela translação do vetor. De um modo geral, dado um sistema de coordenadas x, y,, se x', y', ' são tais que x' x h, y' y k, ' l, diemos que esse sistema de coordenadas é obtido do antigo pela translação do vetor h,k,l. Veja que se um vetor v tem coordenadas (x,y, no antigo sistema, então as coordenadas x',y',' do vetor v', no sistema novo e de mesma extremidade que v, são obtidas observando que vtv', sendoth,k,l no sistema antigo. Isso significa que x,y,h,k,lx',y','x'h, yk', ' ou seja, x x' h x x h y y' k y' y k ' l ' l, o que justifica o termo translação usado anteriormente. A figura a seguir descreve geometricamente essa discussão. x t v v y y x Figura 13 Translação de eixos coordenados Aula 15 Geometria Analítica e Números Complexos 19
22 Observação 1 Usando a técnica de completar os quadrados, vamos verificar que qualquer equação do tipo, sendo A, B e C, representa uma quádrica. De fato, somando-se os termos e a ambos os membros dessa equação, obtemos ou ainda mas. Feito isso, podemos escrever a equação inicial como. Seja, 20 Aula 15 Geometria Analítica e Números Complexos
23 então, Introduiremos o novo sistema de coordenadas x', y', ', sendo. e chamando a equação transforma-se na equação padrão de uma quádrica, a saber. Caso G', obtemos Ax' By' C', que representa também a equação padrão de uma quádrica. Observe que a translação de eixos do sistema x, y, para o sistema x', y', ' foi feita através do vetor. Continuando os exercícios 3 Identifique e esboce o gráfico das quádricas representadas pelas equações: a) y y b) x x c). Aula 15 Geometria Analítica e Números Complexos 21
24 Resumo Nesta aula, estudamos as quádricas que são análogas no espaço às cônicas no plano. Vimos também que qualquer equação do segundo grau nas variáveis x, y, sem termos do tipo x, xy ou yx representa um dos nove tipos de quádricas tratados aqui. Auto-avaliação 1 No cone elíptico de equação, identifique e esboce os gráficos das seções dessa quádrica com os planos que contêm o eixo, isto é, os planos de equação y kx. 2 Identifique e esboce a interseção dos planos paralelos ao plano xy, isto é, dos planos k, com o parabolóide hiperbólico de equação a>0, b>. Considere os casos em que k > 0, k = 0 ou k < 0. 3 Diga o nome e a equação da quádrica representada na Figura 14. Figura 14 Representação de uma quádrica 22 Aula 15 Geometria Analítica e Números Complexos
25 Sugestões para a resolução dos exercícios 1. Basta verificar que cada ponto P t satisfa a equação do cone. 2. Dedua que qualquer ponto sobre a reta que passa por Px,y, e é paralela ao eixo é do tipo x,y,t, t. 3. a) Complete os quadrados para concluir que se trata de um cilindro elíptico com eixo paralelo ao eixo x e centro no ponto. b) Complete o quadrado na variável x para obter a equação de um cilindro parabólico. c) Ao completar os quadrados em x, y,, aparece naturalmente a equação de um hiperbolóide de uma folha. Referência SIMMONS, George F. Cálculo com geometria analítica. São Paulo: Mcgraw Hill, v. Aula 15 Geometria Analítica e Números Complexos 23
26 Anotações 24 Aula 15 Geometria Analítica e Números Complexos
27
28
Geometria Analítica e Números Complexos DISCIPLINA. Planos no espaço tridimensional. Autores. Cláudio Carlos Dias. Neuza Maria Dantas.
 DISCIPLINA Geometria Analítica e Números Complexos Planos no espaço tridimensional Autores Cláudio Carlos Dias Neuza Maria Dantas aula 14 Governo Federal Presidente da República Luiz Inácio Lula da Silva
DISCIPLINA Geometria Analítica e Números Complexos Planos no espaço tridimensional Autores Cláudio Carlos Dias Neuza Maria Dantas aula 14 Governo Federal Presidente da República Luiz Inácio Lula da Silva
Geometria Analítica e Números Complexos DISCIPLINA. Retas e esferas no espaço tridimensional. Autores. Cláudio Carlos Dias. Neuza Maria Dantas.
 DISCIPLINA Geometria Analítica e Números Complexos Retas e esferas no espaço tridimensional Autores Cláudio Carlos Dias Neuza Maria Dantas aula 13 Governo Federal Presidente da República Luiz Inácio Lula
DISCIPLINA Geometria Analítica e Números Complexos Retas e esferas no espaço tridimensional Autores Cláudio Carlos Dias Neuza Maria Dantas aula 13 Governo Federal Presidente da República Luiz Inácio Lula
Geometria Analítica e Números Complexos DISCIPLINA. Produto escalar. Autores. Cláudio Carlos Dias. Neuza Maria Dantas. aula
 DISCIPLINA Geometria Analítica e Números Complexos Produto escalar Autores Cláudio Carlos Dias Neuza Maria Dantas aula 11 Governo Federal Presidente da República Luiz Inácio Lula da Silva Ministro da Educação
DISCIPLINA Geometria Analítica e Números Complexos Produto escalar Autores Cláudio Carlos Dias Neuza Maria Dantas aula 11 Governo Federal Presidente da República Luiz Inácio Lula da Silva Ministro da Educação
aula Ligações covalentes formas moleculares e hibridização Autores 2ª Edição D I S C I P L I N A Arquitetura Atômica e Molecular
 2ª Edição D I S C I P L I N A Arquitetura Atômica e Molecular Ligações covalentes formas moleculares e hibridização Autores Ótom Anselmo de Oliveira Joana D Arc Gomes Fernandes aula 09 Material APROVADO
2ª Edição D I S C I P L I N A Arquitetura Atômica e Molecular Ligações covalentes formas moleculares e hibridização Autores Ótom Anselmo de Oliveira Joana D Arc Gomes Fernandes aula 09 Material APROVADO
Geometria Analítica e Números Complexos DISCIPLINA. Produto vetorial e produto misto. Autores. Cláudio Carlos Dias. Neuza Maria Dantas.
 DISCIPLINA Geometria Analítica e Números Complexos Produto vetorial e produto misto Autores Cláudio Carlos Dias Neuza Maria Dantas aula 12 Governo Federal Presidente da República Luiz Inácio Lula da Silva
DISCIPLINA Geometria Analítica e Números Complexos Produto vetorial e produto misto Autores Cláudio Carlos Dias Neuza Maria Dantas aula 12 Governo Federal Presidente da República Luiz Inácio Lula da Silva
Geometria Analítica e Números Complexos D I S C I P L I N A. A hipérbole. Autores. Cláudio Carlos Dias. Neuza Maria Dantas. aula
 D I S C I P L I N A Geometria Analítica e Números Complexos A hipérbole Autores Cláudio Carlos Dias Neuza Maria Dantas aula 06 Governo Federal Presidente da República Luiz Inácio Lula da Silva Ministro
D I S C I P L I N A Geometria Analítica e Números Complexos A hipérbole Autores Cláudio Carlos Dias Neuza Maria Dantas aula 06 Governo Federal Presidente da República Luiz Inácio Lula da Silva Ministro
Geometria Analítica e Números Complexos D I S C I P L I N A. A parábola. Autores. Cláudio Carlos Dias. Neuza Maria Dantas. aula
 D I S C I P L I N A Geometria Analítica e Números Complexos A parábola Autores Cláudio Carlos Dias Neuza Maria Dantas aula 05 Governo Federal Presidente da República Luiz Inácio Lula da Silva Ministro
D I S C I P L I N A Geometria Analítica e Números Complexos A parábola Autores Cláudio Carlos Dias Neuza Maria Dantas aula 05 Governo Federal Presidente da República Luiz Inácio Lula da Silva Ministro
Superfícies e Curvas no Espaço
 Superfícies e Curvas no Espaço Reginaldo J. Santos Departamento de Matemática-ICE Universidade Federal de Minas Gerais http://www.mat.ufmg.br/~regi regi@mat.ufmg.br 11 de deembro de 2001 1 Quádricas Nesta
Superfícies e Curvas no Espaço Reginaldo J. Santos Departamento de Matemática-ICE Universidade Federal de Minas Gerais http://www.mat.ufmg.br/~regi regi@mat.ufmg.br 11 de deembro de 2001 1 Quádricas Nesta
Aula 18 Cilindros quádricos e identificação de quádricas
 MÓDULO 2 - AULA 18 Aula 18 Cilindros quádricos e identificação de quádricas Objetivos Estudar os cilindros quádricos, analisando suas seções planas paralelas aos planos coordenados e estabelecendo suas
MÓDULO 2 - AULA 18 Aula 18 Cilindros quádricos e identificação de quádricas Objetivos Estudar os cilindros quádricos, analisando suas seções planas paralelas aos planos coordenados e estabelecendo suas
SUPERFÍCIES QUÁDRICAS
 1 SUPERFÍCIES QUÁDRICAS Dá-se o nome de superfície quádrica ou simplesmente quádrica ao gráfico de uma equação do segundo grau, nas variáveis, e, da forma: A + B + C + D + E + F + G + H + I + K = 0, que
1 SUPERFÍCIES QUÁDRICAS Dá-se o nome de superfície quádrica ou simplesmente quádrica ao gráfico de uma equação do segundo grau, nas variáveis, e, da forma: A + B + C + D + E + F + G + H + I + K = 0, que
SECÇÕES CÔNICAS E SUPERFÍCIES QUÁDRICAS Prof. Vasco Ricardo Aquino da Silva
 SECÇÕES CÔNICAS E SUPERFÍCIES QUÁDRICAS Prof. Vasco Ricardo Aquino da Silva SECÇÕES CÔNICAS Usando o programa winplot visualize as cônicas disponíveis em nosso AVA Moodle. 1. Elementos da Elipse: F1, F2:
SECÇÕES CÔNICAS E SUPERFÍCIES QUÁDRICAS Prof. Vasco Ricardo Aquino da Silva SECÇÕES CÔNICAS Usando o programa winplot visualize as cônicas disponíveis em nosso AVA Moodle. 1. Elementos da Elipse: F1, F2:
Informática e Educação. 2ª Edição DISCIPLINA. Navegando pelo Moodle. Autores. Apuena Vieira Gomes. Adja Ferreira de Andrade. aula
 2ª Edição DISCIPLINA Informática e Educação Navegando pelo Moodle Autores Apuena Vieira Gomes Adja Ferreira de Andrade aula 07 Governo Federal Presidente da República Luiz Inácio Lula da Silva Ministro
2ª Edição DISCIPLINA Informática e Educação Navegando pelo Moodle Autores Apuena Vieira Gomes Adja Ferreira de Andrade aula 07 Governo Federal Presidente da República Luiz Inácio Lula da Silva Ministro
21 e 22. Superfícies Quádricas. Sumário
 21 e 22 Superfícies uádricas Sumário 21.1 Introdução....................... 2 21.2 Elipsoide........................ 3 21.3 Hiperboloide de uma Folha.............. 4 21.4 Hiperboloide de duas folhas..............
21 e 22 Superfícies uádricas Sumário 21.1 Introdução....................... 2 21.2 Elipsoide........................ 3 21.3 Hiperboloide de uma Folha.............. 4 21.4 Hiperboloide de duas folhas..............
Geometria Analítica e Números Complexos D I S C I P L I N A. A elipse. Autores. Cláudio Carlos Dias. Neuza Maria Dantas. aula
 D I S C I P L I N A Geometria Analítica e Números Complexos A elipse Autores Cláudio Carlos Dias Neuza Maria Dantas aula 04 Governo Federal Presidente da República Luiz Inácio Lula da Silva Ministro da
D I S C I P L I N A Geometria Analítica e Números Complexos A elipse Autores Cláudio Carlos Dias Neuza Maria Dantas aula 04 Governo Federal Presidente da República Luiz Inácio Lula da Silva Ministro da
UNIVERSIDADE FEDERAL DE ALAGOAS INSTITUTO DE MATEMÁTICA Aluno(a): Professor(a): Curso:
 5 Geometria Analítica - a Avaliação - 6 de setembro de 0 Justique todas as suas respostas.. Dados os vetores u = (, ) e v = (, ), determine os vetores m e n tais que: { m n = u, v u + v m + n = P roj u
5 Geometria Analítica - a Avaliação - 6 de setembro de 0 Justique todas as suas respostas.. Dados os vetores u = (, ) e v = (, ), determine os vetores m e n tais que: { m n = u, v u + v m + n = P roj u
c) F( 4, 2) r : 2x+y = 3 c) a = 3 F 1 = (0,0) F 2 = (1,1)
 Lista de Exercícios Estudo Analítico das Cônicas e Quádricas 1. Determine o foco, o vértice, o parâmetro e a diretriz da parábola P e faça um esboço. a) P : y 2 = 4x b) P : y 2 +8x = 0 c) P : x 2 +6y =
Lista de Exercícios Estudo Analítico das Cônicas e Quádricas 1. Determine o foco, o vértice, o parâmetro e a diretriz da parábola P e faça um esboço. a) P : y 2 = 4x b) P : y 2 +8x = 0 c) P : x 2 +6y =
Geometria Analítica e Números Complexos D I S C I P L I N A. Estudando a reta no plano. Autores. Cláudio Carlos Dias. Neuza Maria Dantas.
 D I S C I P L I N A Geometria Analítica e Números Complexos Estudando a reta no plano Autores Cláudio Carlos Dias Neuza Maria Dantas aula 0 Governo Federal Presidente da República Luiz Inácio Lula da Silva
D I S C I P L I N A Geometria Analítica e Números Complexos Estudando a reta no plano Autores Cláudio Carlos Dias Neuza Maria Dantas aula 0 Governo Federal Presidente da República Luiz Inácio Lula da Silva
Universidade Tecnológica Federal do Paraná Câmpus Campo Mourão Departamento de Matemática
 Universidade Tecnológica Federal do Paraná Câmpus Campo Mourão Departamento de Matemática GAX1 - Geometria Analítica e Álgebra Linear Lista de Exercícios: Estudo Analítico de Cônicas e Quádricas Prof.
Universidade Tecnológica Federal do Paraná Câmpus Campo Mourão Departamento de Matemática GAX1 - Geometria Analítica e Álgebra Linear Lista de Exercícios: Estudo Analítico de Cônicas e Quádricas Prof.
Questão 2: Considere a hipérbole descrita pela equação 9x 2 16y 2 = 144. vértices, focos e esboce seu gráco.
 Ministério da Educação Universidade Tecnológica Federal do Paraná Campus Curitiba - DAMAT MA71B - Geometria Analítica e Álgebra Linear Prof a Dr a Diane Rizzotto Rossetto LISTA 8 - Cônicas e Quádricas
Ministério da Educação Universidade Tecnológica Federal do Paraná Campus Curitiba - DAMAT MA71B - Geometria Analítica e Álgebra Linear Prof a Dr a Diane Rizzotto Rossetto LISTA 8 - Cônicas e Quádricas
Capítulo 3 - Geometria Analítica
 1. Gráficos de Equações Capítulo 3 - Geometria Analítica Conceito:O gráfico de uma equação é o conjunto de todos os pontos e somente estes pontos, cujas coordenadas satisfazem a equação. Assim, o gráfico
1. Gráficos de Equações Capítulo 3 - Geometria Analítica Conceito:O gráfico de uma equação é o conjunto de todos os pontos e somente estes pontos, cujas coordenadas satisfazem a equação. Assim, o gráfico
c) F( 4, 2) r : 2x+y = 3 c) a = 3 F 1 = (0,0) F 2 = (1,1)
 Lista de Exercícios Estudo Analítico das Cônicas e Quádricas 1. Determine o foco, o vértice, o parâmetro e a diretriz da parábola P e faça um esboço. a) P : y 2 = 4x b) P : y 2 +8x = 0 c) P : x 2 +6y =
Lista de Exercícios Estudo Analítico das Cônicas e Quádricas 1. Determine o foco, o vértice, o parâmetro e a diretriz da parábola P e faça um esboço. a) P : y 2 = 4x b) P : y 2 +8x = 0 c) P : x 2 +6y =
4.1 Superfície Cilíndrica
 4.1 Superfície Cilíndrica Uma superfície cilíndrica (ou simplesmente cilindro) é a superfície gerada por uma reta que se move ao longo de uma curva plana, denominada diretriz, paralelamente a uma reta
4.1 Superfície Cilíndrica Uma superfície cilíndrica (ou simplesmente cilindro) é a superfície gerada por uma reta que se move ao longo de uma curva plana, denominada diretriz, paralelamente a uma reta
Cilindros projetantes de uma curva
 Cilindros projetantes de uma curva Dada uma curva C no espaço é possível obter tres cilindros retos cujas interseções fornecem a curva C. Estes cilindros são obtidos projetando-se a curva em cada um dos
Cilindros projetantes de uma curva Dada uma curva C no espaço é possível obter tres cilindros retos cujas interseções fornecem a curva C. Estes cilindros são obtidos projetando-se a curva em cada um dos
Geometria Analítica II - Aula
 Geometria Analítica II - Aula 0 94 Aula Coordenadas Cilíndricas e Esféricas Para descrever de modo mais simples algumas curvas e regiões no plano introduzimos anteriormente as coordenadas polares. No espaço
Geometria Analítica II - Aula 0 94 Aula Coordenadas Cilíndricas e Esféricas Para descrever de modo mais simples algumas curvas e regiões no plano introduzimos anteriormente as coordenadas polares. No espaço
x 2 a 2 + y2 c 2 = 1, b 2 + z2 Esta superfície é simétrica relativamente a cada um dos planos coordenados e relativamente
 Capítulo 2 Cálculo integral 2.1 Superfícies quádricas Uma superfície quádrica é um subconjunto de R 3 constituído por todos os pontos de R 3 que satisfazem uma equação com a forma A + B + Cz 2 + Dxy +
Capítulo 2 Cálculo integral 2.1 Superfícies quádricas Uma superfície quádrica é um subconjunto de R 3 constituído por todos os pontos de R 3 que satisfazem uma equação com a forma A + B + Cz 2 + Dxy +
Álgebra Linear e Geometria Anaĺıtica. Cónicas e Quádricas
 universidade de aveiro departamento de matemática Álgebra Linear e Geometria Anaĺıtica Agrupamento IV (ECT, EET, EI) Capítulo 6 Cónicas e Quádricas Equação geral de uma cónica [6 01] As cónicas são curvas
universidade de aveiro departamento de matemática Álgebra Linear e Geometria Anaĺıtica Agrupamento IV (ECT, EET, EI) Capítulo 6 Cónicas e Quádricas Equação geral de uma cónica [6 01] As cónicas são curvas
MAT Poli Roteiro de Estudos sobre as Cônicas
 MAT25 - Poli - 2003 Roteiro de Estudos sobre as Cônicas Martha Salerno Monteiro Departamento de Matemática IME-USP Uma equação quadrática em duas variáveis é uma equação da forma a + by 2 + cxy + dx +
MAT25 - Poli - 2003 Roteiro de Estudos sobre as Cônicas Martha Salerno Monteiro Departamento de Matemática IME-USP Uma equação quadrática em duas variáveis é uma equação da forma a + by 2 + cxy + dx +
(b) O centro é O, os focos estão em Oy, o eixo maior mede 10, e a distância focal é 6.
 Ministério da Educação Universidade Tecnológica Federal do Paraná Campus Campo Mourão Wellington José Corrêa Nome: 4 ā Lista de Geometria Analítica e Álgebra Linear No que segue, todas as bases utilizadas
Ministério da Educação Universidade Tecnológica Federal do Paraná Campus Campo Mourão Wellington José Corrêa Nome: 4 ā Lista de Geometria Analítica e Álgebra Linear No que segue, todas as bases utilizadas
MAT Poli Cônicas - Parte I
 MAT2454 - Poli - 2011 Cônicas - Parte I Uma equação quadrática em duas variáveis, x e y, é uma equação da forma ax 2 +by 2 +cxy +dx+ey +f = 0, em que pelo menos um doscoeficientes a, b oucénão nulo 1.
MAT2454 - Poli - 2011 Cônicas - Parte I Uma equação quadrática em duas variáveis, x e y, é uma equação da forma ax 2 +by 2 +cxy +dx+ey +f = 0, em que pelo menos um doscoeficientes a, b oucénão nulo 1.
GEOMETRIA ANALÍTICA E CÁLCULO VETORIAL GEOMETRIA ANALÍTICA BÁSICA. 03/01/ GGM - UFF Dirce Uesu Pesco
 GEOMETRIA ANALÍTICA E CÁLCULO VETORIAL GEOMETRIA ANALÍTICA BÁSICA 03/01/2013 - GGM - UFF Dirce Uesu Pesco CÔNICAS Equação geral do segundo grau a duas variáveis x e y onde A, B e C não são simultaneamente
GEOMETRIA ANALÍTICA E CÁLCULO VETORIAL GEOMETRIA ANALÍTICA BÁSICA 03/01/2013 - GGM - UFF Dirce Uesu Pesco CÔNICAS Equação geral do segundo grau a duas variáveis x e y onde A, B e C não são simultaneamente
Aula 15 Superfícies quádricas - cones quádricos
 Aula 15 Superfícies quádricas - cones quádricos MÓDULO - AULA 15 Objetivos Definir e estudar os cones quádricos identificando suas seções planas. Analisar os cones quádricos regrados e de revolução. Cones
Aula 15 Superfícies quádricas - cones quádricos MÓDULO - AULA 15 Objetivos Definir e estudar os cones quádricos identificando suas seções planas. Analisar os cones quádricos regrados e de revolução. Cones
PLANO DE ENSINO IDENTIFICAÇÃO DA DISCIPLINA
 1 PLANO DE ENSINO IDENTIFICAÇÃO DA DISCIPLINA Curso: CST em Sistemas de Telecomunicações, Tecnologia Nome da disciplina: Álgebra Vetorial Código: CEE.002 Carga horária: 67 horas Semestre previsto: 1 Pré-requisito(s):
1 PLANO DE ENSINO IDENTIFICAÇÃO DA DISCIPLINA Curso: CST em Sistemas de Telecomunicações, Tecnologia Nome da disciplina: Álgebra Vetorial Código: CEE.002 Carga horária: 67 horas Semestre previsto: 1 Pré-requisito(s):
Aula 19 Elipse - continuação
 MÓDULO 1 - AULA 19 Aula 19 Elipse - continuação Objetivos Desenhar a elipse com compasso e régua com escala. Determinar a equação reduzida da elipse no sistema de coordenadas com origem no ponto médio
MÓDULO 1 - AULA 19 Aula 19 Elipse - continuação Objetivos Desenhar a elipse com compasso e régua com escala. Determinar a equação reduzida da elipse no sistema de coordenadas com origem no ponto médio
Ricardo Bianconi. Fevereiro de 2015
 Seções Cônicas Ricardo Bianconi Fevereiro de 2015 Uma parte importante da Geometria Analítica é o estudo das curvas planas e, em particular, das cônicas. Neste texto estudamos algumas propriedades das
Seções Cônicas Ricardo Bianconi Fevereiro de 2015 Uma parte importante da Geometria Analítica é o estudo das curvas planas e, em particular, das cônicas. Neste texto estudamos algumas propriedades das
A primeira coisa a fazer é saber quais são as equações das curvas quando elas já se encontram na melhor
 Identificação de Cônicas Uma equação do segundo grau ax + bxy + cy + dx + ey + f = 0 define de maneira implícita uma curva no plano xy: o conjunto dos pontos (x, y) que satisfazem a equação. Por exemplo,
Identificação de Cônicas Uma equação do segundo grau ax + bxy + cy + dx + ey + f = 0 define de maneira implícita uma curva no plano xy: o conjunto dos pontos (x, y) que satisfazem a equação. Por exemplo,
Aula 8 Cônicas - Translação de sistemas de coordenadas
 Aula 8 Cônicas - Translação de sistemas de coordenadas MÓDULO 1 - AULA 8 Objetivos Entender a mudança de coordenadas pela translação do sistema cartesiano. Identificar uma cônica transladada a partir da
Aula 8 Cônicas - Translação de sistemas de coordenadas MÓDULO 1 - AULA 8 Objetivos Entender a mudança de coordenadas pela translação do sistema cartesiano. Identificar uma cônica transladada a partir da
APLICAÇÕES NA GEOMETRIA ANALÍTICA
 4 APLICAÇÕES NA GEOMETRIA ANALÍTICA Gil da Costa Marques 4.1 Geometria Analítica e as Coordenadas Cartesianas 4. Superfícies 4..1 Superfícies planas 4.. Superfícies limitadas e não limitadas 4.3 Curvas
4 APLICAÇÕES NA GEOMETRIA ANALÍTICA Gil da Costa Marques 4.1 Geometria Analítica e as Coordenadas Cartesianas 4. Superfícies 4..1 Superfícies planas 4.. Superfícies limitadas e não limitadas 4.3 Curvas
Obter as equações paramétricas das cônicas.
 MÓDULO 1 - AULA 1 Aula 1 Equações paramétricas das cônicas Objetivo Obter as equações paramétricas das cônicas. Estudando as retas no plano, você viu que a reta s, determinada pelos pontos P = (x 1, y
MÓDULO 1 - AULA 1 Aula 1 Equações paramétricas das cônicas Objetivo Obter as equações paramétricas das cônicas. Estudando as retas no plano, você viu que a reta s, determinada pelos pontos P = (x 1, y
CÔNICAS NÃO DEGENERADAS Cônicas 3 CÔNICAS Estudaremos as (seções) cônicas, curvas planas que são obtidas da intersecção de um cone circular com um pla
 CÔNICAS CLASSIFICAÇÃO DE CÔNICAS Cônicas CÔNICAS NÃO DEGENERADAS Cônicas 3 CÔNICAS Estudaremos as (seções) cônicas, curvas planas que são obtidas da intersecção de um cone circular com um plano. Cônicas
CÔNICAS CLASSIFICAÇÃO DE CÔNICAS Cônicas CÔNICAS NÃO DEGENERADAS Cônicas 3 CÔNICAS Estudaremos as (seções) cônicas, curvas planas que são obtidas da intersecção de um cone circular com um plano. Cônicas
TÓPICO. Fundamentos da Matemática II APLICAÇÕES NA GEOMETRIA ANALÍTICA. Licenciatura em Ciências USP/ Univesp. Gil da Costa Marques
 APLICAÇÕES NA GEOMETRIA ANALÍTICA 4 Gil da Costa Marques TÓPICO Fundamentos da Matemática II 4.1 Geometria Analítica e as Coordenadas Cartesianas 4.2 Superfícies 4.2.1 Superfícies planas 4.2.2 Superfícies
APLICAÇÕES NA GEOMETRIA ANALÍTICA 4 Gil da Costa Marques TÓPICO Fundamentos da Matemática II 4.1 Geometria Analítica e as Coordenadas Cartesianas 4.2 Superfícies 4.2.1 Superfícies planas 4.2.2 Superfícies
Curso de Geometria Analítica. Hipérbole
 Curso de Geometria Analítica Abrangência: Graduação em Engenharia e Matemática - Professor Responsável: Anastassios H. Kambourakis Resumo Teórico 03 - Cônicas- Circunferência, Elipse, Hipérbole e Parábola
Curso de Geometria Analítica Abrangência: Graduação em Engenharia e Matemática - Professor Responsável: Anastassios H. Kambourakis Resumo Teórico 03 - Cônicas- Circunferência, Elipse, Hipérbole e Parábola
Geometria Analítica. Superfícies. Prof Marcelo Maraschin de Souza
 Geometria Analítica Superfícies Prof Marcelo Maraschin de Souza Superfícies Quadráticas A equação geral do 2º grau nas três variáveis x,y e z ax 2 + by 2 + cz 2 + 2dxy + 2exz + 2fyz + mx + ny + pz + q
Geometria Analítica Superfícies Prof Marcelo Maraschin de Souza Superfícies Quadráticas A equação geral do 2º grau nas três variáveis x,y e z ax 2 + by 2 + cz 2 + 2dxy + 2exz + 2fyz + mx + ny + pz + q
aula Medidas de dispersão: ferramentas úteis na análise estatística Matemática e Realidade Autores 2ª Edição
 2ª Edição DISCIPLINA Matemática e Realidade Medidas de dispersão: ferramentas úteis na análise estatística Autores Ivone da Silva Salsa Jeanete Alves Moreira Marcelo Gomes Pereira aula 10 Governo Federal
2ª Edição DISCIPLINA Matemática e Realidade Medidas de dispersão: ferramentas úteis na análise estatística Autores Ivone da Silva Salsa Jeanete Alves Moreira Marcelo Gomes Pereira aula 10 Governo Federal
Cálculo a Várias Variáveis I - MAT Cronograma para P1: aulas teóricas (segundas e quartas)
 Cálculo a Várias Variáveis I - MAT 116 014.1 Cronograma para P1: aulas teóricas (segundas e quartas) Aula 01 1 de fevereiro (quarta) Aula 0 17 de fevereiro (segunda) Aula 0 19 de fevereiro (quarta) Referências:
Cálculo a Várias Variáveis I - MAT 116 014.1 Cronograma para P1: aulas teóricas (segundas e quartas) Aula 01 1 de fevereiro (quarta) Aula 0 17 de fevereiro (segunda) Aula 0 19 de fevereiro (quarta) Referências:
Derivadas Parciais Capítulo 14
 Derivadas Parciais Capítulo 14 DERIVADAS PARCIAIS Como vimos no Capítulo 4, no Volume I, um dos principais usos da derivada ordinária é na determinação dos valores máximo e mínimo. DERIVADAS PARCIAIS 14.7
Derivadas Parciais Capítulo 14 DERIVADAS PARCIAIS Como vimos no Capítulo 4, no Volume I, um dos principais usos da derivada ordinária é na determinação dos valores máximo e mínimo. DERIVADAS PARCIAIS 14.7
Equações paramétricas das cônicas
 Aula 1 Equações paramétricas das cônicas Ao estudarmos as retas no plano, vimos que a reta r que passa por dois pontos distintos P 1 = x 1, y 1 ) e P = x, y ) é dada pelas seguintes equações paramétricas:
Aula 1 Equações paramétricas das cônicas Ao estudarmos as retas no plano, vimos que a reta r que passa por dois pontos distintos P 1 = x 1, y 1 ) e P = x, y ) é dada pelas seguintes equações paramétricas:
SEÇÕES CÔNICAS. Figura 1
 INSTITUTO DE MATEMÁTICA UFBA DISCIPLINA: MATEMÁTICA BÁSICA II - SEM. 004.1 PROF. GRAÇA LUZIA DOMINGUEZ SANTOS SEÇÕES CÔNICAS Sejam duas retas e e r concorrentes em O, tal que o ângulo α entre e e r é diferente
INSTITUTO DE MATEMÁTICA UFBA DISCIPLINA: MATEMÁTICA BÁSICA II - SEM. 004.1 PROF. GRAÇA LUZIA DOMINGUEZ SANTOS SEÇÕES CÔNICAS Sejam duas retas e e r concorrentes em O, tal que o ângulo α entre e e r é diferente
Geometria Analítica II - Aula 4 82
 Geometria Analítica II - Aula 4 8 IM-UFF K. Frensel - J. Delgado Aula 5 Esferas Iniciaremos o nosso estudo sobre superfícies com a esfera, que já nos é familiar. A esfera S de centro no ponto A e raio
Geometria Analítica II - Aula 4 8 IM-UFF K. Frensel - J. Delgado Aula 5 Esferas Iniciaremos o nosso estudo sobre superfícies com a esfera, que já nos é familiar. A esfera S de centro no ponto A e raio
GGM Geometria Analítica e Cálculo Vetorial Geometria Analítica Básica 20/12/2012- GGM - UFF Dirce Uesu
 GGM0016 Geometria Analítica e Cálculo Vetorial Geometria Analítica Básica 0/1/01- GGM - UFF Dirce Uesu CÔNICAS DEFINIÇÃO GEOMÉTRICA Exercício: Acesse o sitio abaixo e use o programa: http://www.professores.uff.br/hjbortol/disciplinas/005.1/gma04096/applets/conic/co
GGM0016 Geometria Analítica e Cálculo Vetorial Geometria Analítica Básica 0/1/01- GGM - UFF Dirce Uesu CÔNICAS DEFINIÇÃO GEOMÉTRICA Exercício: Acesse o sitio abaixo e use o programa: http://www.professores.uff.br/hjbortol/disciplinas/005.1/gma04096/applets/conic/co
Geometria Analítica. Cônicas. Prof. Vilma Karsburg
 Geometria Analítica Cônicas Prof. Vilma Karsburg Cônicas Sejam duas retas e e g concorrentes em O e não perpendiculares. Considere e fixa e g girar 360 em torno de e, mantendo constante o ângulo entre
Geometria Analítica Cônicas Prof. Vilma Karsburg Cônicas Sejam duas retas e e g concorrentes em O e não perpendiculares. Considere e fixa e g girar 360 em torno de e, mantendo constante o ângulo entre
6. FUNÇÃO QUADRÁTICA 6.1. CONSIDERAÇÕES PRELIMINARES
 47 6. FUNÇÃO QUADRÁTICA 6.1. CONSIDERAÇÕES PRELIMINARES Na figura abaixo, seja a reta r e o ponto F de um determinado plano, tal que F não pertence a r. Consideremos as seguintes questões: Podemos obter,
47 6. FUNÇÃO QUADRÁTICA 6.1. CONSIDERAÇÕES PRELIMINARES Na figura abaixo, seja a reta r e o ponto F de um determinado plano, tal que F não pertence a r. Consideremos as seguintes questões: Podemos obter,
Aula 31 Funções vetoriais de uma variável real
 MÓDULO 3 - AULA 31 Aula 31 Funções vetoriais de uma variável real Objetivos Conhecer as definições básicas de funções vetoriais de uma variável real. Aprender a parametrizar curvas simples. Introdução
MÓDULO 3 - AULA 31 Aula 31 Funções vetoriais de uma variável real Objetivos Conhecer as definições básicas de funções vetoriais de uma variável real. Aprender a parametrizar curvas simples. Introdução
Universidade Federal de Ouro Preto Departamento de Matemática MTM131 - T84 Geometria Analítica e Cálculo Vetorial Cônicas - Tiago de Oliveira
 Universidade Federal de Ouro Preto Departamento de Matemática MTM11 - T8 Geometria Analítica e Cálculo Vetorial Cônicas - Tiago de Oliveira 1. Determine a equação geral da elipse que satisfaça as condições
Universidade Federal de Ouro Preto Departamento de Matemática MTM11 - T8 Geometria Analítica e Cálculo Vetorial Cônicas - Tiago de Oliveira 1. Determine a equação geral da elipse que satisfaça as condições
Descrevendo Regiões no Plano Cartesiano e no Espaço Euclidiano
 Descrevendo Regiões no Plano Cartesiano e no Espaço Euclidiano Americo Cunha Débora Mondaini Ricardo Sá Earp Departamento de Matemática Pontifícia Universidade Católica do Rio de Janeiro Regiões no Plano
Descrevendo Regiões no Plano Cartesiano e no Espaço Euclidiano Americo Cunha Débora Mondaini Ricardo Sá Earp Departamento de Matemática Pontifícia Universidade Católica do Rio de Janeiro Regiões no Plano
aula Vetores no plano e no espaço tridimensional Geometria Analítica e Números Complexos Autores Cláudio Carlos Dias Neuza Maria Dantas
 D I S C I P L I N A Geometria Analítica e Números Compleos Vetores no plano e no espaço tridimensional Autores Cláudio Carlos Dias Neuza Maria Dantas aula 10 Goerno Federal Presidente da República Luiz
D I S C I P L I N A Geometria Analítica e Números Compleos Vetores no plano e no espaço tridimensional Autores Cláudio Carlos Dias Neuza Maria Dantas aula 10 Goerno Federal Presidente da República Luiz
MÓDULO 1 - AULA 21. Objetivos
 Aula 1 Hipérbole - continuação Objetivos Aprender a desenhar a hipérbole com compasso e régua com escala. Determinar a equação reduzida da hipérbole no sistema de coordenadas com origem no ponto médio
Aula 1 Hipérbole - continuação Objetivos Aprender a desenhar a hipérbole com compasso e régua com escala. Determinar a equação reduzida da hipérbole no sistema de coordenadas com origem no ponto médio
Porque?
 Porque? 6 Parábola Dados um ponto F e uma reta d, com F d, seja p = d(f,d). Chamamos parábola o conjunto dos pontos P do plano que são equidistantes de F e d, i. é., d(p,f)= d(p,d). 7 Elementos da Parábola
Porque? 6 Parábola Dados um ponto F e uma reta d, com F d, seja p = d(f,d). Chamamos parábola o conjunto dos pontos P do plano que são equidistantes de F e d, i. é., d(p,f)= d(p,d). 7 Elementos da Parábola
Objetivos. Aprender a propriedade reflexiva da parábola.
 Aula 16 Parábola - continuação MÓDULO 1 - AULA 16 Objetivos Descrever a parábola como um lugar geométrico, determinando a sua equação reduzida nos sistemas de coordenadas com eixo y paralelo à diretriz
Aula 16 Parábola - continuação MÓDULO 1 - AULA 16 Objetivos Descrever a parábola como um lugar geométrico, determinando a sua equação reduzida nos sistemas de coordenadas com eixo y paralelo à diretriz
Notas de Aulas 3 - Cônicas Prof Carlos A S Soares
 Notas de Aulas 3 - Cônicas Prof Carlos A S Soares 1 Parábolas 11 Conceito e Elementos Definição 1 Sejam l uma reta e F um ponto não pertencente a l Chamamos parábola de diretriz l e foco F o conjunto dos
Notas de Aulas 3 - Cônicas Prof Carlos A S Soares 1 Parábolas 11 Conceito e Elementos Definição 1 Sejam l uma reta e F um ponto não pertencente a l Chamamos parábola de diretriz l e foco F o conjunto dos
INSTITUTO FEDERAL DE BRASILIA 4ª Lista. Nome: DATA: 09/11/2016
 INSTITUTO FEDERAL DE BRASILIA 4ª Lista MATEMÁTICA GEOMETRIA ANALÍTICA Nome: DATA: 09/11/016 Alexandre Uma elipse tem centro na origem e o eixo maior coincide com o eixo Y. Um dos focos é 1 F1 0, 3 e a
INSTITUTO FEDERAL DE BRASILIA 4ª Lista MATEMÁTICA GEOMETRIA ANALÍTICA Nome: DATA: 09/11/016 Alexandre Uma elipse tem centro na origem e o eixo maior coincide com o eixo Y. Um dos focos é 1 F1 0, 3 e a
aula O ensino utilizando projetos em ciência, tecnologia e sociedade Instrumentação para o Ensino de Química I Autores Luiz Seixas das Neves
 D I S C I P L I N A Instrumentação para o Ensino de Química I O ensino utilizando projetos em ciência, tecnologia e sociedade Autores Luiz Seixas das Neves Márcia Gorette Lima da Silva aula 15 Governo
D I S C I P L I N A Instrumentação para o Ensino de Química I O ensino utilizando projetos em ciência, tecnologia e sociedade Autores Luiz Seixas das Neves Márcia Gorette Lima da Silva aula 15 Governo
Instituto de Matemática UFBA Disciplina: Geometria Analítica Mat A01 Última Atualização ª lista - Cônicas
 Instituto de Matemática UFBA Disciplina: Geometria Analítica Mat A01 Última Atualização - 005 1ª lista - Cônicas 1 0 ) Em cada um dos seguintes itens, determine uma equação da parábola a partir dos elementos
Instituto de Matemática UFBA Disciplina: Geometria Analítica Mat A01 Última Atualização - 005 1ª lista - Cônicas 1 0 ) Em cada um dos seguintes itens, determine uma equação da parábola a partir dos elementos
Aula 4. Coordenadas polares. Definição 1. Observação 1
 Aula Coordenadas polares Nesta aula veremos que há outra maneira de expressar a posição de um ponto no plano, distinta da forma cartesiana Embora os sistemas cartesianos sejam muito utilizados, há curvas
Aula Coordenadas polares Nesta aula veremos que há outra maneira de expressar a posição de um ponto no plano, distinta da forma cartesiana Embora os sistemas cartesianos sejam muito utilizados, há curvas
1 Cônicas Não Degeneradas
 Seções Cônicas Reginaldo J. Santos Departamento de Matemática-ICE Universidade Federal de Minas Gerais http://www.mat.ufmg.br/~regi regi@mat.ufmg.br 11 de dezembro de 2001 Estudaremos as (seções) cônicas,
Seções Cônicas Reginaldo J. Santos Departamento de Matemática-ICE Universidade Federal de Minas Gerais http://www.mat.ufmg.br/~regi regi@mat.ufmg.br 11 de dezembro de 2001 Estudaremos as (seções) cônicas,
Distância entre duas retas. Regiões no plano
 Capítulo 4 Distância entre duas retas. Regiões no plano Nesta aula, veremos primeiro como podemos determinar a distância entre duas retas paralelas no plano. Para isso, lembramos que, na aula anterior,
Capítulo 4 Distância entre duas retas. Regiões no plano Nesta aula, veremos primeiro como podemos determinar a distância entre duas retas paralelas no plano. Para isso, lembramos que, na aula anterior,
Aula 14 Círculo. Objetivos
 Aula 1 Círculo MÓDULO 1 - AULA 1 Objetivos Determinar a equação do círculo de centro C e raio r, como um lugar geométrico. Aprender os conceitos de retas tangente e normal num ponto P de um círculo. Esboçar
Aula 1 Círculo MÓDULO 1 - AULA 1 Objetivos Determinar a equação do círculo de centro C e raio r, como um lugar geométrico. Aprender os conceitos de retas tangente e normal num ponto P de um círculo. Esboçar
Lista de Exercícios de Cálculo 3 Módulo 1 - Terceira Lista - 02/2016
 Lista de Exercícios de Cálculo 3 Módulo 1 - Terceira Lista - 02/2016 Parte A 1. Identifique e esboce as superfícies quádricas x 2 + 4y 2 + 9z 2 = 1 x 2 y 2 + z 2 = 1 (c) y = 2x 2 + z 2 (d) x = y 2 z 2
Lista de Exercícios de Cálculo 3 Módulo 1 - Terceira Lista - 02/2016 Parte A 1. Identifique e esboce as superfícies quádricas x 2 + 4y 2 + 9z 2 = 1 x 2 y 2 + z 2 = 1 (c) y = 2x 2 + z 2 (d) x = y 2 z 2
Matemática I Cálculo I Unidade B - Cônicas. Profª Msc. Débora Bastos. IFRS Campus Rio Grande FURG UNIVERSIDADE FEDERAL DO RIO GRANDE
 Unidade B - Cônicas Profª Msc. Débora Bastos IFRS Campus Rio Grande FURG UNIVERSIDADE FEDERAL DO RIO GRANDE 22 12. Cônicas São chamadas cônicas as curvas resultantes do corte de um cone duplo com um plano.
Unidade B - Cônicas Profª Msc. Débora Bastos IFRS Campus Rio Grande FURG UNIVERSIDADE FEDERAL DO RIO GRANDE 22 12. Cônicas São chamadas cônicas as curvas resultantes do corte de um cone duplo com um plano.
6.1 equações canônicas de círculos e esferas
 6 C Í R C U LO S E E S F E R A S 6.1 equações canônicas de círculos e esferas Um círculo é o conjunto de pontos no plano que estão a uma certa distância r de um ponto dado (a, b). Desta forma temos que
6 C Í R C U LO S E E S F E R A S 6.1 equações canônicas de círculos e esferas Um círculo é o conjunto de pontos no plano que estão a uma certa distância r de um ponto dado (a, b). Desta forma temos que
3. Achar a equação da esfera definida pelas seguintes condições: centro C( 4, 2, 3) e tangente ao plano π : x y 2z + 7 = 0.
 Universidade Federal de Uerlândia Faculdade de Matemática Disciplina : Geometria Analítica (GMA00) Assunto: Superfícies, Quádricas, Curvas e Coordenadas Professor Sato 4 a Lista de exercícios. Determinar
Universidade Federal de Uerlândia Faculdade de Matemática Disciplina : Geometria Analítica (GMA00) Assunto: Superfícies, Quádricas, Curvas e Coordenadas Professor Sato 4 a Lista de exercícios. Determinar
Este trabalho foi licenciado com a Licença Creative Commons Atribuição - NãoComercial - SemDerivados 3.0 Não Adaptada
 1. Introdução Definição: Parábola é o lugar geométrico dos pontos do plano cujas distâncias entre uma reta fixa, chamada de reta diretriz, e a um ponto fixo situado fora desta reta, chamado de foco da
1. Introdução Definição: Parábola é o lugar geométrico dos pontos do plano cujas distâncias entre uma reta fixa, chamada de reta diretriz, e a um ponto fixo situado fora desta reta, chamado de foco da
9º ANO FUNÇÕES. Função Quadrática. Nuno Marreiros
 Nuno Marreiros 9º ANO FUNÇÕES Função Quadrática Ponto de partida Já foi estudada a função de proporcionalidade direta bem como a função de proporcionalidade inversa. Hoje vamos aprender e estudar um pouco
Nuno Marreiros 9º ANO FUNÇÕES Função Quadrática Ponto de partida Já foi estudada a função de proporcionalidade direta bem como a função de proporcionalidade inversa. Hoje vamos aprender e estudar um pouco
CÔNICAS E QUÁDRICAS. Álgebra Linear e Geometria Analítica Prof. Aline Paliga
 CÔNICAS E QUÁDRICAS Álgebra Linear e Geometria Analítica Prof. Aline Paliga 11.1 CÔNICAS Pierre de Fermat (1601-1665) estabeleceu o princípio fundamental da Geometria Analítica, segundo o qual, uma equação
CÔNICAS E QUÁDRICAS Álgebra Linear e Geometria Analítica Prof. Aline Paliga 11.1 CÔNICAS Pierre de Fermat (1601-1665) estabeleceu o princípio fundamental da Geometria Analítica, segundo o qual, uma equação
Geometria Analítica: Cônicas
 Geometria Analítica: Cônicas 1 Geometria Analítica: Cônicas 1. Parábola Definição: Considere em um plano uma reta d e um ponto F não pertencente à d. Parábola é o lugar geométrico formado pelo conjunto
Geometria Analítica: Cônicas 1 Geometria Analítica: Cônicas 1. Parábola Definição: Considere em um plano uma reta d e um ponto F não pertencente à d. Parábola é o lugar geométrico formado pelo conjunto
Matemática. Resolução das atividades complementares. M21 Geometria Analítica: Cônicas
 Resolução das atividades complementares Matemática M Geometria Analítica: Cônicas p. FGV-SP) Determine a equação da elipse de centro na origem que passa pelos pontos A, 0), B, 0) e C0, ). O centro da elipse
Resolução das atividades complementares Matemática M Geometria Analítica: Cônicas p. FGV-SP) Determine a equação da elipse de centro na origem que passa pelos pontos A, 0), B, 0) e C0, ). O centro da elipse
0 < c < a ; d(f 1, F 2 ) = 2c
 Capítulo 14 Elipse Nosso objetivo, neste e nos próximos capítulos, é estudar a equação geral do segundo grau em duas variáveis: Ax + Bxy + Cy + Dx + Ey + F = 0, onde A 0 ou B 0 ou C 0 Para isso, deniremos,
Capítulo 14 Elipse Nosso objetivo, neste e nos próximos capítulos, é estudar a equação geral do segundo grau em duas variáveis: Ax + Bxy + Cy + Dx + Ey + F = 0, onde A 0 ou B 0 ou C 0 Para isso, deniremos,
Exercícios Resolvidos Esboço e Análise de Conjuntos
 Instituto uperior Técnico Departamento de Matemática ecção de Álgebra e Análise Eercícios Resolvidos Esboço e Análise de Conjuntos Eercício Esboce detalhadamente o conjunto descrito por = {(,, ) R 3 :,,
Instituto uperior Técnico Departamento de Matemática ecção de Álgebra e Análise Eercícios Resolvidos Esboço e Análise de Conjuntos Eercício Esboce detalhadamente o conjunto descrito por = {(,, ) R 3 :,,
Universidade Federal de Mato Grosso do Sul - UFMS VGA - 2 a Prova - Engenharia Civil + Física 03 de Julho de Prof o. E.T.
 Universidade Federal de Mato Grosso do Sul - UFMS VGA - 2 a Prova - Engenharia Civil + Física 0 de Julho de 2014 - Prof o ETGalante 1 (2,0 pontos) Na gura acima ABCDEF GH é um paralelepípedo O ponto M
Universidade Federal de Mato Grosso do Sul - UFMS VGA - 2 a Prova - Engenharia Civil + Física 0 de Julho de 2014 - Prof o ETGalante 1 (2,0 pontos) Na gura acima ABCDEF GH é um paralelepípedo O ponto M
Aula 15 Parábola. Objetivos
 MÓDULO 1 - AULA 15 Aula 15 Parábola Objetivos Descrever a parábola como um lugar geométrico determinando a sua equação reduzida nos sistemas de coordenadas com eixo x paralelo à diretriz l e origem no
MÓDULO 1 - AULA 15 Aula 15 Parábola Objetivos Descrever a parábola como um lugar geométrico determinando a sua equação reduzida nos sistemas de coordenadas com eixo x paralelo à diretriz l e origem no
MAT Poli Cônicas - Parte II
 MAT2454 - Poli - 2011 Cônicas - Parte II Neste texto apresentamos definições de elipse, hipérbole e parábola e deduzimos suas equações reduzidas. Nos exercícios são apresentadas as propriedades ópticas
MAT2454 - Poli - 2011 Cônicas - Parte II Neste texto apresentamos definições de elipse, hipérbole e parábola e deduzimos suas equações reduzidas. Nos exercícios são apresentadas as propriedades ópticas
Capítulo 12. Ângulo entre duas retas no espaço. Definição 1. O ângulo (r1, r2 ) entre duas retas r1 e r2 é assim definido:
 Capítulo 1 1. Ângulo entre duas retas no espaço Definição 1 O ângulo (r1, r ) entre duas retas r1 e r é assim definido: (r1, r ) 0o se r1 e r são coincidentes, se as retas são concorrentes, isto é, r1
Capítulo 1 1. Ângulo entre duas retas no espaço Definição 1 O ângulo (r1, r ) entre duas retas r1 e r é assim definido: (r1, r ) 0o se r1 e r são coincidentes, se as retas são concorrentes, isto é, r1
Didática D I S C I P L I N A. Elaboração de um plano de ensino I. Autores. André Ferrer Pinto Martins. Iran Abreu Mendes. aula
 D I S C I P L I N A Didática Elaboração de um plano de ensino I Autores André Ferrer Pinto Martins Iran Abreu Mendes aula 13 Governo Federal Presidente da República Luiz Inácio Lula da Silva Ministro da
D I S C I P L I N A Didática Elaboração de um plano de ensino I Autores André Ferrer Pinto Martins Iran Abreu Mendes aula 13 Governo Federal Presidente da República Luiz Inácio Lula da Silva Ministro da
APLICAÇÕES DE CÔNICAS NA ENGENHARIA
 O que você deve saber sobre APLICAÇÕES DE CÔNICAS NA ENGENHARIA As equações das curvas chamadas cônicas recebem esse nome devido à sua origem (a intersecção de um cone por um plano) e podem ser determinadas
O que você deve saber sobre APLICAÇÕES DE CÔNICAS NA ENGENHARIA As equações das curvas chamadas cônicas recebem esse nome devido à sua origem (a intersecção de um cone por um plano) e podem ser determinadas
1. A partir da definição, determinar a equação da parábola P, cujo foco é F = (3, 4) e cuja diretriz é L : x + y 2 = 0. (x 3) 2 + (y + 4) 2 =
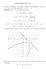 QUESTÕES-AULA 18 1. A partir da definição, determinar a equação da parábola P, cujo foco é F = (3, 4) e cuja diretriz é L : x + y = 0. Solução Seja P = (x, y) R. Temos que P P d(p, F ) = d(p, L) (x 3)
QUESTÕES-AULA 18 1. A partir da definição, determinar a equação da parábola P, cujo foco é F = (3, 4) e cuja diretriz é L : x + y = 0. Solução Seja P = (x, y) R. Temos que P P d(p, F ) = d(p, L) (x 3)
Matéria das Aulas e Exercícios Recomendados Cálculo II- MAA
 Matéria das Aulas e Exercícios Recomendados Cálculo II- MAA Número da Aula Data da Aula 1 02/09 Sequências Numéricas, definição, exemplos, representação geométrica, convergência e divergência, propriedades,
Matéria das Aulas e Exercícios Recomendados Cálculo II- MAA Número da Aula Data da Aula 1 02/09 Sequências Numéricas, definição, exemplos, representação geométrica, convergência e divergência, propriedades,
INSTITUTO FEDERAL DE EDUCAÇÃO, CIÊNCIA E tecnologia PARAÍBA. Ministério da Educação
 INSTITUTO FEDERAL DE EDUCAÇÃO, CIÊNCIA E tecnologia PARAÍBA Ministério da Educação Instituto Federal de Educação, Ciência e Tecnologia da Paraíba - Campus Cajazeiras Diretoria de Ensino / Coord. do Curso
INSTITUTO FEDERAL DE EDUCAÇÃO, CIÊNCIA E tecnologia PARAÍBA Ministério da Educação Instituto Federal de Educação, Ciência e Tecnologia da Paraíba - Campus Cajazeiras Diretoria de Ensino / Coord. do Curso
Elevando ambos os membros desta equação ao quadrado e simplificando o resultado, obtemos, finalmente, Exercícios
 Cónicas 61 Elevando ambos os membros desta equação ao quadrado e simplificando o resultado, obtemos, finalmente, que não contém radicais e é do segundo grau. 40x 2 + 33y 2-24xy + 168x - 168j - 200 = 0,
Cónicas 61 Elevando ambos os membros desta equação ao quadrado e simplificando o resultado, obtemos, finalmente, que não contém radicais e é do segundo grau. 40x 2 + 33y 2-24xy + 168x - 168j - 200 = 0,
Aula Elipse. Definição 1. Nosso objetivo agora é estudar a equação geral do segundo grau em duas variáveis:
 Aula 18 Nosso objetivo agora é estudar a equação geral do segundo grau em duas variáveis: Ax + Bxy + Cy + Dx + Ey + F = 0, onde A 0 ou B 0 ou C 0 Vamos considerar primeiro os casos em que B = 0. Isto é,
Aula 18 Nosso objetivo agora é estudar a equação geral do segundo grau em duas variáveis: Ax + Bxy + Cy + Dx + Ey + F = 0, onde A 0 ou B 0 ou C 0 Vamos considerar primeiro os casos em que B = 0. Isto é,
Vetores e Geometria Analítica
 Vetores e Geometria Analítica ECT2102 Prof. Ronaldo Carlotto Batista 4 de maio de 2016 Círculo Denição Círculo é o conjunto de pontos P (x, y) a uma distância a, chamada de raio, de um ponto C (x o, y
Vetores e Geometria Analítica ECT2102 Prof. Ronaldo Carlotto Batista 4 de maio de 2016 Círculo Denição Círculo é o conjunto de pontos P (x, y) a uma distância a, chamada de raio, de um ponto C (x o, y
7. Determine a equação da parábola que passa pelos pontos P (0, 6), Q(3, 0) e R(4, 10).
 Lista 3: Cônicas - Engenharia Mecânica Professora Elisandra Bär de Figueiredo 1. Determine a equação do conjunto de pontos P (x, y) que são equidistantes da reta x = e do ponto (0, ). A seguir construa
Lista 3: Cônicas - Engenharia Mecânica Professora Elisandra Bär de Figueiredo 1. Determine a equação do conjunto de pontos P (x, y) que são equidistantes da reta x = e do ponto (0, ). A seguir construa
REVISÃO. aula. Natureza ondulatória da matéria. Arquitetura Atômica e Molecular. Autores. Ótom Anselmo de Oliveira. Joana D Arc Gomes Fernandes
 D I S C I P L I N A Arquitetura Atômica e Molecular Material APROVADO (conteúdo e imagens) Data : / / Nome: Natureza ondulatória da matéria Autores Ótom Anselmo de Oliveira Joana D Arc Gomes Fernandes
D I S C I P L I N A Arquitetura Atômica e Molecular Material APROVADO (conteúdo e imagens) Data : / / Nome: Natureza ondulatória da matéria Autores Ótom Anselmo de Oliveira Joana D Arc Gomes Fernandes
Geometria Analítica - Aula
 Geometria Analítica - Aula 18 228 IM-UFF K. Frensel - J. Delgado Aula 19 Continuamos com o nosso estudo da equação Ax 2 + Cy 2 + Dx + Ey + F = 0 1. Hipérbole Definição 1 Uma hipérbole, H, de focos F 1
Geometria Analítica - Aula 18 228 IM-UFF K. Frensel - J. Delgado Aula 19 Continuamos com o nosso estudo da equação Ax 2 + Cy 2 + Dx + Ey + F = 0 1. Hipérbole Definição 1 Uma hipérbole, H, de focos F 1
Capítulo 19. Coordenadas polares
 Capítulo 19 Coordenadas polares Neste capítulo, veremos que há outra maneira de expressar a posição de um ponto no plano, distinta da forma cartesiana. Embora os sistemas cartesianos sejam muito utilizados,
Capítulo 19 Coordenadas polares Neste capítulo, veremos que há outra maneira de expressar a posição de um ponto no plano, distinta da forma cartesiana. Embora os sistemas cartesianos sejam muito utilizados,
Exercícios de Geometria Analítica - CM045
 Exercícios de Geometria Analítica - CM045 Prof. José Carlos Corrêa Eidam DMAT/UFPR Disponível no sítio people.ufpr.br/ eidam/index.htm 1o. semestre de 2011 Parte 1 Soma e produto escalar 1. Seja OABC um
Exercícios de Geometria Analítica - CM045 Prof. José Carlos Corrêa Eidam DMAT/UFPR Disponível no sítio people.ufpr.br/ eidam/index.htm 1o. semestre de 2011 Parte 1 Soma e produto escalar 1. Seja OABC um
C U R S O T É C N I C O E M S E G U R A N Ç A D O T R A B A L H O. matemática. Calculando volume de sólidos geométricos. Elizabete Alves de Freitas
 C U R S O T É C N I C O E M S E G U R A N Ç A D O T R A B A L H O 06 matemática Calculando volume de sólidos geométricos Elizabete Alves de Freitas Governo Federal Ministério da Educação Projeto Gráfico
C U R S O T É C N I C O E M S E G U R A N Ç A D O T R A B A L H O 06 matemática Calculando volume de sólidos geométricos Elizabete Alves de Freitas Governo Federal Ministério da Educação Projeto Gráfico
SISTEMA DE EIXOS COORDENADOS
 PET FÍSICA SISTEMA DE EIXOS COORDENADOS Aula 6 TATIANA MIRANDA DE SOUZA VICTOR ABATH DA SILVA FREDERICO ALAN DE OLIVEIRA CRUZ AGRADECIMENTOS Esse material foi produzido com apoio do Fundo Nacional de Desenvolvimento
PET FÍSICA SISTEMA DE EIXOS COORDENADOS Aula 6 TATIANA MIRANDA DE SOUZA VICTOR ABATH DA SILVA FREDERICO ALAN DE OLIVEIRA CRUZ AGRADECIMENTOS Esse material foi produzido com apoio do Fundo Nacional de Desenvolvimento
Universidade Federal de Mato Grosso do Sul - UFMS VGA - 2 a Prova - Engenharia de Computação 03 de Julho de Prof o. E.T.
 Universidade Federal de Mato Grosso do Sul - UFMS VGA - 2 a Prova - Engenharia de Computação 0 de Julho de 2014 - Prof o ETGalante 1 (2,0 pontos) Na gura acima ABCDEF GH é um paralelepípedo O ponto M é
Universidade Federal de Mato Grosso do Sul - UFMS VGA - 2 a Prova - Engenharia de Computação 0 de Julho de 2014 - Prof o ETGalante 1 (2,0 pontos) Na gura acima ABCDEF GH é um paralelepípedo O ponto M é
Resumo: Nestas notas faremos um breve estudo sobre as principais propriedades. mínimos, gráficos e algumas aplicações simples.
 Universidade Estadual de Maringá - Departamento de Matemática Cálculo Diferencial e Integral: um KIT de Sobrevivência c Publicação Eletrônica do KIT http://www.dma.uem.br/kit Equação quadrática Prof. Doherty
Universidade Estadual de Maringá - Departamento de Matemática Cálculo Diferencial e Integral: um KIT de Sobrevivência c Publicação Eletrônica do KIT http://www.dma.uem.br/kit Equação quadrática Prof. Doherty
FICHA de AVALIAÇÃO de MATEMÁTICA A 10.º Ano Versão 4
 FICHA de AVALIAÇÃO de MATEMÁTICA A 0.º Ano Versão Nome: N.º Turma: Apresente o seu raciocínio de forma clara, indicando todos os cálculos que tiver de efetuar e todas as justificações necessárias. Quando,
FICHA de AVALIAÇÃO de MATEMÁTICA A 0.º Ano Versão Nome: N.º Turma: Apresente o seu raciocínio de forma clara, indicando todos os cálculos que tiver de efetuar e todas as justificações necessárias. Quando,
