Os únicos candidatos a extremantes locais são os pontos críticos de f pois o D f 2 é aberto. f
|
|
|
- Iasmin de Almeida Tomé
- 6 Há anos
- Visualizações:
Transcrição
1 CAPÍTULO 16 Exercícios 16 1 Seja (x y) x y xy x y Os únicos candidatos a extremantes locais são os pontos críticos de pois o D é aberto De ( x x y ) x y ( y x y ) y x 1 resulta que os candidatos a extremantes locais são as soluções do sistema: { xy0 yx1 0 A solução do sistema é 0 1 Temos e 0 1 x y 0 Portanto (x y) x 3 y xy 5 ( x x y ) 3x y y ( x y) y x é candidato a ponto de mínimo local Resolvendo o sistema Ï3x y0 Óyx0 encontramos os pontos críticos (0 0) e Agora ( x y) 6x x x ( 0 0)00 e x ; 6 1 ( x y) y y ( 0 0) 0 e y
2 1 1 O ponto 6 1 é candidato a ponto de máximo local Seja g(x) (x 0) x 3 5 O ponto x 0 não é extremante local de g(x) Portanto o ponto (0 0) não é extremante local de (x y) 6 (x y) x 5 y 5 5x 5y ( x x y ) 5x 5 y ( x y) 5y 5 Resolvendo o sistema: Ï5x 50 x1 5y Ó 50 y 1 Os pontos (1 1) (1 1) (1 1) (1 1) são pontos críticos Temos: 3 ( x y) 0 x ( 1 1) 0 0 e ( 1 1) 0 0; x x x 3 ( x y) 0 y ( 1 1) 0 0 e ( 1 1) 0 0 y y y O ponto (1 1) é candidato a mínimo local e o ponto (1 1) máximo local Agora: x ( 1 1) 0 0 e x ( 11 ) 00; y ( 1 1) 0 0 e y ( 11 ) 00 Os pontos (1 1) e (1 1) não são extremantes locais Exercícios a) (x y) x 3xy y 6x y ( x x y ) x 3y 6 y ( x y) 8y 3x 10
3 Resolvendo o sistema: Ïx3y6 Ó3x8y Ponto crítico: Hessiano de : H (x y) ( x y) ( x xy x y ) xy x y ( ) ( x y) y H e 5 5 x Logo 7 7 mínimo local de e também mínimo global (conorme Exercício ) c) (x y) x 3 xy y 5x x (x y) 3x y 5 é ponto de y (x y) y x Resolvendo o sistema: Ï3x y 5 Óyx 0 Pontos críticos: (1 1) e Hessiano de : H (x y) ( x y) ( x xy x y ) 6x 1x xy x y ( ) ( x y) y H(1 1) 16 0 então (1 1) é ponto de sela H e x
4 Logo é ponto de mínimo local (Não é mínimo global pois g(x) (x 0) x 3 5 x e (x 0) para x ) e) (x y) x 3 3x y 7y x (x y) 3x 6xy y (x y) 3x 7 Resolvendo o sistema Ï3x 6xy0 3x Ó 70 encontramos: e 3 Hessiano de : H (x y) ( x y) ( x xy x y ) 6x6y 6x 6 0 xy x y x ( ) ( x y) y H H Logo e 3 são pontos de sela Seja P (0 0 0) e P 1 (x y x y 1 3 ) z Distância entre os pontos P e P 1 : d (P P 1 ) x y ( xy) Vamos minimizar (x y) x y (x y ) 1
5 x y (x y) x (x y ) (x y) y (x y ) Resolvendo o sistema: xy8 { obtemos x10y16 x y z 3 ; e 3 3 H(x y) 0 e 10 x mínimo global de (x y) 0 Logo é ponto de Assim P é o ponto procurado 7 a) Seja (x) x e E ( )  [(a i ) b i ] i 1 Consideremos: a i b i a i a i b i E ( ) E a  i 1  [a i b i ] i 1 a i (a i b i ) E  (a i b i ) i 1 13
6 13 Temos o sistema: Ï a  i b  ai  aibi i 1 i 1 i 1 Âai b  bi Ó i1 i1 Logo Ï6 387 Ó Daí e 10 1 A reta que melhor se ajusta aos dados observados é y x 10 b) Se x 10 então y L(x y) x(10 x) y(00 y) (x y xy) L(x y) 3x 3y xy 10x 00y Para maximizar o lucro: L x (x y) 6x y 10 Þ 3x y 60 Þ x 10 e y 30 L (x y) 6y x 00 Þ 3y x 100 x L Á ( x y) 6 0 e H(x y) x Logo a produção que maximiza o lucro é x 10 e y Sejam P (x y 1 3x y) plano (0 0 0) Q (1 1 1) Distância entre os pontos: d(p O) x y ( 1 3xy) e d(p Q) ( x1) ( y1) ( 113xy) 1
7 Devemos minimizar a unção: g(x y) x y (1 3x y) (x 1) (y 1) (11 3x y) g(x y) 0x 10y xy 10x 9y 67 g (x y) 0x y 10 x g (x y) 0y x 9 y Resolvendo o sistema: Ï0xy10 Ó0yx9 3 5 temos x y z 1 16 e H(x y) 0 g 3 (x y) 0 Logo x 0 x 1 global de g 5 e y é ponto de mínimo 1 Portanto P Seja (x y) 1 x y x 0 e y 0 Plano tangente ao gráico de z z 0 x (x 0 y 0 ) (x x 0 ) y (x 0 y 0 ) (y y 0 ) ou seja z 1 x0 y0 x 0 (x x 0 ) y 0 (y y 0 ) Daí z x 0 x y 0 y x 0 y 0 1 A seguir vamos determinar o volume do tetraedro determinado pelo plano tangente e pelos planos coordenados Temos x 0 e y 0 Þ z x0 y0 1 x y x 0 e z 0 Þ y e y0 x y y 0 e z 0 Þ x x0 Da Geometria Analítica sabemos que o volume do tetraedro é 1 6 paralelepípedo Portanto do volume do V 1 6 ( x0 y0 1) 3 ( x y ) 3 x0y0 x0y0 15
8 Devemos minimizar a unção volume: V(x y) ( x y 1 ) 3 xy V x ( x y 1) ( 5x y 1) ( x y) e xy V y x y ( x y 1) ( 5y x 1) ( ) xy Resolvendo o sistema Ï5x y 1 5y x Ó 1 temos x 1 e y 1 Mas x 0 e y 0 portanto (x 0 y 0 z 0 ) Equação do plano tangente que orma com os planos coordenados um tetraedro de volume mínimo: z x 0 x y 0 y x0 y0 1 ou seja z x y 3 0 Não pois (0 0) é o único ponto crítico de (x y) x (1 y) 3 y é ponto de mínimo local mas não é ponto de mínimo global (Observação Esta unção oi sugerida pelo Proessor Luiz Augusto Fernandes do IME-USP) Exercícios 16 1 d) Seja (x y) xy em A {(x y) e x 0 y 0 e x y 5} O teorema de Weierstrass garante que assume em A valor máximo e valor mínimo pois é contínua e A é compacto x ( x y) y e y ( x y) x O único ponto crítico é (0 0) que não pertence ao interior de A 16
9 Portanto os valores máximo e mínimo de em A são atingidos na ronteira de A Análise dos pontos de ronteira: (x 0) 0 em 0 x 5 (0 y) 0 em 0 y 5 g(x) (x 5 x) x(5 x) 5x x 5 5 g'(x) 5 x Daí 5 x 0 Þ x Þ y5x g"(x) Concluímos que: O valor mínimo é 0 e é atingido nos pontos (x 0) 0 x 5 (0 y) 0 y 5 e nos pontos O valor máximo é 5 8 atingido em 5 5 ) Seja (x y) x xy y em A {(x y) / x y 1} Como é contínua e A compacto assume em A valor máximo e valor mínimo (teorema de Weierstrass) x ( xy ) xy y ( xy ) y x (0 0) é o único ponto crítico x (0 0) 0 e H (0 0) 8 0 Logo (0 0) 0 é valor mínimo global de (Veja Exercício Seção 163) 17
10 Vamos analisar agora o que ocorre na ronteira Sobre o segmento de extremidades (0 1) e (1 0) os valores de são dados por g(x) (x 1 x) ou seja g(x) 5x 6x com 0 x 1 cujo gráico é um arco de parábola com concavidade para cima logo sobre este lado o valor máximo deverá ocorrer em uma das extremidades (ou em ambas) De g(1) 1 e g(0) segue que sobre este lado o valor máximo é e ocorre em (0 1) De orma análoga conclui-se que sobre os outros lados o valor máximo deverá ocorrer também nos vértices Calculando os valores de nos vértices: (1 0) 1; (0 1) ; (1 0) 1 e (0 1) O valor máximo é sendo atingido nos pontos (0 1) e (0 1) 3 Seja T(x y) x y e A {(x y) x 0 y x e y x } Como T é uma unção contínua e A compacto então T assume em A valor máximo e valor mínimo Temos T (x y) x e (0 0) é o único ponto crítico Temos x T (x y) 0 e H (0 0) 0 logo (0 0) x T (x y) y é um ponto de temperatura máxima em A y E mais T(0 0) é a temperatura máxima Vamos analisar o comportamento da unção na ronteira de A: No segmento OM (y x e 0 x 3 ) F(x) T(x x) x F '(x) x O ponto (0 0) é de máximo e T(0 0) A unção é decrescente em 0 x 3 e T 3 (no vértice M) 3 9 No segmento MN (x 0 y x e y x ): F(x) T(x x ) 1 (5x 8x) F '(x) 1 (10x 8) Þ 10x 8 0 Þ x F "(x) Þ y 8 5 é ponto de máximo no segmento MN
11 T No segmento ON (x 0 e 0 y ) F(y) T(0 y) y F'(y) 8y (0 0) dá temperatura máxima igual a A unção F'(y) é sempre negativa em 0 y Portanto a unção F é estritamente decrescente em 0 y com valor máximo em (0 0) e valor mínimo em (0 ) Logo T(0 ) 0 é a menor temperatura e P (0 ) é o ponto de menor temperatura Exercícios a) Sejam (x y) 3x y e g(x y) x y 1 Vamos achar os extremantes de em B {(x y) g(x y) 0} pelo método dos multiplicadores de Lagrange Como g é de classe C 1 e g(x y) (x y) (0 0) em B temos que os candidatos a extremantes locais são os (x y) que tornam compatível o sistema: Ï ( x y) l g( x y) Ógx ( y) Como l π 0 temos x y l e l Substituindo em x y 1 segue: Þ Ï ( 31) l ( x y) Þ Ó x y Þ 16l 38 Þ l l 16 l Logo os candidatos a extremantes locais são: Á e Á 19 Como B é compacto e Á Á é ponto de máximo e Á 38 Ïlx 3 ly 1 x y Ó Á resulta que d) Sejam (x y) x y e g(x y) xy 1 x 0 e y 0 Vamos encontrar os extremantes de em: é ponto de mínimo B {(x y) g(x y) 0 x 0 e y 0} utilizando o método dos multiplicadores de Lagrange Como g é de classe C 1 e g(x y) (y x) (0 0) em B resulta que os extremantes possíveis são os (x y) que tornam compatível o sistema Ï ( x y) l g( x y) Óg( x y) 0 Þ Ï ( x 8y) l( y x) Ó xy 10 19
12 Resolvendo o sistema l ; x e y O único candidato é Á e veriica-se por inspeção que é um ponto de mínimo (O valor da unção sobre a restrição é dada por g(x) 1 x x ou seja g(x) x x x 0 cuja concavidade é voltada para cima logo para x o valor de g é mínimo Outro modo Como as curvas de nível de são elipses com centros na origem o valor de aumenta à medida que se aasta da origem então o menor valor de sobre a restrição xy 1 x 0 e y 0 deverá ocorrer no ponto em que a curva de nível de tangencia a hipérbole) j) Sejam (x y) x xy 3y e g(x y) x y 1 B {(x y) g(x y) 0} Como g é de classe C 1 e g(x y) (x y) (0 0) em B resulta que os candidatos a extremantes locais são os (x y) que tornam compatível o sistema Ï( x y) g( x y) ( xy 6yx) ( x y) x y Þ Ï 10 xy Ó Ó 10 Ï x y xy x Þ x 3y x 6yxy Þ y xy 10 Ó De e : x y 3y x x y Þ xy y 3xy x Þ x xy y y y 8y 0 Þ x Þ xyou xy Substituindo em : x x 1 Þ 3x 1 1 Þ x Þ y 3 y y 1 Þ 6y 1 1 Þ y Þ x 6 Como é contínua e B compacto basta comparar os valores de nos pontos encontrados: Á ; Á ;
13 Á e Á Portanto Á 6 Á e Á são pontos de máximo e 1 são pontos de mínimo 6 Sejam (x y) x 16y e g(x y) xy 1 x 0 e y 0 Á 6 1 e 6 Resolvendo o sistema: ( x y) g( x y) { xy x ou seja 1 0 0e y 0 ( x 3y) ( y x) Þ xy e 3yx { xy10 Logo x 3 y x 3 y e Daí Þ y x y x Þ x 3y Þ x 16y 0 Þ x y Substituindo em : 1 y 1 Þ y ( y0) Þ x( x0) Ponto de tangência 1 e Curva de nível: x 16y 8 Vamos minimizar a unção dxy ( ) ( x1) ( y1) que nos dá a distância de um ponto P(x y) até (1 1) sujeita à restrição g(x y) y x 0 Para simpliicar cálculos podemos minimizar o quadrado da distância Seja (x y) (x 1) (y 1) (x y) ((x 1) (y 1)) e g(x y) (x 1) Resolvendo o sistema Ï( x y) g( x y) Þ Ï( x1) x yx Ó 0 Ó( y 1) y x 0 Logo 1 x 1 x ( y 1) Þ y x x 151
14 Substituindo em : 1 x x 0 Þ x3 x 1 0 Þ x (as outras raízes são complexas) x e y Portanto ( ) é o ponto procurado 6 Sejam (x y z) x y z e g(x y z) x y 3z Resolvendo o sistema: Ïxyz ( ) gxyz ( ) Þ Ï( x y z) ( 1 3) Óxy3z0 Óxy3z0 Então x ; y ; z 3 Substituindo os valores de x y z em unção de em Þ 1916 Þ Portanto x ; y e z ( x y z)xy z Superície de nível: x y z 3 19 Ponto de tangência Sejam P(x y z) e O(0 0 0) Consideremos a distância entre P e O: dpo ( ) xyz Vamos minimizar a unção (x y) x y z com a restrição g(x y z) x y 3z 0 Ïxyz ( ) gxyz ( ) Þ Ï( x y z) ( 1 3) Óxy3z0 Óxy3z0 3 Temos x ; y e z Substituindo em : 9 0 Þ 7 15
15 6 Então x y e z ) Sejam (x y z) x y 3z g(x y z) x y z e h(x y z) x y z 1 Temos: r i r j r k gxyz ( ) hxyz ( ) x y z gxyz ( ) r r r r hxyz ( ) ( yzi ) ( zx) j( xyk ) 0 em B {(x y z) 3 x y z e x y z 1} (B compacto) Portanto os candidatos a extremantes locais são os (x y z) que tornam compatível o sistema: Ï ( x y z) l g( x y z) m h( x y z) gx ( y z) 0 Ó hx ( y z) 0 Ï( 1 3) l( x y z) m( 111 ) x y z Ó xyz1 Ï1lx m ly m 3lz m x y z Óx y z 1 De segue: ( 0) 1 x Þ x 1 m l y Þ y m l 3 z Þ z 3 m l Substituindo em segue: 1 m m 3 m 1 l l l l l Então m 6 3 l l 1 3 ; x ; y e z l Substituindo em segue: 3 l 1 3 l Á Á 6 l 9 6 l 153
16 Daí Þ Þ 3 Para l 3 temos x ; z Para l 3 temos x 66 1 y z 66 e Logo Á maximiza 13 Seja (x y) x y e g(x y) x 6xy 7y 80 Vamos minimizar (x y) sujeito a restrição g(x y) 0 Ï ( x y) l g( x y) Óx 6xy7y 800 Ou seja Ï( x y) l( x 6y 6x 1y) x 6xy 7y Ó 80 0 x x De : x (x 6y) Þ Þ l x 6y x 3y ( x π 3y) y y (6x 1y) Þ 3x 7y (3x 7y) Logo x y x 3y 3x 7y Þ 3x 8xy 3y 0 8y ± 6y 36y Ï y x x Þ 3 6 Ó x 3 y Substituindo x y 3 em : y 9 y 7y 80 0 Þ 80y 70 Þ y 9 Þ y 3 Þ x 1 15
17 Se x 3y então y Logo os pontos da curva mais próximos da origem são (1 3) e (1 3) Agora os vetores (1 3) e (3 1) são ortogonais [(1 3) (3 1) 0] e r 1 3 u v r 3 1 Á e Á são os versores de (1 3) e (3 1) Fazendo uma mudança de coordenadas: (x y) u Á v Á Æ u (o vetor (x y) escrito em outra base) Logo x u v e y u v Substituindo em x 6xy 7y 80 0 resulta u v Logo a mudança de coordenadas proposta transorma a equação dada na equação u v 1 que é uma 10 0 hipérbole Æ v 3 Sejam T(x y z) 100 x yz e g(x y z) x y z Os únicos pontos críticos no interior da esera x y z que é um conjunto compacto são os pontos (0 y z) (x 0 z) e (x y 0) e nestes pontos a temperatura é zero Para determinar os candidatos que estão na ronteira da esera vamos utilizar os multiplicadores de Lagrange Vamos portanto procurar (x y z) que torne compatível o sistema: Ï T( x y z) l g( x y z) Óg( x y z) 0 Ï( 00xyz 100x z 100x y) l( x y z) x y z Ó 155
18 De segue: 00xyz x Þ yz l x z y Þ x z ly 50 Þ y z e x y 100x y z Þ x lz y 50 Substituindo em y y y Þ y Þ y 1 Þ x Þ z 1 e 100 Logo: ( 1 1) é ponto de máximo e T (x y z) é a temperatura máxima ( 1 1) é ponto de mínimo e T(x y z) 00 é a temperatura mínima 5 Sejam h(x y) x y 6 e g(x y) x y Os vetores h(x y) e g(x y) devem ser paralelos Vamos calcular (x y) que torne compatível o sistema: Ï hx ( y) l gx ( y) Óhx ( y) 0 Þ Ï ( x y) l ( 1 1) Ó x y 60 Ïx l Þ x y Þ x y y l Daí x y 6 0 y y 6y Ó Þ y 1 x Logo P( 1) pertence à elipse (P( 1) não vai atender a condição do problema de minimização da distância) Seja Q(x y) pertencente à reta d(p Q) ( x) ( y1) Vamos minimizar (x y) (x ) (y 1) Procurando (x y) que torne compatível o sistema: Ï ( x y) l g( x y) Ógx ( y) 0 Þ Ï ( ( x ) ( y 1)) l( 1 1) Ó x y 0 Ï x l Þ x y Þ y x 1 y l Daí 5 3 x y x 1 Þ x y Ó e Logo P( 1) e Q 5 3 satisazem a condição do problema 156
MAT-2454 Cálculo Diferencial e Integral II EP-USP
 MAT-454 Cálculo Diferencial e Integral II EP-USP Solução da Questão da Terceira Prova 8//06 Questão (Tipo A Valor: 3, 0 pontos). a. Determine todos os pontos da superfície de nível da função g(x, y, z)
MAT-454 Cálculo Diferencial e Integral II EP-USP Solução da Questão da Terceira Prova 8//06 Questão (Tipo A Valor: 3, 0 pontos). a. Determine todos os pontos da superfície de nível da função g(x, y, z)
CÁLCULO II - MAT 2127 Bacharelado em Química - 2 o Semestre de 2009 Professor Oswaldo Rio Branco
 CÁLCULO II - MAT 7 Bacharelado em Química - o Semestre de 009 Professor Oswaldo Rio Branco MÁXIMOS E MÍNIMOS CONDICIONADOS E MULTIPLICADORES DE LAGRANGE Definições: Seja f : Dom(f) R, Dom(f) R n, n =,
CÁLCULO II - MAT 7 Bacharelado em Química - o Semestre de 009 Professor Oswaldo Rio Branco MÁXIMOS E MÍNIMOS CONDICIONADOS E MULTIPLICADORES DE LAGRANGE Definições: Seja f : Dom(f) R, Dom(f) R n, n =,
15 AULA. Máximos e Mínimos LIVRO. META Encontrar os pontos de máximo e mínimo de uma função de duas variáveis a valores reais.
 1 LIVRO Máximos e Mínimos 1 AULA META Encontrar os pontos de máximo e mínimo de uma função de duas variáveis a valores reais. OBJETIVOS Maximizar e/ou minimizar função de duas variáveis a valores reais.
1 LIVRO Máximos e Mínimos 1 AULA META Encontrar os pontos de máximo e mínimo de uma função de duas variáveis a valores reais. OBJETIVOS Maximizar e/ou minimizar função de duas variáveis a valores reais.
Máximos e mínimos (continuação)
 UNIVERSIDADE FEDERAL DO PARÁ CÁLCULO II - PROJETO NEWTON AULA 3 Assunto: Máximos e mínimos Palavras-chaves: máximos e mínimos, valores máximos e valores mínimos Máximos e mínimos (continuação) Sejam f
UNIVERSIDADE FEDERAL DO PARÁ CÁLCULO II - PROJETO NEWTON AULA 3 Assunto: Máximos e mínimos Palavras-chaves: máximos e mínimos, valores máximos e valores mínimos Máximos e mínimos (continuação) Sejam f
Total Escolha 5 (cinco) questões. Justifique todas as passagens. Não é permitido o uso de calculadoras. Boa Sorte!
 ā Prova de MAT 147 - Cálculo II - FEA-USP 8/11/01 Nome : GABARITO N ō USP : Professor : Oswaldo Rio Branco de Oliveira Q 1 4 5 6 7 Total N Escolha 5 (cinco) questões. Justifique todas as passagens. Não
ā Prova de MAT 147 - Cálculo II - FEA-USP 8/11/01 Nome : GABARITO N ō USP : Professor : Oswaldo Rio Branco de Oliveira Q 1 4 5 6 7 Total N Escolha 5 (cinco) questões. Justifique todas as passagens. Não
Justifique todas as passagens. Boa Sorte! e L 2 : = z 1 3
 3 ā Prova de Cálculo II para Oceanográfico - MAT145 01/12/2010 Nome : GABARITO N ō USP : Professor : Oswaldo Rio Branco de Oliveira Justifique todas as passagens Boa Sorte! Q 1 2 3 4 5 Extra 6 Extra 7
3 ā Prova de Cálculo II para Oceanográfico - MAT145 01/12/2010 Nome : GABARITO N ō USP : Professor : Oswaldo Rio Branco de Oliveira Justifique todas as passagens Boa Sorte! Q 1 2 3 4 5 Extra 6 Extra 7
Derivadas Parciais Capítulo 14
 Derivadas Parciais Capítulo 14 DERIVADAS PARCIAIS No Exemplo 6 da Seção 14.7 maximizamos a função volume V = xyz sujeita à restrição 2xz + 2yz + xy = que expressa a condição de a área da superfície ser
Derivadas Parciais Capítulo 14 DERIVADAS PARCIAIS No Exemplo 6 da Seção 14.7 maximizamos a função volume V = xyz sujeita à restrição 2xz + 2yz + xy = que expressa a condição de a área da superfície ser
Cálculo II. Resumo Teórico Completo
 Cálculo II Resumo Teórico Completo Cálculo 2 A disciplina visa estudar funções e gráficos, de forma semelhante a Cálculo 1, mas expande o estudo para funções de mais de uma variável, bem como gráficos
Cálculo II Resumo Teórico Completo Cálculo 2 A disciplina visa estudar funções e gráficos, de forma semelhante a Cálculo 1, mas expande o estudo para funções de mais de uma variável, bem como gráficos
Cálculo II Lista 5. com respostas
 Cálculo II Lista 5. com respostas Exercício 1. Determine os pontos críticos das funções dadas e classifique-os, decidindo se são pontos de máximo local, de mínimo local ou de sela: (a) f(x, y) = x 2 +
Cálculo II Lista 5. com respostas Exercício 1. Determine os pontos críticos das funções dadas e classifique-os, decidindo se são pontos de máximo local, de mínimo local ou de sela: (a) f(x, y) = x 2 +
1o sem profa. daniela m. vieira. (a) f(x, y) = 3x y no conjunto A de todos (x, y) tais que x 0, y 0, y x 3, x + y 4 e
 mat51 - cálculo várias variáveis i - licenciatura 1o sem 011 - profa daniela m vieira SÉTIMA LISTA DE EXERCÍCIOS (1) Estude a função dada com relação a máximo e mínimo no conjunto dado (a) f(x, y) = x
mat51 - cálculo várias variáveis i - licenciatura 1o sem 011 - profa daniela m vieira SÉTIMA LISTA DE EXERCÍCIOS (1) Estude a função dada com relação a máximo e mínimo no conjunto dado (a) f(x, y) = x
Nos pontos (x, y), x 0 ou y 0, f(x, y) não está definida, logo nestes pontos f não é diferenciável. Seja, então, (x, y), com x 0 e y 0.
 CAPÍTULO Eercícios d) (, y) y Nos pontos (, y), ou y, (, y) não está deinida, logo nestes pontos não é dierenciável Seja, então, (, y), com e y Ï Ôa) admite derivadas parciais em (, y) Ô é dierenciável
CAPÍTULO Eercícios d) (, y) y Nos pontos (, y), ou y, (, y) não está deinida, logo nestes pontos não é dierenciável Seja, então, (, y), com e y Ï Ôa) admite derivadas parciais em (, y) Ô é dierenciável
xy 2 (b) A função é contínua na origem? Justique sua resposta! (a) Calculando o limite pela reta y = mx:
 NOME: UNIVERSIDADE FEDERAL DO RIO DE JANEIRO Instituto de Matemática PRIMEIRA PROVA UNIFICADA CÁLCULO II Politécnica, Engenharia Química e Ciência da Computação 21/05/2013. 1 a QUESTÃO : Dada a função
NOME: UNIVERSIDADE FEDERAL DO RIO DE JANEIRO Instituto de Matemática PRIMEIRA PROVA UNIFICADA CÁLCULO II Politécnica, Engenharia Química e Ciência da Computação 21/05/2013. 1 a QUESTÃO : Dada a função
Cálculo II. Resumo e Exercícios P3
 Cálculo II Resumo e Exercícios P3 Resuminho Teórico e Fórmulas Parte 1 Funções de Três Variáveis w = f(x, y, z) Definida em R +, apenas um valor de w para cada (x, y, z). Domínio de Função de Três Variáveis:
Cálculo II Resumo e Exercícios P3 Resuminho Teórico e Fórmulas Parte 1 Funções de Três Variáveis w = f(x, y, z) Definida em R +, apenas um valor de w para cada (x, y, z). Domínio de Função de Três Variáveis:
MAT 2454 Cálculo II Resolução da Lista 3
 MAT 2454 Cálculo II Resolução da Lista 3 por César Morad I. Superfícies de Nível, Planos Tangentes e Derivadas Direcionais 1.1. Em cada caso, esboce a superfície de nível c da função F: R 2 R: a. F(x,
MAT 2454 Cálculo II Resolução da Lista 3 por César Morad I. Superfícies de Nível, Planos Tangentes e Derivadas Direcionais 1.1. Em cada caso, esboce a superfície de nível c da função F: R 2 R: a. F(x,
Multiplicadores de Lagrange
 Multiplicadores de Lagrange Para motivar o método, suponha que queremos maximizar uma função f (x, y) sujeito a uma restrição g(x, y) = 0. Geometricamente: queremos um ponto sobre o gráfico da curva de
Multiplicadores de Lagrange Para motivar o método, suponha que queremos maximizar uma função f (x, y) sujeito a uma restrição g(x, y) = 0. Geometricamente: queremos um ponto sobre o gráfico da curva de
CAPÍTULO 8. Exercícios 8.1. Seja f(x, y) 3x 2y. a) f(1, 1) ( 1) Seja f ( x y. , ou seja, d) f( x, y) x2 y2. Temos
 CAPÍTULO 8 Eerccios 8 Seja f(, ) 3 a) f(, ) 3 () d) f(, k) f(, ) 3 k 3 k k Seja f (, ) a) D( f) {(, ) π 0}, ou seja, D( f) {(, ) π } 4 f(, ) a b Temos f(, 0) a Þ a e f(0, ) b Þ b 3 Logo, f(, ) a 3b 5 a)
CAPÍTULO 8 Eerccios 8 Seja f(, ) 3 a) f(, ) 3 () d) f(, k) f(, ) 3 k 3 k k Seja f (, ) a) D( f) {(, ) π 0}, ou seja, D( f) {(, ) π } 4 f(, ) a b Temos f(, 0) a Þ a e f(0, ) b Þ b 3 Logo, f(, ) a 3b 5 a)
Aula Distância entre duas retas paralelas no espaço. Definição 1. Exemplo 1
 Aula 1 Sejam r 1 = P 1 + t v 1 t R} e r 2 = P 2 + t v 2 t R} duas retas no espaço. Se r 1 r 2, sabemos que r 1 e r 2 são concorrentes (isto é r 1 r 2 ) ou não se intersectam. Quando a segunda possibilidade
Aula 1 Sejam r 1 = P 1 + t v 1 t R} e r 2 = P 2 + t v 2 t R} duas retas no espaço. Se r 1 r 2, sabemos que r 1 e r 2 são concorrentes (isto é r 1 r 2 ) ou não se intersectam. Quando a segunda possibilidade
CÁLCULO II - MAT 145 Bacharelado Oceanografia - 2 semestre de 2010 Professor Oswaldo Rio Branco
 CÁLCULO II - MAT 145 Bacharelado Oceanografia - 2 semestre de 2010 Professor Oswaldo Rio Branco DÚVIDAS (7) (L1) Se r= x,y,r 1 = x 1,y 1,r 2 = x 2,y 2, descreva o cjto. dos pontos(x,y) tais que r r 1 +
CÁLCULO II - MAT 145 Bacharelado Oceanografia - 2 semestre de 2010 Professor Oswaldo Rio Branco DÚVIDAS (7) (L1) Se r= x,y,r 1 = x 1,y 1,r 2 = x 2,y 2, descreva o cjto. dos pontos(x,y) tais que r r 1 +
MAT Cálculo Diferencial e Integral para Engenharia II 3 a lista de exercícios
 MAT44 - Cálculo Diferencial e Integral para Engenharia II a lista de exercícios - 01 1. Esboce a superfície de nível da função F : A R R para o nível c: a) F(x, y, z) = x+y+z e c = 1 b) F(x, y, z) = x
MAT44 - Cálculo Diferencial e Integral para Engenharia II a lista de exercícios - 01 1. Esboce a superfície de nível da função F : A R R para o nível c: a) F(x, y, z) = x+y+z e c = 1 b) F(x, y, z) = x
Derivadas Parciais Capítulo 14
 Derivadas Parciais Capítulo 14 DERIVADAS PARCIAIS Como vimos no Capítulo 4, no Volume I, um dos principais usos da derivada ordinária é na determinação dos valores máximo e mínimo. DERIVADAS PARCIAIS 14.7
Derivadas Parciais Capítulo 14 DERIVADAS PARCIAIS Como vimos no Capítulo 4, no Volume I, um dos principais usos da derivada ordinária é na determinação dos valores máximo e mínimo. DERIVADAS PARCIAIS 14.7
J. Delgado - K. Frensel - L. Crissaff Geometria Analítica e Cálculo Vetorial
 178 Capítulo 10 Equação da reta e do plano no espaço 1. Equações paramétricas da reta no espaço Sejam A e B dois pontos distintos no espaço e seja r a reta que os contém. Então, P r existe t R tal que
178 Capítulo 10 Equação da reta e do plano no espaço 1. Equações paramétricas da reta no espaço Sejam A e B dois pontos distintos no espaço e seja r a reta que os contém. Então, P r existe t R tal que
Aula 18. Método Multiplicadores Lagrange (continuação)
 Aula 18 Método Multiplicadores Lagrange (continuação) Na aula anterior introduzimos o Método dos Multiplicadores de Lagrange, que serve para maximizar/minimizar uma função restrita a um domínio do tipo
Aula 18 Método Multiplicadores Lagrange (continuação) Na aula anterior introduzimos o Método dos Multiplicadores de Lagrange, que serve para maximizar/minimizar uma função restrita a um domínio do tipo
MAT Cálculo 2 para Economia 3 a Prova - 28 de novembro de 2016
 MAT 0147 - Cálculo para Economia 3 a Prova - 8 de novembro de 016 Questão 1) Determine o máximo e o mínimo de f(x, y) = x 4 + y em D = {(x, y); x + y 1}. Soluç~ao: As derivadas parciais f x (x, y) = 4x
MAT 0147 - Cálculo para Economia 3 a Prova - 8 de novembro de 016 Questão 1) Determine o máximo e o mínimo de f(x, y) = x 4 + y em D = {(x, y); x + y 1}. Soluç~ao: As derivadas parciais f x (x, y) = 4x
DERIVADAS PARCIAIS. y = lim
 DERIVADAS PARCIAIS Definição: Seja f uma função de duas variáveis, x e y (f: D R onde D R 2 ) e (x 0, y 0 ) é um ponto no domínio de f ((x 0, y 0 ) D). A derivada parcial de f em relação a x no ponto (x
DERIVADAS PARCIAIS Definição: Seja f uma função de duas variáveis, x e y (f: D R onde D R 2 ) e (x 0, y 0 ) é um ponto no domínio de f ((x 0, y 0 ) D). A derivada parcial de f em relação a x no ponto (x
Geometria Analítica - Aula
 Geometria Analítica - Aula 19 246 IM-UFF K. Frensel - J. Delgado Aula 20 Vamos analisar a equação Ax 2 + Cy 2 + Dx + Ey + F = 0 nos casos em que exatamente um dos coeficientes A ou C é nulo. 1. Parábola
Geometria Analítica - Aula 19 246 IM-UFF K. Frensel - J. Delgado Aula 20 Vamos analisar a equação Ax 2 + Cy 2 + Dx + Ey + F = 0 nos casos em que exatamente um dos coeficientes A ou C é nulo. 1. Parábola
MAT Cálculo Diferencial e Integral para Engenharia II 2 o semestre de Prova Substitutiva - 03/12/2012. Gabarito - TURMA A
 MAT 25 - Cálculo Diferencial e Integral para Engenharia II 2 o semestre de 2012 - Prova Substitutiva - 0/12/2012 Gabarito - TURMA A Questão 1.( pontos) Seja a função f(x,y) = ( ) x5 sen x +y x 2 +y 2,
MAT 25 - Cálculo Diferencial e Integral para Engenharia II 2 o semestre de 2012 - Prova Substitutiva - 0/12/2012 Gabarito - TURMA A Questão 1.( pontos) Seja a função f(x,y) = ( ) x5 sen x +y x 2 +y 2,
Máximos e mínimos UNIVERSIDADE FEDERAL DO PARÁ CÁLCULO II - PROJETO NEWTON AULA 22. Assunto: Máximos e mínimos
 Assunto: Máximos e mínimos UNIVERSIDADE FEDERAL DO PARÁ CÁLCULO II - PROJETO NEWTON AULA Palavras-chaves: máximos e mínimos, valores máximos e valores mínimos Máximos e mínimos Sejam f uma função a valores
Assunto: Máximos e mínimos UNIVERSIDADE FEDERAL DO PARÁ CÁLCULO II - PROJETO NEWTON AULA Palavras-chaves: máximos e mínimos, valores máximos e valores mínimos Máximos e mínimos Sejam f uma função a valores
CÁLCULO II Prof. Jerônimo Monteiro
 CÁLCULO II Pro. Jerônimo Monteiro Gabarito - Lista Semanal 08 Questão 1. Calcule 2 para (x, y, onde x = r cos θ e y = r sen θ. 2 Solução: Primeiro, calculamos pela regra da cadeia, como segue: = + = (
CÁLCULO II Pro. Jerônimo Monteiro Gabarito - Lista Semanal 08 Questão 1. Calcule 2 para (x, y, onde x = r cos θ e y = r sen θ. 2 Solução: Primeiro, calculamos pela regra da cadeia, como segue: = + = (
Geometria Analítica II - Aula 5 108
 Geometria Analítica II - Aula 5 108 IM-UFF Aula 6 Superfícies Cilíndricas Sejam γ uma curva contida num plano π do espaço e v 0 um vetor não-paralelo ao plano π. A superfície cilíndrica S de diretriz γ
Geometria Analítica II - Aula 5 108 IM-UFF Aula 6 Superfícies Cilíndricas Sejam γ uma curva contida num plano π do espaço e v 0 um vetor não-paralelo ao plano π. A superfície cilíndrica S de diretriz γ
Aula 15. Derivadas Direcionais e Vetor Gradiente. Quando u = (1, 0) ou u = (0, 1), obtemos as derivadas parciais em relação a x ou y, respectivamente.
 Aula 15 Derivadas Direcionais e Vetor Gradiente Seja f(x, y) uma função de variáveis. Iremos usar a notação D u f(x 0, y 0 ) para: Derivada direcional de f no ponto (x 0, y 0 ), na direção do vetor unitário
Aula 15 Derivadas Direcionais e Vetor Gradiente Seja f(x, y) uma função de variáveis. Iremos usar a notação D u f(x 0, y 0 ) para: Derivada direcional de f no ponto (x 0, y 0 ), na direção do vetor unitário
Aula Exemplos diversos. Exemplo 1
 Aula 3 1. Exemplos diversos Exemplo 1 Determine a equação da hipérbole equilátera, H, que passa pelo ponto Q = ( 1, ) e tem os eixos coordenados como assíntotas. Como as assíntotas da hipérbole são os
Aula 3 1. Exemplos diversos Exemplo 1 Determine a equação da hipérbole equilátera, H, que passa pelo ponto Q = ( 1, ) e tem os eixos coordenados como assíntotas. Como as assíntotas da hipérbole são os
Total Escolha 5 (cinco) questões. Justifique todas as passagens. Boa Sorte!
 ā Prova de MAT 147 - Cálculo II - FEA-USP 15/10/01 Nome : GABARITO N ō USP : Professor : Oswaldo Rio Branco de Oliveira Q 1 3 4 5 6 7 Total N Escolha 5 (cinco) questões. Justifique todas as passagens.
ā Prova de MAT 147 - Cálculo II - FEA-USP 15/10/01 Nome : GABARITO N ō USP : Professor : Oswaldo Rio Branco de Oliveira Q 1 3 4 5 6 7 Total N Escolha 5 (cinco) questões. Justifique todas as passagens.
MAT Cálculo Diferencial e Integral para Engenharia II 2 o semestre de Prova Substitutiva - 03/12/2012. Gabarito - TURMA A
 MAT 25 - Cálculo Diferencial e Integral para Engenaria II 2 o semestre de 2012 - Prova Substitutiva - 0/12/2012 Gabarito - TURMA A Questão 1. pontos) Seja a função fx,y) = ) x5 sen x +y x 2 +y 2, se x,y)
MAT 25 - Cálculo Diferencial e Integral para Engenaria II 2 o semestre de 2012 - Prova Substitutiva - 0/12/2012 Gabarito - TURMA A Questão 1. pontos) Seja a função fx,y) = ) x5 sen x +y x 2 +y 2, se x,y)
MATEMÁTICA A - 11o Ano Funções - Derivada (extremos, monotonia e retas tangentes) Propostas de resolução
 MATEMÁTICA A - o Ano Funções - Derivada extremos, monotonia e retas tangentes) Propostas de resolução Exercícios de exames e testes intermédios. Temos que, pela definição de derivada num ponto, f ) fx)
MATEMÁTICA A - o Ano Funções - Derivada extremos, monotonia e retas tangentes) Propostas de resolução Exercícios de exames e testes intermédios. Temos que, pela definição de derivada num ponto, f ) fx)
Respostas sem justificativas não serão aceitas Não é permitido o uso de aparelhos eletrônicos
 UNIVERSIDADE FEDERAL RURAL DE PERNAMBUCO UNIDADE ACADÊMICA DO CABO DE SANTO AGOSTINHO CÁLCULO DIFERENCIAL E INTEGRAL - 018. - TURMA MA 1A VERIFICAÇÃO DE APRENDIZAGEM - PARTE Nome Legível RG CPF Respostas
UNIVERSIDADE FEDERAL RURAL DE PERNAMBUCO UNIDADE ACADÊMICA DO CABO DE SANTO AGOSTINHO CÁLCULO DIFERENCIAL E INTEGRAL - 018. - TURMA MA 1A VERIFICAÇÃO DE APRENDIZAGEM - PARTE Nome Legível RG CPF Respostas
Lista Determine o valor máximo e o valor mínimo da função f sujeita às restrições explicitadas:
 UFPR - Universidade Federal do Paraná Setor de Ciências Exatas Departamento de Matemática CM048 - Cálculo II - Matemática Diurno Prof. Zeca Eidam Lista 3 Máximos e mínimos de funções de duas variáveis
UFPR - Universidade Federal do Paraná Setor de Ciências Exatas Departamento de Matemática CM048 - Cálculo II - Matemática Diurno Prof. Zeca Eidam Lista 3 Máximos e mínimos de funções de duas variáveis
Aula Exemplos e aplicações. Exemplo 1. Nesta aula apresentamos uma série de exemplos e aplicações dos conceitos vistos.
 Aula 16 Nesta aula apresentamos uma série de exemplos e aplicações dos conceitos vistos. 1. Exemplos e aplicações Exemplo 1 Considere os pontos A = (1, 2, 2), B = (2, 4, 3), C = ( 1, 4, 2), D = (7, 1,
Aula 16 Nesta aula apresentamos uma série de exemplos e aplicações dos conceitos vistos. 1. Exemplos e aplicações Exemplo 1 Considere os pontos A = (1, 2, 2), B = (2, 4, 3), C = ( 1, 4, 2), D = (7, 1,
MAT Cálculo Diferencial e Integral para Engenharia II 3 a lista de exercícios
 MAT454 - Cálculo Diferencial e Integral para Engenharia II a lista de exercícios - 014 1. Em cada caso, esboce a superfície de nível c da função F : R R: a) Fx, y, z) = x + y + z e c = 1 b) Fx, y, z) =
MAT454 - Cálculo Diferencial e Integral para Engenharia II a lista de exercícios - 014 1. Em cada caso, esboce a superfície de nível c da função F : R R: a) Fx, y, z) = x + y + z e c = 1 b) Fx, y, z) =
Funções de Uma Variável - 1 a Avaliação - Turma B3 31 de outubro de Prof. Armando Caputi
 Funções de Uma Variável - 1 a Avaliação - Turma B 1 de outubro de 017 - Prof. Armando Caputi 1 Determine o domínio da função f(x) = arctan x x + 1 (justifique) e a equação da reta tangente ao seu gráfico
Funções de Uma Variável - 1 a Avaliação - Turma B 1 de outubro de 017 - Prof. Armando Caputi 1 Determine o domínio da função f(x) = arctan x x + 1 (justifique) e a equação da reta tangente ao seu gráfico
CÁLCULO III - MAT 216- IFUSP- Semestre 1 de 2014 Professor Oswaldo Rio Branco de Oliveira
 CÁLCULO III - MAT 16- IFUSP- Semestre 1 de 014 Professor Oswaldo Rio Branco de Oliveira http://www.ime.usp.br/~oliveira MULTIPLICADORES DE LAGRANGE: INTERPRETAÇÕES E EXEMPLOS Definições: Seja f Ω R, com
CÁLCULO III - MAT 16- IFUSP- Semestre 1 de 014 Professor Oswaldo Rio Branco de Oliveira http://www.ime.usp.br/~oliveira MULTIPLICADORES DE LAGRANGE: INTERPRETAÇÕES E EXEMPLOS Definições: Seja f Ω R, com
MAT Lista de exercícios
 1 Curvas no R n 1. Esboce a imagem das seguintes curvas para t R a) γ(t) = (1, t) b) γ(t) = (t, cos(t)) c) γ(t) = (t, t ) d) γ(t) = (cos(t), sen(t), 2t) e) γ(t) = (t, 2t, 3t) f) γ(t) = ( 2 cos(t), 2sen(t))
1 Curvas no R n 1. Esboce a imagem das seguintes curvas para t R a) γ(t) = (1, t) b) γ(t) = (t, cos(t)) c) γ(t) = (t, t ) d) γ(t) = (cos(t), sen(t), 2t) e) γ(t) = (t, 2t, 3t) f) γ(t) = ( 2 cos(t), 2sen(t))
MAT Cálculo II - IQ Prof. Oswaldo Rio Branco de Oliveira 2 ō semestre de 2008 Prova Substitutiva
 MAT212 - Cálculo II - IQ Prof. Oswaldo Rio Branco de Oliveira 2 ō semestre de 2008 Prova Substitutiva Nome : N ō USP : GABARITO Q 1 2 3 4 5 6 Total N 1. Seja f(x, y) = 2xy2, se (x, y) (0, 0), f(0, 0) =
MAT212 - Cálculo II - IQ Prof. Oswaldo Rio Branco de Oliveira 2 ō semestre de 2008 Prova Substitutiva Nome : N ō USP : GABARITO Q 1 2 3 4 5 6 Total N 1. Seja f(x, y) = 2xy2, se (x, y) (0, 0), f(0, 0) =
Cálculo 2. Guia de Estudos P1
 Cálculo 2 Guia de Estudos P1 Resuminho Teórico e Fórmulas Parte 1 Cônicas Conceito: Cônicas são formas desenhadas em duas dimensões, considerando apenas os eixos x (horizontal) e y (vertical). Tipos de
Cálculo 2 Guia de Estudos P1 Resuminho Teórico e Fórmulas Parte 1 Cônicas Conceito: Cônicas são formas desenhadas em duas dimensões, considerando apenas os eixos x (horizontal) e y (vertical). Tipos de
21 e 22. Superfícies Quádricas. Sumário
 21 e 22 Superfícies uádricas Sumário 21.1 Introdução....................... 2 21.2 Elipsoide........................ 3 21.3 Hiperboloide de uma Folha.............. 4 21.4 Hiperboloide de duas folhas..............
21 e 22 Superfícies uádricas Sumário 21.1 Introdução....................... 2 21.2 Elipsoide........................ 3 21.3 Hiperboloide de uma Folha.............. 4 21.4 Hiperboloide de duas folhas..............
CÁLCULO III - MAT Encontre todos os máximos locais, mínimos locais e pontos de sela nas seguintes funções:
 UNIVERSIDADE FEDERAL DA INTEGRAÇÃO LATINO-AMERICANA Instituto Latino-Americano de Ciências da Vida e da Natureza Centro Interdisciplinar de Ciências da Natureza CÁLCULO III - MAT0036 9 a Lista de exercícios
UNIVERSIDADE FEDERAL DA INTEGRAÇÃO LATINO-AMERICANA Instituto Latino-Americano de Ciências da Vida e da Natureza Centro Interdisciplinar de Ciências da Natureza CÁLCULO III - MAT0036 9 a Lista de exercícios
Geometria Analítica II - Aula 4 82
 Geometria Analítica II - Aula 4 8 IM-UFF K. Frensel - J. Delgado Aula 5 Esferas Iniciaremos o nosso estudo sobre superfícies com a esfera, que já nos é familiar. A esfera S de centro no ponto A e raio
Geometria Analítica II - Aula 4 8 IM-UFF K. Frensel - J. Delgado Aula 5 Esferas Iniciaremos o nosso estudo sobre superfícies com a esfera, que já nos é familiar. A esfera S de centro no ponto A e raio
MAT Cálculo Diferencial e Integral para Engenharia II 3 a lista de exercícios
 MAT 454 - Cálculo Diferencial e Integral para Engenharia II a lista de exercícios - 7. Ache os pontos do hiperbolóide x y + z = onde a reta normal é paralela à reta que une os pontos (,, ) e (5,, 6)..
MAT 454 - Cálculo Diferencial e Integral para Engenharia II a lista de exercícios - 7. Ache os pontos do hiperbolóide x y + z = onde a reta normal é paralela à reta que une os pontos (,, ) e (5,, 6)..
Geometria Analítica I
 Geom. Analítica I Respostas do Módulo I - Aula 15 1 Geometria Analítica I 17/03/2011 Respostas dos Exercícios do Módulo I - Aula 15 Aula 15 1. Este exercício se resume a escrever a equação em uma das formas
Geom. Analítica I Respostas do Módulo I - Aula 15 1 Geometria Analítica I 17/03/2011 Respostas dos Exercícios do Módulo I - Aula 15 Aula 15 1. Este exercício se resume a escrever a equação em uma das formas
O problema proposto possui alguma solução? Se sim, quantas e quais são elas?
 PROVA PARA OS ALUNOS DE 3º ANO DO ENSINO MÉDIO 1) Considere o seguinte problema: Vitor ganhou R$ 3,20 de seu pai em moedas de 5 centavos, 10 centavos e 25 centavos. Se recebeu um total de 50 moedas, quantas
PROVA PARA OS ALUNOS DE 3º ANO DO ENSINO MÉDIO 1) Considere o seguinte problema: Vitor ganhou R$ 3,20 de seu pai em moedas de 5 centavos, 10 centavos e 25 centavos. Se recebeu um total de 50 moedas, quantas
1 Derivadas Parciais de Ordem Superior Em duas variáveis Em três variáveis. 1.3 Derivadas de Ordem
 Contents 1 Derivadas Parciais de Ordem Superior 1 1.1 Em duas variáveis..................................... 1 1. Em três variáveis...................................... 1 1.3 Derivadas de Ordem...................................
Contents 1 Derivadas Parciais de Ordem Superior 1 1.1 Em duas variáveis..................................... 1 1. Em três variáveis...................................... 1 1.3 Derivadas de Ordem...................................
Instituto de Matemática - IM/UFRJ Cálculo I - MAC118 1 a Prova - Gabarito - 13/10/2016
 Instituto de Matemática - IM/UFRJ Cálculo I - MAC118 1 a Prova - Gabarito - 13/10/2016 Questão 1: (2 pontos) x (a) (0.4 ponto) Calcule o ite: 2 + 3 2. x 1 x 1 ( πx + 5 ) (b) (0.4 ponto) Calcule o ite:
Instituto de Matemática - IM/UFRJ Cálculo I - MAC118 1 a Prova - Gabarito - 13/10/2016 Questão 1: (2 pontos) x (a) (0.4 ponto) Calcule o ite: 2 + 3 2. x 1 x 1 ( πx + 5 ) (b) (0.4 ponto) Calcule o ite:
1. A partir da definição, determinar a equação da parábola P, cujo foco é F = (3, 4) e cuja diretriz é L : x + y 2 = 0. (x 3) 2 + (y + 4) 2 =
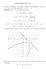 QUESTÕES-AULA 18 1. A partir da definição, determinar a equação da parábola P, cujo foco é F = (3, 4) e cuja diretriz é L : x + y = 0. Solução Seja P = (x, y) R. Temos que P P d(p, F ) = d(p, L) (x 3)
QUESTÕES-AULA 18 1. A partir da definição, determinar a equação da parábola P, cujo foco é F = (3, 4) e cuja diretriz é L : x + y = 0. Solução Seja P = (x, y) R. Temos que P P d(p, F ) = d(p, L) (x 3)
Matemática 2. Teste Final. Atenção: Esta prova deve ser entregue ao fim de 1 Hora. Deve justificar detalhadamente todas as suas respostas.
 Matemática 2 Lic. em Economia, Gestão e Finanças Data: 4 de Julho de 2017 Duração: 1H Teste Final Atenção: Esta prova deve ser entregue ao fim de 1 Hora. Deve justificar detalhadamente todas as suas respostas.
Matemática 2 Lic. em Economia, Gestão e Finanças Data: 4 de Julho de 2017 Duração: 1H Teste Final Atenção: Esta prova deve ser entregue ao fim de 1 Hora. Deve justificar detalhadamente todas as suas respostas.
Funções de Uma Variável - 1 a Avaliação - Turma B3 31 de outubro de Prof. Armando Caputi
 Funções de Uma Variável - 1 a Avaliação - Turma B 1 de outubro de 017 - Prof. Armando Caputi 1 Determine o domínio da função g(x) = arctan ( ln(x x + ) ) (justifique) e a equação da reta tangente ao seu
Funções de Uma Variável - 1 a Avaliação - Turma B 1 de outubro de 017 - Prof. Armando Caputi 1 Determine o domínio da função g(x) = arctan ( ln(x x + ) ) (justifique) e a equação da reta tangente ao seu
*** Escolha e resolva 4 das 6 questões! *** *** Justifique TODAS as suas respostas! *** + µ(x, y)sen(89x + π) 0 φ 6 (x, y) + µ 6 (x, y) 1.
 USP/ICMC/SMA - Gabarito da 1 a Prova de Cálculo II - SMA- 11/10/006 Professora: Márcia Federson *** Escolha e resolva das 6 questões! *** *** Justifique TODAS as suas respostas! *** Questão 1 Sejam φ :
USP/ICMC/SMA - Gabarito da 1 a Prova de Cálculo II - SMA- 11/10/006 Professora: Márcia Federson *** Escolha e resolva das 6 questões! *** *** Justifique TODAS as suas respostas! *** Questão 1 Sejam φ :
P4 de Cálculo a Várias Variáveis I MAT Data: 02 de julho
 P de Cálculo a Várias Variáveis I MAT 6 03. Data: 0 de julho Nome: Assinatura: Matrícula: Turma: Questão Valor Nota Revisão 5.0 5.0 Total 0.0 Instruções Mantenha seu celular desligado durante toda a prova.
P de Cálculo a Várias Variáveis I MAT 6 03. Data: 0 de julho Nome: Assinatura: Matrícula: Turma: Questão Valor Nota Revisão 5.0 5.0 Total 0.0 Instruções Mantenha seu celular desligado durante toda a prova.
FICHA de AVALIAÇÃO de MATEMÁTICA A 11.º Ano Versão 3
 FICHA de AVALIAÇÃO de MATEMÁTICA A.º Ano Versão Nome: N.º Turma: Apresente o seu raciocínio de orma clara, indicando todos os cálculos que tiver de eetuar e todas as justiicações necessárias. Quando, para
FICHA de AVALIAÇÃO de MATEMÁTICA A.º Ano Versão Nome: N.º Turma: Apresente o seu raciocínio de orma clara, indicando todos os cálculos que tiver de eetuar e todas as justiicações necessárias. Quando, para
Concluimos dai que o centro da circunferência é C = (6, 4) e o raio é
 QUESTÕES-AULA 17 1. A equação x 2 + y 2 12x + 8y + 0 = 0 representa uma circunferência de centro C = (a, b) e de raio R. Determinar o valor de a + b + R. Solução Completamos quadrados na expressão dada.
QUESTÕES-AULA 17 1. A equação x 2 + y 2 12x + 8y + 0 = 0 representa uma circunferência de centro C = (a, b) e de raio R. Determinar o valor de a + b + R. Solução Completamos quadrados na expressão dada.
Aula Exemplos e aplicações - continuação. Exemplo 8. Nesta aula continuamos com mais exemplos e aplicações dos conceitos vistos.
 Aula 1 Nesta aula continuamos com mais exemplos e aplicações dos conceitos vistos. 1. Exemplos e aplicações - continuação Exemplo 8 Considere o plano π : x + y + z = 3 e a reta r paralela ao vetor v =
Aula 1 Nesta aula continuamos com mais exemplos e aplicações dos conceitos vistos. 1. Exemplos e aplicações - continuação Exemplo 8 Considere o plano π : x + y + z = 3 e a reta r paralela ao vetor v =
0 < c < a ; d(f 1, F 2 ) = 2c
 Capítulo 14 Elipse Nosso objetivo, neste e nos próximos capítulos, é estudar a equação geral do segundo grau em duas variáveis: Ax + Bxy + Cy + Dx + Ey + F = 0, onde A 0 ou B 0 ou C 0 Para isso, deniremos,
Capítulo 14 Elipse Nosso objetivo, neste e nos próximos capítulos, é estudar a equação geral do segundo grau em duas variáveis: Ax + Bxy + Cy + Dx + Ey + F = 0, onde A 0 ou B 0 ou C 0 Para isso, deniremos,
Aula Elipse. Definição 1. Nosso objetivo agora é estudar a equação geral do segundo grau em duas variáveis:
 Aula 18 Nosso objetivo agora é estudar a equação geral do segundo grau em duas variáveis: Ax + Bxy + Cy + Dx + Ey + F = 0, onde A 0 ou B 0 ou C 0 Vamos considerar primeiro os casos em que B = 0. Isto é,
Aula 18 Nosso objetivo agora é estudar a equação geral do segundo grau em duas variáveis: Ax + Bxy + Cy + Dx + Ey + F = 0, onde A 0 ou B 0 ou C 0 Vamos considerar primeiro os casos em que B = 0. Isto é,
Geometria Analítica. Estudo do Plano. Prof Marcelo Maraschin de Souza
 Geometria Analítica Estudo do Plano Prof Marcelo Maraschin de Souza Plano Equação Geral do Plano Seja A(x 1, y 1, z 1 ) um ponto pertencente a um plano π e n = a, b, c, n 0, um vetor normal (ortogonal)
Geometria Analítica Estudo do Plano Prof Marcelo Maraschin de Souza Plano Equação Geral do Plano Seja A(x 1, y 1, z 1 ) um ponto pertencente a um plano π e n = a, b, c, n 0, um vetor normal (ortogonal)
GGM Geometria Analítica e Cálculo Vetorial Geometria Analítica Básica 20/12/2012- GGM - UFF Dirce Uesu
 GGM0016 Geometria Analítica e Cálculo Vetorial Geometria Analítica Básica 0/1/01- GGM - UFF Dirce Uesu CÔNICAS DEFINIÇÃO GEOMÉTRICA Exercício: Acesse o sitio abaixo e use o programa: http://www.professores.uff.br/hjbortol/disciplinas/005.1/gma04096/applets/conic/co
GGM0016 Geometria Analítica e Cálculo Vetorial Geometria Analítica Básica 0/1/01- GGM - UFF Dirce Uesu CÔNICAS DEFINIÇÃO GEOMÉTRICA Exercício: Acesse o sitio abaixo e use o programa: http://www.professores.uff.br/hjbortol/disciplinas/005.1/gma04096/applets/conic/co
CAPÍTULO 16 REAIS DE VÁRIAS VARIÁVEIS EM COMPACTOS
 CAPÍTULO 16 MÁXIMOS E MÍNIMOS DE FUNÇÕES REAIS DE VÁRIAS VARIÁVEIS EM COMPACTOS 161 Introdução Esta aula está baseada no Capítulo 16 do segundo volume do livro de Cálculo do Guidorii Nesta aula, estamos
CAPÍTULO 16 MÁXIMOS E MÍNIMOS DE FUNÇÕES REAIS DE VÁRIAS VARIÁVEIS EM COMPACTOS 161 Introdução Esta aula está baseada no Capítulo 16 do segundo volume do livro de Cálculo do Guidorii Nesta aula, estamos
Noções de matemática. Maurício Yoshida Izumi
 Noções de matemática Maurício Yosida Izumi 29 de agosto de 2015 Sumário 1 Notação e funções 2 1.1 Números reais........................................ 2 1.2 Intervalos...........................................
Noções de matemática Maurício Yosida Izumi 29 de agosto de 2015 Sumário 1 Notação e funções 2 1.1 Números reais........................................ 2 1.2 Intervalos...........................................
ln(x + y) (x + y 1) < 1 (x + y 1)2 3. Determine o polinômio de Taylor de ordem 2 da função dada, em volta do ponto dado:
 ā Lista de MAT 454 - Cálculo II - a) POLINÔMIOS DE TAYLOR 1. Seja f(x, y) = ln (x + y). a) Determine o polinômio de Taylor de ordem um de f em torno de ( 1, 1 ). b) Mostre que para todo (x, y) IR com x
ā Lista de MAT 454 - Cálculo II - a) POLINÔMIOS DE TAYLOR 1. Seja f(x, y) = ln (x + y). a) Determine o polinômio de Taylor de ordem um de f em torno de ( 1, 1 ). b) Mostre que para todo (x, y) IR com x
BANCO DE EXERCÍCIOS - 24 HORAS
 BANCO DE EXERCÍCIOS - HORAS 9º ANO ESPECIALIZADO/CURSO ESCOLAS TÉCNICAS E MILITARES FOLHA Nº GABARITO COMENTADO ) A função será y,5x +, onde y (preço a ser pago) está em função de x (número de quilômetros
BANCO DE EXERCÍCIOS - HORAS 9º ANO ESPECIALIZADO/CURSO ESCOLAS TÉCNICAS E MILITARES FOLHA Nº GABARITO COMENTADO ) A função será y,5x +, onde y (preço a ser pago) está em função de x (número de quilômetros
Aula 17 Superfícies quádricas - parabolóides
 Objetivos Aula 17 Superfícies quádricas - parabolóides Apresentar os parabolóides elípticos e hiperbólicos identificando suas seções planas. Estudar os parabolóides regrados e de revolução. Nas superfícies
Objetivos Aula 17 Superfícies quádricas - parabolóides Apresentar os parabolóides elípticos e hiperbólicos identificando suas seções planas. Estudar os parabolóides regrados e de revolução. Nas superfícies
Nome do aluno: N.º: Para responder aos itens de escolha múltipla, não apresente cálculos nem justificações e escreva, na folha de respostas:
 Teste de Matemática A 018 / 019 Teste N.º 5 Matemática A Duração do Teste (Caderno 1 + Caderno ): 90 minutos 10.º Ano de Escolaridade Nome do aluno: N.º: Turma: Este teste é constituído por dois cadernos:
Teste de Matemática A 018 / 019 Teste N.º 5 Matemática A Duração do Teste (Caderno 1 + Caderno ): 90 minutos 10.º Ano de Escolaridade Nome do aluno: N.º: Turma: Este teste é constituído por dois cadernos:
Ricardo Bianconi. Fevereiro de 2015
 Seções Cônicas Ricardo Bianconi Fevereiro de 2015 Uma parte importante da Geometria Analítica é o estudo das curvas planas e, em particular, das cônicas. Neste texto estudamos algumas propriedades das
Seções Cônicas Ricardo Bianconi Fevereiro de 2015 Uma parte importante da Geometria Analítica é o estudo das curvas planas e, em particular, das cônicas. Neste texto estudamos algumas propriedades das
Geometria Analítica I
 Geom. Analítica I Respostas do Módulo I - Aula 7 1 Geometria Analítica I 01/03/2011 Respostas dos Exercícios do Módulo I - Aula 7 Aula 7 1. a. Procedendo como nos Exemplos 7.1 e 7.2, ou a Proposição 7.15
Geom. Analítica I Respostas do Módulo I - Aula 7 1 Geometria Analítica I 01/03/2011 Respostas dos Exercícios do Módulo I - Aula 7 Aula 7 1. a. Procedendo como nos Exemplos 7.1 e 7.2, ou a Proposição 7.15
Capítulo 19. Coordenadas polares
 Capítulo 19 Coordenadas polares Neste capítulo, veremos que há outra maneira de expressar a posição de um ponto no plano, distinta da forma cartesiana. Embora os sistemas cartesianos sejam muito utilizados,
Capítulo 19 Coordenadas polares Neste capítulo, veremos que há outra maneira de expressar a posição de um ponto no plano, distinta da forma cartesiana. Embora os sistemas cartesianos sejam muito utilizados,
Este trabalho foi licenciado com a Licença Creative Commons Atribuição - NãoComercial - SemDerivados 3.0 Não Adaptada
 1. Introdução Definição: Parábola é o lugar geométrico dos pontos do plano cujas distâncias entre uma reta fixa, chamada de reta diretriz, e a um ponto fixo situado fora desta reta, chamado de foco da
1. Introdução Definição: Parábola é o lugar geométrico dos pontos do plano cujas distâncias entre uma reta fixa, chamada de reta diretriz, e a um ponto fixo situado fora desta reta, chamado de foco da
FICHA de AVALIAÇÃO de MATEMÁTICA A 11.º Ano Versão 1
 FICHA de AVALIAÇÃO de MATEMÁTICA A.º Ano Versão Nome: N.º Turma: Apresente o seu raciocínio de orma clara, indicando todos os cálculos que tiver de eetuar e todas as justiicações necessárias. Quando, para
FICHA de AVALIAÇÃO de MATEMÁTICA A.º Ano Versão Nome: N.º Turma: Apresente o seu raciocínio de orma clara, indicando todos os cálculos que tiver de eetuar e todas as justiicações necessárias. Quando, para
18REV - Revisão. LMAT 3B-2 - Geometria Analítica. Questão 1
 18REV - Revisão LMAT 3B-2 - Geometria Analítica Questão 1 (Unicamp 2017) Seja i a unidade imaginária, isto é, i 2 = 1. O lugar geométrico dos pontos do plano cartesiano com coordenadas reais (x, y) tais
18REV - Revisão LMAT 3B-2 - Geometria Analítica Questão 1 (Unicamp 2017) Seja i a unidade imaginária, isto é, i 2 = 1. O lugar geométrico dos pontos do plano cartesiano com coordenadas reais (x, y) tais
(7) Suponha que sobre uma certa região do espaço o potencial elétrico V é dado por V(x, y, z) = 5x 2 3xy + xyz.
 1. MAT - 0147 CÁLCULO DIFERENCIAL E INTEGRAL II PARA ECÔNOMIA 3 a LISTA DE EXERCÍCIOS - 017 1) Em cada caso, esboce a superfície de nível c da função F : R 3 R: a) Fx, y, z) = x + y + 3z e c = 1 b) Fx,
1. MAT - 0147 CÁLCULO DIFERENCIAL E INTEGRAL II PARA ECÔNOMIA 3 a LISTA DE EXERCÍCIOS - 017 1) Em cada caso, esboce a superfície de nível c da função F : R 3 R: a) Fx, y, z) = x + y + 3z e c = 1 b) Fx,
Capítulo 2. Retas no plano. 1. Retas verticais e não-verticais. Definição 1
 Capítulo 2 Retas no plano O objetivo desta aula é determinar a equação algébrica que representa uma reta no plano. Para isso, vamos analisar separadamente dois tipos de reta: reta vertical e reta não-vertical.
Capítulo 2 Retas no plano O objetivo desta aula é determinar a equação algébrica que representa uma reta no plano. Para isso, vamos analisar separadamente dois tipos de reta: reta vertical e reta não-vertical.
Superfícies Quádricas
 Superfícies Quádricas Jorge M. V. Capela, Marisa V. Capela Instituto de Química - UNESP Araraquara, SP capela@iq.unesp.br Araraquara, SP - 2017 1 Superfícies de Revolução São superfícies criadas pela rotação
Superfícies Quádricas Jorge M. V. Capela, Marisa V. Capela Instituto de Química - UNESP Araraquara, SP capela@iq.unesp.br Araraquara, SP - 2017 1 Superfícies de Revolução São superfícies criadas pela rotação
Aula 18 Multiplicadores de Lagrange. (2 a parte) Objetivo. Usar os multiplicadores de Lagrange para calcular máximos e mínimos.
 Aula 18 Multiplicadores de Lagrange (2 a parte) Objetivo Usar os multiplicadores de Lagrange para calcular máximos e mínimos. Começamos com um exemplo no qual queremos determinar o máximo eomínimo de uma
Aula 18 Multiplicadores de Lagrange (2 a parte) Objetivo Usar os multiplicadores de Lagrange para calcular máximos e mínimos. Começamos com um exemplo no qual queremos determinar o máximo eomínimo de uma
Retas e círculos, posições relativas e distância de um ponto a uma reta
 Capítulo 3 Retas e círculos, posições relativas e distância de um ponto a uma reta Nesta aula vamos caracterizar de forma algébrica a posição relativa de duas retas no plano e de uma reta e de um círculo
Capítulo 3 Retas e círculos, posições relativas e distância de um ponto a uma reta Nesta aula vamos caracterizar de forma algébrica a posição relativa de duas retas no plano e de uma reta e de um círculo
Distância entre duas retas. Regiões no plano
 Capítulo 4 Distância entre duas retas. Regiões no plano Nesta aula, veremos primeiro como podemos determinar a distância entre duas retas paralelas no plano. Para isso, lembramos que, na aula anterior,
Capítulo 4 Distância entre duas retas. Regiões no plano Nesta aula, veremos primeiro como podemos determinar a distância entre duas retas paralelas no plano. Para isso, lembramos que, na aula anterior,
J. Delgado - K. Frensel - L. Crissaff Geometria Analítica e Cálculo Vetorial
 76 Capítulo 4 Distâncias no plano e regiões no plano 1. Distância de um ponto a uma reta Dados um ponto P e uma reta r no plano, já sabemos calcular a distância de P a cada ponto P r. Definição 1 Definimos
76 Capítulo 4 Distâncias no plano e regiões no plano 1. Distância de um ponto a uma reta Dados um ponto P e uma reta r no plano, já sabemos calcular a distância de P a cada ponto P r. Definição 1 Definimos
Equações paramétricas das cônicas
 Aula 1 Equações paramétricas das cônicas Ao estudarmos as retas no plano, vimos que a reta r que passa por dois pontos distintos P 1 = x 1, y 1 ) e P = x, y ) é dada pelas seguintes equações paramétricas:
Aula 1 Equações paramétricas das cônicas Ao estudarmos as retas no plano, vimos que a reta r que passa por dois pontos distintos P 1 = x 1, y 1 ) e P = x, y ) é dada pelas seguintes equações paramétricas:
Aula 17 Máximos e mínimos (2 a parte) Multiplicadores de Lagrange
 Aula 17 Máximos e mínimos (2 a parte) Multiplicadores de Lagrange MÓDULO 1 AULA 17 Ao pedir um conselho, estamos, na maioria das vezes, buscando um cúmplice. Lagrange Objetivo Usar os multiplicadores de
Aula 17 Máximos e mínimos (2 a parte) Multiplicadores de Lagrange MÓDULO 1 AULA 17 Ao pedir um conselho, estamos, na maioria das vezes, buscando um cúmplice. Lagrange Objetivo Usar os multiplicadores de
Lista de exercícios de GA na reta e no plano Período de Prof. Fernando Carneiro Rio de Janeiro, Janeiro de 2017
 Lista de GA no plano 1 Lista de exercícios de GA na reta e no plano Período de 016. - Prof. Fernando Carneiro Rio de Janeiro, Janeiro de 017 1 Retas no plano 1.1) Determine os dois pontos, que chamaremos
Lista de GA no plano 1 Lista de exercícios de GA na reta e no plano Período de 016. - Prof. Fernando Carneiro Rio de Janeiro, Janeiro de 017 1 Retas no plano 1.1) Determine os dois pontos, que chamaremos
Universidade Federal de Mato Grosso do Sul - UFMS VGA - 2 a Prova - Engenharia Civil + Física 03 de Julho de Prof o. E.T.
 Universidade Federal de Mato Grosso do Sul - UFMS VGA - 2 a Prova - Engenharia Civil + Física 0 de Julho de 2014 - Prof o ETGalante 1 (2,0 pontos) Na gura acima ABCDEF GH é um paralelepípedo O ponto M
Universidade Federal de Mato Grosso do Sul - UFMS VGA - 2 a Prova - Engenharia Civil + Física 0 de Julho de 2014 - Prof o ETGalante 1 (2,0 pontos) Na gura acima ABCDEF GH é um paralelepípedo O ponto M
Escola Secundária de Alberto Sampaio Ficha Formativa de Matemática A Geometria IV Paralelismo e perpendicularidade. Sistemas de equações.
 Escola Secundária de Alberto Sampaio Ficha Formativa de Matemática A Geometria IV Paralelismo e perpendicularidade. Sistemas de equações. 11º Ano Paralelismo e perpendicularidade de retas No espaço, duas
Escola Secundária de Alberto Sampaio Ficha Formativa de Matemática A Geometria IV Paralelismo e perpendicularidade. Sistemas de equações. 11º Ano Paralelismo e perpendicularidade de retas No espaço, duas
Posição relativa entre retas e círculos e distâncias
 4 Posição relativa entre retas e círculos e distâncias Sumário 4.1 Distância de um ponto a uma reta.......... 2 4.2 Posição relativa de uma reta e um círculo no plano 4 4.3 Distância entre duas retas no
4 Posição relativa entre retas e círculos e distâncias Sumário 4.1 Distância de um ponto a uma reta.......... 2 4.2 Posição relativa de uma reta e um círculo no plano 4 4.3 Distância entre duas retas no
Geometria Analítica I
 Geom. Analítica I Respostas do Módulo I - Aula 14 1 Geometria Analítica I 10/03/011 Respostas dos Exercícios do Módulo I - Aula 14 Aula 14 1. a. A equação do círculo de centro h, k) e raio r é x h) + y
Geom. Analítica I Respostas do Módulo I - Aula 14 1 Geometria Analítica I 10/03/011 Respostas dos Exercícios do Módulo I - Aula 14 Aula 14 1. a. A equação do círculo de centro h, k) e raio r é x h) + y
d{p, s) = R. Mas, d(p, s) = d(p, Q), onde Q(0, 0, z). Logo, P{x, y, z) pertence ao cilindro se, e somente se,
 134 Geometria Analítica \ Vamos deduzir uma equação do cilindro, em relação a um sistema de coordenadas que contém s como eixo z. Seja R a distância entre r es. Então, um ponto P(x, y, z) pertence ao cilindro
134 Geometria Analítica \ Vamos deduzir uma equação do cilindro, em relação a um sistema de coordenadas que contém s como eixo z. Seja R a distância entre r es. Então, um ponto P(x, y, z) pertence ao cilindro
1. as equações paramétricas da reta que contém o ponto A e é perpendicular ao plano de equação x 2y + 3z = 17;
 PROVA 1 09 de setembro de 2015 08h30 1 2 3 4 5 081 x = 1 + 3t 0811 Considere a reta L de equações paramétricas y = t z = 5 A = (5, 0, 2). Obtenha e o ponto 1. as equações paramétricas da reta que contém
PROVA 1 09 de setembro de 2015 08h30 1 2 3 4 5 081 x = 1 + 3t 0811 Considere a reta L de equações paramétricas y = t z = 5 A = (5, 0, 2). Obtenha e o ponto 1. as equações paramétricas da reta que contém
MAT Poli Cônicas - Parte I
 MAT2454 - Poli - 2011 Cônicas - Parte I Uma equação quadrática em duas variáveis, x e y, é uma equação da forma ax 2 +by 2 +cxy +dx+ey +f = 0, em que pelo menos um doscoeficientes a, b oucénão nulo 1.
MAT2454 - Poli - 2011 Cônicas - Parte I Uma equação quadrática em duas variáveis, x e y, é uma equação da forma ax 2 +by 2 +cxy +dx+ey +f = 0, em que pelo menos um doscoeficientes a, b oucénão nulo 1.
Resumo com exercícios resolvidos dos assuntos:
 www.engenhariafacil.weebly.com (0)- Considerações iniciais: Resumo com exercícios resolvidos dos assuntos: Máximos e mínimos absolutos e Multiplicador de Lagrange -Grande parte das funções não possui máximos
www.engenhariafacil.weebly.com (0)- Considerações iniciais: Resumo com exercícios resolvidos dos assuntos: Máximos e mínimos absolutos e Multiplicador de Lagrange -Grande parte das funções não possui máximos
Universidade Federal do Rio de Janeiro
 Å INSTITUTO DE MATEMÁTICA Universidade Federal do Rio de Janeiro Gabarito da a Prova Unificada de Cálculo I a Questão: Calcule ou justifique caso não exista, cada um dos ite abaixo: ( (a) x + (+x )e x,
Å INSTITUTO DE MATEMÁTICA Universidade Federal do Rio de Janeiro Gabarito da a Prova Unificada de Cálculo I a Questão: Calcule ou justifique caso não exista, cada um dos ite abaixo: ( (a) x + (+x )e x,
Todos os exercícios sugeridos nesta apostila se referem ao volume 3. MATEMÁTICA III 1 ESTUDO DA CIRCUNFERÊNCIA
 DEFINIÇÃO... EQUAÇÃO REDUZIDA... EQUAÇÃO GERAL DA CIRCUNFERÊNCIA... 3 RECONHECIMENTO... 3 POSIÇÃO RELATIVA ENTRE PONTO E CIRCUNFERÊNCIA... 1 POSIÇÃO RELATIVA ENTRE RETA E CIRCUNFERÊNCIA... 17 PROBLEMAS
DEFINIÇÃO... EQUAÇÃO REDUZIDA... EQUAÇÃO GERAL DA CIRCUNFERÊNCIA... 3 RECONHECIMENTO... 3 POSIÇÃO RELATIVA ENTRE PONTO E CIRCUNFERÊNCIA... 1 POSIÇÃO RELATIVA ENTRE RETA E CIRCUNFERÊNCIA... 17 PROBLEMAS
(x,y) x Exemplo: (x, y) ou f x. x = f x = 2xy. y = f y
 1 DEFINIÇÃO DE Chamamos de derivada parcial quando temos uma função que envolve mais de uma variável e queremos derivar em relação a uma delas. De forma geral, basta derivarmos em relação à variável de
1 DEFINIÇÃO DE Chamamos de derivada parcial quando temos uma função que envolve mais de uma variável e queremos derivar em relação a uma delas. De forma geral, basta derivarmos em relação à variável de
7 a lista de exercícios - GA Período de Prof. Fernando Carneiro
 Lista 7 de GA 1 7 a lista de exercícios - GA Período de 014. - Prof. Fernando Carneiro 1 (Boulos): Dados os pontos A(1, 0, 0), B(, 1, 0), C(1, 0, 1) e D(, 1, 1), mostre que a) formam um retângulo; b) a
Lista 7 de GA 1 7 a lista de exercícios - GA Período de 014. - Prof. Fernando Carneiro 1 (Boulos): Dados os pontos A(1, 0, 0), B(, 1, 0), C(1, 0, 1) e D(, 1, 1), mostre que a) formam um retângulo; b) a
Universidade Federal de Mato Grosso do Sul - UFMS VGA - 2 a Prova - Engenharia de Computação 03 de Julho de Prof o. E.T.
 Universidade Federal de Mato Grosso do Sul - UFMS VGA - 2 a Prova - Engenharia de Computação 0 de Julho de 2014 - Prof o ETGalante 1 (2,0 pontos) Na gura acima ABCDEF GH é um paralelepípedo O ponto M é
Universidade Federal de Mato Grosso do Sul - UFMS VGA - 2 a Prova - Engenharia de Computação 0 de Julho de 2014 - Prof o ETGalante 1 (2,0 pontos) Na gura acima ABCDEF GH é um paralelepípedo O ponto M é
Notas de Aulas 3 - Cônicas Prof Carlos A S Soares
 Notas de Aulas 3 - Cônicas Prof Carlos A S Soares 1 Parábolas 11 Conceito e Elementos Definição 1 Sejam l uma reta e F um ponto não pertencente a l Chamamos parábola de diretriz l e foco F o conjunto dos
Notas de Aulas 3 - Cônicas Prof Carlos A S Soares 1 Parábolas 11 Conceito e Elementos Definição 1 Sejam l uma reta e F um ponto não pertencente a l Chamamos parábola de diretriz l e foco F o conjunto dos
GAAL /1 - Simulado - 2 produto escalar, produto vetorial, retas e planos. Exercício 1: Determine a equação do plano em cada situação descrita.
 GAAL - 2013/1 - Simulado - 2 produto escalar, produto vetorial, retas e planos SOLUÇÕES Exercício 1: Determine a equação do plano em cada situação descrita. (a) O plano passa pelo ponto A = (2, 0, 2) e
GAAL - 2013/1 - Simulado - 2 produto escalar, produto vetorial, retas e planos SOLUÇÕES Exercício 1: Determine a equação do plano em cada situação descrita. (a) O plano passa pelo ponto A = (2, 0, 2) e
