Aplicações à Física e à Engenharia
|
|
|
- Matilde Rijo Bergmann
- 6 Há anos
- Visualizações:
Transcrição
1 UNIVERSIDADE DO ESTADO DE MATO GROSSO CAMPUS UNIVERSITÁRIO DE SINOP FACULDADE DE CIÊNCIAS EXATAS E TECNOLÓGICAS CURSO DE ENGENHARIA CIVIL DISCIPLINA: CÁLCULO DIFERENCIAL E INTEGRAL I Aplicações à Física e à Engenharia Prof.: Rogério Dias Dalla Riva
2 Aplicações à Física e à Engenharia 1.Introdução 2.Pressão Hidrostática e Força 3.Resolução de Exemplos 4.Momentos e Centros de Massa 5.Resolução de Exemplos
3 1. Introdução Junto com as muitas aplicações de cálculo integral à Física e à Engenharia consideramos duas aqui: a força devido à pressão da água e centros de massa. Como em nossas aplicações anteriores à geometrica (áreas, volume e comprimentos) e ao trabalho, nossa estratégia é quebrar a quantidade física em um grande número de pequenas partes, aproximar cada pequena parte, adicionar os resultados, tomar o limite e então avaliar a integral resultante. 3
4 2. Pressão hidrostática e força Os mergulhadores notam que a pressão da água aumenta quando eles mergulham mais profundamente. Isso ocorre por causa do aumento do peso da água acima deles. 4
5 2. Pressão hidrostática e força Em geral, suponha que uma placa horizontal fina com a área A por metros quadrados seja submersa em um fluido de densidade ρ quilogramas por metro cúbico a uma profundidade d metros abaixo da superfície do fluido, como na figura abaixo. 5
6 2. Pressão hidrostática e força O fluido diretamente acima da placa tem um volume V = Ad, assim sua massa é m = ρv = ρad. A força exercida pelo fluido na placa é, portanto: F = mg = ρgad onde g é a aceleração da gravidade. A pressão P na placa é definida como a força por unidade de área: P F = = ρgd A 6
7 2. Pressão hidrostática e força No Sistema Internacional de Unidades, a pressão é medida em newtons por metro quadrado, que é chamada pascal (1 N/m 2 = 1 Pa). Como essa é uma unidade pequena, o kilopascal (kpa) é frequentemente usado. Por exemplo, uma vez que a densidade da água é de ρ = kg/m 3, a pressão no fundo de uma piscina de 2 m de profundidade é P = ρgd = kg/m 9,8 m/s 2 m P = Pa = 19,6 kpa 7
8 2. Pressão hidrostática e força Um princípio importante da pressão de fluidos é o fato verificado experimentalmente de que em qualquer ponto no líquido a pressão é a mesma em todas as direções. Então, a pressão em qualquer direção a uma profundidade d em um fluido com densidade ρ é dada por P = ρgd = δd 8
9 2. Pressão hidrostática e força Isso nos ajuda a determinar a força hidrostática contra uma placa vertical ou parede de uma represa em um fluido. Este não é um problema simples, porque a pressão não é constante, mas se eleva com o aumento da profundidade. 9
10 3. Resolução de exemplos Exemplo 1: Uma represa tem o formato do trapézio mostrado na figura a seguir. A altura é de 20 m, e a largura é de 50 m no topo e 30 m no fundo. Clacule a força na represa devido à pressão hidrostática da água se o nível da água está a 4 m do topo da represa. 10
11 3. Resolução de exemplos Solução: Escolhemos um eixo vertical x com origem na superfície da água, como na figura a seguir. 11
12 3. Resolução de exemplos A profundidade da água é de 16 m; assim, dividimos o intervalo [0, 16] em subintervalos de igual comprimento com extremos x i e x i * [x i-1, x i ]. A i-ésima faixa horizontal da represa é aproximada por um retângulo com altura x e largura w i, onde, por similaridade de triângulos (ver figura abaixo) a 10 1 x = = * 16 i x x a = = * * i i 12
13 3. Resolução de exemplos e assim 1 w = 2 (15 + a) = 2 ( x ) = 46 x 2 * * i i i Se A i é a área da i-ésima, então A = w x = x x * i i (46 i ) 13
14 3. Resolução de exemplos Se x é pequena, então a pressão P i na i-ésima faixa é praticamente constante, e podemos escrever P i ,8 x * i P i x * i 14
15 3. Resolução de exemplos A força hidrostática F i agindo na i-ésima faixa é o produto da pressão pela área: F = P A x x x * * i i i i (46 i ) Adicionando essas forças e tomando o limite quando n, obtemos a força hidrostática total na represa: n * * i lim i (46 i ) n i = 1 F = x x x 15
16 3. Resolução de exemplos F 16 F = x (46 x) dx (46 ) F = x x dx x F = x = ,43 10 N
17 3. Resolução de exemplos Exemplo 2: Calcule a força hidrostática no extremo de um tambor cilíndrico com raio de 3 pés que está submerso em água com 10 pés de profundidade. Considere δ = 62,5 lb/pés 2. 17
18 3. Resolução de exemplos Solução: Neste exemplo é conveniente escolher os eixos como na figura abaixo, de modo que a origem seja colocada no centro do tambor. 3 18
19 3. Resolução de exemplos Então o círculo tem uma equação simples x 2 + y 2 = 9. Como no Exemplo 1, dividimos a região circular em faixas horizontais de larguras iguais. Da equação do círculo, vemos que o comprimento da i-ésima faixa é e assim sua área é ( * y ) i ( * ) 2 i A = 2 9 y y i 19
20 3. Resolução de exemplos A pressão nessa faixa é aproximadamente δd i ( * y ) i = 62,5 7 e assim a força na faixa é aproximadamente ( * ) ( * ) 2 δd A = 62,5 7 y 2 9 y y i i i i 20
21 3. Resolução de exemplos A força total é obtida pela soma das forças em todas as faixas e tomando-se o limite n n i = 1 ( * ) ( * ) 2 i i F = lim 62,5 7 y 2 9 y y 3 2 F y 9 y dy 3 ( ) = F y dy 125 y 9 y dy =
22 3. Resolução de exemplos A segunda integral é 0, porque o integrando é uma função ímpar [f(-y) = -f(y)]. Portanto: F 3 = Lembrando que 3 2 y dy u a sin u a u du = a u + + C 2 2 a 22
23 3. Resolução de exemplos Teremos F y y F = y + sin ( 3) 9 1 ( 3) = sin 9 9 sin F 9 9 = sin (1) sin ( 1) 9 π 9 π 9π F = 875 = lb
24 3. Resolução de exemplos Outra forma de resolver o Exemplo 2 é observar que a área a ser determinada corresponde à área de um disco semicircular de raio 3. Portanto: F π 2 2 r π (3) = 875 = lb
25 4. Momentos e centros de massa Nosso principal objetivo aqui é encontrar o ponto P no qual uma fina placa de qualquer formato se equilibra horizontalmente, como na figura a seguir. Esse ponto é chamado centro de massa (ou centro de gravidade) da placa. 25
26 4. Momentos e centros de massa Primeiro consideramos a situação mais simples mostrada na figura abaixo, onde duas massas m 1 e m 2 são presas a um bastão de massa desprezível em lados opostos a um apoio e a distâncias d 1 e d 2 do apoio. 26
27 4. Momentos e centros de massa O eixo ficará em equilíbrio se m d = m d Esse é um fato experimental descoberto por Arquimedes e chamado Lei da Alavanca. 27
28 4. Momentos e centros de massa Agora suponha que o eixo esteja sobre o eixo x com m 1 em x 1 e m 2 em x 2 e o centro de massa em. Se verificarmos a figura abaixo, veremos que d = x x e d = x x
29 4. Momentos e centros de massa Portanto m d = m d ( ) = ( ) m x x m x x m1x m1x 1 = m2x2 m2x m1x + m2x = m1x 1 + m2x2 ( ) x m + m = m x + m x x = m x m + m x + m
30 4. Momentos e centros de massa Os números m 1 x 1 e m 2 x 2 são denominados momentos das massas m 1 e m 2 (em relação à origem) e a equação anterior diz que o centro de massa é obtido pela soma dos momentos das massas e divisão pela massa total m = m 1 + m 2. 30
31 4. Momentos e centros de massa Em geral, temos um sistema de n partículas com massas m 1 m 2,, m n localizadas nos pontos x 1, x 2,, x n sobre o eixo x. Podemos mostrar similarmente que o centro de massa do sistema está localizado em n n = = = m x m x x m m i i i i n i = 1 i = 1 n mi m i = 1 i = 1 i 31
32 4. Momentos e centros de massa onde m é a massa total do sistema, e a soma dos momentos individuais M n = i = 1 m x i i é chamada momento do sistema em relação à origem. Então pode ser reescrita como mx = que diz que se a massa total fosse considerada como concentrada no centro de massa, então seu momento deveria ser o mesmo que o momento do sistema. M 32
33 4. Momentos e centros de massa Agora considere um sistema de n partículas com massas m 1 m 2,, m n nos pontos (x 1, y 1 ), (x 2, y 2 ),, (x n, y n ) no plano xy como mostrado na figura abaixo 33
34 4. Momentos e centros de massa Por analogia com o caso unidimensional, definimos o momento do sistema com relação ao eixo y como M n = m x y i i i = 1 e o momento do sistema com relação ao eixo x como M n = m y x i i i = 1 34
35 4. Momentos e centros de massa Então M y mede a tendência do sistema girar ao redor do eixo y e M x mede a tendência de ele girar ao redor do eixo x. Como no caso unidimensional, as coordenadas (, ) do centro de massa são dadas em termos dos momentos pelas fórmulas x M y = y = m M m x 35
36 4. Momentos e centros de massa onde m = m i é a massa total. Como mx = M e my = M y o centro de massa (, ) é o ponto onde uma partícula única de massa m teria os mesmos momentos do sistema. x 36
37 Exemplo 3: Calcule os momentos e os centros de massa do sistema de objetos que têm massa 3, 4 e 8 nos pontos (-1, 1), (2, -1) e (3, 2). M = 3 ( 1) + 4 (2) + 8 (3) = 29 y M = 3 (1) + 4 ( 1) + 8 (2) = 15 x 37
38 Como m = = 15, obtemos x M y = = m y = =
39 29,1 15 Então o centro de massa é. 39
40 A seguir consideramos uma placa plana (denominada lâmina) com densidade uniforme ρ que ocupa uma regiãor do plano. Desejamos encontrar o centro de massa da placa, chamada centróide (ou centro geométrico) der. Fazendo isso usamos os seguintes princípios físicos: o princípio da simetria diz que se R é simétrico ao redor da reta l, então o centróide de R está em l. 40
41 Simetria em relação ao eixo y R Simetria em relação ao eixo x O centróide de um retângulo é o seu centro 41
42 Os momentos devem ser definidos de maneira que se a massa total da região está concentrada no centro de massa, então seus momentos permanecem inalterados. Também, o momento da união de duas regiões sem a interseção deve ser a soma dos momentos das regiões individuais. 42
43 Suponha que a região R seja do tipo mostrado na figura abaixo; isto é, R esteja entre as retas x = a e x = b, acima do eixo x e abaixo do gráfico de f, onde f é uma função contínua. 43
44 Dividimos o intervalo [a, b] em n subintervalos com os extremos x 0, x 1,, x n e larguras iguais a x. Escolhemos o ponto de amostragem x i* como o ponto médio i do i-ésimo subintervalo, que é i = (x i-1 + x i )/2. Isso determina uma aproximação poligonal a R, mostrada na figura a seguir. 44
45 O centróide do i-ésimo retângulo aproximador R i é seu centro C i ( i, ½f[ i ]). 45
46 Sua área é A = f ( x ) x Assim, sua massa é m = ρf ( x ) x O momento de R i ao redor do eixo y é o produto de sua massa pela distância de C i ao eixo y, que é i. Então i i M ( R ) = [ ρf ( x ) x] x = ρx f ( x ) x y i i i i i 46
47 Somando esses momentos, obtemos o momento da aproximação poligonal a R e, então, tomando o limite quando n, obtemos o momento do própriorem relação ao eixo y. n b M = lim ρx f ( x ) x = ρ xf ( x) dx y i i n i = 1 a 47
48 De maneira similar calculamos o momento de R i em relação ao eixo x como o produto de sua massa e da distância de C i ao eixo x: Mx( Ri ) = [ ρf ( xi ) x] f ( xi ) = ρ [ f ( xi ) ] x 2 2 Novamente somamos esses momentos e tomamos o limite para obter o momento de R ao redor do eixo x. n b x = lim ρ [ ( i ) ] = ρ [ ( i ) ] n i = a M f x x f x dx 48
49 Como no caso do sistema de partículas, o centro de massa da placa é definido de maneira que mx = M e my = M y Mas a massa da placa é o produto de sua densidade por sua área: m = ρa = ρ f ( x) dx b a x 49
50 e assim x b ρ xf ( x) dx xf ( x) dx My a a = = = b b m ρ f ( x) dx f ( x) dx a b a y b b 2 2 ρ Mx a a = = = b b m 1 1 [ f ( x)] dx [ f ( x)] dx 2 2 ρ f ( x) dx f ( x) dx a a 50
51 Note o cancelamento de ρ. A localização do centro de massa independe da densidade. Em resumo, o centro de massa da placa (ou o centróide de R) está localizado no ponto (, ), onde b b x xf ( x) dx y [ f ( x)] dx = = A a A a 2 51
52 Exemplo 4: Calcule o centro de massa de uma placa semicircular de raio r. 52
53 Solução: Para usarmos as fórmulas anteriores, colocamos o semicírculo como na figura abaixo de modo que f ( x) = r x a = r b = r
54 Aqui não há a necessidade de usar a fórmula para calcular porque, pelo princípio da simetria, o centro de massa deve estar sobre o eixo y, e, dessa forma, = 0. A área do semicírculo é A = πr
55 1 1 y = [ f ( x )] dx A 2 Portanto: 2 r b a ( ) y = r 2 x 2 dx = ( r 2 x 2 ) dx 2 2 πr 2 πr 2 r r 2 r r r 3 ( 2 2 ) ( 2 2 ) 2 x r x dx r x dx r x r = = = πr πr πr r 2 2r 4r = 2 r = = 2 πr 3 πr 3 3π r 55
56 O centro de massa está localizado no ponto de coordenadas 4r 0, 3 π 56
57 Exemplo 5: Determine o centróide da região limitada pelas curvas y = cos x, y = 0, x = 0 e x = π/2. 57
58 Solução: A área da região é π 2 ] π 2 = = = 0 0 A cos x dx sen x 1 58
59 π 2 1 x = x cos x dx A 0 Lembrando que u dv = uv v du fazemos u = x du = dx e dv = cos x v = sen x. π 2 π 2 π 2 1 x = x cos x dx = x sen x] sen x dx A π [ ] π 2 π [ ] π 2 π x x = cos = + cos = 1 59
60 π [ ] 2 y = f ( x ) dx A 2 π 2 π 2 π x cos 2 1 = cos ( 1 cos 2 ) 2 x dx = dx x dx 2 = π π π = x sen2x 4 + = =
61 O centróide está localizado no ponto de coordenadas π π 1,
62 Se a regiãorestá entre as curvas y = f(x) e y = g(x), onde f(x) g(x), como mostrado na figura a seguir, então o mesmo tipo de argumento que nos levou às fórmulas para a determinação do centro de massa pode ser usado para mostrar que o centróide deré(, ). 62
63 b x = x[ f ( x) g( x) ] dx y = {[ f ( x)] 2 g( x)] 2 } dx A A 2 a b a 63
64 Exemplo 6: Determine o centróide da região limitada pela reta y = x e a parábola y = x 2. 64
65 Solução: A região é esboçada na figura abaixo. Tomamos f(x) = x, g(x) = x 2, a = 0 e b = 1 na fórmula anterior. 65
66 Cálculo da área: ( 2 ) x x A = x x dx = = =
67 b 1 x = x[ f ( x) g( x) ] dx A a ( 2 ) ( 2 3 x = 6 ) 1 x x x dx = x x dx x x x = 6 = = =
68 b 1 1 { 2 2 y = [ f ( x )] g ( x )] } dx A 2 a ( 2 4 ) 1 ( 2 4 y = 6 ) 1 x x dx = x x dx y x x = 3 = = =
69 O centróide está localizado no ponto de coordenadas 1 2,
70 Agora mostraremos uma conexão entre centróides e volumes de revolução. Teorema de Pappus*: Seja R uma região plana que está inteiramente de um lado de uma reta l em um plano. Se R é girada ao redor de l, então o volume do sólido resultante é o produto da área A de R e a distância d percorrida pelo centróide de R. * Esse teorema tem o nome do matemático grego Pappus de Alexandria, que viveu no século IV. 70
71 Prova: Provaremos para o caso especial no qual a região está entre y = f(x) e y = g(x) como na figura abaixo e a reta l é o eixo y. 71
72 b [ ] V = 2 π x f ( x) g( x) dx a b 2 π x f ( x) g( x) dx = 2π xa = 2π x A = Ad a [ ] ( ) ( ) onde d = 2π é a distância percorrida pelo centróide durante uma rotação ao redor do eixo y. 72
73 Exemplo 7: Um toro é formado pela rotação de um círculo de raio r ao redor de uma reta no plano do círculo que está a uma distância R (> r) do centro do círculo. Calcule o volume do toro. 73
74 Solução: O círculo tem a área A = πr 2. Pelo princípio de simetria, seu centróide é seu centro e, assim, a distância percorrida pelo centróide durante a rotação é d = 2πR. R r 74
75 Portanto, pelo Teorema de Pappus, o volume do toro é ( ) ( ) V = πr 2π R = 2π r R 75
CÁLCULO I. 1 Área de Superfície de Revolução
 CÁLCULO I Prof. Edilson Neri Júnior Prof. André Almeida Aula n o 6: Área de Superfície de Revolução e Pressão Hidrostática Objetivos da Aula Calcular a área de superfícies de revolução; Denir pressão hidrostática.
CÁLCULO I Prof. Edilson Neri Júnior Prof. André Almeida Aula n o 6: Área de Superfície de Revolução e Pressão Hidrostática Objetivos da Aula Calcular a área de superfícies de revolução; Denir pressão hidrostática.
CÁLCULO I Aula 26: Área de Superfície de Revolução e Pressão
 CÁLCULO I Aula 26: Área de e Pressão Prof. Edilson Neri Júnior Prof. André Almeida Universidade Federal do Pará 1 Área de 2 Uma superfície de revolução é um superfície gerada pela rotação de uma curva
CÁLCULO I Aula 26: Área de e Pressão Prof. Edilson Neri Júnior Prof. André Almeida Universidade Federal do Pará 1 Área de 2 Uma superfície de revolução é um superfície gerada pela rotação de uma curva
Trabalho. 1.Introdução 2.Resolução de Exemplos
 UNIVERSIDADE DO ESTADO DE MATO GROSSO CAMPUS UNIVERSITÁRIO DE SINOP FACULDADE DE CIÊNCIAS EXATAS E TECNOLÓGICAS CURSO DE ENGENHARIA CIVIL DISCIPLINA: CÁLCULO DIFERENCIAL E INTEGRAL I Trabalho Prof.: Rogério
UNIVERSIDADE DO ESTADO DE MATO GROSSO CAMPUS UNIVERSITÁRIO DE SINOP FACULDADE DE CIÊNCIAS EXATAS E TECNOLÓGICAS CURSO DE ENGENHARIA CIVIL DISCIPLINA: CÁLCULO DIFERENCIAL E INTEGRAL I Trabalho Prof.: Rogério
CÁLCULO I. Denir o trabalho realizado por uma força variável. Denir pressão e força exercidas por um uido.
 CÁLCULO I Prof. Marcos Diniz Prof. André Almeida Prof. Edilson Neri Júnior Aula n o 3: Aplicações da Integral: Comprimento de Arco. Trabalho. Pressão e Força Hidrostática. Objetivos da Aula Denir comprimento
CÁLCULO I Prof. Marcos Diniz Prof. André Almeida Prof. Edilson Neri Júnior Aula n o 3: Aplicações da Integral: Comprimento de Arco. Trabalho. Pressão e Força Hidrostática. Objetivos da Aula Denir comprimento
Área de uma Superfície de Revolução
 UNIVERSIDADE DO ESTADO DE MATO GROSSO CAMPUS UNIVERSITÁRIO DE SINOP FACULDADE DE CIÊNCIAS EXATAS E TECNOLÓGICAS CURSO DE ENGENHARIA CIVIL DISCIPLINA: CÁLCULO DIFERENCIAL E INTEGRAL I Área de uma Superfície
UNIVERSIDADE DO ESTADO DE MATO GROSSO CAMPUS UNIVERSITÁRIO DE SINOP FACULDADE DE CIÊNCIAS EXATAS E TECNOLÓGICAS CURSO DE ENGENHARIA CIVIL DISCIPLINA: CÁLCULO DIFERENCIAL E INTEGRAL I Área de uma Superfície
Cálculo de Volumes por Cascas Cilíndricas
 UNIVERSIDADE DO ESTADO DE MATO GROSSO CAMPUS UNIVERSITÁRIO DE SINOP FACULDADE DE CIÊNCIAS EXATAS E TECNOLÓGICAS CURSO DE ENGENHARIA CIVIL DISCIPLINA: CÁLCULO DIFERENCIAL E INTEGRAL I Cálculo de Volumes
UNIVERSIDADE DO ESTADO DE MATO GROSSO CAMPUS UNIVERSITÁRIO DE SINOP FACULDADE DE CIÊNCIAS EXATAS E TECNOLÓGICAS CURSO DE ENGENHARIA CIVIL DISCIPLINA: CÁLCULO DIFERENCIAL E INTEGRAL I Cálculo de Volumes
Volumes de Sólidos de Revolução
 UNIVERSIDADE DO ESTADO DE MATO GROSSO CAMPUS UNIVERSITÁRIO DE SINOP FACULDADE DE CIÊNCIAS EXATAS E TECNOLÓGICAS CURSO DE ENGENHARIA CIVIL DISCIPLINA: CÁLCULO DIFERENCIAL E INTEGRAL I Volumes de Sólidos
UNIVERSIDADE DO ESTADO DE MATO GROSSO CAMPUS UNIVERSITÁRIO DE SINOP FACULDADE DE CIÊNCIAS EXATAS E TECNOLÓGICAS CURSO DE ENGENHARIA CIVIL DISCIPLINA: CÁLCULO DIFERENCIAL E INTEGRAL I Volumes de Sólidos
Área e Teorema Fundamental do Cálculo
 UNIVERSIDADE DO ESTADO DE MATO GROSSO CAMPUS UNIVERSITÁRIO DE SINOP FACULDADE DE CIÊNCIAS EXATAS E TECNOLÓGICAS CURSO DE ENGENHARIA CIVIL DISCIPLINA: CÁLCULO DIFERENCIAL E INTEGRAL I Área e Teorema Fundamental
UNIVERSIDADE DO ESTADO DE MATO GROSSO CAMPUS UNIVERSITÁRIO DE SINOP FACULDADE DE CIÊNCIAS EXATAS E TECNOLÓGICAS CURSO DE ENGENHARIA CIVIL DISCIPLINA: CÁLCULO DIFERENCIAL E INTEGRAL I Área e Teorema Fundamental
Aula 14 Áreas entre duas curvas. Volumes e Áreas de sólidos de revolução.
 Universidade Federal do ABC Aula 14 Áreas entre duas curvas. Volumes e Áreas de sólidos de revolução. BCN0402-15 FUV Suporte ao aluno Site da disciplina: http://gradmat.ufabc.edu.br/disciplinas/fuv/ Site
Universidade Federal do ABC Aula 14 Áreas entre duas curvas. Volumes e Áreas de sólidos de revolução. BCN0402-15 FUV Suporte ao aluno Site da disciplina: http://gradmat.ufabc.edu.br/disciplinas/fuv/ Site
Aplicações de. Integração
 Aplicações de Capítulo 6 Integração APLICAÇÕES DE INTEGRAÇÃO Neste capítulo exploraremos algumas das aplicações da integral definida, utilizando-a para calcular áreas entre curvas, volumes de sólidos e
Aplicações de Capítulo 6 Integração APLICAÇÕES DE INTEGRAÇÃO Neste capítulo exploraremos algumas das aplicações da integral definida, utilizando-a para calcular áreas entre curvas, volumes de sólidos e
Comprimento de Arco. 1.Introdução 2.Resolução de Exemplos 3.Função Comprimento de Arco 4.Resolução de Exemplo
 UNIVERSIDADE DO ESTADO DE MATO GROSSO CAMPUS UNIVERSITÁRIO DE SINOP FACULDADE DE CIÊNCIAS EXATAS E TECNOLÓGICAS CURSO DE ENGENHARIA CIVIL DISCIPLINA: CÁLCULO DIFERENCIAL E INTEGRAL I Comprimento de Arco
UNIVERSIDADE DO ESTADO DE MATO GROSSO CAMPUS UNIVERSITÁRIO DE SINOP FACULDADE DE CIÊNCIAS EXATAS E TECNOLÓGICAS CURSO DE ENGENHARIA CIVIL DISCIPLINA: CÁLCULO DIFERENCIAL E INTEGRAL I Comprimento de Arco
Integração Volume. Aula 07 Matemática II Agronomia Prof. Danilene Donin Berticelli
 Integração Volume Aula 7 Matemática II Agronomia Prof. Danilene Donin Berticelli Volume de um sólido Na tentativa de encontra o volume de um sólido, nos deparamos com o mesmo tipo de problema que para
Integração Volume Aula 7 Matemática II Agronomia Prof. Danilene Donin Berticelli Volume de um sólido Na tentativa de encontra o volume de um sólido, nos deparamos com o mesmo tipo de problema que para
9 ạ Lista de Exercícios de Cálculo II Integrais Triplas: Coordenadas Retangulares, Cilíndricas e Esféricas; Mudança de Variáveis
 9 ạ Lista de Exercícios de Cálculo II Integrais Triplas: Coordenadas Retangulares, Cilíndricas e Esféricas; Mudança de Variáveis Professora: Michelle Pierri Exercício 1 Encontre o volume do sólido limitado
9 ạ Lista de Exercícios de Cálculo II Integrais Triplas: Coordenadas Retangulares, Cilíndricas e Esféricas; Mudança de Variáveis Professora: Michelle Pierri Exercício 1 Encontre o volume do sólido limitado
6.3. Cálculo de Volumes por Cascas Cilíndricas
 APLICAÇÕES DE INTEGRAÇÃO 6.3 Cálculo de Volumes por Cascas Cilíndricas Nesta seção aprenderemos como aplicar o método das cascas cilíndricas para encontrar o volume de um sólido. VOLUMES POR CASCAS CILÍNDRICAS
APLICAÇÕES DE INTEGRAÇÃO 6.3 Cálculo de Volumes por Cascas Cilíndricas Nesta seção aprenderemos como aplicar o método das cascas cilíndricas para encontrar o volume de um sólido. VOLUMES POR CASCAS CILÍNDRICAS
Integrais - Aplicações I. Daniel 26 de novembro de 2016
 Integrais - Aplicações I Daniel 26 de novembro de 2016 1 Sumário Aplicações da Integral Construção de Fórmulas Integrais Aplicação da Estratégia de Integrais Definidas Áreas entre duas Curvas Volume por
Integrais - Aplicações I Daniel 26 de novembro de 2016 1 Sumário Aplicações da Integral Construção de Fórmulas Integrais Aplicação da Estratégia de Integrais Definidas Áreas entre duas Curvas Volume por
Figura 1. Duas partículas de diferentes massas perfeitamente apoiadas pelo bastão = (1)
 PRÁTICA 13: CENTRO DE MASSA Centro de massa (ou centro de gravidade) de um objeto pode ser definido como o ponto em que ele pode ser equilibrado horizontalmente. Seu significado físico tem muita utilidade
PRÁTICA 13: CENTRO DE MASSA Centro de massa (ou centro de gravidade) de um objeto pode ser definido como o ponto em que ele pode ser equilibrado horizontalmente. Seu significado físico tem muita utilidade
Integrais - Aplicações I
 Integrais - Aplicações I Daniel 17 de novembro de 2015 Daniel Integrais - Aplicações I 17 de novembro de 2015 1 / 45 Áreas entre duas Curvas Sumário 1 Áreas entre duas Curvas 2 Volume por Seções Transversais
Integrais - Aplicações I Daniel 17 de novembro de 2015 Daniel Integrais - Aplicações I 17 de novembro de 2015 1 / 45 Áreas entre duas Curvas Sumário 1 Áreas entre duas Curvas 2 Volume por Seções Transversais
Integrais - Aplicações I
 Integrais - Aplicações I Daniel 13 de novembro de 2015 Daniel Integrais - Aplicações I 13 de novembro de 2015 1 / 37 Áreas entre duas Curvas Área entre duas curvas Se f e g são funções integráveis em [a,b]
Integrais - Aplicações I Daniel 13 de novembro de 2015 Daniel Integrais - Aplicações I 13 de novembro de 2015 1 / 37 Áreas entre duas Curvas Área entre duas curvas Se f e g são funções integráveis em [a,b]
Aula 32. Alexandre Nolasco de Carvalho Universidade de São Paulo São Carlos SP, Brazil
 Superfícies de Revolução e Outras Aplicações Aula 32 Alexandre Nolasco de Carvalho Universidade de São Paulo São Carlos SP, Brazil 29 de Maio de 2014 Primeiro Semestre de 2014 Turma 2014106 - Engenharia
Superfícies de Revolução e Outras Aplicações Aula 32 Alexandre Nolasco de Carvalho Universidade de São Paulo São Carlos SP, Brazil 29 de Maio de 2014 Primeiro Semestre de 2014 Turma 2014106 - Engenharia
Aplicação de Integral Definida: Volumes de Sólidos de Revolução
 Aplicação de Integral Definida: Prof a. Sólidos Exemplos de Sólidos: esfera, cone circular reto, cubo, cilindro. Sólidos de Revolução são sólidos gerados a partir da rotação de uma área plana em torno
Aplicação de Integral Definida: Prof a. Sólidos Exemplos de Sólidos: esfera, cone circular reto, cubo, cilindro. Sólidos de Revolução são sólidos gerados a partir da rotação de uma área plana em torno
Integrais - Aplicações I
 Integrais - Aplicações I Daniel 13 de novembro de 2015 Daniel Integrais - Aplicações I 13 de novembro de 2015 1 / 33 Áreas entre duas Curvas Área entre duas curvas Se f e g são funções integráveis em [a,b]
Integrais - Aplicações I Daniel 13 de novembro de 2015 Daniel Integrais - Aplicações I 13 de novembro de 2015 1 / 33 Áreas entre duas Curvas Área entre duas curvas Se f e g são funções integráveis em [a,b]
CÁLCULO I. 1 Área entre Curvas. Objetivos da Aula. Aula n o 28: Área entre Curvas, Comprimento de Arco e Trabalho. Calcular área entre curvas;
 CÁLCULO I Prof. Marcos Diniz Prof. Edilson Neri Júnior Prof. André Almeida Aula n o 8: Área entre Curvas, Comprimento de Arco e Trabalho Objetivos da Aula Calcular área entre curvas; Calcular o comprimento
CÁLCULO I Prof. Marcos Diniz Prof. Edilson Neri Júnior Prof. André Almeida Aula n o 8: Área entre Curvas, Comprimento de Arco e Trabalho Objetivos da Aula Calcular área entre curvas; Calcular o comprimento
QUESTÕES DE CÁLCULO (2) = 2 ( ) = 1. O valor do limite L = lim se encontra no intervalo:
 1. O valor do limite L = lim se encontra no intervalo: a) 0 L 1 b) 1 L c) L 3 d) 3 L 4 e) L 4. A função f(x) é continua em x= quando f() vale: = + 3 10 () = a) - b) -5 c) d) 5 e) 7 3. A derivada da função
1. O valor do limite L = lim se encontra no intervalo: a) 0 L 1 b) 1 L c) L 3 d) 3 L 4 e) L 4. A função f(x) é continua em x= quando f() vale: = + 3 10 () = a) - b) -5 c) d) 5 e) 7 3. A derivada da função
O centróide de área é definido como sendo o ponto correspondente ao centro de gravidade de uma placa de espessura infinitesimal.
 CENTRÓIDES E MOMENTO DE INÉRCIA Centróide O centróide de área é definido como sendo o ponto correspondente ao centro de gravidade de uma placa de espessura infinitesimal. De uma maneira bem simples: centróide
CENTRÓIDES E MOMENTO DE INÉRCIA Centróide O centróide de área é definido como sendo o ponto correspondente ao centro de gravidade de uma placa de espessura infinitesimal. De uma maneira bem simples: centróide
Medida de Ângulos em Radianos
 UNIVERSIDADE DO ESTADO DE MATO GROSSO CAMPUS UNIVERSITÁRIO DE SINOP FACULDADE DE CIÊNCIAS EXATAS E TECNOLÓGICAS CURSO DE ENGENHARIA CIVIL DISCIPLINA: CÁLCULO DIFERENCIAL E INTEGRAL I Medida de Ângulos
UNIVERSIDADE DO ESTADO DE MATO GROSSO CAMPUS UNIVERSITÁRIO DE SINOP FACULDADE DE CIÊNCIAS EXATAS E TECNOLÓGICAS CURSO DE ENGENHARIA CIVIL DISCIPLINA: CÁLCULO DIFERENCIAL E INTEGRAL I Medida de Ângulos
Aula 33. Alexandre Nolasco de Carvalho Universidade de São Paulo São Carlos SP, Brazil
 Aplicações da Integral - Continuação e Técnicas de Integração Aula 33 Alexandre Nolasco de Carvalho Universidade de São Paulo São Carlos SP, Brazil 30 de Maio de 2014 Primeiro Semestre de 2014 Turma 2014106
Aplicações da Integral - Continuação e Técnicas de Integração Aula 33 Alexandre Nolasco de Carvalho Universidade de São Paulo São Carlos SP, Brazil 30 de Maio de 2014 Primeiro Semestre de 2014 Turma 2014106
8.1 Áreas Planas. 8.2 Comprimento de Curvas
 8.1 Áreas Planas Suponha que uma certa região D do plano xy seja delimitada pelo eixo x, pelas retas x = a e x = b e pelo grá co de uma função contínua e não negativa y = f (x) ; a x b, como mostra a gura
8.1 Áreas Planas Suponha que uma certa região D do plano xy seja delimitada pelo eixo x, pelas retas x = a e x = b e pelo grá co de uma função contínua e não negativa y = f (x) ; a x b, como mostra a gura
Universidade Federal da Bahia
 Universidade Federal da Bahia Instituto de Matemática DISCIPLINA: MATA0 - CÁLCULO B UNIDADE I - LISTA DE EXERCÍCIOS Atualizada 0. Áreas de figuras planas em coordenadas cartesianas [] Determine a área
Universidade Federal da Bahia Instituto de Matemática DISCIPLINA: MATA0 - CÁLCULO B UNIDADE I - LISTA DE EXERCÍCIOS Atualizada 0. Áreas de figuras planas em coordenadas cartesianas [] Determine a área
Universidade Federal da Bahia
 Universidade Federal da Bahia Instituto de Matemática DISCIPLINA: MATA0 - CÁLCULO B UNIDADE I - LISTA DE EXERCÍCIOS Atualizada 00. Áreas de figuras planas em coordenadas cartesianas [] Determine a área
Universidade Federal da Bahia Instituto de Matemática DISCIPLINA: MATA0 - CÁLCULO B UNIDADE I - LISTA DE EXERCÍCIOS Atualizada 00. Áreas de figuras planas em coordenadas cartesianas [] Determine a área
Lista de Exercícios 1 Forças e Campos Elétricos
 Lista de Exercícios 1 Forças e Campos Elétricos Exercícios Sugeridos (21/03/2007) A numeração corresponde ao Livros Textos A e B. A19.1 (a) Calcule o número de elétrons em um pequeno alfinete de prata
Lista de Exercícios 1 Forças e Campos Elétricos Exercícios Sugeridos (21/03/2007) A numeração corresponde ao Livros Textos A e B. A19.1 (a) Calcule o número de elétrons em um pequeno alfinete de prata
TM Estática II
 TM 332 - Estática II Emílio Eiji Kavamura, MSc Departamento de Engenaharia Mecânica UFPR TM-332, 2012 emilio.kavamura@ufpr.br (UFPR) Estática 2012 1 / 78 Roteiro da aula Centróides e Baricentros Formas
TM 332 - Estática II Emílio Eiji Kavamura, MSc Departamento de Engenaharia Mecânica UFPR TM-332, 2012 emilio.kavamura@ufpr.br (UFPR) Estática 2012 1 / 78 Roteiro da aula Centróides e Baricentros Formas
Integral de funções de uma variável
 Integrais Múltiplas Integral de funções de uma variável x = b a n a b f x dx = lim m m i=1 f(x i ) x Integral Dupla Seja f uma função de duas variáveis definida no retângulo fechado. R = a, b x c, d =
Integrais Múltiplas Integral de funções de uma variável x = b a n a b f x dx = lim m m i=1 f(x i ) x Integral Dupla Seja f uma função de duas variáveis definida no retângulo fechado. R = a, b x c, d =
FEP Física Geral e Experimental para Engenharia I
 FEP2195 - Física Geral e Experimental para Engenharia I Prova P1-10/04/2008 - Gabarito 1. A luz amarela de um sinal de transito em um cruzamento fica ligada durante 3 segundos. A largura do cruzamento
FEP2195 - Física Geral e Experimental para Engenharia I Prova P1-10/04/2008 - Gabarito 1. A luz amarela de um sinal de transito em um cruzamento fica ligada durante 3 segundos. A largura do cruzamento
Aproximações Lineares e Diferenciais. Aproximações Lineares e Diferenciais. 1.Aproximações Lineares 2.Exemplos 3.Diferenciais 4.
 UNIVERSIDADE DO ESTADO DE MATO GROSSO CAMPUS UNIVERSITÁRIO DE SINOP FACULDADE DE CIÊNCIAS EXATAS E TECNOLÓGICAS CURSO DE ENGENHARIA CIVIL DISCIPLINA: CÁLCULO DIFERENCIAL E INTEGRAL I Aproximações Lineares
UNIVERSIDADE DO ESTADO DE MATO GROSSO CAMPUS UNIVERSITÁRIO DE SINOP FACULDADE DE CIÊNCIAS EXATAS E TECNOLÓGICAS CURSO DE ENGENHARIA CIVIL DISCIPLINA: CÁLCULO DIFERENCIAL E INTEGRAL I Aproximações Lineares
Lista 7 Funções de Uma Variável
 Lista 7 Funções de Uma Variável Aplicações de Integração i) y = sec 2 (x) y = cos(x), x = π x = π Áreas 1 Determine a área da região em cinza: Ache a área da região delimitada pela parábola y = x 2 a reta
Lista 7 Funções de Uma Variável Aplicações de Integração i) y = sec 2 (x) y = cos(x), x = π x = π Áreas 1 Determine a área da região em cinza: Ache a área da região delimitada pela parábola y = x 2 a reta
Lista 7 Funções de Uma Variável
 Lista 7 Funções de Uma Variável Aplicações de Integração i) y = sec x) y = cosx), x = π x = π Áreas 1 Determine a área da região em cinza: Ache a área da região delimitada pela parábola y = x a reta tangente
Lista 7 Funções de Uma Variável Aplicações de Integração i) y = sec x) y = cosx), x = π x = π Áreas 1 Determine a área da região em cinza: Ache a área da região delimitada pela parábola y = x a reta tangente
FENÔMENOS DE TRANSPORTE
 Universidade Federal Fluminense Escola de Engenharia Disciplina: FENÔMENOS DE TRANSPORTE Aula 5 Hidrostática Prof.: Gabriel Nascimento (Depto. de Engenharia Agrícola e Meio Ambiente) Elson Nascimento (Depto.
Universidade Federal Fluminense Escola de Engenharia Disciplina: FENÔMENOS DE TRANSPORTE Aula 5 Hidrostática Prof.: Gabriel Nascimento (Depto. de Engenharia Agrícola e Meio Ambiente) Elson Nascimento (Depto.
x 2 + (x 2 5) 2, x 0, (1) 5 + y + y 2, y 5. (2) e é positiva em ( 2 3 , + ), logo x = 3
 Página 1 de 4 Instituto de Matemática - IM/UFRJ Cálculo Diferencial e Integral I - MAC 118 Gabarito segunda prova - Escola Politécnica / Escola de Química - 13/06/2017 Questão 1: (2 pontos) Determinar
Página 1 de 4 Instituto de Matemática - IM/UFRJ Cálculo Diferencial e Integral I - MAC 118 Gabarito segunda prova - Escola Politécnica / Escola de Química - 13/06/2017 Questão 1: (2 pontos) Determinar
Volume de um sólido de Revolução
 Algumas aplicações da engenharia em estática, considerando um corpo extenso, e com distribuição continua de massa, uniforme ou não é necessário determinar-se e momento de inércia, centroide tanto de placas
Algumas aplicações da engenharia em estática, considerando um corpo extenso, e com distribuição continua de massa, uniforme ou não é necessário determinar-se e momento de inércia, centroide tanto de placas
MOVIMENTO ROTACIONAL E MOMENTO DE INÉRCIA
 MOVIMENTO ROTACIONAL E MOMENTO DE INÉRCIA 1.0 Definições Posição angular: utiliza-se uma medida de ângulo a partir de uma direção de referência. É conveniente representar a posição da partícula com suas
MOVIMENTO ROTACIONAL E MOMENTO DE INÉRCIA 1.0 Definições Posição angular: utiliza-se uma medida de ângulo a partir de uma direção de referência. É conveniente representar a posição da partícula com suas
Integração Usando Tabelas e Sistemas Algébricos Computacionais
 UNIVERSIDADE DO ESTADO DE MATO GROSSO CAMPUS UNIVERSITÁRIO DE SINOP FACULDADE DE CIÊNCIAS EXATAS E TECNOLÓGICAS CURSO DE ENGENHARIA CIVIL DISCIPLINA: CÁLCULO DIFERENCIAL E INTEGRAL I Integração Usando
UNIVERSIDADE DO ESTADO DE MATO GROSSO CAMPUS UNIVERSITÁRIO DE SINOP FACULDADE DE CIÊNCIAS EXATAS E TECNOLÓGICAS CURSO DE ENGENHARIA CIVIL DISCIPLINA: CÁLCULO DIFERENCIAL E INTEGRAL I Integração Usando
APÊNDICE I Alguns procedimentos de obtenção do centro de gravidade de. figuras planas
 245 APÊNDICE I Alguns procedimentos de obtenção do centro de gravidade de figuras planas 1. Demonstração da localização do centro de gravidade de um paralelogramo por Arquimedes (287-212 a.c) Arquimedes
245 APÊNDICE I Alguns procedimentos de obtenção do centro de gravidade de figuras planas 1. Demonstração da localização do centro de gravidade de um paralelogramo por Arquimedes (287-212 a.c) Arquimedes
UNIVERSIDADE ESTADUAL DE SANTA CRUZ - UESC PRÓ-REITORIA DE GRADUAÇÃO - PROGRAD DEPARTAMENTO DE CIÊNCIAS EXATAS E TECNOLÓGICAS - DCET CÁLCULO IV
 UNIVESIDADE ESTADUAL DE SANTA CUZ - UESC PÓ-EITOIA DE GADUAÇÃO - POGAD DEPATAMENTO DE CIÊNCIAS EXATAS E TECNOLÓGICAS - DCET GUIA DE ESTUDO N 0 2 CÁLCULO IV OBJETIVOS: Proporcionar o ábito de leitura no
UNIVESIDADE ESTADUAL DE SANTA CUZ - UESC PÓ-EITOIA DE GADUAÇÃO - POGAD DEPATAMENTO DE CIÊNCIAS EXATAS E TECNOLÓGICAS - DCET GUIA DE ESTUDO N 0 2 CÁLCULO IV OBJETIVOS: Proporcionar o ábito de leitura no
MAT Aula 24/ Quarta 04/06/2014. Sylvain Bonnot (IME-USP)
 MAT 0143 Aula 24/ Quarta 04/06/2014 Sylvain Bonnot (IME-USP) 2014 1 Volumes Ideia: cortar o objeto em cilindros de base A(x) e altura dx, e depois fazer a soma b A(x)dx, onde A(x) é a área da secção transversal.
MAT 0143 Aula 24/ Quarta 04/06/2014 Sylvain Bonnot (IME-USP) 2014 1 Volumes Ideia: cortar o objeto em cilindros de base A(x) e altura dx, e depois fazer a soma b A(x)dx, onde A(x) é a área da secção transversal.
Aula 6. Doravante iremos dizer que r(t) é uma parametrização da curva, e t é o parâmetro usado para descrever a curva.
 Curvas ou Funções Vetoriais: Aula 6 Exemplo 1. Círculo como coleção de vetores. Vetor posição de curva: r(t) = (cos t, sen t), t 2π r(t) pode ser vista como uma função vetorial: r : [, 2π] R R 2 Doravante
Curvas ou Funções Vetoriais: Aula 6 Exemplo 1. Círculo como coleção de vetores. Vetor posição de curva: r(t) = (cos t, sen t), t 2π r(t) pode ser vista como uma função vetorial: r : [, 2π] R R 2 Doravante
25 de novembro de 2009
 MECÂNICA - 25 de novembro de 2009 Superfícies e volumes de revolução Teoremas de Pappus-Guldinus No século IV d.c., Pappus, um matemático grego de Alexandria, desenvolvou duas fórmulas que fornecem meios
MECÂNICA - 25 de novembro de 2009 Superfícies e volumes de revolução Teoremas de Pappus-Guldinus No século IV d.c., Pappus, um matemático grego de Alexandria, desenvolvou duas fórmulas que fornecem meios
GOVERNO FEDERAL MINISTÉRIO DA EDUCAÇÃO UNIVERSIDADE FEDERAL DO VALE DO SÃO FRANCISCO CÂMPUS JUAZEIRO/BA COLEG. DE ENG.
 GOVERNO FEDERAL MINISTÉRIO DA EDUCAÇÃO UNIVERSIDADE FEDERAL DO VALE DO SÃO FRANCISCO CÂMPUS JUAZEIRO/BA COLEG. DE ENG. ELÉTRICA PROF. PEDRO MACÁRIO DE MOURA CÁLCULO II 2015.2 Discente CPF Turma A2 Sala
GOVERNO FEDERAL MINISTÉRIO DA EDUCAÇÃO UNIVERSIDADE FEDERAL DO VALE DO SÃO FRANCISCO CÂMPUS JUAZEIRO/BA COLEG. DE ENG. ELÉTRICA PROF. PEDRO MACÁRIO DE MOURA CÁLCULO II 2015.2 Discente CPF Turma A2 Sala
Lista 12. Aula 39. Alexandre Nolasco de Carvalho Universidade de São Paulo São Carlos SP, Brazil
 Revisão - Resolução de Exerícios Aula 39 Alexandre Nolasco de Carvalho Universidade de São Paulo São Carlos SP, Brazil 13 de Junho de 2014 Primeiro Semestre de 2014 Turma 2014106 - Engenharia Mecânica
Revisão - Resolução de Exerícios Aula 39 Alexandre Nolasco de Carvalho Universidade de São Paulo São Carlos SP, Brazil 13 de Junho de 2014 Primeiro Semestre de 2014 Turma 2014106 - Engenharia Mecânica
Índice. AULA 6 Integrais trigonométricas 3. AULA 7 Substituição trigonométrica 6. AULA 8 Frações parciais 8. AULA 9 Área entre curvas 11
 www.matematicaemexercicios.com Integrais (volume ) Índice AULA 6 Integrais trigonométricas 3 AULA 7 Substituição trigonométrica 6 AULA 8 Frações parciais 8 AULA 9 Área entre curvas AULA Volumes 3 www.matematicaemexercicios.com
www.matematicaemexercicios.com Integrais (volume ) Índice AULA 6 Integrais trigonométricas 3 AULA 7 Substituição trigonométrica 6 AULA 8 Frações parciais 8 AULA 9 Área entre curvas AULA Volumes 3 www.matematicaemexercicios.com
A Regra da Cadeia. V(h) = 3h 9 h 2, h (0,3).
 Universidade de Brasília Departamento de Matemática Cálculo 1 A Regra da Cadeia Suponha que, a partir de uma lona de plástico com 6 metros de comprimento e 3 de largura, desejamos construir uma barraca
Universidade de Brasília Departamento de Matemática Cálculo 1 A Regra da Cadeia Suponha que, a partir de uma lona de plástico com 6 metros de comprimento e 3 de largura, desejamos construir uma barraca
Cálculo I - Lista 7: Integrais II
 Faculdade de Zootecnia e Engenharia de Alimentos Universidade de São Paulo - Prof. Responsável: Andrés Vercik. Use o teorema fundamental do calculo para achar a derivada da função. g( ) = + tdt g ( ) =
Faculdade de Zootecnia e Engenharia de Alimentos Universidade de São Paulo - Prof. Responsável: Andrés Vercik. Use o teorema fundamental do calculo para achar a derivada da função. g( ) = + tdt g ( ) =
Física Aplicada. Capítulo 03 Conceitos Básicos sobre Mecânica. Técnico em Edificações. Prof. Márcio T. de Castro 17/05/2017
 Física Aplicada Capítulo 03 Conceitos Básicos sobre Mecânica Técnico em Edificações 17/05/2017 Prof. Márcio T. de Castro Parte I 2 Mecânica Mecânica: ramo da física dedicado ao estudo do estado de repouso
Física Aplicada Capítulo 03 Conceitos Básicos sobre Mecânica Técnico em Edificações 17/05/2017 Prof. Márcio T. de Castro Parte I 2 Mecânica Mecânica: ramo da física dedicado ao estudo do estado de repouso
Momentos de Inércia de Superfícies
 PUC Goiás Curso: Engenharia Civil Disciplina: Mecânica dos Sólidos Corpo Docente: Geisa Pires Turma:----------- Plano de Aula Data: ------/--------/---------- Leitura obrigatória Mecânica Vetorial para
PUC Goiás Curso: Engenharia Civil Disciplina: Mecânica dos Sólidos Corpo Docente: Geisa Pires Turma:----------- Plano de Aula Data: ------/--------/---------- Leitura obrigatória Mecânica Vetorial para
MAT Cálculo Diferencial e Integral para Engenharia III 1a. Lista de Exercícios - 1o. semestre de x+y
 MAT455 - Cálculo Diferencial e Integral para Engenharia III a. Lista de Exercícios - o. semestre de. Calcule as seguintes integrais duplas: (a) R (y 3xy 3 )dxdy, onde R = {(x, y) : x, y 3}. Resp. (a) 585
MAT455 - Cálculo Diferencial e Integral para Engenharia III a. Lista de Exercícios - o. semestre de. Calcule as seguintes integrais duplas: (a) R (y 3xy 3 )dxdy, onde R = {(x, y) : x, y 3}. Resp. (a) 585
Universidade de Mogi das Cruzes UMC. Cálculo Diferencial e Integral II Parte IV
 Cálculo Diferencial e Integral II Página 1 Universidade de Mogi das Cruzes UMC Campos Villa Lobos Cálculo Diferencial e Integral II Parte IV Engenharia Civil Engenharia Mecânica marilia@umc.br º semestre
Cálculo Diferencial e Integral II Página 1 Universidade de Mogi das Cruzes UMC Campos Villa Lobos Cálculo Diferencial e Integral II Parte IV Engenharia Civil Engenharia Mecânica marilia@umc.br º semestre
(j) e x. 2) Represente geometricamente e interprete o resultado das seguintes integrais: (i) 1x dx Resposta: (ii)
 MINISTÉRIO DA EDUCAÇÃO DESEMPENHO UNIVERSIDADE TECNOLÓGICA FEDERAL DO PARANÁ CÂMPUS PATO BRANCO Atividades Práticas Supervisionadas (APS) de Cálculo Diferencial e Integral Prof a Dayse Batistus, Dr a.
MINISTÉRIO DA EDUCAÇÃO DESEMPENHO UNIVERSIDADE TECNOLÓGICA FEDERAL DO PARANÁ CÂMPUS PATO BRANCO Atividades Práticas Supervisionadas (APS) de Cálculo Diferencial e Integral Prof a Dayse Batistus, Dr a.
Cálculo II Segunda Aula: Aplicações das Integrais Definidas
 Cálculo II Segunda Aula: Aplicações das Integrais Definidas Prof. Jefferson Abrantes (Universidade Federal de Campina Grande) Unidade Acadêmica de Matemática-UAMat Campina Grande-PB Volumes por seções
Cálculo II Segunda Aula: Aplicações das Integrais Definidas Prof. Jefferson Abrantes (Universidade Federal de Campina Grande) Unidade Acadêmica de Matemática-UAMat Campina Grande-PB Volumes por seções
REVISAO GERAL. GRANDEZA ESCALAR É caracterizada por um número real. Como, por exemplo, o tempo, a massa, o volume, o comprimento, etc.
 MECÂNICA APLICADA 5º Período de Engenharia Civil REVISAO GERAL GRANDEZA ESCALAR É caracterizada por um número real. Como, por exemplo, o tempo, a massa, o volume, o comprimento, etc. GRANDEZA VETORIAL
MECÂNICA APLICADA 5º Período de Engenharia Civil REVISAO GERAL GRANDEZA ESCALAR É caracterizada por um número real. Como, por exemplo, o tempo, a massa, o volume, o comprimento, etc. GRANDEZA VETORIAL
2 de novembro de 2009
 MECÂNICA - de novembro de 009 6 massa e Centróide de um Aplicações; Conceitos e definições; Determinação da localização. Aplicações Para projetar a estrutura de apoio de um tanque de água, é necessário
MECÂNICA - de novembro de 009 6 massa e Centróide de um Aplicações; Conceitos e definições; Determinação da localização. Aplicações Para projetar a estrutura de apoio de um tanque de água, é necessário
CÁLCUL O INTEGRAIS TRIPLAS ENGENHARIA
 CÁLCUL O INTEGRAIS TRIPLAS ENGENHARIA 1 INTERPRETAÇÃO GEOMÉTRICA DE Nas integrais triplas, temos funções f(x,y,z) integradas em um volume dv= dx dy dz, sendo a região de integração um paralelepípedo P=
CÁLCUL O INTEGRAIS TRIPLAS ENGENHARIA 1 INTERPRETAÇÃO GEOMÉTRICA DE Nas integrais triplas, temos funções f(x,y,z) integradas em um volume dv= dx dy dz, sendo a região de integração um paralelepípedo P=
Gabarito - Primeira Verificação Escolar de Cálculo IIIA GMA Turma C1. x 2. 2 y
 Universidade Federal Fluminense Andrés Gabarito - Primeira Verificação Escolar de álculo IIIA GMA - Turma. onsidere a integral dupla a Esboce a região. y Temos que onde Observando que f(x, ydxdy + y {(x,
Universidade Federal Fluminense Andrés Gabarito - Primeira Verificação Escolar de álculo IIIA GMA - Turma. onsidere a integral dupla a Esboce a região. y Temos que onde Observando que f(x, ydxdy + y {(x,
Prof. MSc. David Roza José -
 1/22 2/22 Introdução Até o momento consideramos que a força de atração exercida pela terra num corpo rígido poderia ser representada por uma única força W, aplicada no centro de gravidade do corpo. O quê
1/22 2/22 Introdução Até o momento consideramos que a força de atração exercida pela terra num corpo rígido poderia ser representada por uma única força W, aplicada no centro de gravidade do corpo. O quê
Flexão Vamos lembrar os diagramas de força cortante e momento fletor
 Flexão Vamos lembrar os diagramas de força cortante e momento fletor Elementos longos e retos que suportam cargas perpendiculares a seu eixo longitudinal são denominados vigas. Vigas são classificadas
Flexão Vamos lembrar os diagramas de força cortante e momento fletor Elementos longos e retos que suportam cargas perpendiculares a seu eixo longitudinal são denominados vigas. Vigas são classificadas
Nunca desista dos seus sonhos!!!
 Nunca desista dos seus sonhos!!! LOQ 4083 - enômenos de Transporte I T I 05 orça Hidrostática em Superfícies Submersas Prof. Lucrécio ábio dos Santos Departamento de Engenharia Química LOQ/EEL tenção:
Nunca desista dos seus sonhos!!! LOQ 4083 - enômenos de Transporte I T I 05 orça Hidrostática em Superfícies Submersas Prof. Lucrécio ábio dos Santos Departamento de Engenharia Química LOQ/EEL tenção:
Qual é a posição do Centro de Massa de um corpo de material homogêneo que possui um eixo de simetria
 Valter B. Dantas Imagem e texto protegida por direitos autorais. Copia proibida. Geometria das Massas Centro de Massa de um Sistema Contínuo de Partículas Qual é a posição do Centro de Massa de um corpo
Valter B. Dantas Imagem e texto protegida por direitos autorais. Copia proibida. Geometria das Massas Centro de Massa de um Sistema Contínuo de Partículas Qual é a posição do Centro de Massa de um corpo
Capítulo 2 Pressão da água e forças de pressão
 Capítulo 2 Pressão da água e forças de pressão slide 1 Pressão absoluta e pressão manométrica Uma superfície de água em contato com a atmosfera terrestre está sujeita à pressão atmosférica. Na água em
Capítulo 2 Pressão da água e forças de pressão slide 1 Pressão absoluta e pressão manométrica Uma superfície de água em contato com a atmosfera terrestre está sujeita à pressão atmosférica. Na água em
. Use esta regra para calcular um valor aproximado de 1
 MAT 2 - a Lista de Exercícios. Faça o gráfico de F(t) = t f(x). Calcule F nos pontos onde a derivada existe, para as seguintes funções: (a) f(x) =, se x > e f(x) =, se x (b) f(x) = x, se x > e f(x) = 2,
MAT 2 - a Lista de Exercícios. Faça o gráfico de F(t) = t f(x). Calcule F nos pontos onde a derivada existe, para as seguintes funções: (a) f(x) =, se x > e f(x) =, se x (b) f(x) = x, se x > e f(x) = 2,
Funções Trigonométricas
 UNIVERSIDADE DO ESTADO DE MATO GROSSO CAMPUS UNIVERSITÁRIO DE SINOP FACULDADE DE CIÊNCIAS EXATAS E TECNOLÓGICAS CURSO DE ENGENHARIA CIVIL DISCIPLINA: CÁLCULO DIFERENCIAL E INTEGRAL I Funções Trigonométricas
UNIVERSIDADE DO ESTADO DE MATO GROSSO CAMPUS UNIVERSITÁRIO DE SINOP FACULDADE DE CIÊNCIAS EXATAS E TECNOLÓGICAS CURSO DE ENGENHARIA CIVIL DISCIPLINA: CÁLCULO DIFERENCIAL E INTEGRAL I Funções Trigonométricas
CÁLCUL O INTEGRAI S DUPLAS ENGENHARIA
 CÁLCUL O INTEGRAI S DUPLAS ENGENHARIA 1 INTERPRETAÇÃO GEOMÉTRICA DE Nas integrais simples, nós somamos os valores de uma função f(x) em comprimentos dx. Agora, nas integrais duplas fazemos o mesmo, mas
CÁLCUL O INTEGRAI S DUPLAS ENGENHARIA 1 INTERPRETAÇÃO GEOMÉTRICA DE Nas integrais simples, nós somamos os valores de uma função f(x) em comprimentos dx. Agora, nas integrais duplas fazemos o mesmo, mas
A integral definida Problema:
 A integral definida Seja y = f(x) uma função definida e limitada no intervalo [a, b], e tal que f(x) 0 p/ todo x [a, b]. Problema: Calcular (definir) a área, A,da região do plano limitada pela curva y
A integral definida Seja y = f(x) uma função definida e limitada no intervalo [a, b], e tal que f(x) 0 p/ todo x [a, b]. Problema: Calcular (definir) a área, A,da região do plano limitada pela curva y
CENTRO DE CIÊNCIAS E TECNOLOGIA AGROALIMENTAR UNIDADE ACADÊMICA DE TECNOLOGIA DE ALIMENTOS DISCIPLINA: FÍSICA II FLUIDOS. Prof.
 CENTRO DE CIÊNCIAS E TECNOLOGIA AGROALIMENTAR UNIDADE ACADÊMICA DE TECNOLOGIA DE ALIMENTOS DISCIPLINA: FÍSICA II FLUIDOS Prof. Bruno Farias Fluidos Os fluidos desempenham um papel vital em muitos aspectos
CENTRO DE CIÊNCIAS E TECNOLOGIA AGROALIMENTAR UNIDADE ACADÊMICA DE TECNOLOGIA DE ALIMENTOS DISCIPLINA: FÍSICA II FLUIDOS Prof. Bruno Farias Fluidos Os fluidos desempenham um papel vital em muitos aspectos
DIFERENCIAIS E O CÁLCULO APROXIMADO
 BÁRBARA DENICOL DO AMARAL RODRIGUEZ CINTHYA MARIA SCHNEIDER MENEGHETTI CRISTIANA ANDRADE POFFAL DIFERENCIAIS E O CÁLCULO APROXIMADO 1 a Edição Rio Grande 2017 Universidade Federal do Rio Grande - FURG
BÁRBARA DENICOL DO AMARAL RODRIGUEZ CINTHYA MARIA SCHNEIDER MENEGHETTI CRISTIANA ANDRADE POFFAL DIFERENCIAIS E O CÁLCULO APROXIMADO 1 a Edição Rio Grande 2017 Universidade Federal do Rio Grande - FURG
UNIVERSIDADE ESTADUAL DE SANTA CRUZ UESC. 1 a Avaliação escrita de Cálculo IV Professor: Afonso Henriques Data: 10/04/2008
 1 a Avaliação escrita de Professor: Afonso Henriques Data: 10/04/008 1. Seja R a região do plano delimitada pelos gráficos de y = x, y = 3x 18 e y = 0. Se f é continua em R, exprima f ( x, y) da em termos
1 a Avaliação escrita de Professor: Afonso Henriques Data: 10/04/008 1. Seja R a região do plano delimitada pelos gráficos de y = x, y = 3x 18 e y = 0. Se f é continua em R, exprima f ( x, y) da em termos
ALUNO(A): Nº TURMA: TURNO: DATA: / / COLÉGIO:
 Professor: Edney Melo ALUNO(A): Nº TURMA: TURNO: DATA: / / COLÉGIO: 1. Cálculo Diferencial Em vários ramos da ciência, é necessário algumas vezes utilizar as ferramentas básicas do cálculo, inventadas
Professor: Edney Melo ALUNO(A): Nº TURMA: TURNO: DATA: / / COLÉGIO: 1. Cálculo Diferencial Em vários ramos da ciência, é necessário algumas vezes utilizar as ferramentas básicas do cálculo, inventadas
Mecânica Geral. Prof. Evandro Bittencourt (Dr.) Engenharia de Produção e Sistemas UDESC. 27 de fevereiro de 2008
 Mecânica Geral Prof Evandro Bittencourt (Dr) Engenharia de Produção e Sistemas UDESC 7 de fevereiro de 008 Sumário 1 Prof Evandro Bittencourt - Mecânica Geral - 007 1 Introdução 11 Princípios Fundamentais
Mecânica Geral Prof Evandro Bittencourt (Dr) Engenharia de Produção e Sistemas UDESC 7 de fevereiro de 008 Sumário 1 Prof Evandro Bittencourt - Mecânica Geral - 007 1 Introdução 11 Princípios Fundamentais
Universidade Tecnológica Federal do Paraná. APS Cálculo 2
 Ministério da Educação Universidade Tecnológica Federal do Paraná Campus Campo Mourão Wellington José Corrêa Nome: APS Cálculo 2 1. As dimensões de uma caixa retangular fechada foram medidas com 80 cm,
Ministério da Educação Universidade Tecnológica Federal do Paraná Campus Campo Mourão Wellington José Corrêa Nome: APS Cálculo 2 1. As dimensões de uma caixa retangular fechada foram medidas com 80 cm,
1. A partir da definição, determinar a equação da parábola P, cujo foco é F = (3, 4) e cuja diretriz é L : x + y 2 = 0. (x 3) 2 + (y + 4) 2 =
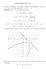 QUESTÕES-AULA 18 1. A partir da definição, determinar a equação da parábola P, cujo foco é F = (3, 4) e cuja diretriz é L : x + y = 0. Solução Seja P = (x, y) R. Temos que P P d(p, F ) = d(p, L) (x 3)
QUESTÕES-AULA 18 1. A partir da definição, determinar a equação da parábola P, cujo foco é F = (3, 4) e cuja diretriz é L : x + y = 0. Solução Seja P = (x, y) R. Temos que P P d(p, F ) = d(p, L) (x 3)
A Derivada. Derivadas Aula 16. Alexandre Nolasco de Carvalho Universidade de São Paulo São Carlos SP, Brazil
 Derivadas Aula 16 Alexandre Nolasco de Carvalho Universidade de São Paulo São Carlos SP, Brazil 04 de Abril de 2014 Primeiro Semestre de 2014 Turma 2014104 - Engenharia Mecânica A Derivada Seja x = f(t)
Derivadas Aula 16 Alexandre Nolasco de Carvalho Universidade de São Paulo São Carlos SP, Brazil 04 de Abril de 2014 Primeiro Semestre de 2014 Turma 2014104 - Engenharia Mecânica A Derivada Seja x = f(t)
Curso de Férias de IFVV (Etapa 3) INTEGRAIS DUPLAS
 Curso de Férias de IFVV (Etapa ) INTEGAIS UPLAS VOLUMES E INTEGAIS UPLAS Objetivando resolver o problema de determinar áreas, chegamos à definição de integral definida. A idéia é aplicar procedimento semelhante
Curso de Férias de IFVV (Etapa ) INTEGAIS UPLAS VOLUMES E INTEGAIS UPLAS Objetivando resolver o problema de determinar áreas, chegamos à definição de integral definida. A idéia é aplicar procedimento semelhante
MAT Cálculo Diferencial e Integral para Engenharia III 1a. Lista de Exercícios - 1o. semestre de 2013
 MAT55 - Cálculo iferencial e Integral para Engenharia III a. Lista de Exercícios - o. semestre de. Calcule as seguintes integrais duplas: (a) (y xy )dxdy, onde = {(x, y) : x, y }. esp. (a) 585 8. (b) x
MAT55 - Cálculo iferencial e Integral para Engenharia III a. Lista de Exercícios - o. semestre de. Calcule as seguintes integrais duplas: (a) (y xy )dxdy, onde = {(x, y) : x, y }. esp. (a) 585 8. (b) x
3 a Ficha de Exercícios de AMIII
 3 a Ficha de Exercícios de MIII Resolução Sumária. Escreva fdv como um integral iterado nas duas ordens de integração possíveis, onde o conjunto é: O triângulo de vértices,,, e, ; região entre os gráficos
3 a Ficha de Exercícios de MIII Resolução Sumária. Escreva fdv como um integral iterado nas duas ordens de integração possíveis, onde o conjunto é: O triângulo de vértices,,, e, ; região entre os gráficos
ENG1200 Mecânica Geral Semestre Lista de Exercícios 6 Corpos Submersos
 ENG1200 Mecânica Geral Semestre 2013.2 Lista de Exercícios 6 Corpos Submersos 1 Prova P3 2013.1 - O corpo submerso da figura abaixo tem 1m de comprimento perpendicularmente ao plano do papel e é formado
ENG1200 Mecânica Geral Semestre 2013.2 Lista de Exercícios 6 Corpos Submersos 1 Prova P3 2013.1 - O corpo submerso da figura abaixo tem 1m de comprimento perpendicularmente ao plano do papel e é formado
Algumas Regras para Diferenciação
 UNIVERSIDADE DO ESTADO DE MATO GROSSO CAMPUS UNIVERSITÁRIO DE SINOP FACULDADE DE CIÊNCIAS EXATAS E TECNOLÓGICAS CURSO DE ENGENHARIA CIVIL DISCIPLINA: CÁLCULO DIFERENCIAL E INTEGRAL I Algumas Regras para
UNIVERSIDADE DO ESTADO DE MATO GROSSO CAMPUS UNIVERSITÁRIO DE SINOP FACULDADE DE CIÊNCIAS EXATAS E TECNOLÓGICAS CURSO DE ENGENHARIA CIVIL DISCIPLINA: CÁLCULO DIFERENCIAL E INTEGRAL I Algumas Regras para
MAT Cálculo Diferencial e Integral para Engenharia III 1a. Lista de Exercícios - 1o. semestre de 2016
 MAT55 - Cálculo iferencial e Integral para ngenharia III a. Lista de xercícios - o. semestre de 6. Calcule as seguintes integrais duplas: (a) (y xy )dxdy, onde = {(x, y) : x, y }. esp. (a) 585. 8 x sin
MAT55 - Cálculo iferencial e Integral para ngenharia III a. Lista de xercícios - o. semestre de 6. Calcule as seguintes integrais duplas: (a) (y xy )dxdy, onde = {(x, y) : x, y }. esp. (a) 585. 8 x sin
UNIFEI - UNIVERSIDADE FEDERAL DE ITAJUBÁ
 UNIFEI - UNIVERSIDADE FEDERAL DE ITAJUBÁ PROVA DE CÁLCULO e 2 PROVA DE TRANSFERÊNCIA INTERNA, EXTERNA E PARA PORTADOR DE DIPLOMA DE CURSO SUPERIOR - 6//26 CANDIDATO: CURSO PRETENDIDO: OBSERVAÇÕES:. Prova
UNIFEI - UNIVERSIDADE FEDERAL DE ITAJUBÁ PROVA DE CÁLCULO e 2 PROVA DE TRANSFERÊNCIA INTERNA, EXTERNA E PARA PORTADOR DE DIPLOMA DE CURSO SUPERIOR - 6//26 CANDIDATO: CURSO PRETENDIDO: OBSERVAÇÕES:. Prova
INTEGRAIS MÚLTIPLAS. [a, b] e [c, d], respectivamente. O conjunto P = {(x i, y j ) i = 0,..., n, j = i=1
![INTEGRAIS MÚLTIPLAS. [a, b] e [c, d], respectivamente. O conjunto P = {(x i, y j ) i = 0,..., n, j = i=1 INTEGRAIS MÚLTIPLAS. [a, b] e [c, d], respectivamente. O conjunto P = {(x i, y j ) i = 0,..., n, j = i=1](/thumbs/99/142468356.jpg) Teoria INTEGRAIS MÚLTIPLAS Integral Dupla: Seja o retângulo R = {(x, y) R a x b, c y d} e a = x 0 < x 1
Teoria INTEGRAIS MÚLTIPLAS Integral Dupla: Seja o retângulo R = {(x, y) R a x b, c y d} e a = x 0 < x 1
Capítulo 5 Integral. Definição Uma função será chamada de antiderivada ou de primitiva de uma função num intervalo I se: ( )= ( ), para todo I.
 Capítulo 5 Integral 1. Integral Indefinida Em estudos anteriores resolvemos o problema: Dada uma função, determinar a função derivada. Desejamos agora estudar o problema inverso: Dada uma função, determinar
Capítulo 5 Integral 1. Integral Indefinida Em estudos anteriores resolvemos o problema: Dada uma função, determinar a função derivada. Desejamos agora estudar o problema inverso: Dada uma função, determinar
Integral definida. Prof Luis Carlos Fabricação 2º sem
 Integral definida Prof Luis Carlos Fabricação 2º sem Cálculo de Áreas Para calcular esta área, aproximamos a região por retângulos e fazemos o número de retângulos se tornar muito grande. A área exata
Integral definida Prof Luis Carlos Fabricação 2º sem Cálculo de Áreas Para calcular esta área, aproximamos a região por retângulos e fazemos o número de retângulos se tornar muito grande. A área exata
Integrais Duplos e Triplos.
 Capítulo 4 Integrais uplos e Triplos. 4.1 Integrais uplos xercício 4.1.1 Calcule os seguintes integrais. a. e. 1 1 e 1 2x+2 15xy + 1y 2 dy dx b. y x dx dy 4 x 2y) dy dx f. 4 1 π 6 2 π 2 x 1 6xy 3 + x )
Capítulo 4 Integrais uplos e Triplos. 4.1 Integrais uplos xercício 4.1.1 Calcule os seguintes integrais. a. e. 1 1 e 1 2x+2 15xy + 1y 2 dy dx b. y x dx dy 4 x 2y) dy dx f. 4 1 π 6 2 π 2 x 1 6xy 3 + x )
11 Aplicações da Integral
 Aplicações da Itegral Ao itroduzirmos a Itegral Defiida vimos que ela pode ser usada para calcular áreas sob curvas. Veremos este capítulo que existem outras aplicações. Essas aplicações estedem-se aos
Aplicações da Itegral Ao itroduzirmos a Itegral Defiida vimos que ela pode ser usada para calcular áreas sob curvas. Veremos este capítulo que existem outras aplicações. Essas aplicações estedem-se aos
1 - NOÇÕES DE HIDRÁULICA - Cont
 UNIVERSIDDE FEDERL DE GOIÁS ESCOL DE GRONOMI E ENGENHRI DE LIMENTOS SETOR DE ENGENHRI RURL Prof. dão Wagner Pêgo Evangelista 1 - NOÇÕES DE HIDRÁULIC - Cont 1.2 HIDROSTÁTIC 1.2.1 Conceitos de pressão e
UNIVERSIDDE FEDERL DE GOIÁS ESCOL DE GRONOMI E ENGENHRI DE LIMENTOS SETOR DE ENGENHRI RURL Prof. dão Wagner Pêgo Evangelista 1 - NOÇÕES DE HIDRÁULIC - Cont 1.2 HIDROSTÁTIC 1.2.1 Conceitos de pressão e
Exercícios de Cálculo - Prof. Ademir
 Exercícios de Cálculo - Prof. Ademir Funções, limites e continuidade. Considere f : IR IR definida por f(x) = x 4x + 3. (a) Faça um esboço do gráfico de f. (b) Determine os valores de x para os quais f(x)..
Exercícios de Cálculo - Prof. Ademir Funções, limites e continuidade. Considere f : IR IR definida por f(x) = x 4x + 3. (a) Faça um esboço do gráfico de f. (b) Determine os valores de x para os quais f(x)..
2 Integrais Duplas em Coordenadas Polares
 Lista 3: CDCI2 Turmas: 2AEMN e 2BEMN Prof. Alexandre Alves Universidade São Judas Tadeu 1 Mudança de Variáveis em Integrais Duplas Exercício 1: Calcule a integral dupla transformando a região de integração
Lista 3: CDCI2 Turmas: 2AEMN e 2BEMN Prof. Alexandre Alves Universidade São Judas Tadeu 1 Mudança de Variáveis em Integrais Duplas Exercício 1: Calcule a integral dupla transformando a região de integração
CÁLCULO I. 1 Taxa de Variação. Objetivos da Aula. Aula n o 15: Taxa de Variação. Taxas Relacionadas. Denir taxa de variação;
 CÁLCULO I Prof. Marcos Diniz Prof. Edilson Neri Prof. André Almeida Aula n o 15: Taxa de Variação. Taxas Relacionadas Objetivos da Aula Denir taxa de variação; Usar as regras de derivação no cálculo de
CÁLCULO I Prof. Marcos Diniz Prof. Edilson Neri Prof. André Almeida Aula n o 15: Taxa de Variação. Taxas Relacionadas Objetivos da Aula Denir taxa de variação; Usar as regras de derivação no cálculo de
CÁLCULO I. Lista Semanal 01 - Gabarito
 CÁLCULO I Prof. Márcio Nascimento Prof. Marcos Diniz Questão 1. Nos itens abaixo, diga se o problema pode ser resolvido com seus conhecimentos de ensino médio (vamos chamar de pré-cálculo) ou se são necessários
CÁLCULO I Prof. Márcio Nascimento Prof. Marcos Diniz Questão 1. Nos itens abaixo, diga se o problema pode ser resolvido com seus conhecimentos de ensino médio (vamos chamar de pré-cálculo) ou se são necessários
Derivadas Parciais Capítulo 14
 Derivadas Parciais Capítulo 14 DERIVADAS PARCIAIS Como vimos no Capítulo 4, no Volume I, um dos principais usos da derivada ordinária é na determinação dos valores máximo e mínimo. DERIVADAS PARCIAIS 14.7
Derivadas Parciais Capítulo 14 DERIVADAS PARCIAIS Como vimos no Capítulo 4, no Volume I, um dos principais usos da derivada ordinária é na determinação dos valores máximo e mínimo. DERIVADAS PARCIAIS 14.7
Aplicações de integração. Cálculo 2 Prof. Aline Paliga
 Aplicações de integração Cálculo Prof. Aline Paliga Áreas entre curvas Nós já definimos e calculamos áreas de regiões que estão sob os gráficos de funções. Aqui nós estamos usando integrais para encontrar
Aplicações de integração Cálculo Prof. Aline Paliga Áreas entre curvas Nós já definimos e calculamos áreas de regiões que estão sob os gráficos de funções. Aqui nós estamos usando integrais para encontrar
FEP Física Geral e Experimental para Engenharia I
 FEP195 - Física Geral e Experimental para Engenharia I Prova P3 - Gabarito 1. Três partículas de massa m estão presas em uma haste fina e rígida de massa desprezível e comprimento l. O conjunto assim formado
FEP195 - Física Geral e Experimental para Engenharia I Prova P3 - Gabarito 1. Três partículas de massa m estão presas em uma haste fina e rígida de massa desprezível e comprimento l. O conjunto assim formado
Apresentação do Cálculo
 UNIVERSIDADE DO ESTADO DE MATO GROSSO CAMPUS UNIVERSITÁRIO DE SINOP FACULDADE DE CIÊNCIAS EXATAS E TECNOLÓGICAS CURSO DE ENGENHARIA CIVIL DISCIPLINA: CÁLCULO DIFERENCIAL E INTEGRAL I Apresentação do Cálculo
UNIVERSIDADE DO ESTADO DE MATO GROSSO CAMPUS UNIVERSITÁRIO DE SINOP FACULDADE DE CIÊNCIAS EXATAS E TECNOLÓGICAS CURSO DE ENGENHARIA CIVIL DISCIPLINA: CÁLCULO DIFERENCIAL E INTEGRAL I Apresentação do Cálculo
Solução: Alternativa (c). Esse movimento é retilíneo e uniforme. Portanto h = (g t 1 2 )/2 e 2 h =
 UNIVERSIDADE FEDERAL DE ITAJUBÁ FÍSICA PROVA DE TRANSFERÊNCIA INTERNA, EXTERNA E PARA PORTADOR DE DIPLOMA DE CURSO SUPERIOR 9/06/206 CANDIDATO: CURSO PRETENDIDO: OBSERVAÇÕES: 0 Prova sem consulta. 02 Duração:
UNIVERSIDADE FEDERAL DE ITAJUBÁ FÍSICA PROVA DE TRANSFERÊNCIA INTERNA, EXTERNA E PARA PORTADOR DE DIPLOMA DE CURSO SUPERIOR 9/06/206 CANDIDATO: CURSO PRETENDIDO: OBSERVAÇÕES: 0 Prova sem consulta. 02 Duração:
