Legenda. Questões. 2ª Lista de Exercícios (ALI0001) Prof. Helder G. G. de Lima 1. Cálculos Conceitos Teoria
|
|
|
- Camila Godoi Botelho
- 5 Há anos
- Visualizações:
Transcrição
1 2ª Lista de Exercícios (ALI0001) Prof. Helder G. G. de Lima 1 Legenda Cálculos Conceitos Teoria Questões 1. Revise todos os axiomas da definição de espaço vetorial V sobre o corpo de escalares R, verificando a validade de cada um deles nos seguintes conjuntos. Em cada item, as operações de adição e multiplicação por escalar que aparecem no lado esquerdo são as do espaço vetorial que está sendo definido, e as do lado direito são operações usuais de R. (a) V = R n, formado por todas as sequências de n números reais, e (x 1,..., x n ) + (y 1,..., y n ) = (x 1 + y 1,..., x n + y n ) k (x 1,..., x n ) = (kx 1,..., kx n ) (b) V = M m n (R), formado por todas as matrizes de ordem m n, com m, n fixos e (A + B) ij = (A) ij + (B) ij, para 1 i m e 1 j n, (k B) ij = k(a ij ), para 1 i m e 1 j n (c) V = F(R) = F(, + ), formado por todas as funções f : R R e (f + g)(x) = f(x) + g(x), x R (k f)(x) = k(f(x)), x R (d) V = C, formado por todos os números complexos e (a + bi) + (c + di) = (a + c) + (b + d)i k (a + bi) = (ka) + (kb)i (e) V = R, formado por todas as sequências infinitas de números reais, e (x 1, x 2,...) + (y 1, y 2,...) = (x 1 + y 1, x 2 + y 2,...) k (x 1,..., x n ) = (kx 1, kx 2,...) 2. Verifique se as operações definidas a seguir fazem com que os conjuntos V indicados sejam espaços vetoriais. Em particular, determine se há algum elemento z V que faz o papel de vetor nulo, ou seja, que satisfaz z + v = v, v V, e para cada vetor v V, indique qual x V é o seu oposto, no sentido de que x + v = z. 1 Este é um material de acesso livre distribuído sob os termos da licença Creative Commons Atribuição- CompartilhaIgual 4.0 Internacional
2 { x + y = x + y + 1, x V, y V (a) V = R, sendo k x = kx + k 1, k R, x V { (b) V = R 2 (x, y) + (u, v) = (x + u, y + v), (x, y) V, (u, v) V, sendo k (x, y) = ( 3kx + ky, 5kx 2ky), k R, (x, y) V { (c) V = R 2 (x, y) + (u, v) = (x + u + 1, y + v 2), (x, y) V, (u, v) V, sendo k (x, y) = (kx + k 1, ky 2k + 2), k R, (x, y) V 3. Seja V = R 4, o espaço vetorial das quádruplas de números reais, com as operações usuais. Mostre que os seguintes subconjuntos são subespaços vetoriais de V : (a) U = {(a, b, c, d) R 4 a b = c + d}. (b) W = {(a, b, c, d) R 4 c = d = 0}. 4. Seja V = M 3 3 (R), o espaço vetorial das matrizes quadradas de ordem 3, com as operações usuais. Mostre que os seguintes subconjuntos são subespaços vetoriais de V : (a) As matrizes simétricas: S = {X M 3 3 (R) X T = X}. (b) As matrizes antissimétricas: A = {X M 3 3 (R) X T = X}. (c) As matrizes que comutam com uma matriz B fixada: C = {X V BX = XB}. (d) U = {A = (a ij ) M 3 3 (R) a ij = 0 sempre que i + j 4}. 5. Seja V = F(R). Mostre que os seguintes subconjuntos são subespaços vetoriais de V : (a) O conjunto P formado por todas as funções polinomiais (de qualquer grau): P = {p(x) F(R) p(x) = a n x n +...+a 1 x 1 +a 0, para algum natural n, e a i R}. (b) Dado um natural n, o conjunto P n de todos polinômios de grau menor ou igual a n: P n = {q(x) P grau(q(x)) n}. (c) As funções pares, isto é, tais que f( x) = f(x), para todo x R. (d) As funções ímpares, isto é, tais que f( x) = f(x), para todo x R. (e) O conjunto C 0 (R) das funções contínuas (f) O conjunto C 1 (R) das funções deriváveis cuja derivada é contínua 6. Em cada item, determine se U é ou não um subespaço do espaço vetorial V indicado: (a) V = R 2 e U = {(x, y) R 2 y + 2x = 5} (b) V = R 2 e U = {(x, y) R 2 y = 4x} (c) V = M 3 1 (R), U = {X M 3 1 (R) AX = 0}, sendo A = [ ] (d) V = M 2 2 (R) e U = {Z M 2 2 (R) Z tem zeros em sua diagonal} (e) V = M 2 2 (R) e U = {B M 2 2 (R) det(b) 0} (f) V = F(R) e U = {f F(R) f é um polinômio de grau exatamente igual a 3} (g) V = F(R) e U = {f F(R) f ( 1) = f (1) = 0} 2
3 7. Sejam A = [ ] , B = [ ] e C = Resolva a seguinte equação na variável X M 3 2 (R): [ ] vetores de M (R). A X X + B = C Prove que os únicos subespaços de R (com as operações usuais) são o trivial {0} e R. (dica: mostre que se U é um subespaço de R e U {0} então U = R) 9. Seja U um subespaço de um espaço vetorial V. Explique por que W = {x V x U} não pode ser um subespaço de V. 10. Para cada um dos subespaços vetoriais U e V a seguir, obtenha o subespaço U V : (a) U = {ax 3 +bx 2 +cx+d P 3 (R) 3a b+c+d = 0} e V = {p(x) P 3 (R) p ( 1) = 0} (b) U = {g F(R) g é par} e V = {g F(R) g é ímpar} (c) U = {M M n n (R) M é antissimétrica} e V = {M M n n (R) M é simétrica} 11. Seja V um espaço vetorial qualquer e U um subespaço de V. Prove que para quaisquer vetores x, y V vale o seguinte: se x U e y x U então y U. 12. Dê exemplos de subespaços vetoriais V 1 e V 2 de R 3 que satisfaçam as seguintes condições (e explique porque satisfazem): (a) V 1 V 2 não é subespaço vetorial de R 3 (b) V 1 V 2 é subespaço vetorial de R Sejam V 1 e V 2 quaisquer subespaços de um espaço vetorial W arbitrário. Prove que para V 1 V 2 ser subespaço vetorial de W é preciso que V 1 V 2 ou que V 2 V Explique todas as afirmações verdadeiras a seguir, e dê contra-exemplos para as demais. (a) A interseção de dois subespaços vetoriais de V nunca é vazia. (b) Se V = ger {u 1, u 2, u 3 } então {u 1, u 2, u 3 } é uma base de V (c) Se {u, v} é linearmente dependente (L.D.) então um dos vetores é múltiplo do outro. (d) Se u 0 então os vetores u e u são linearmente independentes (L.I.). (e) Se {u, v} é L.I. e {v, w} é L.I. então {u, v, w} é L.I.. (f) Se {u} é L.I. e {v} é L.I. então {u, v} é L.I.. (g) É possível que u ger {v, w} sem que ocorra u ger {v} nem u ger {w}. 15. É verdade que R 4 = ger {(1, 1, 0, 0), (0, 0, 1, 1), (0, 2, 1, 0), (0, 0, 1, 1)}? Por que? 16. Encontre um conjunto de vetores geradores de um dos seguintes subespaços de M 3 3 (R): (a) D = {X M 3 3 (R) X é diagonal } (b) W = {A M 3 3 (R) A é antissimétrica } (c) U = {B M 3 3 (R) B é simétrica } 17. Verifique se os conjuntos {v 1,..., v n } a seguir são formados por vetores linearmente independentes (L. I.) ou linearmente dependentes (L. D.): (a) v 1 = (0, 3, 9), v 2 = (1, 4, 10), v 3 = (2, 5, 11) em R 3. 3
4 (b) v 1 = (0, 3, 9), v 2 = (1, 4, 10) em R 3. [ ] [ ] [ ] (c) v 1 =, v =, v =, v = [ ] 0 1, v = [ ] 1 2 em M (R). (d) v 1 = x 3 + x 2 + x + 1, v 2 = x 2 + x + 1, v 3 = x + 1, v 4 = 1 no espaço de polinômios P Encontre uma base e a dimensão de cada um dos seguintes espaços vetoriais: (a) V = R 4 = {(x, y, z, w) x R, y R, z R, w R}. { [ ] } a b c (b) V = M 2 3 (R) = a R, b R, c R, p R, q R, r R. p q r (c) V = P 5 = {p(x) F(R) p(x) é um polinômio de grau 5}. 19. Encontre uma base e a dimensão do subespaço W de V nos seguintes casos: (a) V = R 3 e W = {(x, y, z) z = 0} (o plano horizontal que passa pela origem). (b) V = M 2 2 (R) e W = {S V S T = S} (as matrizes simétricas 2 2) (c) V = F(R) e W = {p(x) = ax 2 + bx + c P 2 p (6) = 0} (geometricamente, estas funções correspondem a parábolas com vértice em (6, f(6))). (d) V = R 4 e W = {(x, y, z, w) x + 2w = 0, y = 2w, w = z/2}. 20. Encontre um subconjunto de S = {(1, 1, 1), (1, 1, 0), (1, 0, 1), (0, 1, 1)} que seja base de R Mostre que {0, v 1,..., v n } é um conjunto de vetores linearmente dependente, isto é, todo conjunto de vetores contendo o vetor nulo é linearmente dependente. 22. Prove que se W = ger {v 1,..., v n } e z W então W = ger {v 1,..., v n, z}. 23. Prove que se S 1 = {u 1, u 2, u 3 } é um conjunto de vetores linearmente independentes, então S 2 = {u 1, u 2 } também é um conjunto de vetores linearmente independentes. 24. Dada uma matriz A, denote por L(A) o espaço linha (subespaço gerado pelas linhas de A), por C(A) o espaço coluna (subespaço gerado pelas colunas de A) e por N(A) o núcleo de A (o espaço das matrizes coluna X que satisfazem AX = 0). Encontre uma base e a dimensão de L(A), C(A) e N(A) para as seguintes matrizes: [ ] [ ] (a) A = (b) A = [ ] (c) A = [ (d) A = Se U e V são subespaços de um espaço vetorial W, denota-se o conjunto de todas as somas de elementos de U com elementos de V por U +V = {x+y W x U e y V }. Esta soma é chamada de soma direta, e denotada por U V, se ocorrer U V = {0}. Encontre U + V para os seguintes subespaços U e V e verifique se é uma soma direta: (a) Em W = R 4, os subespaços U = {(x, y, z, w) R 4 V = {(a, b, c, d) R 4 b = 2c}. ] T x + y = 0 = z + w} e (b) Os subespaços U = {M M 3 3 (R) M T = M} das matrizes antissimétricas e V = {N M 3 3 (R) N T = N} das matrizes simétricas de W = M 3 3 (R). 4
5 (c) Os subespaços U = {q(x) = b 0 + b 1 x + b 2 x 2 + b 3 x 3 q( x) = q(x), x R} e V = {p(x) = a 0 + a 1 x + a 2 x 2 + a 3 x 3 p( x) = p(x), x R} do espaço vetorial P Encontre uma base e a dimensão de cada uma das somas U + V do exercício anterior. 27. Mostre que se u, v e w são vetores L. I. então os vetores u + v, u v e u w são L. I. 28. Mostre que se B = {u, v} é uma base de V então V = ger {u} ger {v}. 29. Sejam U = ger {(1, 0, 0), (2, 1, 1)} e V = ger {(0, 1, 0), (0, 0, 1)} subespaços de R 3. (a) Encontre uma base e a dimensão de U V. (b) Verifique se R 3 = U + V e se R 3 = U V. 30. Mostre que se B = {u, v} é uma base de V então B = {u + v, u v} também é base. 5
6 Respostas 1. Todos os axiomas de espaço vetorial devem ser checados individualmente. A comutatividade da adição, por exemplo, seria verificada como segue: (a) (x 1,..., x n ) + (y 1,..., y n ) = (x 1 + y 1,..., x n + y n ) = (y 1 + x 1,..., y n + x n ) = (y 1,..., y n ) + (x 1,..., x n ). O vetor nulo é a sequência com as n coordenadas iguais a zero: 0 = (0,..., 0). (b) (A + B) ij = (A) ij + (B) ij = (B) ij + (A) ij = (B + A) ij. O vetor nulo é a matriz nula 0 = 0 m n em que 0 ij = 0, i, j. (c) (f + g)(x) = f(x) + g(x) = g(x) + f(x) = (g + f)(x), x R. O vetor nulo é a função constante igual a zero: f(x) = 0, x R. (d) (a + bi) + (c + di) = (a + c) + (b + d)i = (c + a) + (d + b)i = (c + di) + (a + bi). O vetor nulo é o número complexo (e, de fato, real) 0 = 0 + 0i. (e) (x 1, x 2,...) + (y 1, y 2,...) = (x 1 + y 1, x 2 + y 2,...) = (y 1 + x 1, y 2 + x 2,...) = (y 1, y 2,...) + (x 1, x 2,...). O vetor nulo é a sequência infinita com todas as posições iguais a zero: 0 = (0, 0,...). 2. (a) R é um espaço vetorial com as operações indicadas. O vetor nulo é 1 e x 2 é o oposto do vetor x. (b) R 2 não é espaço vetorial com as operações indicadas, pois 1 (x, y) = ( 3x + y, 5x 2y) (x, y), para vários valores de x, y. (c) R 2 é um espaço vetorial com as operações indicadas. O vetor nulo é ( 1, 2) e o vetor oposto de (x, y) é ( x 2, y + 4). 3. (a) Se u = (a, b, c, d) U e v = (p, q, r, s) U, então a b = c + d e p q = r + s. Assim, como u + v = (a + p, b + q, c + r, d + s) tem-se (a + p) (b + q) = (a b) + (p q) = (c + d) + (r + s) = (c + r) + (d + s), ou seja, u + v R. Do mesmo modo, se k R, tem-se ku = (ka, kb, kc, kd) e ka kb = k(a b) = k(c + d) = kc + kd, ou seja, ku R. Note ainda que o vetor 0 = (0, 0, 0, 0) U. (b) W = {(a, b, c, d) R 4 c = d = 0}. Dados (a, b, 0, 0) W e (c, d, 0, 0) W, tem-se (a, b, 0, 0) + (c, d, 0, 0) = (a + c, b + d, 0 + 0, 0 + 0) = (a + c, b + d, 0, 0) W e k(a, b, 0, 0) = (ka, kb, k0, k0) = (ka, kb, 0, 0) W 4. (a) Se X e Y são matrizes simétricas então X T = X e Y T = Y. Consequentemente, (X + Y ) T = X T + Y T = X + Y, ou seja, X + Y é simétrica. Dado k R, (kx) T = k(x T ) = kx, ou seja, kx é simétrica. Note que a matriz nula também é simétrica. (b) Se X e Y são matrizes antissimétricas então X T = X e Y T = Y. Consequentemente, (X + Y ) T = X T + Y T = X + ( Y ) = (X + Y ), ou seja, X + Y é antissimétrica. Dado k R, (kx) T = k(x T ) = k( X) = (kx), ou seja, kx é antissimétrica. Note que a matriz nula também é antissimétrica. 6
7 (c) Se X e Y comutam com B, então BX = XB e BY = Y B. Consequentemente, B(X + Y ) = BX + BY = XB + Y B = (X + Y )B, ou seja, X + Y comuta com B. Dado k R, B(kX) = k(bx) = k(xb) = (kx)b, ou seja, kx comuta com B. Note que B0 = 0B = 0, isto é, a matriz nula também comuta com B. (d) U = {A = (a ij ) M 3 3 (R) a ij = 0 sempre que i + j 4}. A condição que define 0 0 a 13 o conjunto U indica que para toda matriz A U é da forma A = 0 a 22 0, a pois a 11 = a 12 = a 21 = a 23 = a 32 = a 33 = 0 (em particular, a matriz nula 3 3 está em U). Além disso, ao somar A U com B U, as entradas [A + B] ij em que i + j 4 serão iguais a zero pois [A + B] ij = a ij + b ij = = 0. Logo, A + B U, e este é um conjunto fechado para a adição. multiplicação por um escalar k R, tem-se: Em relação à [ka] ij = ka ij = k0 = 0, ou seja, ka U (a multiplicação por escalar é fechada em U), e conclui-se que U é um subespaço de M 3 3 (R). 5. (a) Se p e q são polinômios e c R, a soma p+q e o produto c p também são polinômios, logo p + q P e cp P. Mais precisamente, se p(x) = a n x n a 1 x 1 + a 0 e q(x) = b m x m b 1 x 1 + b 0, com m, n N e a i, b i R então p + q é dado por (p + q)(x) = p(x) + q(x) = (a n x n a 1 x 1 + a 0 ) + (b m x m b 1 x 1 + b 0 ) = (a k + b k )x k (a 1 + b 1 )x 1 + (a 0 + b 0 ) P, onde k é o maior dos graus m e n. De forma análoga, (c p)(x) = c p(x) = c(a n x n a 1 x 1 + a 0 ) = (ca n )x n (ca 1 )x 1 + (ca 0 ) P. Perceba que o polinômio nulo (p(x) = 0) é o vetor nulo neste espaço vetorial. (b) Dado um natural n, o conjunto P n de todos polinômios de grau menor ou igual a n: P n = {p(x) P grau(p(x)) n}. Pelo exercício anterior, a soma de polinômios resulta em um polinômio, e a multiplicação de um polinômio por um escalar real qualquer também é um polinômio. Levando isso em conta, para ver que P n é um subespaço vetorial de F(R) basta lembrar que se p, q P n então: ˆ grau(p + q) < grau(p) + grau(q), se os termos de maior grau são opostos ˆ grau(p + q) = grau(p) + grau(q), nos demais casos ˆ grau(c p) = grau(p) se c 0; ˆ grau(c p) = grau(0) < grau(p), se c = 0 Este último item também mostra que o polinômio nulo é um elemento de P n. 7
8 (c) Se f e g são funções pares, então para todo x R tem-se (f + g)( x) = f( x) + g( x) = f(x) + g(x) = (f + g)(x), ou seja, f + g também é par. Analogamente, dado qualquer c R, (cf)( x) = cf( x) = cf(x) = (cf)(x), e portanto cf também é par, e o conjunto dado é um subespaço de F(R). A função constante igual a zero, que é o vetor nulo deste espaço, é uma função par. (d) Se f e g são funções ímpares, então para todo x R tem-se (f +g)( x) = f( x)+g( x) = ( f(x))+( g(x)) = (f(x)+g(x)) = (f +g)(x), ou seja, f + g também é ímpar. Analogamente, dado qualquer c R, (cf)( x) = cf( x) = c( f(x)) = c(f(x)) = (cf)(x), e portanto cf também é ímpar e o conjunto é fechado para ambas as operações do espaço vetorial, ou seja, é um subespaço de F(R). A função constante igual a zero também é uma função ímpar. (e) Como a soma de funções contínuas é contínua e a multiplicação de funções contínuas por constantes resulta em funções contínuas, conclui-se que C 0 (R) é fechado para ambas as operações do espaço vetorial, e consequentemente é um subespaço de F(R). (f) Sejam f, g C 1 (R) e c R. Então: ˆ As funções f e g são deriváveis e suas derivadas são contínuas. Como a soma de funções deriváveis é uma função derivável, f + g também é derivável e vale (f + g) = f + g. Além disso, pelo exercício anterior f + g é contínua, pois é soma de funções contínuas. Logo, f + g é uma função derivável cuja derivada é contínua, ou seja, f + g C 1 (R). ˆ Sendo f derivável, a função cf também é derivável e (cf) = c(f ). Mas f é contínua, então c(f ) também é (pelo exercício anterior), ou seja, cf C 1 (R). Como as duas operações são fechadas, segue que C (R) é um subespaço de F(R). 6. (a) Como (0, 0) é o vetor nulo de R 2 e (0, 0) U, pois , este conjunto U não é um subespaço vetorial de R 2 (geometricamente, é uma reta que não passa pela origem). Note que a adição e a multiplicação por escalar não são fechadas em U. Por exemplo, (0, 5) + (3, 1) = (3, 4) U pois ( 1) 5. (b) Sejam (a, b) U, (c, d) U e k R. Então ˆ (a, b) + (c, d) = (a + c, b + d) U pois b + d = ( 4a) + ( 4c) = 4(a + c). ˆ k(a, b) = (ka, kb) U pois kb = k( 4a) = 4(ka). Portanto, U é um subespaço vetorial de R 2 (é a reta que passa pela origem e tem a direção do vetor (1, 4)) (c) U = {X M 3 1 (R) AX = 0} é um subespaço vetorial de V = M 3 1 (R) pois ˆ A0 = 0, ou seja, a matriz nula 3 1 pertence a U. ˆ Se AX 1 = 0 e AX 2 = 0 então A(X 1 + X 2 ) = AX 1 + AX 2 = ˆ Se AX = 0 e t R então A(tX) = t(ax) = t0 = 0. 8
9 Em outras palavras, U é fechado para as operações do espaço vetorial V. Note que as propriedades acima são válidas independentemente de quais sejam os números que aparecem na matriz A, então não é necessário expandir os produtos em termos das entradas das matrizes. De fato, U = N(A), isto é, é o espaço nulo de A. { [ ] } 0 z12 (d) Note que U = z z , z 21 R e que para todo X, Y U e m R tem-se: [ ] [ ] [ ] 0 x12 0 y12 0 x ˆ X + Y = + = 12 + y 12 U x 21 0 [ ] 0 x12 ˆ mx = m = x 21 0 y 21 0 [ 0 mx12 mx 21 0 Portanto, U é um subespaço vetorial de V. x 21 + y 21 0 ] U (e) O conjunto U consiste das matrizes 2 2 que são inversíveis. Como I e I são matrizes inversíveis (det(i) = det( I) = 1 0), e sua soma I + ( I) = 0 não é inversível (pois det(0) = 0), conclui-se que U não é fechado para a adição, e como tal não é um subespaço de V. A multiplicação por escalar também não é fechada em U, pois a ao multiplicar uma matriz inversível por zero o resultado é a matriz nula, que não pertence a U. (f) Os polinômios de grau 3 não formam um espalo vetorial pois, por exemplo, se p(x) = 4x 3 + 5x e q(x) = 4x 3 então p(x) + q(x) = 5x que não tem grau 3. (g) Sejam f, g U. Então f ( 1) = f (1) = 0 e g ( 1) = g (1) = 0. Consequentemente: ˆ (f + g) (1) = f (1) + g (1) = = 0 ˆ (f + g) ( 1) = f ( 1) + g ( 1) = = 0 Isto significa que a adição é fechada em U. De forma análoga, para todo c R vale: ˆ (cf) (1) = c(f (1)) = c 0 = 0 ˆ (cf) ( 1) = c(f ( 1)) = c 0 = 0 Isto significa que a multiplicação por escalar também é fechada, e assim U é um subespaço vetorial de F(R). 7. Sabendo que A, B e X são elementos do espaço vetorial M 3 2, pode-se utilizar as propriedades deste espaço (associatividade, comutatividade, etc) para isolar a incógnita X, de forma análoga ao que seria feito se A, B e X fossem números reais: A X 5 X + B 2 Assim, X = 1 7 ( 2 ( A X = C 10 5 X + B 2 ) = 10C 2(A X) 5(X + B) = 10C 2A 2X 5X 5B = 10C 7X = 2A + 10C + 5B X = 1 (2A 10C 5B) 7 [ ] [ ] [ ] ) = [ 6 5 ] Se U é um subespaço de R e U {0} então U tem algum elemento não nulo. Denote-o por b. Para ver que todo número real x também tem que estar em U basta escrever x = ( x b ) b, pois sendo U um subespaço vetorial de R ele é fechado para a multiplicação por escalar e portanto a multiplicação de b U pelo escalar x deve resultar em um elemento de U, b isto é, x U. Portanto U = R. 9. O conjunto W = {x V x U} não é um subespaço de V pois 0 U mas 0 W. 9
10 10. (a) Primeiramente lembre-se que se p(x) = ax 3 +bx 2 +cx+d então p (x) = 3ax 2 +2bx+c e p ( 1) = 3a 2b + c. Assim, U V = {ax 3 + bx 2 + cx + d P 3 (R) 3a b + c + d = 0 e 3a 2b + c = 0}. Em outras palavras, os coeficientes de p(x) são soluções do sistema linear homogêneo { 3a b + c + d = 0 3a 2b + c = 0 Escalonando a matriz associada ao sistema, obtem-se: [ ] [ ] [ ] 3 L 1 1 1/3 1/3 1/3 L 2 3L 1 1 1/3 1/3 1/ [ ] [ ] L 2 1 1/3 1/3 1/3 L L /3 2/ ou seja, a = 1 ( c 2d) e b = d, em que c, d R são variáveis livres. Assim, 3 { U V = ax 3 + bx 2 + cx + d P 3 (R) a = { ( c 2d = 3 c 2d 3 ) x 3 + ( d)x 2 + cx + d c, d R } e b = d, sendo c, d R } (b) Se g U então para todo x R ocorre g( x) = g(x) e se, além disso, g V então para todo x R vale g( x) = g(x). Neste caso, para todo x R tem-se g(x) = g( x) = g(x), ou seja 2g(x) = 0 e portanto g(x) = 0. Assim, a única função que está simultaneamente em U e em V é a função constante igual a zero, que é o vetor nulo de F(R), isto é, U V = {0}. (c) Se M U então M T = M e se, além disso, M V então M T = M. Neste caso, tem-se M = M T = M, ou seja 2M = 0 e portanto M = 0. Assim, a única matriz que é simétrica e antissimétrica é a matriz nula, ou seja, U V = {0}. 11. Para quaisquer x, y V tem-se y = (y x) + x. Então se x U e y x U e U é um subespaço de V, então U é fechado para a adição, e consequentemente y = (y x)+x U. 12. Dê exemplos de subespaços vetoriais V 1 e V 2 de R 3 que satisfaçam as seguintes condições (e explique porque satisfazem): (a) Sejam ˆ V 1 = {(x, y, z) R 3 z = 0} ˆ V 2 = {(x, y, z) R 3 x = 0} Então o conjunto V 1 V 2 = {(x, y, z) R 3 z = 0 ou x = 0} não é um subespaço de R 3 pois (1, 1, 0) V 1 V 2 e (0, 1, 1) V 1 V 2 mas (1, 1, 0)+(0, 1, 1) = (1, 2, 1) V 1 V 2. (b) Sejam ˆ V 1 = R 3 ˆ V 2 = {(0, 0, 0)} Então V 1 V 2 = R 3 {(0, 0, 0)} = R 3, que é, naturalmente, um subespaço de R
11 13. Suponha que V 1 e V 2 são subespaços de W tais que V 1 V 2 também é subespaço de W. Se V 1 não estiver contido em V 2, é porque existe algum vetor x 1 V 1 que não pertence a V 2, e pode-se deduzir que V 2 V 1 da seguinte forma: dado um vetor x 2 V 2 arbitrário, tanto x 1 quanto x 2 são elementos de V 1 V 2. Assumindo que esta união seja um subespaço, a soma x 1 + x 2 deve pertencer a V 1 V 2. Ou seja, x 1 + x 2 deve ser elemento de V 1 ou de V 2 : (a) Para que x 1 +x 2 fosse elemento de V 2 seria preciso que x 1 = (x 1 +x 2 ) x 2 V 2 (pois V 2 é subespaço). Mas foi assumido que x 1 V 2, então só resta a outra possibilidade; (b) Sendo x 1 + x 2 um elemento de V 1, resulta que x 2 = (x 1 + x 2 ) x 1 V 1. Em outras palavras, todo elemento x 2 de V 2 tem que pertencer a V 1, isto é, V 2 V (a) Verdadeira. Como todo subespaço vetorial deve conter o vetor nulo, a interseção de dois subespaços vetoriais quaisquer tem pelo menos um elemento, ou seja, não é vazia. (b) Falsa. Mesmo que V seja o espaço gerado por u 1, u 2, u 3, pode ser que um destes vetores seja combinação linear dos demais. Neste caso, os vetores são linearmente dependentes, e não são uma base de V. Por exemplo: R 2 = ger {(1, 0), (0, 1), (2, 3)}, mas (1, 1) = 2(1, 0) + 3(0, 1), ou seja, estes três vetores geram R 2 mas não são uma base. (c) Verdadeira. Se {u, v} é linearmente dependente, então existem a, b R tais que au + bv = 0, sem que ambos os coeficientes precisem ser nulos. Se, por exemplo, a 0, então pode-se escrever u = ( b a )v. E se b 0, então v = ( a )u. Em ambos b os casos, um dos vetores pode ser visto como um múltiplo do outro. (d) Falso. Os vetores u e u nunca são linearmente independentes, pois um deles é múltiplo do outro, e pode-se escrever au + b( u) = 0 com os escalares não nulos a = 1 e b = 1. (e) Falso. Mesmo que {u, v} sejam L.I. e que {v, w} seja L.I., pode acontecer de {u, v, w} ser L.D.. Por exemplo, em R 2, se u = (1, 0), v = (0, 1) e w = (1, 1) então w = u + v, ou seja, há uma combinação linear 1u + 1v + ( 1)w que resulta no vetor nulo sem que todos os coeficientes sejam nulos. (f) Falsa. Apesar de, separadamente, os vetores serem L.I., pode ocorrer que o conjunto contendo ambos seja L.D. Por exemplo, em R 3, o conjunto {(1, 0, 0)} é linearmente independente, e o conjunto {(5, 0, 0)} também. No entanto, como (5, 0, 0) = 5(1, 0, 0), o conjunto {(1, 0, 0), (5, 0, 0)} é linearmente dependente. (g) Verdadeira. Em R 2, considerando-se u = (2, 3), v = (1, 0) e w = (0, 1), observa-se que u = 2(1, 0) + 3(0, 1) = 2u + 3v ger {v, w}, mas u ger {v} e u ger {w}. 15. Para que R 4 = ger {u, v, x, z}, com u = (1, 1, 0, 0), v = (0, 0, 1, 1), x = (0, 2, 1, 0) e z = (0, 0, 1, 1) é necessário e suficiente que qualquer (a, b, c, d) possa ser escrito como uma combinação linear dos vetores u, v, x, z, isto é, que dado (a, b, c, d) R 4 exista alguma solução para a equação (a, b, c, d) = t 1 (1, 1, 0, 0) + t 2 (0, 0, 1, 1) + t 3 (0, 2, 1, 0) + t 4 (0, 0, 1, 1), que é equivalente a um sistema linear nas variáveis t 1, t 2, t 3 e t 4 : t 1 = a t 1 + 2t 3 = b t 2 t 2 + t 3 + t 4 = c + t 4 = d 11
12 ou ainda, à equação matricial t 1 t 2 t 3 t 4 a = b c. d Note que esta matriz poderia ser construída diretamente a partir dos vetores, copiando-se as coordenadas de u, v, x e z para as colunas da matriz. Como a matriz é quadrada, o sistema terá solução se, e somente se, ela for inversível, o que será verdade se o determinante da matriz for diferente de zero. Calculando-o pela primeira linha, obtém-se: = = = 2(1 1 ( 1) 1) = 4 0. Então, de fato, qualquer (a, b, c, d) é combinação linear dos quatro vetores dados, isto é, R 4 = ger {u, v, x, z}. 16. (a) Para toda matriz diagonal X M 3 3 (R) tem-se a X = 0 b 0 = a b c 0 0 0, 0 0 c c com a, b, c R. Então estas três matrizes geram D. (b) Para toda matriz antissimétrica A M 3 3 (R) tem-se 0 a b A = a 0 c = a b c 0 0 1, b c com a, b, c R. Então estas três matrizes geram W. (c) Para toda matriz simétrica B M 3 3 (R) tem-se a b c B = b d e = a b c d c e f e f 0 0 0, com a, b, c, d, e, f R. Então estas 6 matrizes geram U. 17. (a) v 1 = (0, 3, 9), v 2 = (1, 4, 10), v 3 = (2, 5, 11) em R 3. Suponha que c 1, c 2 e c 3 sejam escalares tais que c 1 v 1 + c 2 v 2 + c 3 v 3 = 0, isto é, que c 1 (0, 3, 9) + c 2 (1, 4, 10) + c 3 (2, 5, 11) = (0, 0, 0) ou ainda, (c 2 + 2c 3, 3c 1 + 4c 2 + 5c 3, 9c 1 10c 2 11c 3 ) = (0, 0, 0) 12
13 c 2 + 2c 3 = 0 Então c 1, c 2, c 3 são soluções do sistema linear homogêneo 3c 1 + 4c 2 + 5c 3 = 0 9c 1 10c 2 11c 3 = 0 Como o número de equações é o mesmo do número de incógnitas, pode-se determinar se c 1 = c 2 = c 3 = 0 é ou não a única solução calculando o determinante da matriz associada ao sistema: = ( 1) = ( 1) = 0 Como o determinante é zero, existem infinitas soluções não triviais e os vetores dados são linearmente dependentes. (b) v 1 = (0, 3, 9), v 2 = (1, 4, 10) em R 3. Pelo exercício 1, se v 1 e v 2 fossem linearmente dependentes, um deles seria múltiplo do outro. Mas estes dois vetores não são múltiplos, logo, só podem ser linearmente independentes. (c) A condição c 1 v 1 + c 2 v 2 + c 3 v 3 + c 4 v 4 + c 5 v 5 = 0 equivale às seguintes condições: [ ] [ ] [ ] [ ] [ ] [ ] c 1 c c c c = c 2 + c 3 + c 5 = 0 c c 1 + c 4 + 2c 5 = c 1 + 3c 5 = c 2 c 3 c 4c 2 + 4c 5 = = c 5 0 Escalonando a matriz deste sistema (ou encontrando as suas soluções por qualquer outro método) obtém-se: /2 1 L 3 2L 1 L 4 L 2 L 2 L 3 L L / / L 1 L L L / / L L L 3 L 4 c 1 = c 5 /2 c 2 = c 5 c 3 = 0 c 4 = c 5 Como o sistema tem c 5 como uma variável livre, é possível obter o vetor nulo como combinação linear das matrizes v 1,..., v 5 sem que todos os coeficientes sejam nulos (exemplo: 1v 1 2v 2 + 0v 3 + 5v 4 + 5v 5 = 0). Isto significa que estes vetores são linearmente dependentes. 13
14 (d) A condição av 1 + bv 2 + cv 3 + dv 4 = 0 equivale às seguintes condições: a(x 3 + x 2 + x + 1) + b(x 2 + x + 1) + c(x + 1) + d = 0x 3 + 0x 2 + 0x + 0 ax 3 + (a + b)x 2 + (a + b + c)x + (a + b + c + d) = 0x 3 + 0x 2 + 0x + 0 a = 0 a = 0 a + b = 0 b = 0 a + b + c = 0 c = 0 a + b + c + d = 0 d = 0 Como a única forma de obter o vetor nulo como combinação linear dos polinômios dados é usar todos os coeficientes iguais a zero, resulta que eles são linearmente independentes. 18. (a) Pode-se verificar que B = {(1, 0, 0, 0), (0, 1, 0, 0), (0, 0, 1, 0), (0, 0, 0, 1)} é uma base de R 4 e disto resulta que dim(r 4 ) = 4. { [ ] [ ] [ ] [ ] [ ] [ ] } (b) B =,,,,, é uma base de M 2 3 (R) (por que?) e consequentemente dim(m 2 3 (R)) = 6. (c) B = {1, x, x 2, x 3, x 4, x 5 } é uma base de P 5 (verifique!) e portanto dim(p 5 ) = (a) Tem-se u W se e somente se u = (x, y, 0), para algm x, y, R. Neste caso, u = x(1, 0, 0) + y(0, 1, 0). Portanto os vetores v 1 = (1, 0, 0) e v 2 = (0, 1, 0) geram W. Mas estes vetores são linearmente independentes, pois se k 1 v 1 + k 2 v 2 = 0 então k 1 (1, 0, 0) + k 2 (1, 0, 0) = (k 1, k 1, 0) = (0, 0, 0) o que significa que k 1 = k 2 = 0. Em outras palavras, o vetor nulo só pode ser obtido como combinação linear de v 1 e v 2 se todos os coeficientes forem nulos. Portanto, B = {(1, 0, 0), (0, 1, 0)} é uma base de W, e conclui-se que dim(w ) = 2. (b) Um vetor u V pertence a W se, e somente se [ ] [ ] [ ] [ ] a b u = = a + b + c, = av b c bv 2 + cv 3 [ ] [ ] [ ] em que v 1 =, v = e v = e a, b, c R. Isto significa que 0 1 W = ger {v 1, v 2, v 3 }. Além disso, se m 1 v 1 + m 2 v 2 + m 3 v 3 = 0, tem-se [ ] [ ] [ ] [ ] [ ] m1 m m 1 + m m = =, 0 1 m 2 m isto é, cada m i = 0, o que significa que os vetores v 1, v 2, v 3 são L.I. e B = {v 1, v 2, v 3 } é uma base de W. Consequentemente, dim(w ) = 3. (c) V = F(R) e W = {p(x) = ax 2 + bx + c P 2 p (6) = 0} (geometricamente, estas funções correspondem a parábolas com vértice em (6, f(6))). Dado p(x) = ax 2 +bx+c P 2 tem-se p (x) = 2ax+b. Então p(x) W se, e somente se 2a(6) + b = 0, ou seja, b = 12a. Assim, todo elemento de W é da forma p(x) = ax 2 + ( 12a)x + c = a (x 2 12x) + c 1, com a, c R. Em outras palavras, os polinômios q 1 = x 2 12x e q 2 = 1 geram W. Estes vetores também são linearmente independentes pois 14
15 c 1 = 0 c 1 (x 2 12x) + c 2 (1) = 0 c 1 x 2 12c 1 x + c 2 = 0 12c 1 = 0 c 2 = 0 Portanto, B = ger {1, x 2 12x} é uma base de W e dim(w ) = 2. (d) Como x + 2w = 0 x = 2w y = 2w y = 2w w = z/2 z = 2w { c 1 = 0 c 2 = 0 resulta que u W se, e somente se, u = ( 2w, 2w, 2w, w) = w( 2, 2, 2, 1), com w R. Em outras palavras, W = ger {( 2, 2, 2, 1)}. Como este vetor é diferente de zero, B = {( 2, 2, 2, 1)} é L.I. pois 2k = 0 2k = 0 k( 2, 2, 2, 1) = (0, 0, 0, 0) 2k = 0 k = 0 Portanto B é uma base para W e dim(w ) = 1. k = Como (1, 1, 1) = 1 ((1, 1, 0) + (1, 0, 1) + (0, 1, 1)), pode-se dizer que S é L.D. (pois um dos 2 vetores é combinação linear dos demais, ou porque o sistema linear associado tem soluções não nulas) e portanto não forma uma base de R 3. No entanto, se forem considerados apenas os vetores v 1 = (1, 1, 0), v 2 = (1, 0, 1) e v 3 = (0, 1, 1), então o subconjunto B = {v 1, v 2, v 3 } será uma base de R 3 pois R 3 = ger {v 1, v 2, v 3 } e estes três vetores são L.I. De fato, qualquer (a, b, c) R 3 pode ser escrito como combinação linear de v 1, v 2 e v 3 pois x + y = a x = 1 (a + b c) 2 (a, b, c) = x(1, 1, 0) + y(1, 0, 1) + z(0, 1, 1) x + z = b y = 1 (a b + c) 2 y + z = c z = 1 ( a + b + c) 2 Além disso, com base no cálculo acima, o único modo de obter (a, b, c) = (0, 0, 0) como combinação linear de v 1, v 2 e v 3 é considerando todos os coeficientes x = y = z = Para que um conjunto de vetores seja L.D. deve ser possível expressar o vetor nulo como combinação linear deles sem que todos os coeficientes desta combinação linear sejam zero. No caso dos vetores 0, v 1,..., v n, pode-se usar, por exemplo, os escalares c 0 = 7, c 1 = 0, c 2 = 0,..., c n = 0 pois v v n = 0. Como pelo menos o escalar c 0 0, conclui-se que os vetores são linearmente dependentes. 22. Sejam W = ger {v 1,..., v n } e z W, isto é, z = k 1 v k n v n, com k 1,..., k n R. Sendo U = ger {v 1,..., v n, z}, pode-se dizer que os conjuntos U e W são iguais se for explicado por que todo elemento de W pertence a U e vice-versa (W U e U W ). ˆ Se u W, então u é uma combinação linear dos vetores v i, isto é, u = c 1 v c n v n. Mas então é claro que u também é combinação linear dos vetores v i e de z pois basta considerar um coeficiente zero para z, como em u = c 1 v c n v n + 0 z. Isto quer dizer que z ger {v 1,..., v n, z} = U, ou seja, que W U. 15
16 ˆ Por outro lado, todo u W é combinação linear de v 1,..., v n, z, isto é, u = d 1 v d n v n + d n+1 z = d 1 v d n v n + d n+1 (k 1 v k n v n ) = (d 1 + d n+1 k 1 )v (d n + d n+1 k n )v n. Portanto u é uma combinação linear dos vetores v 1,..., v n, o que quer dizer que u ger {v 1,..., v n } = W, ou seja, que U W. Em resumo, ao adicionar a uma lista de vetores v i um vetor z que já esteja no espaço gerado por eles, o espaço gerado por todos estes vetores continuará sendo o mesmo. 23. Suponha que au 1 + bu 2 = 0. Então au 1 + bu 2 + 0u 3 = 0, ou seja, tem-se uma combinação de u 1, u 2, u 3 que resulta no vetor nulo. Mas por hipótese, u 1, u 2, u 3 são L.I., então esta combinação linear precisa ter todos os coeficientes iguais a zero, isto é, a = b = 0. Assim, mostrou-se que não há outra forma de obter o vetor nulo como combinação linear de u 1 e u 2, isto é, u 1 e u 2 são L.I. 24. (a) i. Como o espaço linha da matriz A e o espaço linha de sua forma escalonada reduzida são os mesmos, pode-se utilizar as linhas não nulas da forma reduzida como vetores geradores de L(A). Para a matriz dada, o escalonamento consistirá destes passos: [ ] [ ] 1 1 L 2 L [ ] [ ] 2 L L 1 +L Então L(A) = ger { [ 1 0 ], [ 0 1 ] } = { [ a b ] a, b, R} = M 1 2 (R). Além disso, é claro que estes dois vetores linha são L.I. pois a [ 1 0 ] +b [ 0 1 ] = [ a b ] [ só pode ser igual a 0 0 ] se a e b forem ambos nulos. Em outras palavras, estes dois vetores formam uma base de L(A), que portanto é um espaço vetorial de dimensão dois. ii. Para o espaço coluna de A, pode-se usar como geradores as colunas de A que correspondem { [ às] posições [ ] } dos pivôs da forma reduzida. Especificamente, tem-se 1 1 C(A) = ger,. Estes dois vetores coluna são L.I. pois nenhum deles 1 1 é múltiplo do outro. Então eles formam uma base de C(A) e dim(c(a)) = 2. [ ] [ ] [ ] [ ] x 1 1 x 0 iii. O núcleo N(A) consiste dos vetores tais que =, isto é, as y { 1 1 y 0 x y = 0 coordenadas x, y são soluções do sistema linear x + y = 0. { [ ] } 0 Isto implica que x = y = 0 e que N(A) =. Portanto, o conjunto vazio 0 é uma base de N(A). Perceba que não faria sentido que a base tivesse algum vetor não nulo, pois senão ela geraria um espaço maior do que o espaço nulo; e também não faz sentido considerar apenas o vetor nulo como uma base, já que ele não seria L.I.. Logo a dimensão de N(A) é zero (não há vetores na base). (b) Note que A = [ ] está na forma escalonada reduzida por linhas, então: i. L(A) = ger { [ ] } e como este conjunto é L.I., dim(l(a)) = 1 ii. C(A) = ger { [ 1 ] } e como o conjunto é L.I. dim(c(a)) = 1 16
17 25. (...) 26. (...) 2y 3z 4w iii. N(A) = y z y, z, w R = ger 1 0, 0 1, 0 0 e w como os três vetores são L.I., dim(l(a)) = 3 [ ] (c) A matriz A = está na forma escalonada reduzida então: i. L(A) = ger { [ ], [ ] } e dim(l(a)) = 2 (os vetores são L.I.) { [ ] [ ] } 1 0 ii. C(A) = ger, e dim(c(a)) = z 1 0 iii. N(A) = w z y, z, w R = ger 0 1, 1 0 e dim(l(a)) = 2. w (d) A forma escalonada reduzida de A = é , então i. L(A) = ger { [ 1 2 ] } e dim(l(a)) = ii. C(A) = ger 0 e dim(c(a)) = { [ ] } { [ ] } 2y 2 iii. N(A) = y R = ger e dim(l(a)) = 1. y Suponha que a(u+v)+b(u v)+c(u w) = 0. Então (a+b+c)u+(a b)v +( c)w = 0 e como u, v, w são L.I. esta combinação linear só resulta no vetor nulo se os três coeficientes forem zero, isto é, se a + b + c = 0 a b = 0 c = 0 Mas a única solução deste sistema é a = b = c = 0, o que implica que vetores u + v, u v e u w são L.I Se B = {u, v} é uma base de V então V = ger {u} ger {v}, pois: ˆ V = ger {u}+ger {v}. De fato, como B é base, seus elementos geram V, ou seja todo w V pode ser escrito na forma w = αu + βv, com α, β R. Mas αu ger {u} e βv ger {v}, então w ger {u} + ger {v}, o que significa que V ger {u} + ger {v}. Reciprocamente, dado w ger {u} + ger {v}, tem-se w V, pois a soma de subespaços de V também é um subespaço de V. Assim, ger {u} + ger {v} V. 17
18 29. (...) ˆ ger {u} ger {v} = {0}. De fato, se w ger {u} ger {v} então w = αu e w = βv, para algum α, β R. Consequentemente, αu βv = 0 e o fato de u e v serem linearmente independentes implica que α = 0 e β = 0, ou seja, w = 0u = 0w = 0. Assim, ger {u} ger {v} {0}. Por outro lado, é imediato que {0} ger {u} ger {v}, pois a interseção de subespaços é um subespaço vetorial, e como tal deve conter o vetor nulo. 30. Se B = {u, v} é uma base de V, então dim V = 2 e qualquer conjunto linearmente independente com dois vetores gera (e é base de) V. Em particular, isso pode ser usado para mostrar que B é base: supondo que α 1 (u + v) + α 2 (u v) = 0, então (α 1 + α 2 )u + (α 1 α 2 )v = 0. Como u e v são linearmente independentes, então { α1 + α 2 = 0 α 1 α 2 = 0 o que implica que α 1 = α 2 = 0, pois este é um sistema homogêneo possível e determinado. Logo, B é linearmente independente e, portanto, uma base de V. 18
de adição e multiplicação por escalar definidas por: 2. Mostre que o conjunto dos polinômios da forma a + bx com as operações definidas por:
 Lista de Exercícios - Espaços Vetoriais. Seja V o conjunto de todos os pares ordenados de números reais e considere as operações de adição e multiplicação por escalar definidas por: i. u + v (x y) + (s
Lista de Exercícios - Espaços Vetoriais. Seja V o conjunto de todos os pares ordenados de números reais e considere as operações de adição e multiplicação por escalar definidas por: i. u + v (x y) + (s
1 a Lista de Exercícios MAT 3211 Álgebra Linear Prof. Vyacheslav Futorny
 1 a Lista de Exercícios MAT 3211 Álgebra Linear - 213 - Prof. Vyacheslav Futorny 1 a parte: Resolução de sistemas de equações lineares, matrizes inversíveis 1. Para cada um dos seguintes sistemas de equações
1 a Lista de Exercícios MAT 3211 Álgebra Linear - 213 - Prof. Vyacheslav Futorny 1 a parte: Resolução de sistemas de equações lineares, matrizes inversíveis 1. Para cada um dos seguintes sistemas de equações
MAT Álgebra Linear para Engenharia II - Poli 2 ō semestre de ā Lista de Exercícios
 MAT 2458 - Álgebra Linear para Engenharia II - Poli 2 ō semestre de 2014 1 ā Lista de Exercícios 1. Verifique se V = {(x, y) x, y R} é um espaço vetorial sobre R com as operações de adição e de multiplicação
MAT 2458 - Álgebra Linear para Engenharia II - Poli 2 ō semestre de 2014 1 ā Lista de Exercícios 1. Verifique se V = {(x, y) x, y R} é um espaço vetorial sobre R com as operações de adição e de multiplicação
Aula 25 - Espaços Vetoriais
 Espaço Vetorial: Aula 25 - Espaços Vetoriais Seja V um conjunto não vazio de objetos com duas operações definidas: 1. Uma adição que associa a cada par de objetos u, v em V um único objeto u + v, denominado
Espaço Vetorial: Aula 25 - Espaços Vetoriais Seja V um conjunto não vazio de objetos com duas operações definidas: 1. Uma adição que associa a cada par de objetos u, v em V um único objeto u + v, denominado
Segunda prova de Álgebra Linear Aplicada - 20/02/2013 Prof. Juliana Coelho - 07h00-09h00
 Segunda prova de Álgebra Linear Aplicada - 20/02/2013 Prof Juliana Coelho - 07h00-09h00 QUESTÃO 1 (2,0 pts - Considere os seguintes vetores de R3 : u = (3, 2, 2, v = (1, 3, 1 e w = ( 1, 4, 4 Responda as
Segunda prova de Álgebra Linear Aplicada - 20/02/2013 Prof Juliana Coelho - 07h00-09h00 QUESTÃO 1 (2,0 pts - Considere os seguintes vetores de R3 : u = (3, 2, 2, v = (1, 3, 1 e w = ( 1, 4, 4 Responda as
Soluções dos trabalhos de 1 a 7
 Universidade Federal Rural do Semiárido-UFERSA Departamento de Ciências Exatas e Naturais Curso: Bacharelado em Ciência e Tecnologia e Computação Disciplina: Álgebra Linear Aluno(a): Soluções dos trabalhos
Universidade Federal Rural do Semiárido-UFERSA Departamento de Ciências Exatas e Naturais Curso: Bacharelado em Ciência e Tecnologia e Computação Disciplina: Álgebra Linear Aluno(a): Soluções dos trabalhos
(x 1, y 1 ) (x 2, y 2 ) = (x 1 x 2, y 1 y 2 ); e α (x, y) = (x α, y α ), α R.
 INSTITUTO DE MATEMÁTICA E ESTATÍSTICA UNIVERSIDADE DE SÃO PAULO MAT-2457 Álgebra Linear para Engenharia I Terceira Lista de Exercícios - Professor: Equipe da Disciplina EXERCÍCIOS 1. Considere as retas
INSTITUTO DE MATEMÁTICA E ESTATÍSTICA UNIVERSIDADE DE SÃO PAULO MAT-2457 Álgebra Linear para Engenharia I Terceira Lista de Exercícios - Professor: Equipe da Disciplina EXERCÍCIOS 1. Considere as retas
5. Considere os seguintes subconjuntos do espaço vetorial F(R) das funções de R em R:
 MAT3457 ÁLGEBRA LINEAR I 3 a Lista de Exercícios 1 o semestre de 2018 1. Verique se V = {(x, y) : x, y R} é um espaço vetorial sobre R com as operações de adição e de multiplicação por escalar dadas por:
MAT3457 ÁLGEBRA LINEAR I 3 a Lista de Exercícios 1 o semestre de 2018 1. Verique se V = {(x, y) : x, y R} é um espaço vetorial sobre R com as operações de adição e de multiplicação por escalar dadas por:
Álgebra Linear - 2 a lista de exercícios Prof. - Juliana Coelho
 Álgebra Linear - 2 a lista de exercícios Prof. - Juliana Coelho 1 - Verifique que os conjuntos V abaixo com as operações dadas não são espaços vetoriais explicitando a falha em alguma das propriedades.
Álgebra Linear - 2 a lista de exercícios Prof. - Juliana Coelho 1 - Verifique que os conjuntos V abaixo com as operações dadas não são espaços vetoriais explicitando a falha em alguma das propriedades.
6. Verifique detalhadamente que os seguintes conjuntos são espaços vetoriais(com a soma e produto por escalar usuais):
 a Lista. Sejam u = ( 4 ) v = ( 5) e w = (a b). Encontre a e b tais que (a)w = u + v (b)w = 5v (c)u + w = u v. Represente os vetores acima no plano cartesiano.. Sejam u = (4 ) v = ( 4) e w = (a b c). Encontre
a Lista. Sejam u = ( 4 ) v = ( 5) e w = (a b). Encontre a e b tais que (a)w = u + v (b)w = 5v (c)u + w = u v. Represente os vetores acima no plano cartesiano.. Sejam u = (4 ) v = ( 4) e w = (a b c). Encontre
ÁLGEBRA LINEAR I - MAT Em cada item diga se a afirmação é verdadeira ou falsa. Justifiquei sua resposta.
 UNIVERSIDADE FEDERAL DA INTEGRAÇÃO LATINO-AMERICANA Instituto Latino-Americano de Ciências da Vida e Da Natureza Centro Interdisciplinar de Ciências da Natureza ÁLGEBRA LINEAR I - MAT0032 2 a Lista de
UNIVERSIDADE FEDERAL DA INTEGRAÇÃO LATINO-AMERICANA Instituto Latino-Americano de Ciências da Vida e Da Natureza Centro Interdisciplinar de Ciências da Natureza ÁLGEBRA LINEAR I - MAT0032 2 a Lista de
Curso de Álgebra Linear
 Curso de Álgebra Linear Fundamentos e Aplicações Terceira Edição 25 de Outubro de 2012 Marco Cabral PhD Indiana University, EUA Paulo Goldfeld PhD Courant Institute, EUA Departamento de Matemática Aplicada
Curso de Álgebra Linear Fundamentos e Aplicações Terceira Edição 25 de Outubro de 2012 Marco Cabral PhD Indiana University, EUA Paulo Goldfeld PhD Courant Institute, EUA Departamento de Matemática Aplicada
ESPAÇO VETORIAL REAL. b) Em relação à multiplicação: (ab) v = a(bv) (a + b) v = av + bv a (u + v ) = au + av 1u = u, para u, v V e a, b R
 ESPAÇO VETORIAL REAL Seja um conjunto V, não vazio, sobre o qual estão definidas as operações de adição e multiplicação por escalar, isto é: u, v V, u + v V a R, u V, au V O conjunto V com estas duas operações
ESPAÇO VETORIAL REAL Seja um conjunto V, não vazio, sobre o qual estão definidas as operações de adição e multiplicação por escalar, isto é: u, v V, u + v V a R, u V, au V O conjunto V com estas duas operações
Universidade Federal de Viçosa Centro de Ciências Exatas e Tecnológicas Departamento de Matemática
 1 Universidade Federal de Viçosa Centro de Ciências Exatas e Tecnológicas Departamento de Matemática 3 a Lista - MAT 137 - Introdução à Álgebra Linear 2017/II 1. Sejam u = ( 4 3) v = (2 5) e w = (a b).
1 Universidade Federal de Viçosa Centro de Ciências Exatas e Tecnológicas Departamento de Matemática 3 a Lista - MAT 137 - Introdução à Álgebra Linear 2017/II 1. Sejam u = ( 4 3) v = (2 5) e w = (a b).
MA71B - Geometria Analítica e Álgebra Linear Profa. Dra. Diane Rizzotto Rossetto. LISTA 5 - Espaços Vetoriais
 Ministério da Educação Universidade Tecnológica Federal do Paraná Campus Curitiba - DAMAT MA7B - Geometria Analítica e Álgebra Linear Profa. Dra. Diane Rizzotto Rossetto LISTA 5 - Espaços Vetoriais Desenvolvidas
Ministério da Educação Universidade Tecnológica Federal do Paraná Campus Curitiba - DAMAT MA7B - Geometria Analítica e Álgebra Linear Profa. Dra. Diane Rizzotto Rossetto LISTA 5 - Espaços Vetoriais Desenvolvidas
Questão 1: Seja V o conjunto de todos os pares ordenados de números reais. Denamos a adição e a multiplicação por escalar em V por
 Ministério da Educação Universidade Tecnológica Federal do Paraná Campus Curitiba - DAMAT MA7B - Geometria Analítica e Álgebra Linear Profa. Dra. Diane Rizzotto Rossetto LISTA 4 - Espaços Vetoriais Desenvolvidas
Ministério da Educação Universidade Tecnológica Federal do Paraná Campus Curitiba - DAMAT MA7B - Geometria Analítica e Álgebra Linear Profa. Dra. Diane Rizzotto Rossetto LISTA 4 - Espaços Vetoriais Desenvolvidas
1. Conhecendo-se somente os produtos AB e AC, calcule A = X 2 = 2X. 3. Mostre que se A e B são matrizes que comutam com a matriz M = 1 0
 Lista de exercícios. AL. 1 sem. 2015 Prof. Fabiano Borges da Silva 1 Matrizes Notações: 0 para matriz nula; I para matriz identidade; 1. Conhecendo-se somente os produtos AB e AC calcule A(B + C) B t A
Lista de exercícios. AL. 1 sem. 2015 Prof. Fabiano Borges da Silva 1 Matrizes Notações: 0 para matriz nula; I para matriz identidade; 1. Conhecendo-se somente os produtos AB e AC calcule A(B + C) B t A
Espaços Euclidianos. Espaços R n. O conjunto R n é definido como o conjunto de todas as n-uplas ordenadas de números reais:
 Espaços Euclidianos Espaços R n O conjunto R n é definido como o conjunto de todas as n-uplas ordenadas de números reais: R n = {(x 1,..., x n ) : x 1,..., x n R}. R 1 é simplesmente o conjunto R dos números
Espaços Euclidianos Espaços R n O conjunto R n é definido como o conjunto de todas as n-uplas ordenadas de números reais: R n = {(x 1,..., x n ) : x 1,..., x n R}. R 1 é simplesmente o conjunto R dos números
Primeira Lista de Exercícios
 1 Espaços vetoriais Primeira Lista de Exercícios {( ) } a b Exercício 1.1. Considere M 2 := : a, b, c, d R, : M c d 2 M 2 M 2 dada por e : R M 2 M 2 dada por ( ) ( ) ( ) a1 b 1 a2 b 2 a1 + a := 2 b 1 +
1 Espaços vetoriais Primeira Lista de Exercícios {( ) } a b Exercício 1.1. Considere M 2 := : a, b, c, d R, : M c d 2 M 2 M 2 dada por e : R M 2 M 2 dada por ( ) ( ) ( ) a1 b 1 a2 b 2 a1 + a := 2 b 1 +
Interbits SuperPro Web
 1 (Ita 018) Uma progressão aritmética (a 1, a,, a n) satisfaz a propriedade: para cada n, a soma da progressão é igual a n 5n Nessas condições, o determinante da matriz a1 a a a4 a5 a 6 a a a 7 8 9 a)
1 (Ita 018) Uma progressão aritmética (a 1, a,, a n) satisfaz a propriedade: para cada n, a soma da progressão é igual a n 5n Nessas condições, o determinante da matriz a1 a a a4 a5 a 6 a a a 7 8 9 a)
Exercícios sobre Espaços Vetoriais II
 Exercícios sobre Espaços Vetoriais II Prof.: Alonso Sepúlveda Castellanos Sala 1F 104 1. Seja V um espaço vetorial não trivial sobre um corpo infinito. Mostre que V contém infinitos elementos. 2. Sejam
Exercícios sobre Espaços Vetoriais II Prof.: Alonso Sepúlveda Castellanos Sala 1F 104 1. Seja V um espaço vetorial não trivial sobre um corpo infinito. Mostre que V contém infinitos elementos. 2. Sejam
Álgebra Linear AL. Luiza Amalia Pinto Cantão. Depto. de Engenharia Ambiental Universidade Estadual Paulista UNESP
 Álgebra Linear AL Luiza Amalia Pinto Cantão Depto de Engenharia Ambiental Universidade Estadual Paulista UNESP luiza@sorocabaunespbr Espaços Vetoriais 1 Definição; 2 Subespaços; 3 Combinação Linear, dependência
Álgebra Linear AL Luiza Amalia Pinto Cantão Depto de Engenharia Ambiental Universidade Estadual Paulista UNESP luiza@sorocabaunespbr Espaços Vetoriais 1 Definição; 2 Subespaços; 3 Combinação Linear, dependência
Notas para o Curso de Algebra Linear Il Dayse Haime Pastore 20 de fevereiro de 2009
 Notas para o Curso de Álgebra Linear Il Dayse Haime Pastore 20 de fevereiro de 2009 2 Sumário 1 Matrizes e Sistemas Lineares 5 11 Matrizes 6 12 Sistemas Lineares 11 121 Eliminação Gaussiana 12 122 Resolução
Notas para o Curso de Álgebra Linear Il Dayse Haime Pastore 20 de fevereiro de 2009 2 Sumário 1 Matrizes e Sistemas Lineares 5 11 Matrizes 6 12 Sistemas Lineares 11 121 Eliminação Gaussiana 12 122 Resolução
UFPB - CCEN - DEPARTAMENTO DE MATEMÁTICA ÁLGEBRA LINEAR E GEOMETRIA ANALÍTICA 1 a LISTA DE EXERCÍCIOS PERÍODO
 UFPB - CCEN - DEPARTAMENTO DE MATEMÁTICA ÁLGEBRA LINEAR E GEOMETRIA ANALÍTICA a LISTA DE EXERCÍCIOS PERÍODO 0 Os exercícios 0 8 trazem um espaço vetorial V e um seu subconjunto W Sempre que W for um subespaço
UFPB - CCEN - DEPARTAMENTO DE MATEMÁTICA ÁLGEBRA LINEAR E GEOMETRIA ANALÍTICA a LISTA DE EXERCÍCIOS PERÍODO 0 Os exercícios 0 8 trazem um espaço vetorial V e um seu subconjunto W Sempre que W for um subespaço
1. Não temos um espaço vetorial, pois a seguinte propriedade (a + b) v = a v + b v não vale. De fato:
 Sumário No que se segue, C, R, Q, Z, N denotam respectivamente, o conjunto dos números complexos, reais, racionais, inteiros e naturais. Denotaremos por I (ou id) End(V ) a função identidade do espaço
Sumário No que se segue, C, R, Q, Z, N denotam respectivamente, o conjunto dos números complexos, reais, racionais, inteiros e naturais. Denotaremos por I (ou id) End(V ) a função identidade do espaço
Álgebra Linear e Geometria Anaĺıtica. Espaços Vetoriais Reais
 universidade de aveiro departamento de matemática Álgebra Linear e Geometria Anaĺıtica Agrupamento IV (ECT, EET, EI) Capítulo 4 Espaços Vetoriais Reais Definição de espaço vetorial real [4 01] O conjunto
universidade de aveiro departamento de matemática Álgebra Linear e Geometria Anaĺıtica Agrupamento IV (ECT, EET, EI) Capítulo 4 Espaços Vetoriais Reais Definição de espaço vetorial real [4 01] O conjunto
Álgebra linear A Primeira lista de exercícios
 Álgebra linear A Primeira lista de exercícios Prof. Edivaldo L. dos Santos (1) Verifique, em cada um dos itens abaixo, se o conjunto V com as operações indicadas é um espaço vetorial sobre R. {[ ] a b
Álgebra linear A Primeira lista de exercícios Prof. Edivaldo L. dos Santos (1) Verifique, em cada um dos itens abaixo, se o conjunto V com as operações indicadas é um espaço vetorial sobre R. {[ ] a b
Segunda prova de Álgebra Linear Aplicada - 20/02/2013 Prof. Juliana Coelho - 11h00-13h00
 Segunda prova de Álgebra Linear Aplicada - 20/02/2013 Prof. Juliana Coelho - 11h00-13h00 QUESTÃO 1 (1,2 pts) - Determine os valores de a R para os quais os vetores u = (1, 0, a), v = ( 2, 1, 0) e w = (a,
Segunda prova de Álgebra Linear Aplicada - 20/02/2013 Prof. Juliana Coelho - 11h00-13h00 QUESTÃO 1 (1,2 pts) - Determine os valores de a R para os quais os vetores u = (1, 0, a), v = ( 2, 1, 0) e w = (a,
Parte 2 - Espaços Vetoriais
 Espaço Vetorial: Parte 2 - Espaços Vetoriais Seja V um conjunto não vazio de objetos com duas operações definidas: 1. Uma adição que associa a cada par de objetos u, v em V um único objeto u + v, denominado
Espaço Vetorial: Parte 2 - Espaços Vetoriais Seja V um conjunto não vazio de objetos com duas operações definidas: 1. Uma adição que associa a cada par de objetos u, v em V um único objeto u + v, denominado
Primeira prova de Álgebra Linear - 06/05/2011 Prof. - Juliana Coelho
 Primeira prova de Álgebra Linear - 6/5/211 Prof. - Juliana Coelho JUSTIFIQUE SUAS RESPOSTAS! Questões contendo só a resposta, sem desenvolvimento ou justificativa serão desconsideradas! QUESTÃO 1 (2, pts)
Primeira prova de Álgebra Linear - 6/5/211 Prof. - Juliana Coelho JUSTIFIQUE SUAS RESPOSTAS! Questões contendo só a resposta, sem desenvolvimento ou justificativa serão desconsideradas! QUESTÃO 1 (2, pts)
1 a Lista de Exercícios de MAT3458 Escola Politécnica 2 o semestre de 2016
 1 a Lista de Exercícios de MAT3458 Escola Politécnica o semestre de 16 1 Para que valores de t R a função definida por (x 1, x ), (y 1, y ) = x 1 y 1 + tx y é um produto interno em R? Para cada par de
1 a Lista de Exercícios de MAT3458 Escola Politécnica o semestre de 16 1 Para que valores de t R a função definida por (x 1, x ), (y 1, y ) = x 1 y 1 + tx y é um produto interno em R? Para cada par de
CM005 Algebra Linear Lista 1
 CM005 Algebra Linear Lista Alberto Ramos. Para cada um dos sistemas de equações lineares, use o método de Gauss para obter um sistema equivalente cuja matriz de coeficientes esteja na forma escada. Indique
CM005 Algebra Linear Lista Alberto Ramos. Para cada um dos sistemas de equações lineares, use o método de Gauss para obter um sistema equivalente cuja matriz de coeficientes esteja na forma escada. Indique
UNIVERSIDADE FEDERAL DE VIÇOSA Centro de Ciências Exatas Departamento de Matemática
 UNIVERSIDADE FEDERAL DE VIÇOSA Centro de Ciências Exatas Departamento de Matemática 2 a Lista - MAT 137 - Introdução à Álgebra Linear II/2005 1 Resolva os seguintes sistemas lineares utilizando o Método
UNIVERSIDADE FEDERAL DE VIÇOSA Centro de Ciências Exatas Departamento de Matemática 2 a Lista - MAT 137 - Introdução à Álgebra Linear II/2005 1 Resolva os seguintes sistemas lineares utilizando o Método
ÁLGEBRA LINEAR I - MAT Determinar se os seguintes conjuntos são linearmente dependente ou linearmente independente (R).
 UNIVERSIDADE FEDERAL DA INTEGRAÇÃO LATINO-AMERICANA Instituto Latino-Americano de Ciências da Vida e Da Natureza Centro Interdisciplinar de Ciências da Natureza ÁLGEBRA LINEAR I - MAT0032 3 a Lista de
UNIVERSIDADE FEDERAL DA INTEGRAÇÃO LATINO-AMERICANA Instituto Latino-Americano de Ciências da Vida e Da Natureza Centro Interdisciplinar de Ciências da Natureza ÁLGEBRA LINEAR I - MAT0032 3 a Lista de
Álgebra Linear
 Álgebra Linear - 0191 Lista 3 - Dependência e Independência Linear Bases e Soma Direta 1) Exiba três vetores u v w R 3 com as seguintes propriedades: nenhum deles é múltiplo do outro nenhuma das coordenadas
Álgebra Linear - 0191 Lista 3 - Dependência e Independência Linear Bases e Soma Direta 1) Exiba três vetores u v w R 3 com as seguintes propriedades: nenhum deles é múltiplo do outro nenhuma das coordenadas
Tópicos de Álgebra Linear Verão 2019 Lista 1: Espaços Vetoriais
 Universidade Federal do Paraná Centro Politécnico ET-DMAT Prof. Maria Eugênia Martin Tópicos de Álgebra Linear Verão 2019 Lista 1: Espaços Vetoriais Exercício 1. Determine se os seguintes conjuntos são
Universidade Federal do Paraná Centro Politécnico ET-DMAT Prof. Maria Eugênia Martin Tópicos de Álgebra Linear Verão 2019 Lista 1: Espaços Vetoriais Exercício 1. Determine se os seguintes conjuntos são
exercícios de álgebra linear 2016
 exercícios de álgebra linear 206 maria irene falcão :: maria joana soares Conteúdo Matrizes 2 Sistemas de equações lineares 7 3 Determinantes 3 4 Espaços vetoriais 9 5 Transformações lineares 27 6 Valores
exercícios de álgebra linear 206 maria irene falcão :: maria joana soares Conteúdo Matrizes 2 Sistemas de equações lineares 7 3 Determinantes 3 4 Espaços vetoriais 9 5 Transformações lineares 27 6 Valores
Universidade Federal de Viçosa Centro de Ciências Exatas e Tecnológicas Departamento de Matemática
 1 Universidade Federal de Viçosa Centro de Ciências Exatas e Tecnológicas Departamento de Matemática Lista 4 - MAT 137 -Introdução à Álgebra Linear 2017/II 1. Entre as funções dadas abaixo, verifique quais
1 Universidade Federal de Viçosa Centro de Ciências Exatas e Tecnológicas Departamento de Matemática Lista 4 - MAT 137 -Introdução à Álgebra Linear 2017/II 1. Entre as funções dadas abaixo, verifique quais
Álgebra Linear Semana 05
 Álgebra Linear Semana 5 Diego Marcon 4 de Abril de 7 Conteúdo Interpretações de sistemas lineares e de matrizes invertíveis Caracterizações de matrizes invertíveis 4 Espaços vetoriais 5 Subespaços vetoriais
Álgebra Linear Semana 5 Diego Marcon 4 de Abril de 7 Conteúdo Interpretações de sistemas lineares e de matrizes invertíveis Caracterizações de matrizes invertíveis 4 Espaços vetoriais 5 Subespaços vetoriais
2 Espaços Vetoriais. 2.1 Espaços Vetoriais Euclidianos
 2 Espaços Vetoriais 2.1 Espaços Vetoriais Euclidianos Definição: Dado n N, considere-se o conjunto de todos os n-uplos ordenados de elementos reais, isto é o conjunto de elementos da forma x = (x 1,, x
2 Espaços Vetoriais 2.1 Espaços Vetoriais Euclidianos Definição: Dado n N, considere-se o conjunto de todos os n-uplos ordenados de elementos reais, isto é o conjunto de elementos da forma x = (x 1,, x
(d) Seja W um espaço vetorial de dimensão 4 e sejam U e V subespaços de W tais que U V = 0. Assinale. Gabarito Pág. 1
 UFRJ Instituto de Matemática Disciplina: Algebra Linear II - MAE 125 Professor: Bruno, Gregório, Luiz Carlos, Mario, Milton, Monique e Umberto Data: 15 de maio de 2013 Primeira Prova 1. Os valores de (a,
UFRJ Instituto de Matemática Disciplina: Algebra Linear II - MAE 125 Professor: Bruno, Gregório, Luiz Carlos, Mario, Milton, Monique e Umberto Data: 15 de maio de 2013 Primeira Prova 1. Os valores de (a,
. (1) Se S é o espaço vetorial gerado pelos vetores 1 e,0,1
 QUESTÕES ANPEC ÁLGEBRA LINEAR QUESTÃO 0 Assinale V (verdadeiro) ou F (falso): (0) Os vetores (,, ) (,,) e (, 0,) formam uma base de,, o espaço vetorial gerado por,, e,, passa pela origem na direção de,,
QUESTÕES ANPEC ÁLGEBRA LINEAR QUESTÃO 0 Assinale V (verdadeiro) ou F (falso): (0) Os vetores (,, ) (,,) e (, 0,) formam uma base de,, o espaço vetorial gerado por,, e,, passa pela origem na direção de,,
Q1. Seja V um espaço vetorial e considere as seguintes afirmações: um conjunto de geradores de um subespaço S 2 de V, então A 1 A 2
 Q1. Seja V um espaço vetorial e considere as seguintes afirmações: (I) se A 1 é um conjunto de geradores de um subespaço S 1 de V e A 2 é um conjunto de geradores de um subespaço S 2 de V, então A 1 A
Q1. Seja V um espaço vetorial e considere as seguintes afirmações: (I) se A 1 é um conjunto de geradores de um subespaço S 1 de V e A 2 é um conjunto de geradores de um subespaço S 2 de V, então A 1 A
MINISTÉRIO DA EDUCAÇÃO E DO DESPORTO UNIVERSIDADE FEDERAL DE VIÇOSA DEPARTAMENTO DE MATEMÁTICA
 MINISTÉRIO DA EDUCAÇÃO E DO DESPORTO UNIVERSIDADE FEDERAL DE VIÇOSA DEPARTAMENTO DE MATEMÁTICA a LISTA DE EXERCÍCIOS DE MAT 7 II SEMESTRE DE 00 Professores: Flávia, Gustavo e Lana. Suponha que uma força
MINISTÉRIO DA EDUCAÇÃO E DO DESPORTO UNIVERSIDADE FEDERAL DE VIÇOSA DEPARTAMENTO DE MATEMÁTICA a LISTA DE EXERCÍCIOS DE MAT 7 II SEMESTRE DE 00 Professores: Flávia, Gustavo e Lana. Suponha que uma força
MAT2457 ÁLGEBRA LINEAR PARA ENGENHARIA I 3 a Prova - 1 o semestre de (a) 3; (b) 2; (c) 0; (d) 1; (e) 2.
 MAT2457 ÁLGEBRA LINEAR PARA ENGENHARIA I 3 a Prova - 1 o semestre de 2018 Questão 1. Seja U = [(2, 1, 1), (1, 0, 2)], subespaço vetorial de R 3 e ax + by + z = 0 uma equação de U, isto é U = { (x, y, z)
MAT2457 ÁLGEBRA LINEAR PARA ENGENHARIA I 3 a Prova - 1 o semestre de 2018 Questão 1. Seja U = [(2, 1, 1), (1, 0, 2)], subespaço vetorial de R 3 e ax + by + z = 0 uma equação de U, isto é U = { (x, y, z)
Aulas práticas de Álgebra Linear
 Ficha 3 Aulas práticas de Álgebra Linear Licenciatura em Engenharia Naval e Oceânica Mestrado Integrado em Engenharia Mecânica 1 o semestre 2018/19 Jorge Almeida e Lina Oliveira Departamento de Matemática,
Ficha 3 Aulas práticas de Álgebra Linear Licenciatura em Engenharia Naval e Oceânica Mestrado Integrado em Engenharia Mecânica 1 o semestre 2018/19 Jorge Almeida e Lina Oliveira Departamento de Matemática,
MAT Resumo Teórico e Lista de
 MAT 0132 - Resumo Teórico e Lista de Exercícios April 10, 2005 1 Vetores Geométricos Livres 1.1 Construção dos Vetores 1.2 Adição de Vetores 1.3 Multiplicação de um Vetor por um Número Real 2 Espaços Vetoriais
MAT 0132 - Resumo Teórico e Lista de Exercícios April 10, 2005 1 Vetores Geométricos Livres 1.1 Construção dos Vetores 1.2 Adição de Vetores 1.3 Multiplicação de um Vetor por um Número Real 2 Espaços Vetoriais
Lista de exercícios 8 Bases e Dimensão.
 Universidade Federal do Paraná semestre 05. Algebra Linear, CM 005 Olivier Brahic Lista de exercícios 8 Bases e Dimensão. Exercício : No exercício da Folha 7, indique se os vetores formam uma base para
Universidade Federal do Paraná semestre 05. Algebra Linear, CM 005 Olivier Brahic Lista de exercícios 8 Bases e Dimensão. Exercício : No exercício da Folha 7, indique se os vetores formam uma base para
Álgebra Linear. Professor Alessandro Monteiro. 1º Sábado - Matrizes - 11/03/2017
 º Sábado - Matrizes - //7. Plano e Programa de Ensino. Matrizes. Exemplos. Ordem de Uma Matriz. Exemplos. Representação 7. Matriz Genérica m x n 8. Matriz Linha 9. Exemplos. Matriz Coluna. Exemplos. Diagonal
º Sábado - Matrizes - //7. Plano e Programa de Ensino. Matrizes. Exemplos. Ordem de Uma Matriz. Exemplos. Representação 7. Matriz Genérica m x n 8. Matriz Linha 9. Exemplos. Matriz Coluna. Exemplos. Diagonal
MINISTÉRIO DA EDUCAÇÃO E DO DESPORTO UNIVERSIDADE FEDERAL DE VIÇOSA DEPARTAMENTO DE MATEMÁTICA
 MINISTÉRIO DA EDUCAÇÃO E DO DESPORTO UNIVERSIDADE FEDERAL DE VIÇOSA DEPARTAMENTO DE MATEMÁTICA 1 a LISTA DE EXERCÍCIOS DE MAT 17 1. Suponha que uma força de 1 newtons é aplicada em um objeto ao longo do
MINISTÉRIO DA EDUCAÇÃO E DO DESPORTO UNIVERSIDADE FEDERAL DE VIÇOSA DEPARTAMENTO DE MATEMÁTICA 1 a LISTA DE EXERCÍCIOS DE MAT 17 1. Suponha que uma força de 1 newtons é aplicada em um objeto ao longo do
Lista de exercícios 6 Espaços Vetoriais
 Universidade Federal do Paraná semestre 016. Algebra Linear, Olivier Brahic Lista de exercícios 6 Espaços Vetoriais Exercícios da Seção 3. Exercício 1: Determine se os seguintes conjuntos formam subespaços
Universidade Federal do Paraná semestre 016. Algebra Linear, Olivier Brahic Lista de exercícios 6 Espaços Vetoriais Exercícios da Seção 3. Exercício 1: Determine se os seguintes conjuntos formam subespaços
Álgebra Linear e Geometria Analítica
 Instituto Politécnico de Viseu Escola Superior de Tecnologia Departamento: Matemática Álgebra Linear e Geometria Analítica Curso: Engenharia Electrotécnica Ano: 1 o Semestre: 1 o Ano Lectivo: 007/008 Ficha
Instituto Politécnico de Viseu Escola Superior de Tecnologia Departamento: Matemática Álgebra Linear e Geometria Analítica Curso: Engenharia Electrotécnica Ano: 1 o Semestre: 1 o Ano Lectivo: 007/008 Ficha
Lista de Álgebra Linear Aplicada
 Lista de Álgebra Linear Aplicada Matrizes - Vetores - Retas e Planos 3 de setembro de 203 Professor: Aldo Bazán Universidade Federal Fluminense Matrizes. Seja A M 2 2 (R) definida como 0 0 0 3 0 0 0 2
Lista de Álgebra Linear Aplicada Matrizes - Vetores - Retas e Planos 3 de setembro de 203 Professor: Aldo Bazán Universidade Federal Fluminense Matrizes. Seja A M 2 2 (R) definida como 0 0 0 3 0 0 0 2
Método prático para extrair uma base de um conjunto de geradores de um subespaço de R n
 Método prático para extrair uma base de um conjunto de geradores de um subespaço de R n 1. Descrição do método e alguns exemplos Colocamos o seguinte problema: dado um conjunto finito: A = {a 1, a 2,...,
Método prático para extrair uma base de um conjunto de geradores de um subespaço de R n 1. Descrição do método e alguns exemplos Colocamos o seguinte problema: dado um conjunto finito: A = {a 1, a 2,...,
ÁLGEBRA LINEAR. Base e Dimensão de um Espaço Vetorial. Prof. Susie C. Keller
 ÁLGEBRA LINEAR Base e Dimensão de um Espaço Vetorial Prof. Susie C. Keller Base de um Espaço Vetorial Um conjunto B = {v 1,..., v n } V é uma base do espaço vetorial V se: I) B é LI II) B gera V Base de
ÁLGEBRA LINEAR Base e Dimensão de um Espaço Vetorial Prof. Susie C. Keller Base de um Espaço Vetorial Um conjunto B = {v 1,..., v n } V é uma base do espaço vetorial V se: I) B é LI II) B gera V Base de
ALGEBRA LINEAR 1 RESUMO E EXERCÍCIOS* P1
 ALGEBRA LINEAR 1 RESUMO E EXERCÍCIOS* P1 *Exercícios de provas anteriores escolhidos para você estar preparado para qualquer questão na prova. Resoluções em VETORES Um vetor é uma lista ordenada de números
ALGEBRA LINEAR 1 RESUMO E EXERCÍCIOS* P1 *Exercícios de provas anteriores escolhidos para você estar preparado para qualquer questão na prova. Resoluções em VETORES Um vetor é uma lista ordenada de números
II Lista de Álgebra Linear /02 Espaços Vetoriais Prof. Iva Zuchi Siple
 . Verique se R com as operações denidas por: II Lista de Álgebra Linear - / Espaços Vetoriais Prof. Iva Zuchi Siple i. (x y) + (s t) (s y + t) onde u (x y) e v (s t) pertencem a R ii. α(x y) (αx y) onde
. Verique se R com as operações denidas por: II Lista de Álgebra Linear - / Espaços Vetoriais Prof. Iva Zuchi Siple i. (x y) + (s t) (s y + t) onde u (x y) e v (s t) pertencem a R ii. α(x y) (αx y) onde
Renato Martins Assunção
 Análise Numérica Renato Martins Assunção DCC - UFMG 2012 Renato Martins Assunção (DCC - UFMG) Análise Numérica 2012 1 / 84 Equação linear Sistemas de equações lineares A equação 2x + 3y = 6 é chamada linear
Análise Numérica Renato Martins Assunção DCC - UFMG 2012 Renato Martins Assunção (DCC - UFMG) Análise Numérica 2012 1 / 84 Equação linear Sistemas de equações lineares A equação 2x + 3y = 6 é chamada linear
Universidade Federal Fluminense - GAN
 Solimá Gomes Pimentel Universidade Federal Fluminense IM - GAN Solimá Gomes Pimentel, ****- Matemática para Economia III/Solimá Gomes Pimentel 2pt, ; 31cm Inclui Bibliografia. 1. Matemática para Economia
Solimá Gomes Pimentel Universidade Federal Fluminense IM - GAN Solimá Gomes Pimentel, ****- Matemática para Economia III/Solimá Gomes Pimentel 2pt, ; 31cm Inclui Bibliografia. 1. Matemática para Economia
Álgebra Linear. André Arbex Hallack
 Álgebra Linear André Arbex Hallack 2017 Índice 1 Sistemas Lineares 1 1.1 Corpos............................................. 1 1.2 Sistemas de Equações Lineares............................... 3 1.3 Sistemas
Álgebra Linear André Arbex Hallack 2017 Índice 1 Sistemas Lineares 1 1.1 Corpos............................................. 1 1.2 Sistemas de Equações Lineares............................... 3 1.3 Sistemas
(x 1 + iy 1 ) + (x 2 + iy 2 ) = x 1 + x 2 + i(y 1 + y 2 ) a(x + iy) = ax + i(ay)
 Espaços Vetoriais Definição. Um espaço vetorial sobre R é um conjunto V no qual se tem definida uma adição e uma multiplicação de seus elementos por escalares (isto é, por números reais), ou seja, dados
Espaços Vetoriais Definição. Um espaço vetorial sobre R é um conjunto V no qual se tem definida uma adição e uma multiplicação de seus elementos por escalares (isto é, por números reais), ou seja, dados
Álgebra Linear Exercícios Resolvidos
 Álgebra Linear Exercícios Resolvidos Agosto de 001 Sumário 1 Exercícios Resolvidos Uma Revisão 5 Mais Exercícios Resolvidos Sobre Transformações Lineares 13 3 4 SUMA RIO Capítulo 1 Exercícios Resolvidos
Álgebra Linear Exercícios Resolvidos Agosto de 001 Sumário 1 Exercícios Resolvidos Uma Revisão 5 Mais Exercícios Resolvidos Sobre Transformações Lineares 13 3 4 SUMA RIO Capítulo 1 Exercícios Resolvidos
Universidade Federal de Uberlândia Faculdade de Matemática
 Universidade Federal de Uberlândia Faculdade de Matemática Universidade Federal de Uberlândia Faculdade de Matemática Disciplina : Geometria Analítica e Álgebra Linear - GCI004 Assunto: Espaços vetoriais
Universidade Federal de Uberlândia Faculdade de Matemática Universidade Federal de Uberlândia Faculdade de Matemática Disciplina : Geometria Analítica e Álgebra Linear - GCI004 Assunto: Espaços vetoriais
I Lista de Álgebra Linear /02 Matrizes-Determinantes e Sistemas Prof. Iva Zuchi Siple
 1 I Lista de Álgebra Linear - 2012/02 Matrizes-Determinantes e Sistemas Prof. Iva Zuchi Siple 1. Determine os valores de x e y que tornam verdadeira a igualdade ( x 2 + 5x x 2 ( 6 3 2x y 2 5y y 2 = 5 0
1 I Lista de Álgebra Linear - 2012/02 Matrizes-Determinantes e Sistemas Prof. Iva Zuchi Siple 1. Determine os valores de x e y que tornam verdadeira a igualdade ( x 2 + 5x x 2 ( 6 3 2x y 2 5y y 2 = 5 0
GAAL Exercícios 6: Umas soluções
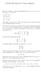 GAAL Exercícios 6: Umas soluções. Quais dos seguintes vetores são combinação linear de u = (5, 3, ), v = (, 4, 3), w = (, 8, 7)? (a) (, 2, 5) (b) (, 2, 8) (c) ( 2, ) (d) (, 2, 3). O conjunto {u, v, w}
GAAL Exercícios 6: Umas soluções. Quais dos seguintes vetores são combinação linear de u = (5, 3, ), v = (, 4, 3), w = (, 8, 7)? (a) (, 2, 5) (b) (, 2, 8) (c) ( 2, ) (d) (, 2, 3). O conjunto {u, v, w}
MAT2458 ÁLGEBRA LINEAR PARA ENGENHARIA II 2 a Prova - 2 o semestre de T ( p(x) ) = p(x + 1) p(x), (a) 8, (b) 5, (c) 0, (d) 3, (e) 4.
 MAT2458 ÁLGEBRA LINEAR PARA ENGENHARIA II 2 a Prova - 2 o semestre de 218 Q1. Considere a transformação linear T : P 3 (R) P 2 (R), dada por T ( p(x) ) = p(x + 1) p(x), para todo p(x) P 3 (R), e seja A
MAT2458 ÁLGEBRA LINEAR PARA ENGENHARIA II 2 a Prova - 2 o semestre de 218 Q1. Considere a transformação linear T : P 3 (R) P 2 (R), dada por T ( p(x) ) = p(x + 1) p(x), para todo p(x) P 3 (R), e seja A
2 a. Lista de Exercícios
 Última atualização 16/09/007 FACULDADE Engenharia: Disciplina: Álgebra Linear Professor(a): Data / / Aluno(a): Turma a Lista de Exercícios A álgebra de vetores e a álgebra de matrizes são similares em
Última atualização 16/09/007 FACULDADE Engenharia: Disciplina: Álgebra Linear Professor(a): Data / / Aluno(a): Turma a Lista de Exercícios A álgebra de vetores e a álgebra de matrizes são similares em
INSTITUTO DE MATEMÁTICA E ESTATÍSTICA UNIVERSIDADE DE SÃO PAULO
 EXERCÍCIOS INSTITUTO DE MATEMÁTICA E ESTATÍSTICA UNIVERSIDADE DE SÃO PAULO MAT-2458 Álgebra Linear para Engenharia II Primeira Lista de Exercícios - Professor: Equipe da Disciplina 1. Em R 3, sejam S 1
EXERCÍCIOS INSTITUTO DE MATEMÁTICA E ESTATÍSTICA UNIVERSIDADE DE SÃO PAULO MAT-2458 Álgebra Linear para Engenharia II Primeira Lista de Exercícios - Professor: Equipe da Disciplina 1. Em R 3, sejam S 1
Espaços Vetoriais e Produto Interno
 Universidade Federal do Vale do São Francisco Engenharia Civil Álgebra Linear Prof o. Edson 1 o Semestre 1 a Lista de Exercícios 2009 Data: Sexta-feira 27 de Fevereiro Prof o. Edson Espaços Vetoriais e
Universidade Federal do Vale do São Francisco Engenharia Civil Álgebra Linear Prof o. Edson 1 o Semestre 1 a Lista de Exercícios 2009 Data: Sexta-feira 27 de Fevereiro Prof o. Edson Espaços Vetoriais e
Primeira Lista de Álgebra Linear
 Serviço Público Federal Ministério da Educação Universidade Federal Rural do Semi-Árido UFERSA Departamento de Ciências Ambientais DCA Prof. D. Sc. Antonio Ronaldo Gomes Garcia a a Mossoró-RN 18 de agosto
Serviço Público Federal Ministério da Educação Universidade Federal Rural do Semi-Árido UFERSA Departamento de Ciências Ambientais DCA Prof. D. Sc. Antonio Ronaldo Gomes Garcia a a Mossoró-RN 18 de agosto
Espaços Vetoriais. () Espaços Vetoriais 1 / 17
 Espaços Vetoriais () Espaços Vetoriais 1 / 17 Espaços Vetoriais Definição Seja um conjunto V, não vazio. i. Uma adição em V é uma operação que a cada par de elementos (u, v) V V associa um elemento u +
Espaços Vetoriais () Espaços Vetoriais 1 / 17 Espaços Vetoriais Definição Seja um conjunto V, não vazio. i. Uma adição em V é uma operação que a cada par de elementos (u, v) V V associa um elemento u +
Universidade Federal Fluminense - GAN
 Solimá Gomes Pimentel Universidade Federal Fluminense IM - GAN Solimá Gomes Pimentel, ****- Matemática para Economia III/Solimá Gomes Pimentel 2pt, ; 31cm Inclui Bibliografia. 1. Matemática para Economia
Solimá Gomes Pimentel Universidade Federal Fluminense IM - GAN Solimá Gomes Pimentel, ****- Matemática para Economia III/Solimá Gomes Pimentel 2pt, ; 31cm Inclui Bibliografia. 1. Matemática para Economia
Resolução da 1ª Prova de Álgebra Linear II da UFRJ, período
 www.engenhariafacil.net Resolução da 1ª Prova de Álgebra Linear II da UFRJ, período 2013.1 OBS: Todas as alternativas corretas são as letras A. 1) Para ter ao menos uma solução devemos escalonar para ver
www.engenhariafacil.net Resolução da 1ª Prova de Álgebra Linear II da UFRJ, período 2013.1 OBS: Todas as alternativas corretas são as letras A. 1) Para ter ao menos uma solução devemos escalonar para ver
Lista de exercícios cap. 2
 Lista de exercícios cap. 2 Nos problemas de 1 a 7 apresenta-se um conjunto com as operações de adição e multiplicação por escalar nele definidas. Verificar quais deles são espaços vetoriais. Para aqueles
Lista de exercícios cap. 2 Nos problemas de 1 a 7 apresenta-se um conjunto com as operações de adição e multiplicação por escalar nele definidas. Verificar quais deles são espaços vetoriais. Para aqueles
Álgebra Linear. Professor Alessandro Monteiro. 1º Sábado - Matrizes - 11/03/2017
 º Sábado - Matrizes - //7. Plano e Programa de Ensino. Definição de Matrizes. Exemplos. Definição de Ordem de Uma Matriz. Exemplos. Representação Matriz Genérica m x n 8. Matriz Linha 9. Exemplos. Matriz
º Sábado - Matrizes - //7. Plano e Programa de Ensino. Definição de Matrizes. Exemplos. Definição de Ordem de Uma Matriz. Exemplos. Representação Matriz Genérica m x n 8. Matriz Linha 9. Exemplos. Matriz
Legenda. Questões. 1ª Lista de Exercícios (ALI0001) Prof. Helder G. G. de Lima 1. Cálculos Conceitos Teoria Software
 ª Lista de Exercícios (ALI) Prof. Helder G. G. de Lima Legenda Cálculos Conceitos Teoria Software Questões. Exiba matrizes quadradas A e B de ordem que exemplifiquem as situações a seguir. Compare com
ª Lista de Exercícios (ALI) Prof. Helder G. G. de Lima Legenda Cálculos Conceitos Teoria Software Questões. Exiba matrizes quadradas A e B de ordem que exemplifiquem as situações a seguir. Compare com
5. Seja A uma matriz qualquer. Assinale a afirmativa
 UFRJ Instituto de Matemática Disciplina: Algebra Linear II - MAE 125 Professor: Bruno, Gregório, Luiz Carlos, Mario, Milton, Monique e Umberto Data: 12 de julho de 2013 Terceira Prova 1. Considere no espaço
UFRJ Instituto de Matemática Disciplina: Algebra Linear II - MAE 125 Professor: Bruno, Gregório, Luiz Carlos, Mario, Milton, Monique e Umberto Data: 12 de julho de 2013 Terceira Prova 1. Considere no espaço
Álgebra Linear I. Resumo e Exercícios P3
 Álgebra Linear I Resumo e Exercícios P3 Fórmulas e Resuminho Teórico Espaço Vetorial Qualquer conjunto V com 2 operações: Soma e Produto escalar, tal que 1. u + v + w = u + v + w u, v, w V 2. u + v = v
Álgebra Linear I Resumo e Exercícios P3 Fórmulas e Resuminho Teórico Espaço Vetorial Qualquer conjunto V com 2 operações: Soma e Produto escalar, tal que 1. u + v + w = u + v + w u, v, w V 2. u + v = v
Legenda. Questões. 1ª Lista de Exercícios (ALGA001) Prof. Helder G. G. de Lima 1. Cálculos Conceitos Teoria Software
 ª Lista de Exercícios (ALGA) Prof. Helder G. G. de Lima Legenda Cálculos Conceitos Teoria Software Questões. Mostre que as afirmações a seguir não são necessariamente verdadeiras para matrizes quadradas
ª Lista de Exercícios (ALGA) Prof. Helder G. G. de Lima Legenda Cálculos Conceitos Teoria Software Questões. Mostre que as afirmações a seguir não são necessariamente verdadeiras para matrizes quadradas
ESPAÇOS LINEARES (ou vetoriais)
 Álgebra Linear- 1 o Semestre 2018/19 Cursos: LEIC A Lista 3 (Espaços Lineares) ESPAÇOS LINEARES (ou vetoriais) Notações: Seja A uma matriz e S um conjunto de vetores Núcleo de A: N(A) Espaço das colunas
Álgebra Linear- 1 o Semestre 2018/19 Cursos: LEIC A Lista 3 (Espaços Lineares) ESPAÇOS LINEARES (ou vetoriais) Notações: Seja A uma matriz e S um conjunto de vetores Núcleo de A: N(A) Espaço das colunas
3 a Lista de Exercícios de Introdução à Álgebra Linear IMPA - Verão e B =
 3 a Lista de Exercícios de Introdução à Álgebra Linear IMPA - Verão 2008. (a) Ache os auto-valores e auto-vetores de A = 3 4 2 0 2 0 0 0 e B = 0 0 2 0 2 0 2 0 0 (b) Mostre que λ + λ 2 + λ 3 é igual ao
3 a Lista de Exercícios de Introdução à Álgebra Linear IMPA - Verão 2008. (a) Ache os auto-valores e auto-vetores de A = 3 4 2 0 2 0 0 0 e B = 0 0 2 0 2 0 2 0 0 (b) Mostre que λ + λ 2 + λ 3 é igual ao
Lista de Exercícios 05 Álgebra Matricial
 Lista de Exercícios 05 Álgebra Matricial - 016.1 1. Determine a quantidade desconhecida em cada uma das expressões: ( ) ( ) ( ) T 0 3 x + y + 3 3 w (a) 3.X = (b) = 6 9 4 0 6 z. Uma rede de postos de combustíveis
Lista de Exercícios 05 Álgebra Matricial - 016.1 1. Determine a quantidade desconhecida em cada uma das expressões: ( ) ( ) ( ) T 0 3 x + y + 3 3 w (a) 3.X = (b) = 6 9 4 0 6 z. Uma rede de postos de combustíveis
Espaços Vectoriais. Espaços Vectoriais
 Espaços Vectoriais Espaço vectorial sobre um corpo V - conjunto não vazio de objectos, chamados vectores F - conjunto de escalares, com estrutura de corpo Em V definimos duas operações: - adição de elementos
Espaços Vectoriais Espaço vectorial sobre um corpo V - conjunto não vazio de objectos, chamados vectores F - conjunto de escalares, com estrutura de corpo Em V definimos duas operações: - adição de elementos
Curso de Álgebra Linear
 Curso de Álgebra Linear Fundamentos e Aplicações Terceira Edição 25 de Outubro de 2012 Marco Cabral PhD Indiana University, EUA Paulo Goldfeld PhD Courant Institute, EUA Departamento de Matemática Aplicada
Curso de Álgebra Linear Fundamentos e Aplicações Terceira Edição 25 de Outubro de 2012 Marco Cabral PhD Indiana University, EUA Paulo Goldfeld PhD Courant Institute, EUA Departamento de Matemática Aplicada
Dependência linear e bases
 Dependência linear e bases Sadao Massago 2014 Sumário 1 Dependência linear 1 2 ases e coordenadas 3 3 Matriz mudança de base 5 Neste texto, introduziremos o que é uma base do plano ou do espaço 1 Dependência
Dependência linear e bases Sadao Massago 2014 Sumário 1 Dependência linear 1 2 ases e coordenadas 3 3 Matriz mudança de base 5 Neste texto, introduziremos o que é uma base do plano ou do espaço 1 Dependência
1 Subespaços Associados a uma Matriz
 1 Subespaços Associados a uma Matriz Seja V = R n e para quaisquer u, v, e w em V e quaisquer escalares r,s em R 1, 1. u + v é um elemento de V sempre que u e v são elementos de V a adição é fechada, 2.
1 Subespaços Associados a uma Matriz Seja V = R n e para quaisquer u, v, e w em V e quaisquer escalares r,s em R 1, 1. u + v é um elemento de V sempre que u e v são elementos de V a adição é fechada, 2.
Álgebra Linear. Professor Alessandro Monteiro. 1º Sábado - Matrizes - 11/03/2017
 º Sábado - Matrizes - //7 Plano e Programa de Ensino Matrizes Exemplos Ordem de Uma Matriz Exemplos Representação 7 Matriz Genérica m x n 8 Matriz Linha 9 Exemplos Matriz Coluna Exemplos Diagonal de Uma
º Sábado - Matrizes - //7 Plano e Programa de Ensino Matrizes Exemplos Ordem de Uma Matriz Exemplos Representação 7 Matriz Genérica m x n 8 Matriz Linha 9 Exemplos Matriz Coluna Exemplos Diagonal de Uma
(c) apenas as afirmações (II) e (III) são necessariamente verdadeiras;
 Q1. Considere o espaço vetorial R 4 munido do seu produto interno usual. Sejam B uma base de R 4, A M 4 (R) uma matriz e T : R 4 R 4 a transformação linear tal que [T ] B = A. Considere as seguintes afirmações:
Q1. Considere o espaço vetorial R 4 munido do seu produto interno usual. Sejam B uma base de R 4, A M 4 (R) uma matriz e T : R 4 R 4 a transformação linear tal que [T ] B = A. Considere as seguintes afirmações:
ÁLGEBRA LINEAR I - MAT0032
 UNIVERSIDADE FEDERAL DA INTEGRAÇÃO LATINO-AMERICANA Instituto Latino-Americano de Ciências da Vida e Da Natureza Centro Interdisciplinar de Ciências da Natureza ÁLGEBRA LINEAR I - MAT0032 11 a Lista de
UNIVERSIDADE FEDERAL DA INTEGRAÇÃO LATINO-AMERICANA Instituto Latino-Americano de Ciências da Vida e Da Natureza Centro Interdisciplinar de Ciências da Natureza ÁLGEBRA LINEAR I - MAT0032 11 a Lista de
7. Sejam U, W subespaços vetoriais de um espaço vetorial V sobre um corpo K. Prove que U W é um subespaço vetorial de V se e somente se U W ou W U.
 Lista de Álgebra Linear - Prof. Edson Iwaki 1. Quais dos subconjuntos são R subespaços vetoriais? Ache uma base para os que forem. (a) S = {(x, y, z) R 3 x 0} R 3 (b) S = {(x, y, z) R 3 x = 0} R 3 (c)
Lista de Álgebra Linear - Prof. Edson Iwaki 1. Quais dos subconjuntos são R subespaços vetoriais? Ache uma base para os que forem. (a) S = {(x, y, z) R 3 x 0} R 3 (b) S = {(x, y, z) R 3 x = 0} R 3 (c)
LISTA DE EXERCÍCIOS 1 - MATEMÁTICA 3 (CCM0213)
 LISTA DE EXERCÍCIOS - MATEMÁTICA 3 (CCM3) PROF: PEDRO T. P. LOPES WWW.IME.USP.BR/ PPLOPES/MATEMATICA3 Os exercícios a seguir foram selecionados do livro do Apostol e do Domingues Callioli Costa. Exercício.
LISTA DE EXERCÍCIOS - MATEMÁTICA 3 (CCM3) PROF: PEDRO T. P. LOPES WWW.IME.USP.BR/ PPLOPES/MATEMATICA3 Os exercícios a seguir foram selecionados do livro do Apostol e do Domingues Callioli Costa. Exercício.
(a) (1,5) Obtenha os autovalores e autovetores de L. (b) (1,0) A matriz de L em relação à base canônica de M 2 2 é diagonalizável? Explique.
 Nome do(a) estudante(a): ALI0001(PRO11-0A) Prova IV 8/06/016 Prof. Helder G. G. de Lima ˆ Identifique-se em todas as folhas. ˆ Mantenha o celular e os demais equipamentos eletrônicos desligados durante
Nome do(a) estudante(a): ALI0001(PRO11-0A) Prova IV 8/06/016 Prof. Helder G. G. de Lima ˆ Identifique-se em todas as folhas. ˆ Mantenha o celular e os demais equipamentos eletrônicos desligados durante
Questões. 2ª Lista de Exercícios (Geometria Analítica e Álgebra Linear) Prof. Helder G. G. de Lima 1
 ª Lista de Exercícios (Geometria Analítica e Álgebra Linear) Prof. Helder G. G. de Lima 1 Questões 1. Sejam A, B, C e D vértices de um quadrado. Quantos vetores diferentes entre si podem ser definidos
ª Lista de Exercícios (Geometria Analítica e Álgebra Linear) Prof. Helder G. G. de Lima 1 Questões 1. Sejam A, B, C e D vértices de um quadrado. Quantos vetores diferentes entre si podem ser definidos
ficha 1 matrizes e sistemas de equações lineares
 Exercícios de Álgebra Linear ficha matrizes e sistemas de equações lineares Exercícios coligidos por Jorge Almeida e Lina Oliveira Departamento de Matemática, Instituto Superior Técnico 2 o semestre 2/2
Exercícios de Álgebra Linear ficha matrizes e sistemas de equações lineares Exercícios coligidos por Jorge Almeida e Lina Oliveira Departamento de Matemática, Instituto Superior Técnico 2 o semestre 2/2
ÁLGEBRA LINEAR. Combinação Linear, Subespaços Gerados, Dependência e Independência Linear. Prof. Susie C. Keller
 ÁLGEBRA LINEAR Combinação Linear, Subespaços Gerados, Dependência e Prof. Susie C. Keller Combinação Linear Sejam os vetores v 1, v 2,..., v n do espaço vetorial V e os escalares a 1, a 2,..., a n. Qualquer
ÁLGEBRA LINEAR Combinação Linear, Subespaços Gerados, Dependência e Prof. Susie C. Keller Combinação Linear Sejam os vetores v 1, v 2,..., v n do espaço vetorial V e os escalares a 1, a 2,..., a n. Qualquer
