Aula 6 Produto interno - Aplicações
|
|
|
- Rayssa Van Der Vinne Franco
- 5 Há anos
- Visualizações:
Transcrição
1 Aula 6 Produto interno - Aplicações (continuação) MÓDULO 1 - AULA 6 Objetivos Calcular a distância de um ponto a um círculo e de uma reta a um círculo. Determinar retas tangentes a um círculo. Entender a posição relativa entre dois círculos e calcular a distância entre eles. Nesta aula, continuamos a aplicar as técnicas para determinar distâncias, obtidas através do produto interno, para analisar a posição relativa de pontos, retas e círculos com respeito a círculos. Além disso, veremos como determinar as tangentes a um círculo que passam por um ponto dado. Para isso, apresentamos as noções básicas sobre o círculo no plano incluíndo: a determinação da sua equação; a introdução dos conceitos de retas tangente e normal num ponto pertencente ao círculo; o esboço do gráfico do círculo a partir da sua equação e a identificação de pontos interiores e exteriores a um círculo dado. Preliminares sobre círculos Sejam C um ponto no plano e r um número real positivo. O círculo Γ de centro C e raio r > 0 é o lugar geométrico dos pontos do plano cuja distância ao ponto C é igual a r: Γ = {P d(p, C) = r} Figura 6.1: Círculo de centro C e Determinemos a equação que caracteriza raioos r. pontos do círculo Γ de centro C e raio r > 0. Seja P = (x, y) um ponto de Γ, representado pelas suas coordenadas em relação a um sistema de coordenadas cartesianas fixado. Então, se C = (h, k), temos Sobre círculos... O conteúdo preliminar que apresentamos sobre círculos foi extraído de Pré-Cálculo: Módulo 2, Curvas Planas de J. Delgado Gómez e M. L. Torres Villela, Ed. CECIERJ/CEDERJ. O símbolo Γ é a maiúscula da letra grega γ, que se lê gama. Note que... os dois pontos do círculo Γ, situados sobre uma reta passando pelo centro C, estão a uma distância 2r. Estes pontos são ditos diametralmente opostos. O diâmetro do círculo é o valor 2r. P Γ d(p, C) = r (x h) 2 + (y k) 2 = r. Portanto, o círculo Γ de centro C = (h, k) e raio r, tem equação Γ : (x h) 2 + (y k) 2 = r 2 79 CEDERJ
2 Essa equação se escreve, desenvolvendo os quadrados, na forma x 2 + y 2 2hx 2ky + (h 2 + k 2 r 2 ) = 0, ou seja, a equação do círculo Γ se escreve na chamada forma normal: A equação do círculo Γ ao lado é sua equação canônica. Γ : x 2 + y 2 + Cx + Dy + F = 0 onde C = 2h, D = 2k e F = h 2 + k 2 r 2. No entanto, como veremos mais adiante, nem toda equação que tem essa forma representa um círculo no plano. O gráfico do círculo Γ é o conjunto Graf(Γ) = {(x, y) (x h) 2 + (y k) 2 = r 2 } Exemplo 6.1 A equação do círculo de centro C = (0, 0) e raio r é x 2 + y 2 = r 2. Observe que os pontos (r, 0), ( r, 0), (0, r) e (0, r) são pontos deste círculo. A figura 14.2 ilustra o gráfico deste círculo. Figura 6.2: Círculo de centro (0, 0) e raio r. Exemplo 6.1 Exemplo 6.2 A equação (x+3) 2 +(y 2) 2 = 5 representa um círculo de centro C = ( 3, 2) e raio r = 5. Exemplo 6.3 A equação x 2 + y 2 + 4x 2y 11 = 0 é de um círculo. De fato, reescrevemos esta equação como: A primeira equivalência = foi obtida completando os quadrados dos polinômios nas variáveis x e y. (x 2 + 4x) + (y 2 2y) 11 = 0 (x 2 + 4x + 4 4) + (y 2 2y + 1 1) 11 = 0 ((x + 2) 2 4) + ((y 1) 2 1) 11 = 0 (x + 2) 2 + (y 1) 2 = 16 (x ( 2)) 2 + (y 1) 2 = 4 2. Portanto, o centro do círculo é C = ( 2, 1) e o raio é r = 4. CEDERJ 80
3 MÓDULO 1 - AULA 6 Exemplo 6.4 Que subconjuntos do plano representam as equações x 2 + y 2 + 4x 2y + 5 = 0 e x 2 + y 2 + 4x 2y + 6 = 0? Veremos que estes conjuntos não são círculos. De fato, as duas equações diferem da equação do exemplo anterior apenas no termo independente de x e y, isto é, a constante. Procedendo de maneira análoga ao exemplo anterior, completamos os quadrados nas duas equações, olhando para os polinômios nas variáveis x e y: (x 2 + 4x) + (y 2 2y) + 5 = 0 (x 2 + 4x + 4 4) + (y 2 2y + 1 1) + 5 = 0 ((x + 2) 2 4) + ((y 1) 2 1) + 5 = 0 (x + 2) 2 + (y 1) 2 = 0, e (x 2 + 4x) + (y 2 2y) + 6 = 0 (x 2 + 4x + 4 4) + (y 2 2y + 1 1) + 6 = 0 ((x + 2) 2 4) + ((y 1) 2 1) + 6 = 0 (x + 2) 2 + (y 1) 2 = 1. Como a soma de quadrados de números reais é sempre um número real maior ou igual a zero, temos que a única solução da primeira equação é x + 2 = 0 e y 1 = 0. Entretanto, não há solução, em pares de números reais, para a segunda equação. Logo, apenas o ponto ( 2, 1) é solução da primeira equação e não há solução em pares (x, y) de números reais, para a segunda equação, isto é, o conjunto solução da segunda equação é o conjunto vazio. Cuidado! Como acabamos de verificar, a equação x 2 + y 2 + ax + by + c = 0 nem sempre representa um círculo, ela pode representar um único ponto ou o conjunto vazio. 81 CEDERJ
4 Para determinar o subconjunto do plano que esta equação representa, completamos os quadrados, repetindo o que foi feito no exemplo anterior: x 2 + y 2 + ax + by + c = 0 ( ) ( ) x 2 + ax + a2 4 a2 + y 2 + by + b2 4 4 b2 + c = 0 4 ( x + a ) ( 2 + y + b ) 2 a b2 4 + c = 0 ( x + a ) ( 2 + y + b ) 2 = a b2 4 c ( x + a ) ( 2 + y + b ) 2 = a2 + b 2 4c Agora, podemos responder à pergunta. Qual o subconjunto do plano Γ = { (x, y) x 2 + y 2 + ax + by + c = 0 }? ( o ponto P = a 2, b ), se a 2 + b 2 4c = 0 2 Γ = o círculo de centro C e raio r, se a 2 + b 2 4c > 0 o conjunto vazio, se a 2 + b 2 4c < 0. No segundo caso, o círculo Γ tem: ( centro C = a 2, b ) a2 + b e raio r = 2 4c. 2 2 Em cada ponto P de um círculo, considere a reta n que passa pelo centro C e pelo ponto P. Esta reta é dita normal ao círculo no ponto P. A reta t que passa pelo ponto P e é perpendicular à reta n é chamada tangente ao círculo no ponto P. Figura 6.3: Tangente e normal ao círculo Exemplo 6.5 em P. Determinemos as equações das retas horizontais e tangentes ao círculo de centro C = ( 2, 2) e raio r = 3. A equação deste círculo é (x ( 2)) 2 + (y 2) 2 = 9, isto é (x + 2) 2 + (y 2) 2 = 9. CEDERJ 82
5 MÓDULO 1 - AULA 6 As retas tangentes horizontais são perpendiculares à reta vertical s que passa pelo centro C = ( 2, 2). A equação da reta s é x = 2. Para determinar a interseção do círculo com a reta s, substituímos a equação de s na equação do círculo, ou seja, fazemos x = 2 na equação do círculo: ( 2 + 2) 2 + (y 2) 2 = 9 (y 2) 2 = 9, extraindo a raiz quadrada, y 2 = 3 y 2 = 3 ou y 2 = 3 y = 5 ou y = 1. Portanto, os pontos do círculo que estão na reta s são ( 2, 5) e ( 2, 1). As retas tangentes ao círculo passando por estes pontos são horizontais e têm equações y = 5 e y = 1. Exemplo 6.6 Fixemos o círculo Γ de centro C = (1, 2) e raio 3, cuja equação é (x 1) 2 + (y 2) 2 = 9. Os pontos P = (a, b) tais que (a 1) 2 + (b 2) 2 9 não estão no círculo Γ. Por exemplo, os pontos A = ( 1, 3) e B = (2, 5) têm esta propriedade, pois: 5, se (a, b) = ( 1, 3) (a 1) 2 + (b 2) 2 = 10, se (a, b) = (2, 5). Faça um desenho de Γ e observe que A está na região do plano limitada por Γ e que B está na região do plano exterior ao círculo Γ (região ilimitada). Os pontos P = (a, b) tais que (a 1) 2 + (b 2) 2 < 9 são ditos pontos interiores ao círculo Γ. Por outro lado, os pontos P = (a, b) tais que (a 1) 2 + (b 2) 2 > 9 são ditos pontos exteriores ao círculo Γ. Em geral, se a equação de um círculo é (x h) 2 + (y k) 2 = r 2 e P = (x 0, y 0 ) é um ponto do plano, então P está no interior do círculo (x 0 h) 2 + (y 0 k) 2 < r 2. P está no círculo (x 0 h) 2 + (y 0 k) 2 = r 2. P está no exterior do círculo (x 0 h) 2 + (y 0 k) 2 > r CEDERJ
6 Exemplo 6.7 Na figura ao lado, esboçamos o gráfico do círculo de centro C = ( 2, 1) e raio r = 5, cuja equação é 2 (x + 2) 2 + (y 1) 2 = O ponto A = ( 2, 3) está no interior do círculo e o ponto B = (1, 2) está no exterior do círculo. Dê outros exemplos de pontos situados no interior e exterior deste círculo. Figura 6.4: Círculo de centro ( 2, 1) e raio 5 2. Resumindo: O círculo Γ de centro no ponto P 0 e raio r divide o plano em três subconjuntos disjuntos (Figura 6.5): O conjunto dos pontos de Γ. O conjunto de pontos interiores a Γ (ou abreviadamente, o interior de Γ) que consiste dos pontos P do plano, tais que d(p, P 0 ) < r. O conjunto de pontos exteriores a Γ (ou simplesmente, o exterior de Γ) que consiste dos pontos P do plano, tais que d(p, P 0 ) > r. Figura 6.5: P 1 é ponto interior a Γ; P 2 é ponto exterior a Γ; P 3 Γ. Distância de um ponto a um círculo. A distância de um ponto P do plano ao círculo Γ, que designamos por d(p, Γ) é por definição a menor das distâncias de P aos pontos de Γ. Assim, se P Γ, então d(p, Γ) = 0 e, se P = P 0, então d(p, Γ) = r. Se P é um ponto do plano que não pertence a Γ e é diferente do centro P 0, então a semi-reta com origem em P 0 que passa por P intersecta o círculo Γ num único ponto Q. Usando congruência de triângulos, mostraremos que d(p, Γ) = d(p, Q). CEDERJ 84
7 MÓDULO 1 - AULA 6 Para isso, devemos verificar que qualquer outro ponto Q de Γ distinto de Q, satisfaz P Q > P Q. Suponhamos que P seja um ponto interior a Γ distinto do centro. Então, o triângulo P 0 QQ é isósceles e portanto P 0 QQ = P 0 Q Q Figura 6.6: P é interior a Γ. (Figura 6.6). Além disso, no triângulo P QQ, temos: P Q Q < P 0 Q Q = P 0 QQ = P QQ. Logo, o ângulo oposto a P Q é menor que o ângulo oposto a P Q. Portanto P Q < P Q. Suponhamos agora que P seja um ponto exterior a Γ. Como o triângulo P 0 QQ é isósceles (Figura 6.7), P 0 QQ é um ângulo agudo. Logo, P QQ é um ângulo obtuso e, portanto, P Q Q é um ângulo agudo. Assim, o ângulo oposto a P Q é menor Figura 6.7: P é exterior a Γ. que o ângulo oposto a P Q e, portanto, P Q < P Q. Desta maneira, vemos que para determinar d(p, Γ), sendo P P 0, basta determinar d(p, Q) = P Q. Isto é feito da seguinte maneira: Se P é um ponto interior a Γ (Figura 6.6): d(p, Γ) = r d(p, P 0 ) = r P 0 P. Se P é um ponto de Γ, então d(p, Γ) = 0. Se P é um ponto exterior a Γ (Figura 6.7): d(p, Γ) = d(p, P 0 ) r = P 0 P r. Assim, qualquer que seja a posição relativa de P com respeito a Γ, temos: d(p, Γ) = r d(p 0, P ) = r P 0 P (6.1) Exemplo 6.8 Seja Γ o círculo de equação (x 3) 2 + (y + 1) 2 = 4. Determinemos a posição relativa dos pontos P 1 = (1, 1), P 2 = (3, 3) e P 3 = (2, 0) com respeito ao círculo Γ e calculemos as suas distâncias a Γ. Veja a Figura CEDERJ
8 Figura 6.8: 6.8. Exemplo Sobre a figura 6.9 Para mostrar que d(q, s) < d(q, s), observe que, no quadrilátero QP P Q, os ângulos QP P e P P Q são retos, enquanto Q QP é obtuso, pois o triângulo QQ P 0 é isósceles (verifique!). Isso implica que QP P Q não é um paralelogramo e que Solução: O círculo Γ tem o seu centro no ponto P 0 = (3, 1) e raio r = 2. Para determinar a posição relativa dos pontos com respeito a Γ, devemos calcular a sua distância ao centro P 0 : a. d(p 0, P 1 ) = P 0 P 1 = (1 3) 2 + (1 ( 1)) 2 = = 8 = 2 2 > 2 = r, logo P 1 é um ponto exterior a Γ. Usando a equação (6.1): d(p 1, Γ) = 2 P 0 P 1 = = 2( 2 1). b. d(p 0, P 2 ) = P 0 P 2 = (3 3) 2 + ( 3 ( 1)) 2 = = 2 = r, logo P 2 é um ponto de Γ. Portanto d(p 2, Γ) = 0. c. d(p 0, P 3 ) = P 0 P 3 = (2 3) 2 + (0 ( 1)) 2 = = 2 < 2 = r, logo P 3 é um ponto interior a Γ. Usando a equação (6.1), temos: d(p 3, Γ) = 2 P 0 P 3 = 2 2 = 2 2. Distância de uma reta a um círculo. Seja Γ o círculo de centro P 0 e raio r. Sabemos que uma reta s pode ou não intersectar o círculo Γ. A distância da reta s ao círculo Γ, que designamos por d(s, Γ), é definida como sendo a menor das distâncias dos pontos de Γ à reta s. QP < Q P. Assim, se s Γ, então d(s, Γ) = 0. Figura 6.9: d(s, Γ) = d(p, Q) = d(p 0, s) r. Para verificar se s e Γ se intersectam ou não, basta determinar a distância do centro P 0 do círculo à reta s: Se d(p 0, s) r, então s Γ. Se d(p 0, s) > r, então s Γ =. Usando seus conhecimentos de Geometria Elementar, você pode verificar que, se s Γ = e Q é o ponto onde a reta perpendicular a s que passa por P 0 intersecta Γ, então a distância de s a Γ é a distância de Q a s. Isto é, se Q é outro ponto qualquer de Γ, diferente de Q, então d(q, s) > d(q, s) (veja a Figura 6.9). maneira: Na prática, se s Γ =, a distância de s a Γ é obtida da seguinte Calculamos a distância do centro P 0 à reta s (que você já sabe como calcular) e subtraímos a medida do raio (Figura 6.9). Ou seja, s Γ = = d(s, Γ) = d(p 0, s) r CEDERJ 86
9 MÓDULO 1 - AULA 6 Portanto, se a reta s tem equação cartesiana ax + by = c e P 0 = (x 0, y 0 ), obtemos: d(s, Γ) = d(p 0, s) r = ax 0 + by 0 c a 2 + b 2 r Exemplo 6.9 Sejam s reta de equação cartesiana 3x 4y = 7 e Γ o círculo de equação x 2 + y 2 3x + 2 = 0. Calculemos d(s, Γ). Solução: Primeiro precisamos obter as coordenadas do centro P 0 e o raio r do círculo Γ. Para tanto, devemos escrever a equação de Γ na forma canônica: (x x 0 ) 2 + (y y 0 ) 2 = r 2. Vejamos: x 2 + y 2 3x + 2 = 0 = x 2 3x y2 9 ( = 0 = x y 2) 2 = 1 4. Figura 6.10: Exemplo 6.9. Assim, Γ é o círculo de centro P 0 = ( 3 2, 0) e raio r = 1 2. Logo, d(p 0, s) = 4(0) ( 7) = ( 4) = Portanto, a distância de s a Γ (em unidades de comprimento) é: d(r, Γ) = d(p 0, s) r = = = 9 5. De volta às retas tangentes a um círculo. Sabemos que a equação canônica do círculo Γ de centro P 0 e raio r é (x x 0 ) 2 + (y y 0 ) 2 = r 2. Seja P = (x 1, y 1 ) um ponto exterior a Γ. Lembre que... Uma reta r é tangente ao círculo Γ, se r Γ consiste de um único ponto, denominado ponto de tangência. A propriedade fundamental de uma reta tangente a um círculo é que ela é perpendicular à reta que passa pelo centro do círculo e pelo ponto de tangência (reta normal a Γ). 87 CEDERJ
10 Determinemos as equações das retas tangentes a Γ passando pelo ponto P. Na Figura 6.11 vemos que sempre é possível traçar duas retas tangentes a Γ passando pelo ponto P. Para determinar essas retas, precisamos determinar os pontos Q e Q onde elas são tangentes ao círculo Γ. Uma reta r passando por P é tangente ao círculo Γ no ponto Q Γ se, e somente se, Figura 6.11: Tangentes a Γ. Q r e r é perpendicular à reta que passa por Q e pelo centro P 0 de Γ. Isto é, os vetores diretores P Q e P 0 Q dessas retas, devem ser perpendiculares: P Q, P 0 Q = 0. Observando que P Q = P P 0 + P 0 Q (veja a Figura 6.11), a identidade anterior se escreve: 0 = P P 0 + P 0 Q, P 0 Q = P P 0, P 0 Q + P 0 Q, P 0 Q. Como Q Γ, temos P 0 Q, P 0 Q = P 0 Q 2 = d(q, P 0 ) 2 = r 2. Logo: r 2 + P P 0, P 0 Q = 0, e sendo que P P 0 = P 0 P, obtemos: P 0 P, P 0 Q = r 2. Substituindo nessa identidade as coordenadas P 0 = (x 0, y 0 ), P = (x 1, y 1 ) e Q = (x, y), obtemos: (x x 0 )(x 1 x 0 ) + (y y 0 )(y 1 y 0 ) = r 2. Além disso, como o ponto Q pertence ao círculo Γ, as coordenadas (x, y) de Q devem satisfazer também a equação de Γ: (x x 0 ) 2 + (y y 0 ) 2 = r 2. Assim, para determinarmos as coordenadas do ponto Q = (x, y) devemos resolver o sistema formado pelas duas equações: (x x 0 )(x 1 x 0 ) + (y y 0 )(y 1 y 0 ) = r 2 (6.2) (x x 0 ) 2 + (y y 0 ) 2 = r 2 Esse sistema possui duas soluções Q = (x, y) e Q = (x, y ). Isso significa que há duas retas tangentes a Γ passando pelo ponto P : a reta r que contém P e Q, e a reta r que contém P e Q (veja a Figura 6.11). CEDERJ 88
11 MÓDULO 1 - AULA 6 Exemplo 6.10 Determinemos as retas tangentes ao círculo Γ : (x 3) 2 + (y 1) 2 = 2 que passam pelo ponto P = (6, 2). Solução: Substituindo as coordenadas do centro P 0 = (x 0, y 0 ) = (3, 1) de Γ e do ponto P = (x 1, y 1 ) = (6, 2) no sistema (6.2), obtemos: (6 3)(x 3) + (2 1)(y 1) = 2 3(x 3) + y 1 = 2, isto é (x 3) 2 + (y 1) 2 = 2 (x 3) 2 + (y 1) 2 = 2. Da primeira equação, temos y 1 = 2 3(x 3) = 3x + 11 e substituindo na segunda equação: (x 3) 2 + ( 3x + 11) 2 = 2 = x 2 6x x 2 66x = 2 = 10x 2 72x = 0 = 5x 2 36x + 64 = 0. As soluções desta última equação são x = 4, e x = 16. Substituindo esses 5 valores na expressão y = 3x + 12, encontramos os respectivos valores de y: x = 4 = y = 3(4) + 12 = 0, logo Q = (4, 0); x = 16 = 5 y = = = 12, logo Q = ( 16, 12). 5 5 Deixamos você verificar que a reta r 1 tangente a Γ que passa por P e Q tem equação r 1 : x y = 4 e que a reta r 2 tangente a Γ que passa por P e Q tem equação (veja a Figura 6.12) r 2 : 7y x = 20. Figura 6.12: Exemplo Além disso, comprove também que a reta que passa pelo ponto P e pelo centro P 0 de Γ é uma bissetriz das retas tangentes r 1 e r 2. Distância entre círculos. A distância e a posição relativa entre dois círculos podem ser analisadas usando outros recursos da Geometria plana. No entanto, é muito importante que você saiba efetuar a análise no contexto do cálculo de distâncias derivado da noção de produto interno. Começamos considerando dois círculos Γ 1 e Γ 2 de centros P 1, P 2 e raios r 1 e r 2, respectivamente. Pode acontecer que Γ 1 Γ 2 = ou que Γ 1 Γ 2. No segundo caso dizemos que a distância entre Γ 1 e Γ 2, que denotamos por d(γ 1, Γ 2 ), é igual a zero. Estudemos o caso em que Γ 1 Γ 2 =. 89 CEDERJ
12 Lembre que... O interior de um círculo Γ de centro P e raio r é o conjunto dos pontos Q do plano, tais que d(p, Q) < r. Analogamente, o exterior de Γ consiste dos pontos Q do plano, tais que d(p, Q) > r. Finalmente, o círculo Γ consiste dos pontos que ficam na fronteira entre o interior e o exterior, isto é, consiste dos pontos Q, tais que d(p, Q) = r. Sejam Ω 1 o interior de Γ 1 e Ω 2 o interior de Γ 2, respectivamente e analisemos, separadamente, as possíveis posições relativas entre Γ 1 e Γ 2 : a. Γ 2 Ω 1 (note que o caso Γ 1 Ω 2 é analisado de maneira similar). b. Ω 1 Ω 2 = (isto é, os interiores de Γ 1 e Γ 2 não têm pontos em comum). Caso a. Γ 2 Ω 1. Neste caso, existem ainda as seguintes possibilidades: Caso a1. Γ 2 Ω 1 e P 1 Γ 2 Ω 2. Consideremos a semi-reta l com origem em P 1 passando por P 2. P 2 Observe que pode acontecer que P 1 = (círculos concêntricos) em cujo caso consideramos uma semi-reta qualquer com origem em P 1. A semi-reta l (mesmo no caso dos Figura 6.13: Γ 2 Ω 1 e P 1 Γ 2 Ω 2. círculos serem concêntricos) intersecta Γ 1 em um único ponto Q 1 e Γ 2 em um ponto Q 2 diferente de P 1. Você pode verificar, usando Geometria Elementar, que Q 2 é o ponto de Γ 2 que está mais próximo de Γ 1. Definimos então a distância de Γ 1 a Γ 2, que designamos por d(γ 1, Γ 2 ) da seguinte maneira: d(γ 1, Γ 2 ) = Q 1 Q 2 = P 1 Q 1 P 1 Q 2 = r 1 P 1 Q 2. Como P 1 Q 2 = P 1 P 2 + P 2 Q 2, temos: d(γ 1, Γ 2 ) = r 1 P 1 Q 2 = r 1 P 1 P 2 P 2 Q 2 = r 1 P 1 P 2 r 2. Logo d(γ 1, Γ 2 ) = r 1 r 2 P 1 P 2, onde r 1 é o raio do círculo maior Γ 1 e r 2 é o raio do círculo menor Γ 2. Como o caso em que Γ 1 Ω 2 e P 2 Ω 1 é analisado de forma análoga, trocando o índice 1 por 2, obtemos d(γ 1, Γ 2 ) = r 2 r 1 P 2 P 1, onde r 2 é o raio do círculo maior e r 1 é o raio do círculo menor. Portanto, se um círculo está contido no interior do outro e o centro do círculo maior está contido no interior ou sobre o círculo menor, temos: CEDERJ 90
13 MÓDULO 1 - AULA 6 d(γ 1, Γ 2 ) = r 2 r 1 P 1 P 2. Com esta fórmula calculamos ainda a distância de Γ 1 a Γ 2 quando os círculos são concêntricos (Figura 6.14), pois, nesse caso, P 1 = P 2 e d(γ 1, Γ 2 ) = r 2 r 1. Caso a2. Γ 2 Ω 1 e P 1 Γ 2 Ω 2. Neste caso, a semi-reta l com origem em P 1 e que passa por P 2, intersecta o círculo Γ 2 em dois pontos Q 2 e Q 2, pertencentes a um diâmetro de Γ 2. Isto é, pontos de Γ 2 que são diametralmente opostos. Figura 6.14: concêntricos. Círculos Escolhemos os nomes dos pontos Q 2 e Q 2 de modo que P 1 Q 2 < P 1 Q 2. Assim, Q 2 é o ponto de Γ 2 que está mais próximo de Γ 1. Logo, a distância de Γ 1 a Γ 2 é: Figura 6.15: Γ 2 Ω 1 e P 1 Γ 2 Ω 2. d(γ 1, Γ 2 ) = Q 1 Q 2 = P 1 Q 1 P 1 Q 2 = P 1 Q 1 ( P 1 P 2 + P 2 Q 2 ). Como obtemos: P 1 Q 1 = r 1, e P 2 Q 2 = r 2, d(γ 1, Γ 2 ) = r 1 P 1 P 2 r 2 = r 1 r 2 P 1 P 2. Analogamente, se Γ 1 Ω 2 e P 2 Ω 1, obtemos d(γ 1, Γ 2 ) = r 2 r 1 P 2 P 1. Resumimos a análise dos casos a1. e a2. da seguinte maneira: Proposição 6.13 Sejam Γ 1 e Γ 2 os círculos de centros P 1 e P 2 e raios r 1 e r 2 respectivamente. Suponhamos que Γ 1 Γ 2 = e que Γ 1 está contido no interior de Γ 2 ou Γ 2 está contido no interior de Γ 1. Então, a distância de Γ 1 a Γ 2 é: d(γ 1, Γ 2 ) = r 2 r 1 P 1 P 2 (6.3) 91 CEDERJ
14 Caso b. Ω 1 Ω 2 =. Consideremos o segmento P 1 P 2 ligando os centros de Γ 1 e Γ 2. Como Γ 1 Γ 2 = e Ω 1 Ω 2 =, o segmento P 1 P 2 intersecta Γ 1 num ponto que designamos Q 1 e também intersecta Γ 2 num ponto que designamos Q 2. Figura 6.16: Γ 1 Γ 2 e Ω 1 Ω 2 =. Usando Geometria Elementar podemos mostrar que o ponto Q 1 é o ponto de Γ 1 que está mais próximo de Γ 2 e que o ponto Q 2 é o ponto de Γ 2 que está mais próximo de Γ 1 e que quaisquer que sejam os pontos Q 1 Γ 1 e Q 2 Γ 2, com Q 1 Q 1 ou Q 2 Q 2, tem-se Q 1Q 2 < Q 1 Q 2 (veja a Figura 6.16). Portanto, d(γ 1, Γ 2 ) = d(q 1, Q 2 ) = Q 1 Q 2. Como Q 1 Q 2 = P 1 P 2 P 1 Q 1 P 2 Q 2 = P 1 P 2 r 1 r 2, obtemos: Proposição 6.14 Sejam Γ 1 e Γ 2 círculos de centros P 1 e P 2, raios r 1 e r 2 e interiores Ω 1 e Ω 2 respectivamente. Suponhamos que Γ 1 Γ 2 = e Ω 1 Ω 2 =. Então: d(γ 1, Γ 2 ) = P 1 P 2 (r 1 + r 2 ) (6.4) Exemplo 6.11 Sejam Γ 1 o círculo de equação (x 1) 2 + (y + 2) 2 = 2 e Γ 2 o círculo de equação (x + 2) 2 + (y 1) 2 = 36. Mostremos que Γ 1 e Γ 2 não se intersectam e calculemos d(γ 1, Γ 2 ). Solução: Para mostrar que Γ 1 e Γ 2 não se intersectam devemos mostrar que o sistema abaixo não tem solução: (x 1) 2 + (y + 2) 2 = 2 (x + 2) 2 + (y 1) 2 = 36. Suponhamos, pelo absurdo, que o sistema tenha solução e procuremos por ela. Uma maneira simples de resolver esse sistema é evitar desenvolver os quadrados imediatamente e reescrever a segunda equação de forma que possamos utilizar melhor a primeira. Observe: CEDERJ 92
15 MÓDULO 1 - AULA 6 (x + 2) 2 + (y 1) 2 = 36 (x 1 }{{} +3)2 + (y + 2 }{{} 3)2 = 36 (x 1) 2 + 6(x 1) (y + 2)2 6(y + 2) + 9 = 36 }{{}}{{} 2 + 6(x 1) + 9 6(y + 2) + 9 = 36 6(x 1) 6(y + 2) = 16 3(x 1) 3(y + 2) = 8 3(x 1) = 3y + 14, 3y + 17 de onde obtemos x em função de y: x =. 3 Substituindo essa expressão obtida para x na primeira equação do sistema, temos: 3y + 17 ( 1) 2 + (y + 2) 2 3y + 14 = 2 = ( ) 2 + (y + 2) 2 = = (3y + 14)2 9 + (y + 2) 2 = 2 = (3y + 14) 2 + 9(y + 2) 2 = 18 = 9y y = 0. Essa equação não tem raízes reais, pois o seu discriminante é: = = 36( ) < 0. Isso mostra que círculos Γ 1 e Γ 2 não se intersectam. Para calcular d(γ 1, Γ 2 ), determinamos a distância entre os centros P 1 = (1, 2) de Γ 1 (cujo raio é r 1 = 2) e P 2 = ( 2, 1) de Γ 2 (cujo raio é r 2 = 6): P 1 P 2 = ( 2 1) 2 + (1 ( 2)) 2 = 18 = 3 2. Como a distância de P 1 a P 2 é menor que a soma dos raios r 1 + r 2 = 6 + 2, estamos na situação do Caso a. Calculamos a distância de Γ 1 a Γ 2, em unidades de comprimento, usando a fórmula (6.3): Figura 6.17: 6.11 Exemplo d(γ 1, Γ 2 ) = r 2 r 1 P 1 P 2 = = CEDERJ
16 Resumo Nesta aula vimos como aplicar a noção de produto interno (via o cálculo de normas), para determinar a distância de um ponto, uma reta ou um círculo a um círculo e as tangentes a um círculo passando por um ponto dado. Exercícios 1. Determine a distância do ponto P ao círculo Γ, onde: a. P = (1, 1), Γ : x 2 + (y 2) 2 = 4. b. P = ( 10, 1), Γ : (x 2) 2 + (y 5) 2 = 9. c. P = (0, 0), Γ : (x + 2) 2 + (y 3) 2 = 4. d. P = ( 1, 1), Γ : x 2 + y 2 = 16. e. P = ( 7, 1), Γ : x 2 + y 2 5y = Calcule a distância da reta r ao círculo Γ, onde: a. r : x 3y = 2, Γ : (x 7) 2 + (y + 1) 2 = 3. b. r : y = 2x 1, Γ : (x + 1) 2 + (y + 2) 2 = 4. x = 3 + 2t c. r :, t R, Γ : (x 7) 2 + (y + 1) 2 = 3. y = 1 5t x = t d. r :, t R,, Γ : x 2 + y 2 14x + 2y = 12. y = 2 3t 3. Dê as equações das retas tangentes ao círculo Γ que passam pelo ponto P, onde: a. Γ : (x 7) 2 + (y + 1) 2 = 3, P = ( 3, 2). b. Γ : x 2 + (y 1) 2 = 4, P = (5, 1). c. Γ : (x 1) 2 + y 2 = 3, P = (6, 0). 4. Calcule a distância entre os círculos Γ 1 e Γ 2, onde: a. Γ 1 : (x 5) 2 + (y 1) 2 = 36 e Γ 2 : (x 3) 2 + (y + 2) 2 = 1. b. Γ 1 : x 2 + (y 1) 2 = 64 e Γ 2 : (x 1) 2 + (y + 1) 2 = 4. CEDERJ 94
17 MÓDULO 1 - AULA 6 c. Γ 1 : (x 1) 2 + (y 1) 2 = 1 e Γ 2 : (x 5) 2 + (y + 3) 2 = 1. d. Γ 1 : (x 3) 2 + (y 3) 2 = 16 e Γ 2 : x 2 + y 2 6(x + y) + 14 = Considere os círculos: Γ 1 : (x 2) 2 + (y 4) 2 = 17 e Γ 2 : (x + 2) 2 + y 2 = 9. a. Verifique que os círculos Γ 1 e Γ 2 se intersectam. b. Calcule a distância entre os pontos de interseção dos círculos Γ 1, Γ 2. c. Determine a distância dos pontos de interseção à reta que passa pelos centros de Γ 1 e Γ Determine a posição relativa dos círculos Γ 1 e Γ 2, onde: a. Γ 1 : (x 1) 2 + (y 3) 2 = 4 e Γ 2 : (x 1) 2 + (y 7) 2 = 4. b. Γ 1 : (x 1) 2 + (y + 3) 2 = 4 e Γ 2 : (x 1) 2 + (y 7) 2 = 4. c. Γ 1 : (x 1) 2 + (y 3) 2 = 4 e Γ 2 : (x + 1) 2 + (y 7) 2 = 4. d. Γ 1 : (x + 1) 2 + (y 3) 2 = 4 e Γ 2 : (x + 1) 2 + (y 7) 2 = 4. Auto-avaliação Os exercícios têm por objetivo fixar as técnicas apresentadas na aula. Você deverá resolvê-los todos e, se tiver ainda alguma dificuldade, reveja o conteúdo da aula ou procure ajuda dos tutores. Não esqueça de trocar idéias com seus colegas. 95 CEDERJ
18
19 Simetrias e simetrias das cônicas MÓDULO 1 - AULA 7 Aula 7 Simetrias e simetrias das cônicas Objetivos Estudar as simetrias em relação a um ponto e em relação a uma reta. Estudar as simetrias das cônicas no plano. Entender as cônicas degeneradas. IMPORTANTE Nas próximas aulas deste Módulo, assumimos os conceitos fundamentais sobre as curvas cônicas, apresentados no Pré-Cálculo, já conhecidos. Lembremos que as curvas cônicas são assim denominadas por serem obtidas pela interseção de um plano com um duplo cone circular reto (Figura 7.1). Nas ilustrações abaixo, mostramos algumas curvas cônicas: o círculo, a elipse, a parábola e a hipérbole: Figura 7.2: Círculo. Figura 7.3: Elipse. Nos seus escritos, o matemático grego Pappus de Alexandria ( ), atribuiu ao geômetra grego Aristeu o Ancião ( a.c.) o crédito de ter publicado o primeiro tratado sobre as seções cônicas, referindo-se aos Cinco livros sobre seções cônicas de Aristeu, nos quais foi apresentado um estudo cuidadoso das curvas cônicas e as suas propriedades. Figura 7.1: Cone circular reto. O duplo cone circular reto é a superfície descrita por uma reta l chamada geratriz, ao girar mantendo um ângulo constante, em torno de outra reta d, chamada diretriz do cone duplo, e com a qual tem um ponto em comum, chamado vértice do cone. Cortando esse cone duplo por planos, obtemos as curvas cônicas. Figura 7.4: Parábola. Figura 7.5: Hipérbole. 97 CEDERJ
20 Simetrias e simetrias das cônicas Para saber mais... Sobre Aristeu o Ancião, veja: st-and.ac.uk/~history/ Mathematicians/Aristaeus. html e sobre Menaecmus, veja: st-andrews.ac.uk/history/ Mathematicians/ Menaechmus.html Apolônio de Perga a.c. Nasceu em Ionia, Grécia (hoje Turquia) e faleceu em Alexandria, Egito, onde passou a maior parte da sua vida. Embora a sua formação fosse em Astronomia, escreveu sobre vários tópicos matemáticos, sendo Seções Cônicas o mais famoso deles. A obra original consistia de oito livros, dos quais apenas sete são conhecidos. Os primeiros quatro chegaram à Europa numa tradução grega e os outros três numa tradução árabe do século IX. Apolônio resumiu nos primeiros três livros, toda a teoria desenvolvida por Aristeu e Euclides, dedicando os cinco livros restantes à pesquisa original sobre as propriedades das seções cônicas. Veja: st-and.ac.uk/~history/ Mathematicians/ Apollonius.html Segundo Pappus, o matemático grego Euclides de Alexandria ( a.c.), contemporâneo de Aristeu, conhecia muito bem os cinco livros sobre as curvas cônicas e evitou aprofundar-se sobre esse assunto na sua obra Os elementos, de modo a obrigar os leitores interessados a consultar a obra original de Aristeu. Duzentos anos mais tarde, o astrônomo e matemático grego Apolônio de Perga ( a.c.) recompilou e aprimorou os resultados de Aristeu e de Euclides nos oito livros da sua obra Seções Cônicas. No entanto, a História indica que as cônicas foram descobertas pelo matemático grego Menaecmus ( a.c. aproximadamente) quando estudava como resolver os três problemas famosos da Geometria grega: a triseção do ângulo, a duplicação do cubo e a quadratura do círculo. Segundo o historiador Proclus, Menaecmus nasceu em Alopeconnesus, na Ásia Menor (o que hoje é a Turquia), foi aluno de Eudóxio na academia de Platão. Menaecmus foi o primeiro em mostrar que as elipses, parábolas e hipérboles são obtidas cortando um cone com um plano não paralelo à sua base. Mesmo assim, pensava-se que os nomes dessas curvas foram inventados por Apolônio, porém traduções de antigos escritos árabes indicam a existência desses nomes em épocas anteriores a Apolônio. Notação. Designaremos por OXY um sistema cartesiano ortogonal de coordenadas de origem O e eixos coordenados OX e OY. As equações canônicas das curvas cônicas no sistema de coordenadas OXY são: x 2 Elipse: a + y2 = 1, com a > 0 e b > 0. Se a = b então a elipse é o 2 b2 círculo de raio a. x 2 Figura 7.6: Elipse. Hipérbole: a y2 y2 = 1 ou 2 b2 a x2 2 b = 1, com a > 0 e b > 0. 2 Parábola: x 2 = ky ou y 2 = kx, com k 0. CEDERJ 98
Aula 7 Simetrias e simetrias das cônicas
 MÓDULO 1 - AULA 7 Aula 7 Simetrias e simetrias das cônicas Objetivos Estudar as simetrias em relação a um ponto e em relação a uma reta. Estudar as simetrias das cônicas no plano. Entender as cônicas degeneradas.
MÓDULO 1 - AULA 7 Aula 7 Simetrias e simetrias das cônicas Objetivos Estudar as simetrias em relação a um ponto e em relação a uma reta. Estudar as simetrias das cônicas no plano. Entender as cônicas degeneradas.
Objetivos. em termos de produtos internos de vetores.
 Aula 5 Produto interno - Aplicações MÓDULO 1 - AULA 5 Objetivos Calcular áreas de paralelogramos e triângulos. Calcular a distância de um ponto a uma reta e entre duas retas. Determinar as bissetrizes
Aula 5 Produto interno - Aplicações MÓDULO 1 - AULA 5 Objetivos Calcular áreas de paralelogramos e triângulos. Calcular a distância de um ponto a uma reta e entre duas retas. Determinar as bissetrizes
Aula 8 Cônicas - Translação de sistemas de coordenadas
 Aula 8 Cônicas - Translação de sistemas de coordenadas MÓDULO 1 - AULA 8 Objetivos Entender a mudança de coordenadas pela translação do sistema cartesiano. Identificar uma cônica transladada a partir da
Aula 8 Cônicas - Translação de sistemas de coordenadas MÓDULO 1 - AULA 8 Objetivos Entender a mudança de coordenadas pela translação do sistema cartesiano. Identificar uma cônica transladada a partir da
Aula 14 Círculo. Objetivos
 Aula 1 Círculo MÓDULO 1 - AULA 1 Objetivos Determinar a equação do círculo de centro C e raio r, como um lugar geométrico. Aprender os conceitos de retas tangente e normal num ponto P de um círculo. Esboçar
Aula 1 Círculo MÓDULO 1 - AULA 1 Objetivos Determinar a equação do círculo de centro C e raio r, como um lugar geométrico. Aprender os conceitos de retas tangente e normal num ponto P de um círculo. Esboçar
Aula 19 Elipse - continuação
 MÓDULO 1 - AULA 19 Aula 19 Elipse - continuação Objetivos Desenhar a elipse com compasso e régua com escala. Determinar a equação reduzida da elipse no sistema de coordenadas com origem no ponto médio
MÓDULO 1 - AULA 19 Aula 19 Elipse - continuação Objetivos Desenhar a elipse com compasso e régua com escala. Determinar a equação reduzida da elipse no sistema de coordenadas com origem no ponto médio
Aula 2 A distância no espaço
 MÓDULO 1 - AULA 2 Objetivos Aula 2 A distância no espaço Determinar a distância entre dois pontos do espaço. Estabelecer a equação da esfera em termos de distância. Estudar a posição relativa entre duas
MÓDULO 1 - AULA 2 Objetivos Aula 2 A distância no espaço Determinar a distância entre dois pontos do espaço. Estabelecer a equação da esfera em termos de distância. Estudar a posição relativa entre duas
Aula Elipse. Definição 1. Nosso objetivo agora é estudar a equação geral do segundo grau em duas variáveis:
 Aula 18 Nosso objetivo agora é estudar a equação geral do segundo grau em duas variáveis: Ax + Bxy + Cy + Dx + Ey + F = 0, onde A 0 ou B 0 ou C 0 Vamos considerar primeiro os casos em que B = 0. Isto é,
Aula 18 Nosso objetivo agora é estudar a equação geral do segundo grau em duas variáveis: Ax + Bxy + Cy + Dx + Ey + F = 0, onde A 0 ou B 0 ou C 0 Vamos considerar primeiro os casos em que B = 0. Isto é,
Geometria Analítica - Aula
 Geometria Analítica - Aula 19 246 IM-UFF K. Frensel - J. Delgado Aula 20 Vamos analisar a equação Ax 2 + Cy 2 + Dx + Ey + F = 0 nos casos em que exatamente um dos coeficientes A ou C é nulo. 1. Parábola
Geometria Analítica - Aula 19 246 IM-UFF K. Frensel - J. Delgado Aula 20 Vamos analisar a equação Ax 2 + Cy 2 + Dx + Ey + F = 0 nos casos em que exatamente um dos coeficientes A ou C é nulo. 1. Parábola
Aula Exemplos diversos. Exemplo 1
 Aula 3 1. Exemplos diversos Exemplo 1 Determine a equação da hipérbole equilátera, H, que passa pelo ponto Q = ( 1, ) e tem os eixos coordenados como assíntotas. Como as assíntotas da hipérbole são os
Aula 3 1. Exemplos diversos Exemplo 1 Determine a equação da hipérbole equilátera, H, que passa pelo ponto Q = ( 1, ) e tem os eixos coordenados como assíntotas. Como as assíntotas da hipérbole são os
Aula 17 Superfícies quádricas - parabolóides
 Objetivos Aula 17 Superfícies quádricas - parabolóides Apresentar os parabolóides elípticos e hiperbólicos identificando suas seções planas. Estudar os parabolóides regrados e de revolução. Nas superfícies
Objetivos Aula 17 Superfícies quádricas - parabolóides Apresentar os parabolóides elípticos e hiperbólicos identificando suas seções planas. Estudar os parabolóides regrados e de revolução. Nas superfícies
Aula 15 Superfícies quádricas - cones quádricos
 Aula 15 Superfícies quádricas - cones quádricos MÓDULO - AULA 15 Objetivos Definir e estudar os cones quádricos identificando suas seções planas. Analisar os cones quádricos regrados e de revolução. Cones
Aula 15 Superfícies quádricas - cones quádricos MÓDULO - AULA 15 Objetivos Definir e estudar os cones quádricos identificando suas seções planas. Analisar os cones quádricos regrados e de revolução. Cones
Aula 10 Produto interno, vetorial e misto -
 MÓDULO 2 - AULA 10 Aula 10 Produto interno, vetorial e misto - Aplicações II Objetivos Estudar as posições relativas entre retas no espaço. Obter as expressões para calcular distância entre retas. Continuando
MÓDULO 2 - AULA 10 Aula 10 Produto interno, vetorial e misto - Aplicações II Objetivos Estudar as posições relativas entre retas no espaço. Obter as expressões para calcular distância entre retas. Continuando
0 < c < a ; d(f 1, F 2 ) = 2c
 Capítulo 14 Elipse Nosso objetivo, neste e nos próximos capítulos, é estudar a equação geral do segundo grau em duas variáveis: Ax + Bxy + Cy + Dx + Ey + F = 0, onde A 0 ou B 0 ou C 0 Para isso, deniremos,
Capítulo 14 Elipse Nosso objetivo, neste e nos próximos capítulos, é estudar a equação geral do segundo grau em duas variáveis: Ax + Bxy + Cy + Dx + Ey + F = 0, onde A 0 ou B 0 ou C 0 Para isso, deniremos,
Geometria Analítica - Aula
 Geometria Analítica - Aula 18 228 IM-UFF K. Frensel - J. Delgado Aula 19 Continuamos com o nosso estudo da equação Ax 2 + Cy 2 + Dx + Ey + F = 0 1. Hipérbole Definição 1 Uma hipérbole, H, de focos F 1
Geometria Analítica - Aula 18 228 IM-UFF K. Frensel - J. Delgado Aula 19 Continuamos com o nosso estudo da equação Ax 2 + Cy 2 + Dx + Ey + F = 0 1. Hipérbole Definição 1 Uma hipérbole, H, de focos F 1
Posição relativa entre retas e círculos e distâncias
 4 Posição relativa entre retas e círculos e distâncias Sumário 4.1 Distância de um ponto a uma reta.......... 2 4.2 Posição relativa de uma reta e um círculo no plano 4 4.3 Distância entre duas retas no
4 Posição relativa entre retas e círculos e distâncias Sumário 4.1 Distância de um ponto a uma reta.......... 2 4.2 Posição relativa de uma reta e um círculo no plano 4 4.3 Distância entre duas retas no
J. Delgado - K. Frensel - L. Crissaff Geometria Analítica e Cálculo Vetorial
 76 Capítulo 4 Distâncias no plano e regiões no plano 1. Distância de um ponto a uma reta Dados um ponto P e uma reta r no plano, já sabemos calcular a distância de P a cada ponto P r. Definição 1 Definimos
76 Capítulo 4 Distâncias no plano e regiões no plano 1. Distância de um ponto a uma reta Dados um ponto P e uma reta r no plano, já sabemos calcular a distância de P a cada ponto P r. Definição 1 Definimos
Geometria Analítica II - Aula 4 82
 Geometria Analítica II - Aula 4 8 IM-UFF K. Frensel - J. Delgado Aula 5 Esferas Iniciaremos o nosso estudo sobre superfícies com a esfera, que já nos é familiar. A esfera S de centro no ponto A e raio
Geometria Analítica II - Aula 4 8 IM-UFF K. Frensel - J. Delgado Aula 5 Esferas Iniciaremos o nosso estudo sobre superfícies com a esfera, que já nos é familiar. A esfera S de centro no ponto A e raio
Aula 10 Regiões e inequações no plano
 MÓDULO 1 - AULA 10 Aula 10 Regiões e inequações no plano Objetivos Resolver inequações do segundo grau. Analisar sistemas envolvendo inequações do primeiro e segundo graus. Resolver inequações modulares
MÓDULO 1 - AULA 10 Aula 10 Regiões e inequações no plano Objetivos Resolver inequações do segundo grau. Analisar sistemas envolvendo inequações do primeiro e segundo graus. Resolver inequações modulares
Capítulo Coordenadas no Espaço. Seja E o espaço da Geometria Euclidiana tri-dimensional.
 Capítulo 9 1. Coordenadas no Espaço Seja E o espaço da Geometria Euclidiana tri-dimensional. Um sistema de eixos ortogonais OXY Z em E consiste de três eixos ortogonais entre si OX, OY e OZ com a mesma
Capítulo 9 1. Coordenadas no Espaço Seja E o espaço da Geometria Euclidiana tri-dimensional. Um sistema de eixos ortogonais OXY Z em E consiste de três eixos ortogonais entre si OX, OY e OZ com a mesma
Capítulo 2. Retas no plano. 1. Retas verticais e não-verticais. Definição 1
 Capítulo 2 Retas no plano O objetivo desta aula é determinar a equação algébrica que representa uma reta no plano. Para isso, vamos analisar separadamente dois tipos de reta: reta vertical e reta não-vertical.
Capítulo 2 Retas no plano O objetivo desta aula é determinar a equação algébrica que representa uma reta no plano. Para isso, vamos analisar separadamente dois tipos de reta: reta vertical e reta não-vertical.
Distância entre duas retas. Regiões no plano
 Capítulo 4 Distância entre duas retas. Regiões no plano Nesta aula, veremos primeiro como podemos determinar a distância entre duas retas paralelas no plano. Para isso, lembramos que, na aula anterior,
Capítulo 4 Distância entre duas retas. Regiões no plano Nesta aula, veremos primeiro como podemos determinar a distância entre duas retas paralelas no plano. Para isso, lembramos que, na aula anterior,
Obter as equações paramétricas das cônicas.
 MÓDULO 1 - AULA 1 Aula 1 Equações paramétricas das cônicas Objetivo Obter as equações paramétricas das cônicas. Estudando as retas no plano, você viu que a reta s, determinada pelos pontos P = (x 1, y
MÓDULO 1 - AULA 1 Aula 1 Equações paramétricas das cônicas Objetivo Obter as equações paramétricas das cônicas. Estudando as retas no plano, você viu que a reta s, determinada pelos pontos P = (x 1, y
J. Delgado - K. Frensel - L. Crissaff Geometria Analítica e Cálculo Vetorial
 178 Capítulo 10 Equação da reta e do plano no espaço 1. Equações paramétricas da reta no espaço Sejam A e B dois pontos distintos no espaço e seja r a reta que os contém. Então, P r existe t R tal que
178 Capítulo 10 Equação da reta e do plano no espaço 1. Equações paramétricas da reta no espaço Sejam A e B dois pontos distintos no espaço e seja r a reta que os contém. Então, P r existe t R tal que
Coordenadas e distância na reta e no plano
 Capítulo 1 Coordenadas e distância na reta e no plano 1. Introdução A Geometria Analítica nos permite representar pontos da reta por números reais, pontos do plano por pares ordenados de números reais
Capítulo 1 Coordenadas e distância na reta e no plano 1. Introdução A Geometria Analítica nos permite representar pontos da reta por números reais, pontos do plano por pares ordenados de números reais
Geometria Analítica II - Aula 5 108
 Geometria Analítica II - Aula 5 108 IM-UFF Aula 6 Superfícies Cilíndricas Sejam γ uma curva contida num plano π do espaço e v 0 um vetor não-paralelo ao plano π. A superfície cilíndrica S de diretriz γ
Geometria Analítica II - Aula 5 108 IM-UFF Aula 6 Superfícies Cilíndricas Sejam γ uma curva contida num plano π do espaço e v 0 um vetor não-paralelo ao plano π. A superfície cilíndrica S de diretriz γ
MÓDULO 1 - AULA 21. Objetivos
 Aula 1 Hipérbole - continuação Objetivos Aprender a desenhar a hipérbole com compasso e régua com escala. Determinar a equação reduzida da hipérbole no sistema de coordenadas com origem no ponto médio
Aula 1 Hipérbole - continuação Objetivos Aprender a desenhar a hipérbole com compasso e régua com escala. Determinar a equação reduzida da hipérbole no sistema de coordenadas com origem no ponto médio
Equações paramétricas das cônicas
 Aula 1 Equações paramétricas das cônicas Ao estudarmos as retas no plano, vimos que a reta r que passa por dois pontos distintos P 1 = x 1, y 1 ) e P = x, y ) é dada pelas seguintes equações paramétricas:
Aula 1 Equações paramétricas das cônicas Ao estudarmos as retas no plano, vimos que a reta r que passa por dois pontos distintos P 1 = x 1, y 1 ) e P = x, y ) é dada pelas seguintes equações paramétricas:
Ricardo Bianconi. Fevereiro de 2015
 Seções Cônicas Ricardo Bianconi Fevereiro de 2015 Uma parte importante da Geometria Analítica é o estudo das curvas planas e, em particular, das cônicas. Neste texto estudamos algumas propriedades das
Seções Cônicas Ricardo Bianconi Fevereiro de 2015 Uma parte importante da Geometria Analítica é o estudo das curvas planas e, em particular, das cônicas. Neste texto estudamos algumas propriedades das
Geometria Analítica I
 Geom. Analítica I Respostas do Módulo I - Aula 7 1 Geometria Analítica I 01/03/2011 Respostas dos Exercícios do Módulo I - Aula 7 Aula 7 1. a. Procedendo como nos Exemplos 7.1 e 7.2, ou a Proposição 7.15
Geom. Analítica I Respostas do Módulo I - Aula 7 1 Geometria Analítica I 01/03/2011 Respostas dos Exercícios do Módulo I - Aula 7 Aula 7 1. a. Procedendo como nos Exemplos 7.1 e 7.2, ou a Proposição 7.15
Aula 3 A Reta e a Dependência Linear
 MÓDULO 1 - AULA 3 Aula 3 A Reta e a Dependência Linear Objetivos Determinar a equação paramétrica de uma reta no plano. Compreender o paralelismo entre retas e vetores. Entender a noção de dependência
MÓDULO 1 - AULA 3 Aula 3 A Reta e a Dependência Linear Objetivos Determinar a equação paramétrica de uma reta no plano. Compreender o paralelismo entre retas e vetores. Entender a noção de dependência
Concluimos dai que o centro da circunferência é C = (6, 4) e o raio é
 QUESTÕES-AULA 17 1. A equação x 2 + y 2 12x + 8y + 0 = 0 representa uma circunferência de centro C = (a, b) e de raio R. Determinar o valor de a + b + R. Solução Completamos quadrados na expressão dada.
QUESTÕES-AULA 17 1. A equação x 2 + y 2 12x + 8y + 0 = 0 representa uma circunferência de centro C = (a, b) e de raio R. Determinar o valor de a + b + R. Solução Completamos quadrados na expressão dada.
Aula 4. Coordenadas polares. Definição 1. Observação 1
 Aula Coordenadas polares Nesta aula veremos que há outra maneira de expressar a posição de um ponto no plano, distinta da forma cartesiana Embora os sistemas cartesianos sejam muito utilizados, há curvas
Aula Coordenadas polares Nesta aula veremos que há outra maneira de expressar a posição de um ponto no plano, distinta da forma cartesiana Embora os sistemas cartesianos sejam muito utilizados, há curvas
Aula 18 Cilindros quádricos e identificação de quádricas
 MÓDULO 2 - AULA 18 Aula 18 Cilindros quádricos e identificação de quádricas Objetivos Estudar os cilindros quádricos, analisando suas seções planas paralelas aos planos coordenados e estabelecendo suas
MÓDULO 2 - AULA 18 Aula 18 Cilindros quádricos e identificação de quádricas Objetivos Estudar os cilindros quádricos, analisando suas seções planas paralelas aos planos coordenados e estabelecendo suas
Retas e círculos, posições relativas e distância de um ponto a uma reta
 Capítulo 3 Retas e círculos, posições relativas e distância de um ponto a uma reta Nesta aula vamos caracterizar de forma algébrica a posição relativa de duas retas no plano e de uma reta e de um círculo
Capítulo 3 Retas e círculos, posições relativas e distância de um ponto a uma reta Nesta aula vamos caracterizar de forma algébrica a posição relativa de duas retas no plano e de uma reta e de um círculo
Aula Distância entre duas retas paralelas no espaço. Definição 1. Exemplo 1
 Aula 1 Sejam r 1 = P 1 + t v 1 t R} e r 2 = P 2 + t v 2 t R} duas retas no espaço. Se r 1 r 2, sabemos que r 1 e r 2 são concorrentes (isto é r 1 r 2 ) ou não se intersectam. Quando a segunda possibilidade
Aula 1 Sejam r 1 = P 1 + t v 1 t R} e r 2 = P 2 + t v 2 t R} duas retas no espaço. Se r 1 r 2, sabemos que r 1 e r 2 são concorrentes (isto é r 1 r 2 ) ou não se intersectam. Quando a segunda possibilidade
Preliminares de Cálculo
 Preliminares de Cálculo Profs. Ulysses Sodré e Olivio Augusto Weber Londrina, 21 de Fevereiro de 2008, arquivo: precalc.tex... Conteúdo 1 Números reais 2 1.1 Algumas propriedades do corpo R dos números
Preliminares de Cálculo Profs. Ulysses Sodré e Olivio Augusto Weber Londrina, 21 de Fevereiro de 2008, arquivo: precalc.tex... Conteúdo 1 Números reais 2 1.1 Algumas propriedades do corpo R dos números
Aula 15 Parábola. Objetivos
 MÓDULO 1 - AULA 15 Aula 15 Parábola Objetivos Descrever a parábola como um lugar geométrico determinando a sua equação reduzida nos sistemas de coordenadas com eixo x paralelo à diretriz l e origem no
MÓDULO 1 - AULA 15 Aula 15 Parábola Objetivos Descrever a parábola como um lugar geométrico determinando a sua equação reduzida nos sistemas de coordenadas com eixo x paralelo à diretriz l e origem no
Elipse. Sumário. 5.1 Introdução Elipse Forma canônica da elipse Elipse com centro na origem e reta focal coincidente
 5 Elipse Sumário 5.1 Introdução....................... 5. Elipse.......................... 3 5.3 Forma canônica da elipse............... 6 5.3.1 Elipse E com centro na origem e reta focal coincidente com
5 Elipse Sumário 5.1 Introdução....................... 5. Elipse.......................... 3 5.3 Forma canônica da elipse............... 6 5.3.1 Elipse E com centro na origem e reta focal coincidente com
Aula 9 Cônicas - Rotação de sistemas de coordenadas
 MÓDULO 1 - AULA 9 Aula 9 Cônicas - Rotação de sistemas de coordenadas Objetivos Entender mudanças de coordenadas por rotações. Identificar uma cônica rotacionada a partir da sua equação geral. Identificar
MÓDULO 1 - AULA 9 Aula 9 Cônicas - Rotação de sistemas de coordenadas Objetivos Entender mudanças de coordenadas por rotações. Identificar uma cônica rotacionada a partir da sua equação geral. Identificar
Hipérbole. Sumário. 6.1 Introdução Hipérbole Forma canônica da hipérbole... 6
 6 Hipérbole Sumário 6.1 Introdução....................... 2 6.2 Hipérbole........................ 2 6.3 Forma canônica da hipérbole............. 6 6.3.1 Hipérbole com centro na origem e reta focal coincidente
6 Hipérbole Sumário 6.1 Introdução....................... 2 6.2 Hipérbole........................ 2 6.3 Forma canônica da hipérbole............. 6 6.3.1 Hipérbole com centro na origem e reta focal coincidente
MAT Poli Cônicas - Parte I
 MAT2454 - Poli - 2011 Cônicas - Parte I Uma equação quadrática em duas variáveis, x e y, é uma equação da forma ax 2 +by 2 +cxy +dx+ey +f = 0, em que pelo menos um doscoeficientes a, b oucénão nulo 1.
MAT2454 - Poli - 2011 Cônicas - Parte I Uma equação quadrática em duas variáveis, x e y, é uma equação da forma ax 2 +by 2 +cxy +dx+ey +f = 0, em que pelo menos um doscoeficientes a, b oucénão nulo 1.
Material Teórico - Módulo Cônicas. Elipses. Terceiro Ano do Ensino Médio
 Material Teórico - Módulo Cônicas Elipses Terceiro Ano do Ensino Médio Autor: Prof. Fabrício Siqueira Benevides Revisor: Prof. Antonio Caminha M. Neto 1 Introdução Conforme mencionamos na primeira aula
Material Teórico - Módulo Cônicas Elipses Terceiro Ano do Ensino Médio Autor: Prof. Fabrício Siqueira Benevides Revisor: Prof. Antonio Caminha M. Neto 1 Introdução Conforme mencionamos na primeira aula
Geometria Analítica II - Aula 7 178
 Geometria Analítica II - Aula 7 178 Aula 8 Superfícies Regradas Dizemos que uma superfície S é regrada quando por todo ponto P pertencente a S passa pelo menos uma reta r P inteiramente contida em S. Fig.
Geometria Analítica II - Aula 7 178 Aula 8 Superfícies Regradas Dizemos que uma superfície S é regrada quando por todo ponto P pertencente a S passa pelo menos uma reta r P inteiramente contida em S. Fig.
Matemática I Cálculo I Unidade B - Cônicas. Profª Msc. Débora Bastos. IFRS Campus Rio Grande FURG UNIVERSIDADE FEDERAL DO RIO GRANDE
 Unidade B - Cônicas Profª Msc. Débora Bastos IFRS Campus Rio Grande FURG UNIVERSIDADE FEDERAL DO RIO GRANDE 22 12. Cônicas São chamadas cônicas as curvas resultantes do corte de um cone duplo com um plano.
Unidade B - Cônicas Profª Msc. Débora Bastos IFRS Campus Rio Grande FURG UNIVERSIDADE FEDERAL DO RIO GRANDE 22 12. Cônicas São chamadas cônicas as curvas resultantes do corte de um cone duplo com um plano.
2 As Cônicas. estudos da Geometria, tornou-se um dos mais originais matemáticos gregos.
 2 As Cônicas Segundo Delgado, Frensel e Crissaff (2013), historiadores creditam ao matemático grego Menaecmus (380 a. C 320 a.c.) a descoberta do estudo das Curvas Cônicas. Acredita-se que o referido geômetra
2 As Cônicas Segundo Delgado, Frensel e Crissaff (2013), historiadores creditam ao matemático grego Menaecmus (380 a. C 320 a.c.) a descoberta do estudo das Curvas Cônicas. Acredita-se que o referido geômetra
21 e 22. Superfícies Quádricas. Sumário
 21 e 22 Superfícies uádricas Sumário 21.1 Introdução....................... 2 21.2 Elipsoide........................ 3 21.3 Hiperboloide de uma Folha.............. 4 21.4 Hiperboloide de duas folhas..............
21 e 22 Superfícies uádricas Sumário 21.1 Introdução....................... 2 21.2 Elipsoide........................ 3 21.3 Hiperboloide de uma Folha.............. 4 21.4 Hiperboloide de duas folhas..............
1. A partir da definição, determinar a equação da parábola P, cujo foco é F = (3, 4) e cuja diretriz é L : x + y 2 = 0. (x 3) 2 + (y + 4) 2 =
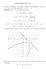 QUESTÕES-AULA 18 1. A partir da definição, determinar a equação da parábola P, cujo foco é F = (3, 4) e cuja diretriz é L : x + y = 0. Solução Seja P = (x, y) R. Temos que P P d(p, F ) = d(p, L) (x 3)
QUESTÕES-AULA 18 1. A partir da definição, determinar a equação da parábola P, cujo foco é F = (3, 4) e cuja diretriz é L : x + y = 0. Solução Seja P = (x, y) R. Temos que P P d(p, F ) = d(p, L) (x 3)
Geometria Analítica I
 Geom. Analítica I Respostas do Módulo I - Aula 11 1 Geometria Analítica I 10/05/011 Respostas dos Exercícios do Módulo I - Aula 11 Aula 11 1. Em todos os itens desta questão, utilizaremos as relações x
Geom. Analítica I Respostas do Módulo I - Aula 11 1 Geometria Analítica I 10/05/011 Respostas dos Exercícios do Módulo I - Aula 11 Aula 11 1. Em todos os itens desta questão, utilizaremos as relações x
CÔNICAS - MAT CÁLCULO II - Bacharelado Química - Diurno 2 o SEMESTRE de 2009 Professor Oswaldo Rio Branco ELIPSE
 CÔNICAS - MAT 2127 - CÁLCULO II - Bacharelado Química - Diurno 2 o SEMESTRE de 2009 Professor Oswaldo Rio Branco No plano euclidiano consideremos F 1 e F 2 dois pontos (focos) distintos. ELIPSE (1) Se
CÔNICAS - MAT 2127 - CÁLCULO II - Bacharelado Química - Diurno 2 o SEMESTRE de 2009 Professor Oswaldo Rio Branco No plano euclidiano consideremos F 1 e F 2 dois pontos (focos) distintos. ELIPSE (1) Se
Capítulo 1. Conjuntos e Relações. 1.1 Noção intuitiva de conjuntos. Notação dos conjuntos
 Conjuntos e Relações Capítulo Neste capítulo você deverá: Identificar e escrever os tipos de conjuntos, tais como, conjunto vazio, unitário, finito, infinito, os conjuntos numéricos, a reta numérica e
Conjuntos e Relações Capítulo Neste capítulo você deverá: Identificar e escrever os tipos de conjuntos, tais como, conjunto vazio, unitário, finito, infinito, os conjuntos numéricos, a reta numérica e
Objetivos. Aprender a propriedade reflexiva da parábola.
 Aula 16 Parábola - continuação MÓDULO 1 - AULA 16 Objetivos Descrever a parábola como um lugar geométrico, determinando a sua equação reduzida nos sistemas de coordenadas com eixo y paralelo à diretriz
Aula 16 Parábola - continuação MÓDULO 1 - AULA 16 Objetivos Descrever a parábola como um lugar geométrico, determinando a sua equação reduzida nos sistemas de coordenadas com eixo y paralelo à diretriz
Volume III: Geometria Analítica Espacial. Jorge Delgado Katia Frensel Nedir do Espírito Santo (IMUFF) (IMUFF) (IMUFRJ)
 Volume III: Geometria Analítica Espacial Jorge Delgado Katia Frensel Nedir do Espírito Santo (IMUFF) (IMUFF) (IMUFRJ) C E D E R J 2 Conteúdo 5 C E D E R J 6 Módulo 3 Geometria Analítica Espacial... o princípio
Volume III: Geometria Analítica Espacial Jorge Delgado Katia Frensel Nedir do Espírito Santo (IMUFF) (IMUFF) (IMUFRJ) C E D E R J 2 Conteúdo 5 C E D E R J 6 Módulo 3 Geometria Analítica Espacial... o princípio
Objetivos. Expressar o vértice da parábola em termos do discriminante e dos
 MÓDULO 1 - AULA 17 Aula 17 Parábola - aplicações Objetivos Expressar o vértice da parábola em termos do discriminante e dos coeficientes da equação quadrática Expressar as raízes das equações quadráticas
MÓDULO 1 - AULA 17 Aula 17 Parábola - aplicações Objetivos Expressar o vértice da parábola em termos do discriminante e dos coeficientes da equação quadrática Expressar as raízes das equações quadráticas
Geometria Analítica I
 Geom. Analítica I Respostas do Módulo I - Aula 14 1 Geometria Analítica I 10/03/011 Respostas dos Exercícios do Módulo I - Aula 14 Aula 14 1. a. A equação do círculo de centro h, k) e raio r é x h) + y
Geom. Analítica I Respostas do Módulo I - Aula 14 1 Geometria Analítica I 10/03/011 Respostas dos Exercícios do Módulo I - Aula 14 Aula 14 1. a. A equação do círculo de centro h, k) e raio r é x h) + y
Aula 5 Equações paramétricas de retas e planos
 Aula 5 Equações paramétricas de retas e planos MÓDULO 1 - AULA 5 Objetivo Estabelecer as equações paramétricas de retas e planos no espaço usando dados diversos. Na Aula 3, do Módulo 1, vimos como determinar
Aula 5 Equações paramétricas de retas e planos MÓDULO 1 - AULA 5 Objetivo Estabelecer as equações paramétricas de retas e planos no espaço usando dados diversos. Na Aula 3, do Módulo 1, vimos como determinar
Notas de Aulas 3 - Cônicas Prof Carlos A S Soares
 Notas de Aulas 3 - Cônicas Prof Carlos A S Soares 1 Parábolas 1.1 Conceito e Elementos Definição 1.1 Sejam l uma reta e F um ponto não pertencente a l. Chamamos parábola de diretriz l e foco F o conjunto
Notas de Aulas 3 - Cônicas Prof Carlos A S Soares 1 Parábolas 1.1 Conceito e Elementos Definição 1.1 Sejam l uma reta e F um ponto não pertencente a l. Chamamos parábola de diretriz l e foco F o conjunto
Aula 6 Produto interno
 MÓDULO 1 - AULA 6 Objetivos Aula 6 Produto interno Estabelecer os conceitos de norma de um vetor e de ângulo entre dois vetores do espaço. Definir o produto interno de vetores no espaço e estabelecer suas
MÓDULO 1 - AULA 6 Objetivos Aula 6 Produto interno Estabelecer os conceitos de norma de um vetor e de ângulo entre dois vetores do espaço. Definir o produto interno de vetores no espaço e estabelecer suas
Capítulo Equações da reta no espaço. Sejam A e B dois pontos distintos no espaço e seja r a reta que os contém. Então, P r existe t R tal que
 Capítulo 11 1. Equações da reta no espaço Sejam A e B dois pontos distintos no espaço e seja r a reta que os contém. Então, P r existe t R tal que AP = t AB Fig. 1: Reta r passando por A e B. Como o ponto
Capítulo 11 1. Equações da reta no espaço Sejam A e B dois pontos distintos no espaço e seja r a reta que os contém. Então, P r existe t R tal que AP = t AB Fig. 1: Reta r passando por A e B. Como o ponto
Aula 4 Colinearidade, coplanaridade e dependência linear
 Aula 4 Colinearidade, coplanaridade e dependência linear MÓDULO 1 - AULA 4 Objetivos Compreender os conceitos de independência e dependência linear. Estabelecer condições para determinar quando uma coleção
Aula 4 Colinearidade, coplanaridade e dependência linear MÓDULO 1 - AULA 4 Objetivos Compreender os conceitos de independência e dependência linear. Estabelecer condições para determinar quando uma coleção
A primeira coisa a fazer é saber quais são as equações das curvas quando elas já se encontram na melhor
 Identificação de Cônicas Uma equação do segundo grau ax + bxy + cy + dx + ey + f = 0 define de maneira implícita uma curva no plano xy: o conjunto dos pontos (x, y) que satisfazem a equação. Por exemplo,
Identificação de Cônicas Uma equação do segundo grau ax + bxy + cy + dx + ey + f = 0 define de maneira implícita uma curva no plano xy: o conjunto dos pontos (x, y) que satisfazem a equação. Por exemplo,
6. FUNÇÃO QUADRÁTICA 6.1. CONSIDERAÇÕES PRELIMINARES
 47 6. FUNÇÃO QUADRÁTICA 6.1. CONSIDERAÇÕES PRELIMINARES Na figura abaixo, seja a reta r e o ponto F de um determinado plano, tal que F não pertence a r. Consideremos as seguintes questões: Podemos obter,
47 6. FUNÇÃO QUADRÁTICA 6.1. CONSIDERAÇÕES PRELIMINARES Na figura abaixo, seja a reta r e o ponto F de um determinado plano, tal que F não pertence a r. Consideremos as seguintes questões: Podemos obter,
Plano cartesiano, Retas e. Alex Oliveira. Circunferência
 Plano cartesiano, Retas e Alex Oliveira Circunferência Sistema cartesiano ortogonal O sistema cartesiano ortogonal é formado por dois eixos ortogonais(eixo x e eixo y). A intersecção dos eixos x e y é
Plano cartesiano, Retas e Alex Oliveira Circunferência Sistema cartesiano ortogonal O sistema cartesiano ortogonal é formado por dois eixos ortogonais(eixo x e eixo y). A intersecção dos eixos x e y é
Geometria Analítica I
 Geom. Analítica I Respostas do Módulo I - Aula 15 1 Geometria Analítica I 17/03/2011 Respostas dos Exercícios do Módulo I - Aula 15 Aula 15 1. Este exercício se resume a escrever a equação em uma das formas
Geom. Analítica I Respostas do Módulo I - Aula 15 1 Geometria Analítica I 17/03/2011 Respostas dos Exercícios do Módulo I - Aula 15 Aula 15 1. Este exercício se resume a escrever a equação em uma das formas
Curvas Planas em Coordenadas Polares
 Curvas Planas em Coordenadas Polares Sumário. Coordenadas Polares.................... Relações entre coordenadas polares e coordenadas cartesianas...................... 6. Exercícios........................
Curvas Planas em Coordenadas Polares Sumário. Coordenadas Polares.................... Relações entre coordenadas polares e coordenadas cartesianas...................... 6. Exercícios........................
54 CAPÍTULO 2. GEOMETRIA ANALÍTICA ( ) =
 54 CAPÍTULO. GEOMETRIA ANALÍTICA.5 Cônicas O grá co da equação + + + + + = 0 (.4) onde,,,, e são constantes com, e, não todos nulos, é uma cônica. A equação (.4) é chamada de equação geral do grau em e
54 CAPÍTULO. GEOMETRIA ANALÍTICA.5 Cônicas O grá co da equação + + + + + = 0 (.4) onde,,,, e são constantes com, e, não todos nulos, é uma cônica. A equação (.4) é chamada de equação geral do grau em e
Universidade Federal do Pará Curso de Licenciatura em Matemática PARFOR Lista de Exercícios Referentes a Prova Substitutiva de Geometria Analítica
 1 Universidade Federal do Pará Curso de Licenciatura em Matemática PARFOR Lista de Exercícios Referentes a Prova Substitutiva de Geometria Analítica 1. Determine a distância entre os pontos A(-2, 7) e
1 Universidade Federal do Pará Curso de Licenciatura em Matemática PARFOR Lista de Exercícios Referentes a Prova Substitutiva de Geometria Analítica 1. Determine a distância entre os pontos A(-2, 7) e
Aula 4 Produto Interno
 MÓDULO 1 - AULA 4 Objetivos Aula 4 Produto Interno Definir as noções de ângulo entre dois vetores, a norma de um vetor e a operação de produto interno. Compreender as propriedades básicas da norma e do
MÓDULO 1 - AULA 4 Objetivos Aula 4 Produto Interno Definir as noções de ângulo entre dois vetores, a norma de um vetor e a operação de produto interno. Compreender as propriedades básicas da norma e do
MATRIZES VETORES E GEOMETRIA. Reginaldo J. Santos Departamento de Matemática-ICEx Universidade Federal de Minas Gerais
 MATRIZES VETORES E GEOMETRIA ANALÍTICA Departamento de Matemática-ICEx Universidade Federal de Minas Gerais http://www.mat.ufmg.br/~regi Março 2002 Matrizes Vetores e Geometria Anaĺıtica Copyright c 2002
MATRIZES VETORES E GEOMETRIA ANALÍTICA Departamento de Matemática-ICEx Universidade Federal de Minas Gerais http://www.mat.ufmg.br/~regi Março 2002 Matrizes Vetores e Geometria Anaĺıtica Copyright c 2002
Aula Exemplos e aplicações - continuação. Exemplo 8. Nesta aula continuamos com mais exemplos e aplicações dos conceitos vistos.
 Aula 1 Nesta aula continuamos com mais exemplos e aplicações dos conceitos vistos. 1. Exemplos e aplicações - continuação Exemplo 8 Considere o plano π : x + y + z = 3 e a reta r paralela ao vetor v =
Aula 1 Nesta aula continuamos com mais exemplos e aplicações dos conceitos vistos. 1. Exemplos e aplicações - continuação Exemplo 8 Considere o plano π : x + y + z = 3 e a reta r paralela ao vetor v =
Capítulo 3 - Geometria Analítica
 1. Gráficos de Equações Capítulo 3 - Geometria Analítica Conceito:O gráfico de uma equação é o conjunto de todos os pontos e somente estes pontos, cujas coordenadas satisfazem a equação. Assim, o gráfico
1. Gráficos de Equações Capítulo 3 - Geometria Analítica Conceito:O gráfico de uma equação é o conjunto de todos os pontos e somente estes pontos, cujas coordenadas satisfazem a equação. Assim, o gráfico
Geometria Analítica. Katia Frensel - Jorge Delgado. NEAD - Núcleo de Educação a Distância. Curso de Licenciatura em Matemática UFMA
 Geometria Analítica NEAD - Núcleo de Educação a Distância Curso de Licenciatura em Matemática UFMA Katia Frensel - Jorge Delgado Março, 2011 ii Geometria Analítica Conteúdo Prefácio ix 1 Coordenadas na
Geometria Analítica NEAD - Núcleo de Educação a Distância Curso de Licenciatura em Matemática UFMA Katia Frensel - Jorge Delgado Março, 2011 ii Geometria Analítica Conteúdo Prefácio ix 1 Coordenadas na
Este trabalho foi licenciado com a Licença Creative Commons Atribuição - NãoComercial - SemDerivados 3.0 Não Adaptada
 1. Introdução Definição: Parábola é o lugar geométrico dos pontos do plano cujas distâncias entre uma reta fixa, chamada de reta diretriz, e a um ponto fixo situado fora desta reta, chamado de foco da
1. Introdução Definição: Parábola é o lugar geométrico dos pontos do plano cujas distâncias entre uma reta fixa, chamada de reta diretriz, e a um ponto fixo situado fora desta reta, chamado de foco da
GEOMETRIA ANALÍTICA 2017
 GEOMETRIA ANALÍTICA 2017 Tópicos a serem estudados 1) O ponto (Noções iniciais - Reta orientada ou eixo Razão de segmentos Noções Simetria Plano Cartesiano Abcissas e Ordenadas Ponto Médio Baricentro -
GEOMETRIA ANALÍTICA 2017 Tópicos a serem estudados 1) O ponto (Noções iniciais - Reta orientada ou eixo Razão de segmentos Noções Simetria Plano Cartesiano Abcissas e Ordenadas Ponto Médio Baricentro -
Aula 3 Vetores no espaço
 MÓDULO 1 - AULA 3 Aula 3 Vetores no espaço Objetivos Ampliar a noção de vetor para o espaço. Rever as operações com vetores e sua representação em relação a um sistema ortogonal de coordenadas cartesianas.
MÓDULO 1 - AULA 3 Aula 3 Vetores no espaço Objetivos Ampliar a noção de vetor para o espaço. Rever as operações com vetores e sua representação em relação a um sistema ortogonal de coordenadas cartesianas.
10. Determine as equações cartesianas das famílias de retas que fazem um ângulo de π/4 radianos com a reta y = 2x + 1.
 Geometria Analítica. 1. Determine as posições relativas e as interseções entre os conjuntos em R abaixo. Em cada item também faça um esboço dos dois conjuntos dados no mesmo sistema de eixos. (a) C : (x
Geometria Analítica. 1. Determine as posições relativas e as interseções entre os conjuntos em R abaixo. Em cada item também faça um esboço dos dois conjuntos dados no mesmo sistema de eixos. (a) C : (x
Geometria Analítica Plana
 Módulo 1 Geometria Analítica Plana Geometria una et aeterna est in mente Dei refulgens. A Geometria é única e eterna, brilhando na mente de Deus. Conversation with the Sidereal Messenger: carta aberta
Módulo 1 Geometria Analítica Plana Geometria una et aeterna est in mente Dei refulgens. A Geometria é única e eterna, brilhando na mente de Deus. Conversation with the Sidereal Messenger: carta aberta
GGM Geometria Analítica e Cálculo Vetorial Geometria Analítica Básica 20/12/2012- GGM - UFF Dirce Uesu
 GGM0016 Geometria Analítica e Cálculo Vetorial Geometria Analítica Básica 0/1/01- GGM - UFF Dirce Uesu CÔNICAS DEFINIÇÃO GEOMÉTRICA Exercício: Acesse o sitio abaixo e use o programa: http://www.professores.uff.br/hjbortol/disciplinas/005.1/gma04096/applets/conic/co
GGM0016 Geometria Analítica e Cálculo Vetorial Geometria Analítica Básica 0/1/01- GGM - UFF Dirce Uesu CÔNICAS DEFINIÇÃO GEOMÉTRICA Exercício: Acesse o sitio abaixo e use o programa: http://www.professores.uff.br/hjbortol/disciplinas/005.1/gma04096/applets/conic/co
Construções de Dandelin
 Capítulo 7 Construções de Dandelin Na introdução às cônicas como secções planas do cone, referimo-nos às construções de Dandelin. Vamos apresentar estas construções para demonstrar as propriedades da elipse,
Capítulo 7 Construções de Dandelin Na introdução às cônicas como secções planas do cone, referimo-nos às construções de Dandelin. Vamos apresentar estas construções para demonstrar as propriedades da elipse,
Portal OBMEP. Material Teórico - Módulo Cônicas. Terceiro Ano do Ensino Médio
 Material Teórico - Módulo Cônicas Parábolas Terceiro Ano do Ensino Médio Autor: Prof. Fabrício Siqueira Benevides Revisor: Prof. Antonio Caminha M. Neto 1 Introdução ω Nesta aula vamos revisar o conceito
Material Teórico - Módulo Cônicas Parábolas Terceiro Ano do Ensino Médio Autor: Prof. Fabrício Siqueira Benevides Revisor: Prof. Antonio Caminha M. Neto 1 Introdução ω Nesta aula vamos revisar o conceito
Notas de Aulas 3 - Cônicas Prof Carlos A S Soares
 Notas de Aulas 3 - Cônicas Prof Carlos A S Soares 1 Parábolas 11 Conceito e Elementos Definição 1 Sejam l uma reta e F um ponto não pertencente a l Chamamos parábola de diretriz l e foco F o conjunto dos
Notas de Aulas 3 - Cônicas Prof Carlos A S Soares 1 Parábolas 11 Conceito e Elementos Definição 1 Sejam l uma reta e F um ponto não pertencente a l Chamamos parábola de diretriz l e foco F o conjunto dos
54 CAPÍTULO 2. GEOMETRIA ANALÍTICA ( ) =
 54 CAPÍTULO. GEOMETRIA ANALÍTICA.5 Cônicas O grá co da equação + + + + + = 0 (.4) onde,,,, e são constantes com, e, não todos nulos, é uma cônica. A equação (.4) é chamada de equação geral do grau em e
54 CAPÍTULO. GEOMETRIA ANALÍTICA.5 Cônicas O grá co da equação + + + + + = 0 (.4) onde,,,, e são constantes com, e, não todos nulos, é uma cônica. A equação (.4) é chamada de equação geral do grau em e
6.1 equações canônicas de círculos e esferas
 6 C Í R C U LO S E E S F E R A S 6.1 equações canônicas de círculos e esferas Um círculo é o conjunto de pontos no plano que estão a uma certa distância r de um ponto dado (a, b). Desta forma temos que
6 C Í R C U LO S E E S F E R A S 6.1 equações canônicas de círculos e esferas Um círculo é o conjunto de pontos no plano que estão a uma certa distância r de um ponto dado (a, b). Desta forma temos que
1 Cônicas Não Degeneradas
 Seções Cônicas Reginaldo J. Santos Departamento de Matemática-ICE Universidade Federal de Minas Gerais http://www.mat.ufmg.br/~regi regi@mat.ufmg.br 11 de dezembro de 2001 Estudaremos as (seções) cônicas,
Seções Cônicas Reginaldo J. Santos Departamento de Matemática-ICE Universidade Federal de Minas Gerais http://www.mat.ufmg.br/~regi regi@mat.ufmg.br 11 de dezembro de 2001 Estudaremos as (seções) cônicas,
Pré-Cálculo, Vol. 2: Curvas Planas. Jorge J. Delgado Maria Lúcia Torres Villela
 Pré-Cálculo, Vol. 2: Curvas Planas Jorge J. Delgado Maria Lúcia Torres Villela IM-UFF 2007 C E D E R J 2 J. Delgado - M. L. Villela (IM-UFF) Conteúdo 2 Curvas no Plano 7 1. Coordenadas no Plano....................
Pré-Cálculo, Vol. 2: Curvas Planas Jorge J. Delgado Maria Lúcia Torres Villela IM-UFF 2007 C E D E R J 2 J. Delgado - M. L. Villela (IM-UFF) Conteúdo 2 Curvas no Plano 7 1. Coordenadas no Plano....................
Geometria Analítica I - MAT Lista 1 Profa. Lhaylla Crissaff
 1. Entre os pontos A = (4, 0), B = ( 3, 1), C = (0, 7), D = ( 1 2, 0), E = (0, 3) e F = (0, 0), (a) quais estão sobre o eixo OX? (b) quais estão sobre o eixo OY? 2. Descubra qual quadrante está localizado
1. Entre os pontos A = (4, 0), B = ( 3, 1), C = (0, 7), D = ( 1 2, 0), E = (0, 3) e F = (0, 0), (a) quais estão sobre o eixo OX? (b) quais estão sobre o eixo OY? 2. Descubra qual quadrante está localizado
O problema proposto possui alguma solução? Se sim, quantas e quais são elas?
 PROVA PARA OS ALUNOS DE 3º ANO DO ENSINO MÉDIO 1) Considere o seguinte problema: Vitor ganhou R$ 3,20 de seu pai em moedas de 5 centavos, 10 centavos e 25 centavos. Se recebeu um total de 50 moedas, quantas
PROVA PARA OS ALUNOS DE 3º ANO DO ENSINO MÉDIO 1) Considere o seguinte problema: Vitor ganhou R$ 3,20 de seu pai em moedas de 5 centavos, 10 centavos e 25 centavos. Se recebeu um total de 50 moedas, quantas
PLANIFICAÇÃO MODULAR. Ano Letivo 2016/2017
 AGRUPAMENTO DE ESCOLAS DE MIRA Escola Secundária c/3 Dr.ª Maria Cândida CURSO VOCACIONAL CURSO VOCACIONAL DO ENSINO BÁSICO: Jardinagem / Comércio / Socorrismo DISCIPLINA: MATEMÁTICA CICLO DE FORMAÇÃO:
AGRUPAMENTO DE ESCOLAS DE MIRA Escola Secundária c/3 Dr.ª Maria Cândida CURSO VOCACIONAL CURSO VOCACIONAL DO ENSINO BÁSICO: Jardinagem / Comércio / Socorrismo DISCIPLINA: MATEMÁTICA CICLO DE FORMAÇÃO:
Todos os exercícios sugeridos nesta apostila se referem ao volume 3. MATEMÁTICA III 1 ESTUDO DA CIRCUNFERÊNCIA
 DEFINIÇÃO... EQUAÇÃO REDUZIDA... EQUAÇÃO GERAL DA CIRCUNFERÊNCIA... 3 RECONHECIMENTO... 3 POSIÇÃO RELATIVA ENTRE PONTO E CIRCUNFERÊNCIA... 1 POSIÇÃO RELATIVA ENTRE RETA E CIRCUNFERÊNCIA... 17 PROBLEMAS
DEFINIÇÃO... EQUAÇÃO REDUZIDA... EQUAÇÃO GERAL DA CIRCUNFERÊNCIA... 3 RECONHECIMENTO... 3 POSIÇÃO RELATIVA ENTRE PONTO E CIRCUNFERÊNCIA... 1 POSIÇÃO RELATIVA ENTRE RETA E CIRCUNFERÊNCIA... 17 PROBLEMAS
,,,,,,,, e são constantes com,,,, e, não todas nulas. Uma equação desse tipo é a equação de uma quádrica. Observe que a equação
 Capítulo 5 As Superfícies O estudo das superfícies do espaço, iniciado com os planos no capítulo anterior, tem como sequência natural a classi cação das superfícies que podem ser expressas por equações
Capítulo 5 As Superfícies O estudo das superfícies do espaço, iniciado com os planos no capítulo anterior, tem como sequência natural a classi cação das superfícies que podem ser expressas por equações
Equações da reta no plano
 3 Equações da reta no plano Sumário 3.1 Introdução....................... 2 3.2 Equação paramétrica da reta............. 2 3.3 Equação cartesiana da reta.............. 7 3.4 Equação am ou reduzida da reta..........
3 Equações da reta no plano Sumário 3.1 Introdução....................... 2 3.2 Equação paramétrica da reta............. 2 3.3 Equação cartesiana da reta.............. 7 3.4 Equação am ou reduzida da reta..........
Produto interno e produto vetorial no espaço
 14 Produto interno e produto vetorial no espaço Sumário 14.1 Produto interno.................... 14. Produto vetorial.................... 5 14..1 Interpretação geométrica da norma do produto vetorial.......................
14 Produto interno e produto vetorial no espaço Sumário 14.1 Produto interno.................... 14. Produto vetorial.................... 5 14..1 Interpretação geométrica da norma do produto vetorial.......................
CÔNICAS - MAT CÁLCULO 1 - IO Bacharelado Oceanografia - Diurno 1 o semestre de 2010 Professor Oswaldo Rio Branco de Oliveira ELIPSE
 CÔNICAS - MAT 144 - CÁLCULO 1 - IO Bacharelado Oceanografia - Diurno 1 o semestre de 2010 Professor Oswaldo Rio Branco de Oliveira No plano euclidiano consideremos F 1 e F 2 dois pontos (focos) distintos.
CÔNICAS - MAT 144 - CÁLCULO 1 - IO Bacharelado Oceanografia - Diurno 1 o semestre de 2010 Professor Oswaldo Rio Branco de Oliveira No plano euclidiano consideremos F 1 e F 2 dois pontos (focos) distintos.
Capítulo 12. Ângulo entre duas retas no espaço. Definição 1. O ângulo (r1, r2 ) entre duas retas r1 e r2 é assim definido:
 Capítulo 1 1. Ângulo entre duas retas no espaço Definição 1 O ângulo (r1, r ) entre duas retas r1 e r é assim definido: (r1, r ) 0o se r1 e r são coincidentes, se as retas são concorrentes, isto é, r1
Capítulo 1 1. Ângulo entre duas retas no espaço Definição 1 O ângulo (r1, r ) entre duas retas r1 e r é assim definido: (r1, r ) 0o se r1 e r são coincidentes, se as retas são concorrentes, isto é, r1
3.2 Determine a equação da circunferência de raio 5, tangente à reta 3x +4y =16no ponto A (4, 1).
 3.1 Obtenha a equação e esboce o gráfico da circunferência caracterizada por: (a) Centro C (, 1) eraior =5; (b) Passa pelos pontos A (1, ),B(1, 1) e C (, 3) ; (c) Inscrita no triângulo determinado pelas
3.1 Obtenha a equação e esboce o gráfico da circunferência caracterizada por: (a) Centro C (, 1) eraior =5; (b) Passa pelos pontos A (1, ),B(1, 1) e C (, 3) ; (c) Inscrita no triângulo determinado pelas
Geometria Analítica? Onde usar os conhecimentos. os sobre Geometria Analítica?
 X GEOMETRIA ANALÍTICA Por que aprender Geometria Analítica?... A Geometria Analítica estabelece relações entre a álgebra e a geometria por meio de equações e inequações. Isso permite transformar questões
X GEOMETRIA ANALÍTICA Por que aprender Geometria Analítica?... A Geometria Analítica estabelece relações entre a álgebra e a geometria por meio de equações e inequações. Isso permite transformar questões
UNIVERSIDADE FEDERAL DE PERNAMBUCO
 CÁLCULO L1 NOTAS DA PRIMEIRA AULA UNIVERSIDADE FEDERAL DE PERNAMBUCO Resumo. Nesta aula discutiremos como obter as equações das retas tangentes a uma curva planar que é o gráfico de uma função. 1. Introdução
CÁLCULO L1 NOTAS DA PRIMEIRA AULA UNIVERSIDADE FEDERAL DE PERNAMBUCO Resumo. Nesta aula discutiremos como obter as equações das retas tangentes a uma curva planar que é o gráfico de uma função. 1. Introdução
MAT Poli Roteiro de Estudos sobre as Cônicas
 MAT25 - Poli - 2003 Roteiro de Estudos sobre as Cônicas Martha Salerno Monteiro Departamento de Matemática IME-USP Uma equação quadrática em duas variáveis é uma equação da forma a + by 2 + cxy + dx +
MAT25 - Poli - 2003 Roteiro de Estudos sobre as Cônicas Martha Salerno Monteiro Departamento de Matemática IME-USP Uma equação quadrática em duas variáveis é uma equação da forma a + by 2 + cxy + dx +
2 Igualdade e Operações com pares ordenados. 1 Conjunto R 2. 3 Vetores. 2.1 Igualdade. 1.2 Coordenadas Cartesianas no Plano
 1 Conjunto R 1.1 Definição VETORES NO PLANO Representamos por R o conjunto de todos os pares ordenados de números reais, ou seja: R = {(x, y) x R y R} 1. Coordenadas Cartesianas no Plano Em um plano α,
1 Conjunto R 1.1 Definição VETORES NO PLANO Representamos por R o conjunto de todos os pares ordenados de números reais, ou seja: R = {(x, y) x R y R} 1. Coordenadas Cartesianas no Plano Em um plano α,
Módulo de Geometria Anaĺıtica Parte 2. Circunferência. Professores Tiago Miranda e Cleber Assis
 Módulo de Geometria Anaĺıtica Parte Circunferência a série E.M. Professores Tiago Miranda e Cleber Assis Geometria Analítica Parte Circunferência 1 Exercícios Introdutórios Exercício 1. Em cada item abaixo,
Módulo de Geometria Anaĺıtica Parte Circunferência a série E.M. Professores Tiago Miranda e Cleber Assis Geometria Analítica Parte Circunferência 1 Exercícios Introdutórios Exercício 1. Em cada item abaixo,
Geometria Analítica - Sistemas de Coordenadas no Plano
 Geometria Analítica - Sistemas de Coordenadas no Plano Cleide Martins DMat - UFPE Turmas E1 e E3 Cleide Martins (DMat - UFPE) Retas e Elipses Turmas E1 e E3 1 / 1 Para denir um sistema de coordenadas no
Geometria Analítica - Sistemas de Coordenadas no Plano Cleide Martins DMat - UFPE Turmas E1 e E3 Cleide Martins (DMat - UFPE) Retas e Elipses Turmas E1 e E3 1 / 1 Para denir um sistema de coordenadas no
