UNIVERSIDADE FEDERAL DE PERNAMBUCO
|
|
|
- Antônia Gomes Pereira
- 7 Há anos
- Visualizações:
Transcrição
1 CÁLCULO L1 NOTAS DA DÉCIMA PRIMEIRA AULA UNIVERSIDADE FEDERAL DE PERNAMBUCO Resumo. Nesta aula, apresentaremos o Teorema do Valor Médio e algumas de suas conseqüências como: determinar os intervalos de crescimento e decrescimento de uma função; e estabelecer que a reta tangente é a que melhor aproxima uma curva no entorno do ponto de tangência. 1. O Teorema do Valor Médio (TVM) Utilizaremos o próximo resultado, que é conhecido como o Teorema de Rolle, para estabelecer o TVM. Teorema 1. Seja f uma função que assume o mesmo valor nos extremos do intervalo [a, b]. Se f(x) é contínua para todo X em [a, b] e possui derivada para todo X em (a, b), então existe c em (a, b) tal que f (c) = 0. Y f(a) = f(b) Y = f(x) a c b X Vamos estabeler o Teorema de Rolle veja a ilustração anterior. Se f(x) é constante no intervalo [a, b], então f (X) = 0 para todo X em (a, b). Portanto, neste caso, podemos tomar para c qualquer valor neste intevalo. Vamos assumir que f(x) não é constante no intervalo [a, b]. Como f(a) = f(b), o máximo ou o mínimo absoluto de f(x) no intervalo [a, b] ocorre em seu interior, digamos em X = c. Conseqüentemente será um máximo ou um mínimo local. Como, por hipótese, f (X) existe para todo X no interior do intervalo (a, b), temos que f (c) = 0 e o teorema segue. Agora enunciaremos o TVM que tem como caso particular o Teorema de Rolle. Teorema. Se f(x) é contínua para todo X em [a, b] e possui derivada para todo X em (a, b), então existe c em (a, b) tal que (1) f (c) = Note que o valor que está na direta da identidade (1) é o coeficiente angular da reta r que passa pelos pontos A e B de coordenadas (a, f(a)) e (b, f(b)) respectivamente que pertencem ao gráfico de f. Portanto, o TVM garante a existência de um ponto P no Estas notas foram escritas pelo professor da disciplina, Manoel Lemos. 1
2 UNIVERSIDADE FEDERAL DE PERNAMBUCO gráfico de f, entre A e B, cuja reta tangente t em P é paralela a r. Na figura segunte, o gráfico de f e a reta t têm traçados grossos e a reta r fino. Y P t f(a) A Y = f(x) f(b) r B a c b X Agora demonstraremos o TVM. A reta r é o gráfico da seguinte função ( ) r(x) = f(a) + (X a) Como r(a) = f(a) e r(b) = f(b), a função contínua no intervalo [a, b] dada por ( ) g(x) = f(x) r(x) = f(x) f(a) (X a) satisfaz g(a) = g(b) = 0. Como g (X) = f (X) existe para todo X em (a,b), podemos aplicar o Teorema de Role para g(x) neste intervalo. Conseqüentemente existe c em (a, b) tal que Isto é, Portanto, o TVM segue. 0 = g (c) = f (c) f (c) = A partir do TVM podemos concluir facilmente que o seguinte fato, utilizado anteriormente e justificado por um argumento baseado em uma interpretação oriunda da física, é válido: Se f (X) = 0 para todo X pertencente a um intervalo I, então f(x) é constante em I. Pelo TVM, para diferentes elementos a e b em I, existe c em (a, b) tal que f (c) = Como c está em I, temos que f (c) = 0 e daí f(a) = f(b). Isto é, f(x) é constante em I.. Crescimento e decrescimento O sinal da derivada de uma função é utilizado para determinar os intervalos para os quais esta função é crescente ou decrescente. Uma função f é dita crescente no intervalo I quando, para todos a e b em I tais que a < b, temos que f(a) < f(b). Uma função f é dita decrescente no intervalo I quando, para todos a e b em I tais que a < b, temos que f(a) > f(b).
3 MANOEL LEMOS 3 Agora apresentamos uma regra que, quando satisfeita, garante que a função é crescente ou decrescente em um dado intervalo. Regra 3. Se f(x) é uma função contínua no intervalo I, então: (i) f(x) é crescente em I quando f (X) > 0, para todo X no interior do intervalo I. (ii) f(x) é decrescente em I quando f (X) < 0, para todo X no interior do intervalo I. Vamos estabelecer a primeira parte desta regra, já que a segunda é verificada de maneira análoga. Escolha a e b em I tais que a < b. Necessitamos mostrar que f(a) < f(b) e, portanto, f(x) é crescente. Pelo TVM aplicado para f(x) e o intervalo [a, b], existe c em (a, b) tal que f (c) = Esta identidade pode ser reescrita como f (c)() = Como c está no interior do intervalo I, por hipótese, f (c) é positivo. Como também é positivo e o produto de dois números positivos é positivo, temos que é positivo. Isto é, f(a) < f(b). Conseqüentemente f(x) é crescente em I. Exemplo 4. Considere a função f(x), definida para todo número real X tal que X 1, que é dada pela expressão f(x) = X + 3 X 1 Estude o crescimento de f. Determinaremos as regiões de crescimento e decrescimento de f(x) a partir da sua derivada primeira f (X) = X(X 1) (X + 3) (X 1) = X X 3 (X 1) = (X + 1)(X 3) (X 1) Note que o denominador de f (X), para X 1, é sempre positivo. Portanto, o sinal de f (X) é igual ao sinal de (X + 1)(X 3), pois o quociente de dois números com o mesmo sinal é positivio e com sinais diferentes é negativo. Mas uma função quadrática com concavidade voltada para cima é negativa entre as raízes e positiva fora das raízes. Como, neste caso, as raízes são 1 e 3, o sinal de f (X) é sinal de f (X) Portanto, f(x) é crescente nos intervalos (, 1] e [3, + ). f(x) é decrescente nos intervalos [ 1, 1) e (1, 3]. Note que, pela Regra 3, não podemos garantir que a função f(x) é decrescente no intervalo [ 1, 3] porque f(x) não está definida para X = 1. (Na verdade, f(x) não é decrescente neste intervalo porque lim X 1 + f(x) = + e lim X 1 f(x) =.) Exemplo 5. Determine os intervalos de crescimento e decrescimento da função f dada por f(x) = X 4 + 4X 3 8X Ache todos os pontos de máximos e mínimos locais de f.
4 4 UNIVERSIDADE FEDERAL DE PERNAMBUCO Para fazer a análise do crescimento de f necessitamos estudar o sinal de f. Temos que f (X) = 4X 3 + 1X 16X = 4X(X + 3X 4) = 4(X + 4)X(X 1) Note que o sinal de f (X) coincide com o sinal de f (X) 4 = (X + 4)X(X 1) porque o produto de 4, que é positivo, por qualquer outro número preserva o seu sinal, isto é, o produto de um número positivo por um positivo é positivo e por um negativo é negativo. Mas (X + 4)X(X 1) é o produto de X + 4, X e X 1. A expressão X a é positiva quando a < X e negativa quando X < a. Apresentamos esta informação para cada caso específico nas três primeiras linhas do próximo quadro. A justificativa para a quarta linha vem a seguir. Observe que: Note que: sinal de X 1 sinal de X sinal de X + 4 sinal de f (X) 4 Quando X > 1, temos que X 1, X e X + 4 são todos positivos. O produto de três números positivos é positivo. Portanto f (X) > 0 para todo X > 1. Logo f(x) é crescente no intervalo [1, + ). Quando 0 < X < 1, temos que X e X + 4 são positivos e X 1 é negativo. O produto de dois números positivos por um negativo é negativo. Portanto f (X) < 0 para todo 0 < X < 1. Logo f(x) é decrescente no intervalo [0, 1]. Quando 4 < X < 0, temos que X + 4 é positivo e X e X 1 são negativos. O produto de dois números negativos por um positivo é positivo. Portanto f (X) > 0 para todo 4 < X < 0. Logo f(x) é decrescente no intervalo [ 4, 0]. Quando X < 4, temos que X 1, X e X + 4 são todos negativos. O produto de três números negativos é negativo. Portanto f (X) < 0 para todo X < 4. Logo f(x) é decrescente no intervalo (, 4]. X = 1 é um ponto de mínimo local para f(x) porque, em torno de X = 1, f(x) decresce até chegar em X = 1 e a partir deste valor cresce. X = 0 é um ponto de máximo local para f(x) porque, em torno de X = 0, f(x) cresce até chegar em X = 0 e a partir deste valor decresce. X = 4 é um ponto de mínimo local para f(x) porque, em torno de X = 4, f(x) decresce até chegar em X = 4 e a partir deste valor cresce. Exemplo 6. Mostre que a função f(x) = X sen X é crescente nos reais. Vamos analisar o sinal da derivada de f(x). Como f (X) = 1 cos X a função f(x) é crescente no intervalo [kπ, (k + 1)π], para todo k inteiro, porque f (X) > 0 para todo X no intervalo (kπ, (k + 1)π). Logo f(x) é crescente nos reais.
5 MANOEL LEMOS 5 Exemplo 7. Para comercializar o seu produto, uma fábrica de conservas deseja confeccionar uma embalagem de latão, na forma de um cilindro circular reto, com volume V. Qual deve ser as dimensões desta embalagem de forma que o material utilizado na sua produção seja mínimo? Sejam R e H o raio da base e a altura respectivamente da embalagem a ser produzida. Como esta embalagem tem volume V e forma de um cilindro circular reto, temos que V = πr H Retirando o valor de H desta expressão, obtemos () H = V πr Para minimizar o material utilizado, necessitamos minimizar a área total da embalagem. Isto é, temos de achar o mínimo de A = πrh + πr Ao substituirmos () nesta identidade, obtemos que ( ) V (3) A(R) = πr + πr = V πr R + πr (Escrevemos A(R) em vez de A para enfatizar o fato de a área A é apenas uma função de R lembre-se que V é uma constante.) Note que R pode assumir qualquer valor no intervalo (0, + ). Em outras palavras, desejamos encontra o mínimo absoluto de A(R) no intervalor (0, + ). Não temos um resultado que garanta a existência de tal mínimo como temos para o caso de um intervalo fechado. Vamos analisar o crescimento desta função. Temos que A (R) = V R + 4πR = (πr3 V ) R Para determinar os pontos críticos de A(R), temos de solucionar a equação A (R) = (πr3 V ) R = 0 Logo o numerador da fração é nulo, isto é, πr 3 V = 0 ou πr 3 = V Dividindo a identidade da direita por π e retiando a raiz cúbica, obtemos o valor de R V (4) R = 3 π que é o único ponto crítico de A(R). Observe que Quando R > 3 V, o numerador de π A (R) é positivo e conseqüentemente A (R) é positivo porque [ seu ) denominador é sempre positivo. Isto é, A(R) é crescente no 3 V intervalo, + π Quando R < 3 V, o numerador de π A (R) é negativo e conseqüentemente A (R) é negativo porque seu denominador é sempre positivo. Isto é, A(R) é decrescente no intervalo (0, 3 V π ]
6 6 UNIVERSIDADE FEDERAL DE PERNAMBUCO Conseqüentemente R = 3 V é um ponto de mínimo absoluto para A(R). Quando R π assume este valor, por (), temos que (5) H = 3 4V π Logo as dimensões da embalagem procurada são dadas por (4) e (5). Em particular, no mínimo, H = R, ou seja, a altura do cilindro é igual ao diâmetro da base. Exercício 8. Para cada uma das funções a seguir, cujo domínio de definição dever ser o maior possível, determine: (i) Este domínio. (ii) Seus intervalos de crescimento e decrescimento. (iii) Caso existam, pontos de máximo ou mínimo local. (iv) Caso existam, valor de máximo absoluto e valor de mínimo absoluto. a(x) = X 4 18X + 43 b(x) = X X + 1 X c(x) = (X + 1) ( ) + sen X d(x) = ln 3 + sen X e(x) = X e X Exercício 9. Determine as dimensões do cone circular reto circunscrito a uma esfera de raio R que possui área lateral mínima. Exercício 10. Determine as dimensões do cone circular reto circunscrito a uma esfera de raio R que possui volume mínimo. B α A P α B A
7 MANOEL LEMOS 7 Exercício 11. Na figura anterior dois meios homogênios são separados por um plano Π. Os pontos A e B estão localizados em meios diferentes. Assuma que a velocidade da luz no meio que contém o ponto A é V A e no que contém B é V B. Um raio de luz que vai de A até B passa por algum ponto P em Π. Sabendo que a luz percorre a trajetória que minimiza o tempo gasto para ir de A até B, mostre que V B cos α A = V A cos α B na qual α A e α B representam os ângulos entre Π e os segmentos AP e P B respectivamente. Exercício 1. Deseja-se fazer uma calha a partir de uma folha de latão de comprimento c e largura l curvando-a de forma que coincida com parte da superfície de um cilindro circular reto de comprimento c e raio da base r. Determine o valor de r para o qual a capaciadade da calha seja máxima. 3. A reta que melhor aproxima o gráfico de uma função Nesta parte da aula, iremos responder a seguinte pergunta sobre o gráfico de uma função f: de todas as retas que passam pelo ponto de coordenadas (a, f(a)), qual é a que melhor aproxima o gráfico f na vizinhança deste ponto? Mostraremos que, quando existir, é a reta tangente ao gráfico de f neste ponto É a reta tangente. Vamos assumir que o gráfico de f possua reta tangente no ponto (a, f(a)), ou seja, que f (a) existe. Uma reta com coeficiente angular m que passa pelo ponto (a, f(a)) é o gráfico da seguinte função: r(x) = f(a) + m(x a) Estamos interessados na distância do gráfico de f para o de r. Mediremos esta distância através da dirença entre as ordenadas dos pontos nestes gráficos possuindo a mesma abscissa. Isto é, consideraremos a seguinte função (6) d(x) = f(x) r(x) = f(x) f(a) m(x a) Como estamos interessados nesta diferença apenas para valores de X próximos de a, vamos comparar esta dirença com a distância de X até a, ou seja, com X a. Dividindo d(x) por X a obtemos (7) d(x) X a = f(x) f(a) X a m Quando X a, na qual o símbolo tem o significado de estar proximo, f(x) f(a) f (a) X a e conseqüentemente, por (7), temos que (8) d(x) X a f (a) m que é muito pequeno quando m conincide com f (a) apenas. Isto é, quando o gráfico de r é a reta tangente ao gráfico de f no ponto (a, f(a)). Podemos refinar este argumento para mostrar que (9) d(x) K X a para K = f (a) m quando X a. Note que K 0 quando o gráfico de r(x) não é a reta tangente ao gráfico de f(x) no ponto com coordenadas (a, f(a)).
8 8 UNIVERSIDADE FEDERAL DE PERNAMBUCO 3.. Estimando melhor a aproximação. Agora assuma que f (X) exista para todo X pertencente a um intervalo aberto I que contém a. Mostraremos que, para todo X em I, existe c(x) tal que c(x) está entre a e X tal que (10) f(x) = f(a) + f (a)(x a) + f (c(x)) (X a) Neste caso d(x) = f(x) f(a) f (a)(x a) = f (c(x)) (X a) e daí d(x) (11) X a = f (c(x)) X a Note que (1) nos diz quão próximo de 0 fica o quociente d(x) X a no caso em que m = f (a) compare com (8). Caso f (X) seja limitado por L no intervalo I, temos que (1) d(x) L X a Compare esta desigualdade com (9). Vamos mostrar que (10) vale para X = b que manteremos fixo. Considera a função (13) h(x) = f(x) f(a) f (a)(x a) λ (X a) Note que h(a) = 0. Escolha λ tal que h(b) = 0. Pelo TVM, existe s tal que h (s) = 0, com s entre a e b, porque h(a) = h(b) = 0. Como h (X) = f (X) f (a) λ(x a) temos que h (a) = 0. Pelo TVM, existe c entre a e s tal que h (c) = 0 porque h (a) = h (s) = 0. Como h (X) = f (X) λ, temos que λ = f (c). Substituindo este valor em (13), obtemos que (14) h(x) = f(x) f(a) f (a)(x a) f (c) (X a) Como, por hipótese, h(b) = 0, temos que (15) f(b) = f(a) + f (a)() + f (c) () Como c depende de b, enfatizamos esta dependência escrevendo-o como c(b). Isto é, (15) é reescrita como (16) f(b) = f(a) + f (a)() + f (c(b)) () que coincide com (10) pois b pode ser qualquer valor no intervalo I. 4. Respostas dos exercícios 8. (i) O domínio de todas estas funções é R exeto c(x) que não está definida apenas para X = 1 (ii) a(x) é crescente nos intervalos [ 3, 0] e [3, + ) e decrescente nos intervalos (, 3] e [0, 3]; b(x) é crescente no intervalo [ 1, 1] e decrescente nos intervalos (, 1] e [1, + ); c(x) é crescente no intervalo ( 1, 1] e decrescente nos intervalos (, 1) e [1, + ); para todo k inteiro, d(x) é crescente nos intervalos [ 3π + kπ, 5π + kπ] e decrescente nos intervalos [ π + kπ, 3π + kπ] ; e(x) é crescente no intervalo [0, ] e decrescente nos intervalos (, 0] e [, + ) (iii) para a(x): X = 3
9 MANOEL LEMOS 9 e X = 3 pontos de mínimos locais e X = 0 ponto de máximo local; para b(x): X = 1 ponto de mínimo local e X = 1 ponto de máximo local; para c(x): X = 1 ponto de máximo local; para d(x): para todo k inteiro, X = 3π + kπ ponto de mínimo local e X = π + kπ ponto de máximo local; para e(x): X = 0 ponto de mínimo local e X = ponto de máximo local (iv) a(x) não tem máximo ou mínimo absoluto; para b(x): X = 1 ponto de mínimo absoluto e X = 1 ponto de máximo absoluto; para c(x): X = 1 ponto de máximo absoluto e não tem ponto de mínimo absoluto; para d(x): para todo k inteiro, X = 3π + kπ ponto de mínimo absoluto e X = π + kπ ponto de máximo absoluto; para e(x): X = 0 ponto de mínimo absoluto e não possui ponto de máximo absoluto 9. A altura do cone é igual a 4R 10. A altura do cone é igual a 4R 1. l (isto 3 3 π é, uma seção transversal da calha será igual a um semi-círculo) Conteúdo da décima primeira aula da disciplina Cálculo L1, oferecida para os cursos de licenciatura em Física, Matemática e Química e o bacharelado em Química Idustrial, no segundo semestre de 008 na Universidade Federal de Pernambuco, tendo como professor Manoel Lemos
UNIVERSIDADE FEDERAL DE PERNAMBUCO. Resumo. Nesta aula, discutiremos a noção de continuidade que, juntamente com a diferenciação,
 CÁLCULO L1 NOTAS DA DÉCIMA AULA UNIVERSIDADE FEDERAL DE PERNAMBUCO Resumo. Nesta aula, discutiremos a noção de continuidade que, juntamente com a diferenciação, possibilitarão a solução de problemas de
CÁLCULO L1 NOTAS DA DÉCIMA AULA UNIVERSIDADE FEDERAL DE PERNAMBUCO Resumo. Nesta aula, discutiremos a noção de continuidade que, juntamente com a diferenciação, possibilitarão a solução de problemas de
UNIVERSIDADE FEDERAL DE PERNAMBUCO. Resumo. Nesta aula, veremos que o sinal da derivada segunda de uma função dá informações
 CÁLCULO L NOTAS DA DÉCIMA SEGUNDA AULA UNIVERSIDADE FEDERAL DE PERNAMBUCO Resumo. Nesta aula, veremos que o sinal da derivada segunda de uma função dá informações sobre a concavidade do gráfico desta função.
CÁLCULO L NOTAS DA DÉCIMA SEGUNDA AULA UNIVERSIDADE FEDERAL DE PERNAMBUCO Resumo. Nesta aula, veremos que o sinal da derivada segunda de uma função dá informações sobre a concavidade do gráfico desta função.
1. As funções tangente e secante As expressões para as funções tangente e secante são
 CÁLCULO L1 NOTAS DA SETA AULA UNIVERSIDADE FEDERAL DE PERNAMBUCO Resumo. Nesta aula definiremos as demais funções trigonométricas, que são obtidas a partir das funções seno e cosseno, e determinaremos
CÁLCULO L1 NOTAS DA SETA AULA UNIVERSIDADE FEDERAL DE PERNAMBUCO Resumo. Nesta aula definiremos as demais funções trigonométricas, que são obtidas a partir das funções seno e cosseno, e determinaremos
UNIVERSIDADE FEDERAL DE PERNAMBUCO
 CÁLCULO L1 NOTAS DA QUINTA AULA UNIVERSIDADE FEDERAL DE PERNAMBUCO Resumo. Iniciamos a aula definindo as funções trigonométricas e estabelecendo algumas de suas propriedades básicas. A seguir, calcularemos
CÁLCULO L1 NOTAS DA QUINTA AULA UNIVERSIDADE FEDERAL DE PERNAMBUCO Resumo. Iniciamos a aula definindo as funções trigonométricas e estabelecendo algumas de suas propriedades básicas. A seguir, calcularemos
UNIVERSIDADE FEDERAL DE PERNAMBUCO
 CÁLCULO L1 NOTAS DA PRIMEIRA AULA UNIVERSIDADE FEDERAL DE PERNAMBUCO Resumo. Nesta aula discutiremos como obter as equações das retas tangentes a uma curva planar que é o gráfico de uma função. 1. Introdução
CÁLCULO L1 NOTAS DA PRIMEIRA AULA UNIVERSIDADE FEDERAL DE PERNAMBUCO Resumo. Nesta aula discutiremos como obter as equações das retas tangentes a uma curva planar que é o gráfico de uma função. 1. Introdução
UNIVERSIDADE FEDERAL DE PERNAMBUCO
 CÁLCULO L NOTAS DA NONA AULA UNIVERSIDADE FEDERAL DE PERNAMBUCO Resumo. Nesta aula, apresentaremos as funções logaritmo e exponencial e calcularemos as suas derivadas. Também estabeleceremos algumas propriedades
CÁLCULO L NOTAS DA NONA AULA UNIVERSIDADE FEDERAL DE PERNAMBUCO Resumo. Nesta aula, apresentaremos as funções logaritmo e exponencial e calcularemos as suas derivadas. Também estabeleceremos algumas propriedades
UNIVERSIDADE FEDERAL DE PERNAMBUCO
 CÁLCULO L1 NOTAS DA TERCEIRA AULA UNIVERSIDADE FEDERAL DE PERNAMBUCO Resumo. Nesta aula introduziremos o conceito de derivada e a definição de uma reta tangente ao gráfico de uma função. Também apresentaremos
CÁLCULO L1 NOTAS DA TERCEIRA AULA UNIVERSIDADE FEDERAL DE PERNAMBUCO Resumo. Nesta aula introduziremos o conceito de derivada e a definição de uma reta tangente ao gráfico de uma função. Também apresentaremos
Aula 22 O teste da derivada segunda para extremos relativos.
 O teste da derivada segunda para extremos relativos. MÓDULO 2 - AULA 22 Aula 22 O teste da derivada segunda para extremos relativos. Objetivo: Utilizar a derivada segunda para determinar pontos de máximo
O teste da derivada segunda para extremos relativos. MÓDULO 2 - AULA 22 Aula 22 O teste da derivada segunda para extremos relativos. Objetivo: Utilizar a derivada segunda para determinar pontos de máximo
UNIVERSIDADE FEDERAL DE PERNAMBUCO
 CÁLCULO L NOTAS DA DÉCIMA TERCEIRA AULA UNIVERSIDADE FEDERAL DE PERNAMBUCO Resumo. Nesta aula, apresentaremos a Regra de L Hôpital, que será utilizada para solucionar indeterminações de ites de qualquer
CÁLCULO L NOTAS DA DÉCIMA TERCEIRA AULA UNIVERSIDADE FEDERAL DE PERNAMBUCO Resumo. Nesta aula, apresentaremos a Regra de L Hôpital, que será utilizada para solucionar indeterminações de ites de qualquer
Aula 25. Alexandre Nolasco de Carvalho Universidade de São Paulo São Carlos SP, Brazil
 Assíntotas, Esboço de Gráfico e Aplicações Aula 25 Alexandre Nolasco de Carvalho Universidade de São Paulo São Carlos SP, Brazil 09 de Maio de 2014 Primeiro Semestre de 2014 Turma 2014106 - Engenharia
Assíntotas, Esboço de Gráfico e Aplicações Aula 25 Alexandre Nolasco de Carvalho Universidade de São Paulo São Carlos SP, Brazil 09 de Maio de 2014 Primeiro Semestre de 2014 Turma 2014106 - Engenharia
Prova de Conhecimentos Específicos 1 a QUESTÃO: (2,0 pontos)
 Prova de Conhecimentos Específicos 1 a QUESTÃO: (,0 pontos) 5x Considere a função f(x)=. Determine, se existirem: x +7 (i) os pontos de descontinuidade de f; (ii) as assíntotas horizontais e verticais
Prova de Conhecimentos Específicos 1 a QUESTÃO: (,0 pontos) 5x Considere a função f(x)=. Determine, se existirem: x +7 (i) os pontos de descontinuidade de f; (ii) as assíntotas horizontais e verticais
CÁLCULO I. 1 Concavidade. Objetivos da Aula. Aula n o 16: Máximos e Mínimos - 2 a Parte
 CÁLCULO I Prof. Edilson Neri Júnior Prof. André Almeida Aula n o 16: Máximos e Mínimos - 2 a Parte Objetivos da Aula Denir e discutir a concavidade de uma função em um intervalo do domínio; Denir e calcular
CÁLCULO I Prof. Edilson Neri Júnior Prof. André Almeida Aula n o 16: Máximos e Mínimos - 2 a Parte Objetivos da Aula Denir e discutir a concavidade de uma função em um intervalo do domínio; Denir e calcular
UNIVERSIDADE FEDERAL DE PERNAMBUCO
 CÁLCULO L1 NOTAS DA VIGÉSIMA AULA UNIVERSIDADE FEDERAL DE PERNAMBUCO Resumo. Nesta aula, consideraremos mais uma técnica de integração, que é conhecida como substituição trigonométrica. Esta técnica pode
CÁLCULO L1 NOTAS DA VIGÉSIMA AULA UNIVERSIDADE FEDERAL DE PERNAMBUCO Resumo. Nesta aula, consideraremos mais uma técnica de integração, que é conhecida como substituição trigonométrica. Esta técnica pode
UNIVERSIDADE FEDERAL RURAL DE PERNAMBUCO UNIDADE ACADÊMICA DO CABO DE SANTO AGOSTINHO CÁLCULO DIFERENCIAL E INTEGRAL
 UNIVERSIDADE FEDERAL RURAL DE PERNAMBUCO UNIDADE ACADÊMICA DO CABO DE SANTO AGOSTINHO CÁLCULO DIFERENCIAL E INTEGRAL -. EXAME FINAL Nome Legível RG CPF Respostas sem justificativas não serão aceitas. Além
UNIVERSIDADE FEDERAL RURAL DE PERNAMBUCO UNIDADE ACADÊMICA DO CABO DE SANTO AGOSTINHO CÁLCULO DIFERENCIAL E INTEGRAL -. EXAME FINAL Nome Legível RG CPF Respostas sem justificativas não serão aceitas. Além
1. O raio de uma esfera está aumentando a uma taxa de 4 mm/s. Quão rápido o volume da esfera está aumentando quando o diâmetro for 80 mm?
 MAT 001 1 ō Sem. 016 IMC UNIFEI Lista 4: Aplicações da Derivação 1. O raio de uma esfera está aumentando a uma taxa de 4 mm/s. Quão rápido o volume da esfera está aumentando quando o diâmetro for 80 mm?.
MAT 001 1 ō Sem. 016 IMC UNIFEI Lista 4: Aplicações da Derivação 1. O raio de uma esfera está aumentando a uma taxa de 4 mm/s. Quão rápido o volume da esfera está aumentando quando o diâmetro for 80 mm?.
UNIVERSIDADE FEDERAL DE PERNAMBUCO. Resumo. Nesta aula, apresentaremos a noção de integral indefinidada. Também discutiremos
 CÁLCULO L NOTAS DA DÉCIMA OITAVA AULA UNIVERSIDADE FEDERAL DE PERNAMBUCO Resumo. Nesta aula, apresentaremos a noção de integral indefinidada. Também discutiremos a primeira técnica de integração: mudança
CÁLCULO L NOTAS DA DÉCIMA OITAVA AULA UNIVERSIDADE FEDERAL DE PERNAMBUCO Resumo. Nesta aula, apresentaremos a noção de integral indefinidada. Também discutiremos a primeira técnica de integração: mudança
MAT Cálculo I - POLI Gabarito da P2 - A
 MAT 45 - Cálculo I - POLI - 006 Gabarito da P - A Questão A) Calcule (.0) (a) lim ( cos() ) / (.0) (b) 0 ( ( π ) ) cos + e d (a) Tem-se, ( π/4, π/4) \ {0}: (cos ) / = ep( ln(cos )). Pondo f() =. ln(cos
MAT 45 - Cálculo I - POLI - 006 Gabarito da P - A Questão A) Calcule (.0) (a) lim ( cos() ) / (.0) (b) 0 ( ( π ) ) cos + e d (a) Tem-se, ( π/4, π/4) \ {0}: (cos ) / = ep( ln(cos )). Pondo f() =. ln(cos
MAT111 - Cálculo I - IME, BMAT & BMAP
 MAT - Cálculo I - IME, BMAT & BMAP - 04 a Lista de Exercícios -) Dois corredores iniciam uma corrida ao mesmo tempo e terminam empatados. Prove que em algum momento durante a corrida eles têm a mesma velocidade.
MAT - Cálculo I - IME, BMAT & BMAP - 04 a Lista de Exercícios -) Dois corredores iniciam uma corrida ao mesmo tempo e terminam empatados. Prove que em algum momento durante a corrida eles têm a mesma velocidade.
3 A Reta Tangente Definição: Seja y = f(x) uma curva definida no intervalo. curva y = f(x). A reta secante s é a reta que passa pelos pontos
 3 A Reta Tangente Definição: Seja y = f(x) uma curva definida no intervalo (a, b) Sejam P(p, f(p)) e Q(x, f(x)) dois pontos distintos da curva y = f(x). A reta secante s é a reta que passa pelos pontos
3 A Reta Tangente Definição: Seja y = f(x) uma curva definida no intervalo (a, b) Sejam P(p, f(p)) e Q(x, f(x)) dois pontos distintos da curva y = f(x). A reta secante s é a reta que passa pelos pontos
12. Diferenciação Logarítmica
 2. Diferenciação Logarítmica A diferenciação logarítmica é uma técnica útil para diferenciar funções compostas de potências, produtos e quocientes de funções. Esta técnica consiste em executar os seguintes
2. Diferenciação Logarítmica A diferenciação logarítmica é uma técnica útil para diferenciar funções compostas de potências, produtos e quocientes de funções. Esta técnica consiste em executar os seguintes
Aula 15. Derivadas Direcionais e Vetor Gradiente. Quando u = (1, 0) ou u = (0, 1), obtemos as derivadas parciais em relação a x ou y, respectivamente.
 Aula 15 Derivadas Direcionais e Vetor Gradiente Seja f(x, y) uma função de variáveis. Iremos usar a notação D u f(x 0, y 0 ) para: Derivada direcional de f no ponto (x 0, y 0 ), na direção do vetor unitário
Aula 15 Derivadas Direcionais e Vetor Gradiente Seja f(x, y) uma função de variáveis. Iremos usar a notação D u f(x 0, y 0 ) para: Derivada direcional de f no ponto (x 0, y 0 ), na direção do vetor unitário
Universidade Federal de Pelotas. Instituto de Física e Matemática Pró-reitoria de Ensino. Módulo de Limites. Aula 01. Projeto GAMA
 Universidade Federal de Pelotas Instituto de Física e Matemática Pró-reitoria de Ensino Atividades de Reforço em Cálculo Módulo de Limites Aula 0 208/ Projeto GAMA Grupo de Apoio em Matemática Ideia Intuitiva
Universidade Federal de Pelotas Instituto de Física e Matemática Pró-reitoria de Ensino Atividades de Reforço em Cálculo Módulo de Limites Aula 0 208/ Projeto GAMA Grupo de Apoio em Matemática Ideia Intuitiva
Instituto de Matemática - IM/UFRJ Cálculo I - MAC118 1 a Prova - Gabarito - 13/10/2016
 Instituto de Matemática - IM/UFRJ Cálculo I - MAC118 1 a Prova - Gabarito - 13/10/2016 Questão 1: (2 pontos) x (a) (0.4 ponto) Calcule o ite: 2 + 3 2. x 1 x 1 ( πx + 5 ) (b) (0.4 ponto) Calcule o ite:
Instituto de Matemática - IM/UFRJ Cálculo I - MAC118 1 a Prova - Gabarito - 13/10/2016 Questão 1: (2 pontos) x (a) (0.4 ponto) Calcule o ite: 2 + 3 2. x 1 x 1 ( πx + 5 ) (b) (0.4 ponto) Calcule o ite:
Prova Escrita de MATEMÁTICA A - 12o Ano a Fase
 Prova Escrita de MATEMÁTICA A - o Ano 0 - a Fase Proposta de resolução GRUPO I. Temos que P A B) P A) + P B) P A B) P A B) P A) + P B) P A B) Como A e B são independentes, então P A) P B) P A B), pelo
Prova Escrita de MATEMÁTICA A - o Ano 0 - a Fase Proposta de resolução GRUPO I. Temos que P A B) P A) + P B) P A B) P A B) P A) + P B) P A B) Como A e B são independentes, então P A) P B) P A B), pelo
MAT Cálculo Diferencial e Integral para Engenharia I
 MAT5 - Cálculo Diferencial e Integral para Engenharia I o Semestre de 0 - a Lista de Exercícios. Sejam f(x) = x + 5x 6 e g a função inversa de f. Admitindo que g e g são deriváveis, calcule g e g em termos
MAT5 - Cálculo Diferencial e Integral para Engenharia I o Semestre de 0 - a Lista de Exercícios. Sejam f(x) = x + 5x 6 e g a função inversa de f. Admitindo que g e g são deriváveis, calcule g e g em termos
MATEMÁTICA A - 11o Ano Funções - Derivada (extremos, monotonia e retas tangentes) Propostas de resolução
 MATEMÁTICA A - o Ano Funções - Derivada extremos, monotonia e retas tangentes) Propostas de resolução Exercícios de exames e testes intermédios. Temos que, pela definição de derivada num ponto, f ) fx)
MATEMÁTICA A - o Ano Funções - Derivada extremos, monotonia e retas tangentes) Propostas de resolução Exercícios de exames e testes intermédios. Temos que, pela definição de derivada num ponto, f ) fx)
Capítulo 3. Função afim. ANOTAÇÕES EM AULA Capítulo 3 Função afim 1.5 CONEXÕES COM A MATEMÁTICA
 Capítulo 3 Função afim 1.5 Função afim Uma função f: R R é função afim quando existem os números reais a e b tais que f(x) = ax + b para todo x R. Exemplos f(x) =, em que: a = e b = 6 g(x) = 7x, em que:
Capítulo 3 Função afim 1.5 Função afim Uma função f: R R é função afim quando existem os números reais a e b tais que f(x) = ax + b para todo x R. Exemplos f(x) =, em que: a = e b = 6 g(x) = 7x, em que:
A derivada da função inversa, o Teorema do Valor Médio e Máximos e Mínimos - Aula 18
 A derivada da função inversa, o Teorema do Valor Médio e - Aula 18 Alexandre Nolasco de Carvalho Universidade de São Paulo São Carlos SP, Brazil 10 de Abril de 2014 Primeiro Semestre de 2014 Turma 2014106
A derivada da função inversa, o Teorema do Valor Médio e - Aula 18 Alexandre Nolasco de Carvalho Universidade de São Paulo São Carlos SP, Brazil 10 de Abril de 2014 Primeiro Semestre de 2014 Turma 2014106
A integral definida Problema:
 A integral definida Seja y = f(x) uma função definida e limitada no intervalo [a, b], e tal que f(x) 0 p/ todo x [a, b]. Problema: Calcular (definir) a área, A,da região do plano limitada pela curva y
A integral definida Seja y = f(x) uma função definida e limitada no intervalo [a, b], e tal que f(x) 0 p/ todo x [a, b]. Problema: Calcular (definir) a área, A,da região do plano limitada pela curva y
Assinale as questões verdadeiras some os resultados obtidos e marque na Folha de Respostas:
 PROVA DE MATEMÁTICA - TURMAS DO O ANO DO ENSINO MÉDIO COLÉGIO ANCHIETA-BA - MAIO DE 0. ELABORAÇÃO: PROFESSORES OCTAMAR MARQUES E ADRIANO CARIBÉ. PROFESSORA MARIA ANTÔNIA C. GOUVEIA Assinale as questões
PROVA DE MATEMÁTICA - TURMAS DO O ANO DO ENSINO MÉDIO COLÉGIO ANCHIETA-BA - MAIO DE 0. ELABORAÇÃO: PROFESSORES OCTAMAR MARQUES E ADRIANO CARIBÉ. PROFESSORA MARIA ANTÔNIA C. GOUVEIA Assinale as questões
Universidade Federal de Viçosa Centro de Ciências Exatas Departamento de Matemática
 Universidade Federal de Viçosa Centro de Ciências Exatas Departamento de Matemática a Lista MAT 146 - Cálculo I 018/I DERIVADAS Para este tópico considera-se uma função f : D R R, definida num domínio
Universidade Federal de Viçosa Centro de Ciências Exatas Departamento de Matemática a Lista MAT 146 - Cálculo I 018/I DERIVADAS Para este tópico considera-se uma função f : D R R, definida num domínio
Índice. AULA 6 Integrais trigonométricas 3. AULA 7 Substituição trigonométrica 6. AULA 8 Frações parciais 8. AULA 9 Área entre curvas 11
 www.matematicaemexercicios.com Integrais (volume ) Índice AULA 6 Integrais trigonométricas 3 AULA 7 Substituição trigonométrica 6 AULA 8 Frações parciais 8 AULA 9 Área entre curvas AULA Volumes 3 www.matematicaemexercicios.com
www.matematicaemexercicios.com Integrais (volume ) Índice AULA 6 Integrais trigonométricas 3 AULA 7 Substituição trigonométrica 6 AULA 8 Frações parciais 8 AULA 9 Área entre curvas AULA Volumes 3 www.matematicaemexercicios.com
MAT Cálculo para Ciências Biológicas - Farmácia Prof. Gláucio Terra. 3 a Lista de Exercícios
 MAT0143 - Cálculo para Ciências Biológicas - Farmácia - 006 Prof. Gláucio Terra 3 a Lista de Eercícios 1-) Dois corredores iniciam uma corrida ao mesmo tempo e terminam empatados. Prove que em algum momento
MAT0143 - Cálculo para Ciências Biológicas - Farmácia - 006 Prof. Gláucio Terra 3 a Lista de Eercícios 1-) Dois corredores iniciam uma corrida ao mesmo tempo e terminam empatados. Prove que em algum momento
MAT146 - Cálculo I - Teorema do Valor Médio
 Alexandre Miranda Alves Anderson Tiago da Silva Edson José Teixeira Motivação Suponha que uma função real f, definida em um intervalo I, seja derivável em todo I. Sabemos que se f é uma função constante,
Alexandre Miranda Alves Anderson Tiago da Silva Edson José Teixeira Motivação Suponha que uma função real f, definida em um intervalo I, seja derivável em todo I. Sabemos que se f é uma função constante,
Índice. AULA 5 Derivação implícita 3. AULA 6 Aplicações de derivadas 4. AULA 7 Aplicações de derivadas 6. AULA 8 Esboço de gráficos 9
 www.matematicaemexercicios.com Derivadas Vol. 2 1 Índice AULA 5 Derivação implícita 3 AULA 6 Aplicações de derivadas 4 AULA 7 Aplicações de derivadas 6 AULA 8 Esboço de gráficos 9 www.matematicaemexercicios.com
www.matematicaemexercicios.com Derivadas Vol. 2 1 Índice AULA 5 Derivação implícita 3 AULA 6 Aplicações de derivadas 4 AULA 7 Aplicações de derivadas 6 AULA 8 Esboço de gráficos 9 www.matematicaemexercicios.com
Integração Volume. Aula 07 Matemática II Agronomia Prof. Danilene Donin Berticelli
 Integração Volume Aula 7 Matemática II Agronomia Prof. Danilene Donin Berticelli Volume de um sólido Na tentativa de encontra o volume de um sólido, nos deparamos com o mesmo tipo de problema que para
Integração Volume Aula 7 Matemática II Agronomia Prof. Danilene Donin Berticelli Volume de um sólido Na tentativa de encontra o volume de um sólido, nos deparamos com o mesmo tipo de problema que para
Exercício 1 Dê o valor, caso exista, que a função deveria assumir no ponto dado para. em p = 9
 Exercícios - Limite e Continuidade-1 Exercício 1 Dê o valor, caso exista, que a função deveria assumir no ponto dado para ser contínua: (a) f(x) = x2 16 x 4 (b) f(x) = x3 x x em p = 4 em p = 0 (c) f(x)
Exercícios - Limite e Continuidade-1 Exercício 1 Dê o valor, caso exista, que a função deveria assumir no ponto dado para ser contínua: (a) f(x) = x2 16 x 4 (b) f(x) = x3 x x em p = 4 em p = 0 (c) f(x)
Todos os exercícios sugeridos nesta apostila se referem ao volume 3. MATEMÁTICA III 1 ESTUDO DA CIRCUNFERÊNCIA
 DEFINIÇÃO... EQUAÇÃO REDUZIDA... EQUAÇÃO GERAL DA CIRCUNFERÊNCIA... 3 RECONHECIMENTO... 3 POSIÇÃO RELATIVA ENTRE PONTO E CIRCUNFERÊNCIA... 1 POSIÇÃO RELATIVA ENTRE RETA E CIRCUNFERÊNCIA... 17 PROBLEMAS
DEFINIÇÃO... EQUAÇÃO REDUZIDA... EQUAÇÃO GERAL DA CIRCUNFERÊNCIA... 3 RECONHECIMENTO... 3 POSIÇÃO RELATIVA ENTRE PONTO E CIRCUNFERÊNCIA... 1 POSIÇÃO RELATIVA ENTRE RETA E CIRCUNFERÊNCIA... 17 PROBLEMAS
Lista Mínima de Exercícios - Esboço de Gráfico/Máximos e
 Lista Mínima de Exercícios - Esboço de Gráfico/Máximos e Mínimos Exercício 1 Determine os intervalos de crescimento e de decrescimento, calcule todos os limites necessários e esboce o gráfico de f, onde
Lista Mínima de Exercícios - Esboço de Gráfico/Máximos e Mínimos Exercício 1 Determine os intervalos de crescimento e de decrescimento, calcule todos os limites necessários e esboce o gráfico de f, onde
Concluimos dai que o centro da circunferência é C = (6, 4) e o raio é
 QUESTÕES-AULA 17 1. A equação x 2 + y 2 12x + 8y + 0 = 0 representa uma circunferência de centro C = (a, b) e de raio R. Determinar o valor de a + b + R. Solução Completamos quadrados na expressão dada.
QUESTÕES-AULA 17 1. A equação x 2 + y 2 12x + 8y + 0 = 0 representa uma circunferência de centro C = (a, b) e de raio R. Determinar o valor de a + b + R. Solução Completamos quadrados na expressão dada.
Universidade Federal de Viçosa Centro de Ciências Exatas Departamento de Matemática
 Universidade Federal de Viçosa Centro de Ciências Exatas Departamento de Matemática 3 a Lista MAT 146 - Cálculo I 218/I APLICAÇÃO DE DERIVADAS: OTIMIZAÇÃO Otimização é outra aplicação de derivadas. Em
Universidade Federal de Viçosa Centro de Ciências Exatas Departamento de Matemática 3 a Lista MAT 146 - Cálculo I 218/I APLICAÇÃO DE DERIVADAS: OTIMIZAÇÃO Otimização é outra aplicação de derivadas. Em
INSTITUTO DE MATEMÁTICA E ESTATÍSTICA UNIVERSIDADE DE SÃO PAULO
 INSTITUTO DE MATEMÁTICA E ESTATÍSTICA UNIVERSIDADE DE SÃO PAULO MAT-2453 Cálculo Diferencial e Integral I Escola Politécnica) Segunda Lista de Eercícios - Professor: Equipe de Professores EXERCÍCIOS. Calcule
INSTITUTO DE MATEMÁTICA E ESTATÍSTICA UNIVERSIDADE DE SÃO PAULO MAT-2453 Cálculo Diferencial e Integral I Escola Politécnica) Segunda Lista de Eercícios - Professor: Equipe de Professores EXERCÍCIOS. Calcule
INSTITUTO DE MATEMÁTICA E ESTATÍSTICA UNIVERSIDADE DE SÃO PAULO
 INSTITUTO DE MATEMÁTICA E ESTATÍSTICA UNIVERSIDADE DE SÃO PAULO MAT-2453 Cálculo Diferencial e Integral I (Escola Politécnica) Segunda Lista de Eercícios - Professor: Equipe de Professores EXERCÍCIOS.
INSTITUTO DE MATEMÁTICA E ESTATÍSTICA UNIVERSIDADE DE SÃO PAULO MAT-2453 Cálculo Diferencial e Integral I (Escola Politécnica) Segunda Lista de Eercícios - Professor: Equipe de Professores EXERCÍCIOS.
Universidade Federal de Alagoas Instituto de Matemática Curso de Graduação em Matemática. Banco de Questões
 Universidade Federal de Alagoas Instituto de Matemática Curso de Graduação em Matemática Banco de Questões Cálculo 1 Maceió, Brasil 11 de Março de 2010 Sumário 1 2005 3 1.1 1 a Avaliação-21 de fevereiro
Universidade Federal de Alagoas Instituto de Matemática Curso de Graduação em Matemática Banco de Questões Cálculo 1 Maceió, Brasil 11 de Março de 2010 Sumário 1 2005 3 1.1 1 a Avaliação-21 de fevereiro
Instituto de Matemática - IM/UFRJ Cálculo Diferencial e Integral I - MAC238 Respostas da Prova de Final - 20/12/2013
 Página de 8 Instituto de Matemática - IM/UFRJ Cálculo Diferencial e Integral I - MAC38 Respostas da Prova de Final - 0//03 Questão : ( pontos) (a) Dado o gráfico da função f, esboce o gráfico da função
Página de 8 Instituto de Matemática - IM/UFRJ Cálculo Diferencial e Integral I - MAC38 Respostas da Prova de Final - 0//03 Questão : ( pontos) (a) Dado o gráfico da função f, esboce o gráfico da função
Prova 3 Matemática. N ọ DE INSCRIÇÃO:
 Prova QUESTÕES OBJETIIVAS N ọ DE ORDEM: NOME DO CANDIDATO: N ọ DE INSCRIÇÃO: IINSTRUÇÕES PARA A REALIIZAÇÃO DA PROVA. Confira os campos N ọ DE ORDEM, N ọ DE INSCRIÇÃO e NOME, conforme o que consta na etiqueta
Prova QUESTÕES OBJETIIVAS N ọ DE ORDEM: NOME DO CANDIDATO: N ọ DE INSCRIÇÃO: IINSTRUÇÕES PARA A REALIIZAÇÃO DA PROVA. Confira os campos N ọ DE ORDEM, N ọ DE INSCRIÇÃO e NOME, conforme o que consta na etiqueta
Prova 3 Matemática. N ọ DE INSCRIÇÃO:
 Prova QUESTÕES OBJETIIVAS N ọ DE ORDEM: NOME DO CANDIDATO: N ọ DE INSCRIÇÃO: IINSTRUÇÕES PARA A REALIIZAÇÃO DA PROVA. Confira os campos N ọ DE ORDEM, N ọ DE INSCRIÇÃO e NOME, conforme o que consta na etiqueta
Prova QUESTÕES OBJETIIVAS N ọ DE ORDEM: NOME DO CANDIDATO: N ọ DE INSCRIÇÃO: IINSTRUÇÕES PARA A REALIIZAÇÃO DA PROVA. Confira os campos N ọ DE ORDEM, N ọ DE INSCRIÇÃO e NOME, conforme o que consta na etiqueta
Prova 3 Matemática. N ọ DE INSCRIÇÃO:
 Prova QUESTÕES OBJETIIVAS N ọ DE ORDEM: NOME DO CANDIDATO: N ọ DE INSCRIÇÃO: IINSTRUÇÕES PARA A REALIIZAÇÃO DA PROVA. Confira os campos N ọ DE ORDEM, N ọ DE INSCRIÇÃO e NOME, conforme o que consta na etiqueta
Prova QUESTÕES OBJETIIVAS N ọ DE ORDEM: NOME DO CANDIDATO: N ọ DE INSCRIÇÃO: IINSTRUÇÕES PARA A REALIIZAÇÃO DA PROVA. Confira os campos N ọ DE ORDEM, N ọ DE INSCRIÇÃO e NOME, conforme o que consta na etiqueta
Prova 3 Matemática. N ọ DE INSCRIÇÃO:
 Prova QUESTÕES OBJETIIVAS N ọ DE ORDEM: NOME DO CANDIDATO: N ọ DE INSCRIÇÃO: IINSTRUÇÕES PARA A REALIIZAÇÃO DA PROVA. Confira os campos N ọ DE ORDEM, N ọ DE INSCRIÇÃO e NOME, conforme o que consta na etiqueta
Prova QUESTÕES OBJETIIVAS N ọ DE ORDEM: NOME DO CANDIDATO: N ọ DE INSCRIÇÃO: IINSTRUÇÕES PARA A REALIIZAÇÃO DA PROVA. Confira os campos N ọ DE ORDEM, N ọ DE INSCRIÇÃO e NOME, conforme o que consta na etiqueta
ENQ Gabarito MESTRADO PROFISSIONAL EM MATEMÁTICA EM REDE NACIONAL. (a) Sejam a, b, n Z com n > 0. Mostre que a + b a 2n b 2n.
 MESTRADO PROFISSIONAL EM MATEMÁTICA EM REDE NACIONAL ENQ 2018.2 Gabarito Questão 01 [ 1,25 ::: (a)=0,50; (b)=0,75 ] (a) Sejam a, b, n Z com n > 0. Mostre que a + b a 2n b 2n. (b) Para quais valores de
MESTRADO PROFISSIONAL EM MATEMÁTICA EM REDE NACIONAL ENQ 2018.2 Gabarito Questão 01 [ 1,25 ::: (a)=0,50; (b)=0,75 ] (a) Sejam a, b, n Z com n > 0. Mostre que a + b a 2n b 2n. (b) Para quais valores de
INSTITUTO DE MATEMÁTICA E ESTATÍSTICA UNIVERSIDADE DE SÃO PAULO
 INSTITUTO DE MATEMÁTICA E ESTATÍSTICA UNIVERSIDADE DE SÃO PAULO MAT-0 Cálculo Diferencial e Integral I (Instituto de Física) Segunda Lista de Eercícios - Professor: Aleandre Lymberopoulos. Calcule a derivada
INSTITUTO DE MATEMÁTICA E ESTATÍSTICA UNIVERSIDADE DE SÃO PAULO MAT-0 Cálculo Diferencial e Integral I (Instituto de Física) Segunda Lista de Eercícios - Professor: Aleandre Lymberopoulos. Calcule a derivada
= 2 sen(x) (cos(x) (b) (7 pontos) Pelo item anterior, temos as k desigualdades. sen 2 (2x) sen(4x) ( 3/2) 3
 Problema (a) (3 pontos) Sendo f(x) = sen 2 (x) sen(2x), uma função π-periódica, temos que f (x) = 2 sen(x) cos(x) sen(2x) + sen 2 (x) 2 cos(2x) = 2 sen(x) (cos(x) sen(2x) + sen(x) cos(2x) ) = 2 sen(x)
Problema (a) (3 pontos) Sendo f(x) = sen 2 (x) sen(2x), uma função π-periódica, temos que f (x) = 2 sen(x) cos(x) sen(2x) + sen 2 (x) 2 cos(2x) = 2 sen(x) (cos(x) sen(2x) + sen(x) cos(2x) ) = 2 sen(x)
Prova Escrita de MATEMÁTICA A - 12o Ano a Fase
 Prova Escrita de MATEMÁTICA A - o Ano 05 - a Fase Proposta de resolução GRUPO I. Escolhendo os lugares das etremidades para os dois rapazes, eistem hipóteses correspondentes a uma troca entre os rapazes.
Prova Escrita de MATEMÁTICA A - o Ano 05 - a Fase Proposta de resolução GRUPO I. Escolhendo os lugares das etremidades para os dois rapazes, eistem hipóteses correspondentes a uma troca entre os rapazes.
MAT Poli Cônicas - Parte I
 MAT2454 - Poli - 2011 Cônicas - Parte I Uma equação quadrática em duas variáveis, x e y, é uma equação da forma ax 2 +by 2 +cxy +dx+ey +f = 0, em que pelo menos um doscoeficientes a, b oucénão nulo 1.
MAT2454 - Poli - 2011 Cônicas - Parte I Uma equação quadrática em duas variáveis, x e y, é uma equação da forma ax 2 +by 2 +cxy +dx+ey +f = 0, em que pelo menos um doscoeficientes a, b oucénão nulo 1.
Prova de Conhecimentos Específicos 1 a QUESTÃO: (2,0 pontos)
 Prova de Conhecimentos Específicos 1 a QUESTÃO: (,0 pontos) a) etermine números reais a 0, b, c, e d tais que o gráfico de f(x) ax + bx + cx + d tenha um ponto de inflexão em (1, ) e o coeficiente angular
Prova de Conhecimentos Específicos 1 a QUESTÃO: (,0 pontos) a) etermine números reais a 0, b, c, e d tais que o gráfico de f(x) ax + bx + cx + d tenha um ponto de inflexão em (1, ) e o coeficiente angular
Conjuntos Numéricos. I) Números Naturais N = { 0, 1, 2, 3,... }
 Conjuntos Numéricos I) Números Naturais N = { 0, 1, 2, 3,... } II) Números Inteiros Z = {..., -2, -1, 0, 1, 2,... } Todo número natural é inteiro, isto é, N é um subconjunto de Z III) Números Racionais
Conjuntos Numéricos I) Números Naturais N = { 0, 1, 2, 3,... } II) Números Inteiros Z = {..., -2, -1, 0, 1, 2,... } Todo número natural é inteiro, isto é, N é um subconjunto de Z III) Números Racionais
CÁLCULO I. 1 Funções Crescentes e Decrescentes
 CÁLCULO I Prof. Marcos Diniz Prof. André Almeida Prof. Edilson Neri Júnior Aula n o 17: Crescimento e Decrescimento de funções. Teste da Primeira Derivada. Objetivos da Aula Denir funções crescentes e
CÁLCULO I Prof. Marcos Diniz Prof. André Almeida Prof. Edilson Neri Júnior Aula n o 17: Crescimento e Decrescimento de funções. Teste da Primeira Derivada. Objetivos da Aula Denir funções crescentes e
6.1.2 Derivada de ordem superior e derivação implícita
 6.1. DERIVABILIDADE E DIFERENCIABILIDADE 111 6.1.2 Derivada de ordem superior e derivação implícita Observe que se f é derivável num subconjunto A de seu domínio D, obtemos então uma nova função g = f
6.1. DERIVABILIDADE E DIFERENCIABILIDADE 111 6.1.2 Derivada de ordem superior e derivação implícita Observe que se f é derivável num subconjunto A de seu domínio D, obtemos então uma nova função g = f
MAT146 - Cálculo I - FEA, Economia
 MAT46 - Cálculo I - FEA, Economia - 202 a Lista de Exercícios Limites de Funções. Calcule os seguintes limites, caso existam: 5 3x + 9 ) lim 2) lim x 3 x x 3 x + 3 x 2 + 0x 6 4) lim x 8 2x 2 4x 6 x 7)
MAT46 - Cálculo I - FEA, Economia - 202 a Lista de Exercícios Limites de Funções. Calcule os seguintes limites, caso existam: 5 3x + 9 ) lim 2) lim x 3 x x 3 x + 3 x 2 + 0x 6 4) lim x 8 2x 2 4x 6 x 7)
A Derivada. Derivadas Aula 16. Alexandre Nolasco de Carvalho Universidade de São Paulo São Carlos SP, Brazil
 Derivadas Aula 16 Alexandre Nolasco de Carvalho Universidade de São Paulo São Carlos SP, Brazil 04 de Abril de 2014 Primeiro Semestre de 2014 Turma 2014104 - Engenharia Mecânica A Derivada Seja x = f(t)
Derivadas Aula 16 Alexandre Nolasco de Carvalho Universidade de São Paulo São Carlos SP, Brazil 04 de Abril de 2014 Primeiro Semestre de 2014 Turma 2014104 - Engenharia Mecânica A Derivada Seja x = f(t)
CÁLCULO FUNÇÕES DE UMA E VÁRIAS VARIÁVEIS Pedro A. Morettin, Samuel Hazzan, Wilton de O. Bussab.
 Introdução Função é uma forma de estabelecer uma ligação entre dois conjuntos, sujeita a algumas condições. Antes, porém, será exposta uma forma de correspondência mais geral, chamada relação. Sejam dois
Introdução Função é uma forma de estabelecer uma ligação entre dois conjuntos, sujeita a algumas condições. Antes, porém, será exposta uma forma de correspondência mais geral, chamada relação. Sejam dois
ln(x + y) (x + y 1) < 1 (x + y 1)2 3. Determine o polinômio de Taylor de ordem 2 da função dada, em volta do ponto dado:
 ā Lista de MAT 454 - Cálculo II - a) POLINÔMIOS DE TAYLOR 1. Seja f(x, y) = ln (x + y). a) Determine o polinômio de Taylor de ordem um de f em torno de ( 1, 1 ). b) Mostre que para todo (x, y) IR com x
ā Lista de MAT 454 - Cálculo II - a) POLINÔMIOS DE TAYLOR 1. Seja f(x, y) = ln (x + y). a) Determine o polinômio de Taylor de ordem um de f em torno de ( 1, 1 ). b) Mostre que para todo (x, y) IR com x
A Segunda Derivada: Análise da Variação de Uma Função
 A Segunda Derivada: Análise da Variação de Uma Função Suponhamos que a função y = f() possua derivada em um segmento [a, b] do eio-. Os valores da derivada f () também dependem de, ou seja, a derivada
A Segunda Derivada: Análise da Variação de Uma Função Suponhamos que a função y = f() possua derivada em um segmento [a, b] do eio-. Os valores da derivada f () também dependem de, ou seja, a derivada
MAT111 - Cálculo Diferencial e Integral I - IO Prof. Gláucio Terra 2 a Lista de Exercícios
 MAT - Cálculo Diferencial e Integral I - IO - 05 Prof. Gláucio Terra a Lista de Exercícios - Sejam f(x = x 3 +5x 6 e g a função inversa de f. (a Calcule g (x e g (x (em função de x e de g(x; (b Calcule
MAT - Cálculo Diferencial e Integral I - IO - 05 Prof. Gláucio Terra a Lista de Exercícios - Sejam f(x = x 3 +5x 6 e g a função inversa de f. (a Calcule g (x e g (x (em função de x e de g(x; (b Calcule
2a. Lista de Exercícios
 UFPR - Universidade Federal do Paraná Departamento de Matemática Prof. José Carlos Eidam CM04 - Cálculo I - Turma C - 0/ a. Lista de Eercícios Teoremas do valor intermediário e do valor médio. Seja h()
UFPR - Universidade Federal do Paraná Departamento de Matemática Prof. José Carlos Eidam CM04 - Cálculo I - Turma C - 0/ a. Lista de Eercícios Teoremas do valor intermediário e do valor médio. Seja h()
MAT Cálculo Diferencial e Integral I
 MAT3110 - Cálculo Diferencial e Integral I Bacharelado em Matemática Aplicada e Computacional - IME/USP Lista de exercícios 4 23/04/2015 1. Encontre as equações das retas que passam pelo ponto (3, 2) e
MAT3110 - Cálculo Diferencial e Integral I Bacharelado em Matemática Aplicada e Computacional - IME/USP Lista de exercícios 4 23/04/2015 1. Encontre as equações das retas que passam pelo ponto (3, 2) e
x 2 + (x 2 5) 2, x 0, (1) 5 + y + y 2, y 5. (2) e é positiva em ( 2 3 , + ), logo x = 3
 Página 1 de 4 Instituto de Matemática - IM/UFRJ Cálculo Diferencial e Integral I - MAC 118 Gabarito segunda prova - Escola Politécnica / Escola de Química - 13/06/2017 Questão 1: (2 pontos) Determinar
Página 1 de 4 Instituto de Matemática - IM/UFRJ Cálculo Diferencial e Integral I - MAC 118 Gabarito segunda prova - Escola Politécnica / Escola de Química - 13/06/2017 Questão 1: (2 pontos) Determinar
Esboço de Gráfico - Exemplos e Regras de L Hospital Aula 23
 Esboço de Gráfico - s e Regras de L Hospital Aula 23 Alexandre Nolasco de Carvalho Universidade de São Paulo São Carlos SP, Brazil 06 de Maio de 2014 Primeiro Semestre de 2014 Turma 2014106 - Engenharia
Esboço de Gráfico - s e Regras de L Hospital Aula 23 Alexandre Nolasco de Carvalho Universidade de São Paulo São Carlos SP, Brazil 06 de Maio de 2014 Primeiro Semestre de 2014 Turma 2014106 - Engenharia
21 e 22. Superfícies Quádricas. Sumário
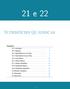 21 e 22 Superfícies uádricas Sumário 21.1 Introdução....................... 2 21.2 Elipsoide........................ 3 21.3 Hiperboloide de uma Folha.............. 4 21.4 Hiperboloide de duas folhas..............
21 e 22 Superfícies uádricas Sumário 21.1 Introdução....................... 2 21.2 Elipsoide........................ 3 21.3 Hiperboloide de uma Folha.............. 4 21.4 Hiperboloide de duas folhas..............
Prova Escrita de MATEMÁTICA A - 12o Ano a Fase
 Prova Escrita de MATEMÁTICA A - o Ano 7 - a Fase Proposta de resolução GRUPO I. Como a área do retângulo é igual a 5, designado por x o comprimento de um dos lados e por y o comprimento de um lado adjacente,
Prova Escrita de MATEMÁTICA A - o Ano 7 - a Fase Proposta de resolução GRUPO I. Como a área do retângulo é igual a 5, designado por x o comprimento de um dos lados e por y o comprimento de um lado adjacente,
Universidade Estadual de Montes Claros Departamento de Ciências Exatas Curso de Licenciatura em Matemática. Notas de Aulas de
 Universidade Estadual de Montes Claros Departamento de Ciências Exatas Curso de Licenciatura em Matemática Notas de Aulas de Cálculo Rosivaldo Antonio Gonçalves Notas de aulas que foram elaboradas para
Universidade Estadual de Montes Claros Departamento de Ciências Exatas Curso de Licenciatura em Matemática Notas de Aulas de Cálculo Rosivaldo Antonio Gonçalves Notas de aulas que foram elaboradas para
J. Delgado - K. Frensel - L. Crissaff Geometria Analítica e Cálculo Vetorial
 178 Capítulo 10 Equação da reta e do plano no espaço 1. Equações paramétricas da reta no espaço Sejam A e B dois pontos distintos no espaço e seja r a reta que os contém. Então, P r existe t R tal que
178 Capítulo 10 Equação da reta e do plano no espaço 1. Equações paramétricas da reta no espaço Sejam A e B dois pontos distintos no espaço e seja r a reta que os contém. Então, P r existe t R tal que
MAT Cálculo Diferencial e Integral para Engenharia I
 MAT453 - Cálculo Diferencial e Integral para Engenharia I 1 o Semestre de 011 - a Lista de Eercícios 1. Calcule a área da região compreendida entre os gráficos de f () = 3 + 1 e g() = + 1, com 1 1.. Desenhe
MAT453 - Cálculo Diferencial e Integral para Engenharia I 1 o Semestre de 011 - a Lista de Eercícios 1. Calcule a área da região compreendida entre os gráficos de f () = 3 + 1 e g() = + 1, com 1 1.. Desenhe
MAT146 - Cálculo I - Problemas de Otimização
 Alexandre Miranda Alves Anderson Tiago da Silva Edson José Teixeira Um problema de otimização é aquele onde se procura determinar os valores extremos de uma função, isto é, o maior ou o menor valor que
Alexandre Miranda Alves Anderson Tiago da Silva Edson José Teixeira Um problema de otimização é aquele onde se procura determinar os valores extremos de uma função, isto é, o maior ou o menor valor que
GABARITO S = { 1, 33; 0, 2} (VERDADEIRO) 08. 2x 5 = 8x x 2 9 x x = 3 e x = 3. x = 7 ± 3. x =
 88 0) x 0, 5 aplicando a prop. a n m m a n : 88 5 00 x 88 5 0 x 8 5 0 x 80 5 0 x 75 0 x 75x 0 x 0 75 x 5 multiplicando toda inequação por 0: multiplicando toda inequação por x: Porém, x 0, pois x é o denominador.
88 0) x 0, 5 aplicando a prop. a n m m a n : 88 5 00 x 88 5 0 x 8 5 0 x 80 5 0 x 75 0 x 75x 0 x 0 75 x 5 multiplicando toda inequação por 0: multiplicando toda inequação por x: Porém, x 0, pois x é o denominador.
Aulas n o 22: A Função Logaritmo Natural
 CÁLCULO I Aulas n o 22: A Função Logaritmo Natural Prof. Edilson Neri Júnior Prof. André Almeida 1 A Função Logaritmo Natural 2 Derivadas e Integral Propriedades dos Logaritmos 3 Gráfico Seja x > 0. Definimos
CÁLCULO I Aulas n o 22: A Função Logaritmo Natural Prof. Edilson Neri Júnior Prof. André Almeida 1 A Função Logaritmo Natural 2 Derivadas e Integral Propriedades dos Logaritmos 3 Gráfico Seja x > 0. Definimos
Prova Escrita de MATEMÁTICA A - 12o Ano a Fase
 Prova Escrita de MATEMÁTICA A - o Ano 06 - a Fase Proposta de resolução GRUPO I. Como P (A B) P (A B) P (B) P (A B) P (A B) P (B) vem que: P (A B) 6 0 60 0 Como P (A B) P (A) + P (B) P (A B), temos que:
Prova Escrita de MATEMÁTICA A - o Ano 06 - a Fase Proposta de resolução GRUPO I. Como P (A B) P (A B) P (B) P (A B) P (A B) P (B) vem que: P (A B) 6 0 60 0 Como P (A B) P (A) + P (B) P (A B), temos que:
Estudar mudança no valor de funções na vizinhança de pontos.
 Universidade Federal de Alagoas Faculdade de Arquitetura e Urbanismo Curso de Arquitetura e Urbanismo Disciplina: Fundamentos para a Análise Estrutural Código: AURB006 Turma: A Período Letivo: 007- Professor:
Universidade Federal de Alagoas Faculdade de Arquitetura e Urbanismo Curso de Arquitetura e Urbanismo Disciplina: Fundamentos para a Análise Estrutural Código: AURB006 Turma: A Período Letivo: 007- Professor:
Geometria Analítica II - Aula 4 82
 Geometria Analítica II - Aula 4 8 IM-UFF K. Frensel - J. Delgado Aula 5 Esferas Iniciaremos o nosso estudo sobre superfícies com a esfera, que já nos é familiar. A esfera S de centro no ponto A e raio
Geometria Analítica II - Aula 4 8 IM-UFF K. Frensel - J. Delgado Aula 5 Esferas Iniciaremos o nosso estudo sobre superfícies com a esfera, que já nos é familiar. A esfera S de centro no ponto A e raio
Funções de Uma Variável - 1 a Avaliação - Turma B3 31 de outubro de Prof. Armando Caputi
 Funções de Uma Variável - 1 a Avaliação - Turma B 1 de outubro de 017 - Prof. Armando Caputi 1 Determine o domínio da função f(x) = arctan x x + 1 (justifique) e a equação da reta tangente ao seu gráfico
Funções de Uma Variável - 1 a Avaliação - Turma B 1 de outubro de 017 - Prof. Armando Caputi 1 Determine o domínio da função f(x) = arctan x x + 1 (justifique) e a equação da reta tangente ao seu gráfico
CÁLCULO DIFERENCIAL E INTEGRAL I NOTAS DE AULAS Prof. Dr. Luiz Francisco da Cruz Departamento de Matemática UNESP/Bauru
 REGRA DE LHÔPITAL Teorema: Suponhamos que f (a) g(a) e que f (a) e g (a) eistam com g(a). Então: lim a f() g() f(a) g(a). in det er min ação. Forma mais avançada do Teorema de L Hospital: Suponhamos que
REGRA DE LHÔPITAL Teorema: Suponhamos que f (a) g(a) e que f (a) e g (a) eistam com g(a). Então: lim a f() g() f(a) g(a). in det er min ação. Forma mais avançada do Teorema de L Hospital: Suponhamos que
Exercícios de Cálculo - Prof. Ademir
 Exercícios de Cálculo - Prof. Ademir Funções, limites e continuidade. Considere f : IR IR definida por f(x) = x 4x + 3. (a) Faça um esboço do gráfico de f. (b) Determine os valores de x para os quais f(x)..
Exercícios de Cálculo - Prof. Ademir Funções, limites e continuidade. Considere f : IR IR definida por f(x) = x 4x + 3. (a) Faça um esboço do gráfico de f. (b) Determine os valores de x para os quais f(x)..
CPV O cursinho que mais aprova na fgv
 O cursinho que mais aprova na fgv FGV economia a Fase 0/dezembro/00 MATEMÁTICA 0 Na parte sombreada da figura, as extremidades dos segmentos de reta paralelos ao eixo y são pontos das representações gráficas
O cursinho que mais aprova na fgv FGV economia a Fase 0/dezembro/00 MATEMÁTICA 0 Na parte sombreada da figura, as extremidades dos segmentos de reta paralelos ao eixo y são pontos das representações gráficas
UNIVERSIDADE FEDERAL DA BAHIA INSTITUTO DE MATEMÁTICA DEPARTAMENTO DE MATEMÁTICA MAT A02 CÁLCULO A ª LISTA ( QUESTÕES DE PROVAS )
 UNIVERSIDADE FEDERAL DA BAHIA INSTITUTO DE MATEMÁTICA DEPARTAMENTO DE MATEMÁTICA MAT A0 CÁLCULO A 009 ª LISTA ( QUESTÕES DE PROVAS ) Regra da cadeia ( f ( g( h(( t( )))))) f ( g( h(( t( ))))) g ( h(( t(
UNIVERSIDADE FEDERAL DA BAHIA INSTITUTO DE MATEMÁTICA DEPARTAMENTO DE MATEMÁTICA MAT A0 CÁLCULO A 009 ª LISTA ( QUESTÕES DE PROVAS ) Regra da cadeia ( f ( g( h(( t( )))))) f ( g( h(( t( ))))) g ( h(( t(
Resolução dos Exercícios sobre Derivadas
 Resolução dos Eercícios sobre Derivadas Eercício Utilizando a idéia do eemplo anterior, encontre a reta tangente à curva = 0 e = y = nos pontos onde Vamos determinar a reta tangente à curva y = nos pontos
Resolução dos Eercícios sobre Derivadas Eercício Utilizando a idéia do eemplo anterior, encontre a reta tangente à curva = 0 e = y = nos pontos onde Vamos determinar a reta tangente à curva y = nos pontos
O problema proposto possui alguma solução? Se sim, quantas e quais são elas?
 PROVA PARA OS ALUNOS DE 3º ANO DO ENSINO MÉDIO 1) Considere o seguinte problema: Vitor ganhou R$ 3,20 de seu pai em moedas de 5 centavos, 10 centavos e 25 centavos. Se recebeu um total de 50 moedas, quantas
PROVA PARA OS ALUNOS DE 3º ANO DO ENSINO MÉDIO 1) Considere o seguinte problema: Vitor ganhou R$ 3,20 de seu pai em moedas de 5 centavos, 10 centavos e 25 centavos. Se recebeu um total de 50 moedas, quantas
Área de uma Superfície de Revolução
 UNIVERSIDADE DO ESTADO DE MATO GROSSO CAMPUS UNIVERSITÁRIO DE SINOP FACULDADE DE CIÊNCIAS EXATAS E TECNOLÓGICAS CURSO DE ENGENHARIA CIVIL DISCIPLINA: CÁLCULO DIFERENCIAL E INTEGRAL I Área de uma Superfície
UNIVERSIDADE DO ESTADO DE MATO GROSSO CAMPUS UNIVERSITÁRIO DE SINOP FACULDADE DE CIÊNCIAS EXATAS E TECNOLÓGICAS CURSO DE ENGENHARIA CIVIL DISCIPLINA: CÁLCULO DIFERENCIAL E INTEGRAL I Área de uma Superfície
ITA º DIA MATEMÁTICA BERNOULLI COLÉGIO E PRÉ-VESTIBULAR
 ITA - 2006 3º DIA MATEMÁTICA BERNOULLI COLÉGIO E PRÉ-VESTIBULAR Matemática Questão 01 Seja E um ponto externo a uma circunferência. Os segmentos e interceptam essa circunferência nos pontos B e A, e, C
ITA - 2006 3º DIA MATEMÁTICA BERNOULLI COLÉGIO E PRÉ-VESTIBULAR Matemática Questão 01 Seja E um ponto externo a uma circunferência. Os segmentos e interceptam essa circunferência nos pontos B e A, e, C
Prova Escrita de MATEMÁTICA A - 12o Ano a Fase
 Prova Escrita de MATEMÁTICA A - o Ano 00 - a Fase Proposta de resolução GRUPO I. Como só existem bolas azuis e roxas, e a probabilidade de extrair uma bola da caixa, e ela ser azul é igual a, então existem
Prova Escrita de MATEMÁTICA A - o Ano 00 - a Fase Proposta de resolução GRUPO I. Como só existem bolas azuis e roxas, e a probabilidade de extrair uma bola da caixa, e ela ser azul é igual a, então existem
Notas de Aulas 3 - Cônicas Prof Carlos A S Soares
 Notas de Aulas 3 - Cônicas Prof Carlos A S Soares 1 Parábolas 1.1 Conceito e Elementos Definição 1.1 Sejam l uma reta e F um ponto não pertencente a l. Chamamos parábola de diretriz l e foco F o conjunto
Notas de Aulas 3 - Cônicas Prof Carlos A S Soares 1 Parábolas 1.1 Conceito e Elementos Definição 1.1 Sejam l uma reta e F um ponto não pertencente a l. Chamamos parábola de diretriz l e foco F o conjunto
Material Teórico - Módulo de Função Exponencial. Primeiro Ano - Médio. Autor: Prof. Angelo Papa Neto Revisor: Prof. Antonio Caminha M.
 Material Teórico - Módulo de Função Exponencial Gráfico da Função Exponencial Primeiro Ano - Médio Autor: Prof. Angelo Papa Neto Revisor: Prof. Antonio Caminha M. Neto 0 de dezembro de 018 1 Funções convexas
Material Teórico - Módulo de Função Exponencial Gráfico da Função Exponencial Primeiro Ano - Médio Autor: Prof. Angelo Papa Neto Revisor: Prof. Antonio Caminha M. Neto 0 de dezembro de 018 1 Funções convexas
Capítulo 2. Retas no plano. 1. Retas verticais e não-verticais. Definição 1
 Capítulo 2 Retas no plano O objetivo desta aula é determinar a equação algébrica que representa uma reta no plano. Para isso, vamos analisar separadamente dois tipos de reta: reta vertical e reta não-vertical.
Capítulo 2 Retas no plano O objetivo desta aula é determinar a equação algébrica que representa uma reta no plano. Para isso, vamos analisar separadamente dois tipos de reta: reta vertical e reta não-vertical.
Resposta: f(g(x)) = x 5, onde g(x) é não negativa para todo x real. Assinale a alternativa cujo 5, 5 5, 5 3, 3. f(g(x) = x 5.
 1. (Espcex (Aman) 016) Considere as funções reais f e g, tais que f(x) = x + 4 e f(g(x)) = x 5, onde g(x) é não negativa para todo x real. Assinale a alternativa cujo conjunto contém todos os possíveis
1. (Espcex (Aman) 016) Considere as funções reais f e g, tais que f(x) = x + 4 e f(g(x)) = x 5, onde g(x) é não negativa para todo x real. Assinale a alternativa cujo conjunto contém todos os possíveis
INSTITUTO DE MATEMÁTICA E ESTATÍSTICA UNIVERSIDADE DE SÃO PAULO
 INSTITUTO DE MATEMÁTICA E ESTATÍSTICA UNIVERSIDADE DE SÃO PAULO MAT-2453 Cálculo Diferencial e Integral para Engenharia I Segunda Lista de Eercícios - Professor: Equipe da Disciplina. Calcule a derivada
INSTITUTO DE MATEMÁTICA E ESTATÍSTICA UNIVERSIDADE DE SÃO PAULO MAT-2453 Cálculo Diferencial e Integral para Engenharia I Segunda Lista de Eercícios - Professor: Equipe da Disciplina. Calcule a derivada
Distância entre duas retas. Regiões no plano
 Capítulo 4 Distância entre duas retas. Regiões no plano Nesta aula, veremos primeiro como podemos determinar a distância entre duas retas paralelas no plano. Para isso, lembramos que, na aula anterior,
Capítulo 4 Distância entre duas retas. Regiões no plano Nesta aula, veremos primeiro como podemos determinar a distância entre duas retas paralelas no plano. Para isso, lembramos que, na aula anterior,
Cálculo Diferencial e Integral 2: Aproximações Lineares. Regra da Cadeia.
 Aproximações lineares. Diferenciais. Cálculo Diferencial e Integral 2: Aproximações Lineares.. Jorge M. V. Capela Instituto de Química - UNESP Araraquara, SP capela@iq.unesp.br Araraquara, SP - 2017 Aproximações
Aproximações lineares. Diferenciais. Cálculo Diferencial e Integral 2: Aproximações Lineares.. Jorge M. V. Capela Instituto de Química - UNESP Araraquara, SP capela@iq.unesp.br Araraquara, SP - 2017 Aproximações
Lista 3. Funções de Uma Variável. Derivadas III
 Lista 3 Funções de Uma Variável Derivadas III Taxas Relacionadas 5 Uma esteira transportadora está descarregando cascalho a uma taxa de 30m 3 /min formando uma pilha na forma de cone com diâmetro da base
Lista 3 Funções de Uma Variável Derivadas III Taxas Relacionadas 5 Uma esteira transportadora está descarregando cascalho a uma taxa de 30m 3 /min formando uma pilha na forma de cone com diâmetro da base
Máximos e mínimos em intervalos fechados
 Universidade de Brasília Departamento de Matemática Cálculo 1 Máximos e mínimos em intervalos fechados No texto em que aprendemos a Regra da Cadeia, fomos confrontados com o seguinte problema: a partir
Universidade de Brasília Departamento de Matemática Cálculo 1 Máximos e mínimos em intervalos fechados No texto em que aprendemos a Regra da Cadeia, fomos confrontados com o seguinte problema: a partir
x Júnior lucrou R$ 4 900,00 e que o estoque por ele comprado tinha x metros, podemos afirmar que 50
 0. O Sr. Júnior, atacadista do ramo de tecidos, resolveu vender seu estoque de um determinado tecido. O estoque tinha sido comprado ao preço de R$,00 o metro. Esse tecido foi revendido no varejo às lojas
0. O Sr. Júnior, atacadista do ramo de tecidos, resolveu vender seu estoque de um determinado tecido. O estoque tinha sido comprado ao preço de R$,00 o metro. Esse tecido foi revendido no varejo às lojas
