Exercício: Identifique e faça um esboço do conjunto solução da. 3x xy + y 2 + 2x 2 3y = 0
|
|
|
- Henrique de Almeida Bacelar
- 5 Há anos
- Visualizações:
Transcrição
1 Motivação Exercício: Identifique e faça um esboço do conjunto solução da equação 3x xy + y 2 + 2x 2 3y = 0
2 Motivação Exercício: Identifique e faça um esboço do conjunto solução da equação 3x xy + y 2 + 2x 2 3y = 0 Resposta: Este conjunto solução é a parábola obtida de y = x 2 por uma rotação de 30 o. Para resolver este problema precisamos achar os eixos pontilhados da figura que simplificam a equação.
3 Para resolver este problema precisamos achar os eixos pontilhados da figura que simplificam a equação. Eles serão localizados através de uma diagonalização. Motivação Exercício: Identifique e faça um esboço do conjunto solução da equação 3x xy + y 2 + 2x 2 3y = 0 Resposta: Este conjunto solução é a parábola obtida de y = x 2 por uma rotação de 30 o.
4 Diagonalização A teoria de diagonalização possui várias aplicações: resolução de sistemas de equações diferenciais. calcular a exponencial de uma matriz. calcular a potência de uma matriz. identificação de cônicas.
5 Diagonalização A teoria de diagonalização possui várias aplicações: resolução de sistemas de equações diferenciais. calcular a exponencial de uma matriz. calcular a potência de uma matriz. identificação de cônicas. Aulas sobre diagonalização achadas na internet. aula I. aula II.
6 Diagonalização Definição: Um matriz quadrada A é diagonalizável se existir uma matriz invertível P e se existir uma matriz diagonal D tais que P 1 AP = D
7 Diagonalização Definição: Um matriz quadrada A é diagonalizável se existir uma matriz invertível P e se existir uma matriz diagonal D tais que P 1 AP = D nem todas as matrizes são diagonalizáveis.
8 Diagonalização Definição: Um matriz quadrada A é diagonalizável se existir uma matriz invertível P e se existir uma matriz diagonal D tais que P 1 AP = D nem todas as matrizes são diagonalizáveis. vamos caracterizar as matrizes P e D em termos de A.
9 Diagonalização Definição: Um matriz quadrada A é diagonalizável se existir uma matriz invertível P e se existir uma matriz diagonal D tais que P 1 AP = D nem todas as matrizes são diagonalizáveis. vamos caracterizar as matrizes P e D em termos de A. vamos determinar condições para a existência de P invertível.
10 Diagonalização Definição: Um matriz quadrada A é diagonalizável se existir uma matriz invertível P e se existir uma matriz diagonal D tais que P 1 AP = D nem todas as matrizes são diagonalizáveis. vamos caracterizar as matrizes P e D em termos de A. vamos determinar condições para a existência de P invertível. vamos caracterizar as matrizes que são diagonalizáveis.
11 Diagonalização Definição: Um matriz quadrada A é diagonalizável se existir uma matriz invertível P e se existir uma matriz diagonal D tais que P 1 AP = D nem todas as matrizes são diagonalizáveis. vamos caracterizar as matrizes P e D em termos de A. vamos determinar condições para a existência de P invertível. vamos caracterizar as matrizes que são diagonalizáveis. depois vamos interpretar a diagonalização no contexto de cônicas no plano.
12 Diagonalização Definição: Um matriz quadrada A é diagonalizável se existir uma matriz invertível P e se existir uma matriz diagonal D tais que P 1 AP = D nem todas as matrizes são diagonalizáveis. vamos caracterizar as matrizes P e D em termos de A. vamos determinar condições para a existência de P invertível. vamos caracterizar as matrizes que são diagonalizáveis. depois vamos interpretar a diagonalização no contexto de cônicas no plano. nos cursos de Álgebra Linear 1 e 2 você pode aprender mais sobre transformações lineares A : R n R n, mudanças de bases e diagonalizações. Vale a pena.
13 Diagonalização Se uma matriz A n n é diagonalizável então existe uma matriz invertível P e existe uma matriz diagonal D tais que P 1 AP = D
14 Diagonalização Se uma matriz A n n é diagonalizável então existe uma matriz invertível P e existe uma matriz diagonal D tais que P 1 AP = D Multiplicando por P do lado esquerdo obtemos AP = PD.
15 Diagonalização Se uma matriz A n n é diagonalizável então existe uma matriz invertível P e existe uma matriz diagonal D tais que P 1 AP = D Multiplicando por P do lado esquerdo obtemos AP = PD. Fazendo um exemplo 2 2 podemos entender que se as colunas de P são X 1, X 2,..., X n e se os elementos da diagonal de D são λ 1, λ 2,..., λ n, então as colunas de AP são AX 1, AX 2,..., AX n e as colunas de PD são λ 1 X 1, λ 2 X 2,..., λ n X n.
16 Diagonalização Se uma matriz A n n é diagonalizável então existe uma matriz invertível P e existe uma matriz diagonal D tais que P 1 AP = D Multiplicando por P do lado esquerdo obtemos AP = PD. Fazendo um exemplo 2 2 podemos entender que se as colunas de P são X 1, X 2,..., X n e se os elementos da diagonal de D são λ 1, λ 2,..., λ n, então as colunas de AP são AX 1, AX 2,..., AX n e as colunas de PD são λ 1 X 1, λ 2 X 2,..., λ n X n. Como AP = PD, igualando as colunas destas duas matrizes vemos que AX 1 = λ 1 X 1, AX 2 = λ 2 X 2,..., AX n = λ n X n.
17 Diagonalização Portanto se X é uma coluna de P e se λ é o correspondente elemento da diagonal de D, provamos que X e λ estão relacionado pela equação AX = λx.
18 Diagonalização Portanto se X é uma coluna de P e se λ é o correspondente elemento da diagonal de D, provamos que X e λ estão relacionado pela equação AX = λx. Como esta equação é válida para todas as colunas, parece interessante dar uma definição para isso.
19 Diagonalização Portanto se X é uma coluna de P e se λ é o correspondente elemento da diagonal de D, provamos que X e λ estão relacionado pela equação AX = λx. Como esta equação é válida para todas as colunas, parece interessante dar uma definição para isso. Definição: Seja A uma matriz quadrada. Um número real λ é um autovalor de A se existir um vetor V 0 tal que AV = λv.
20 Diagonalização Portanto se X é uma coluna de P e se λ é o correspondente elemento da diagonal de D, provamos que X e λ estão relacionado pela equação AX = λx. Como esta equação é válida para todas as colunas, parece interessante dar uma definição para isso. Definição: Seja A uma matriz quadrada. Um número real λ é um autovalor de A se existir um vetor V 0 tal que AV = λv. Neste caso V é um autovetor associado ao autovalor λ.
21 Diagonalização Portanto se X é uma coluna de P e se λ é o correspondente elemento da diagonal de D, provamos que X e λ estão relacionado pela equação AX = λx. Como esta equação é válida para todas as colunas, parece interessante dar uma definição para isso. Definição: Seja A uma matriz quadrada. Um número real λ é um autovalor de A se existir um vetor V 0 tal que AV = λv. Neste caso V é um autovetor associado ao autovalor λ. Obs: o vetor V deve ser diferente de zero, pois estes vetores serão as colunas de P. Queremos P invertível. Logo det(p) 0. E portanto P não pode possuir uma coluna zerada.
22 Diagonalização Até o momento observamos que se A é diagonalizável com P 1 AP = D, então P é uma matriz invertível cujas colunas são autovetores, e os elementos da diagonal principal de D são os correspondentes autovalores de A.
23 Diagonalização Até o momento observamos que se A é diagonalizável com P 1 AP = D, então P é uma matriz invertível cujas colunas são autovetores, e os elementos da diagonal principal de D são os correspondentes autovalores de A. Então para achar P e D devemos calcular autovetores e autovalores.
24 Diagonalização Até o momento observamos que se A é diagonalizável com P 1 AP = D, então P é uma matriz invertível cujas colunas são autovetores, e os elementos da diagonal principal de D são os correspondentes autovalores de A. Então para achar P e D devemos calcular autovetores e autovalores. Como fazer isso?
25 Diagonalização Até o momento observamos que se A é diagonalizável com P 1 AP = D, então P é uma matriz invertível cujas colunas são autovetores, e os elementos da diagonal principal de D são os correspondentes autovalores de A. Então para achar P e D devemos calcular autovetores e autovalores. Como fazer isso? Boa pergunta, não é mesmo????
26 Autovalores e autovetores Vamos ver como podemos calcular autovalores e autovetores.
27 Autovalores e autovetores Vamos ver como podemos calcular autovalores e autovetores. Um autovetor V e o correspondente autovalor λ estão relacionados por AV = λv.
28 Autovalores e autovetores Vamos ver como podemos calcular autovalores e autovetores. Um autovetor V e o correspondente autovalor λ estão relacionados por AV = λv. Daí AV λv = 0
29 Autovalores e autovetores Vamos ver como podemos calcular autovalores e autovetores. Um autovetor V e o correspondente autovalor λ estão relacionados por AV = λv. Daí AV λv = 0 AV λi n V = 0
30 Autovalores e autovetores Vamos ver como podemos calcular autovalores e autovetores. Um autovetor V e o correspondente autovalor λ estão relacionados por AV = λv. Daí AV λv = 0 AV λi n V = 0 (A λi n )V = 0
31 Autovalores e autovetores Vamos ver como podemos calcular autovalores e autovetores. Um autovetor V e o correspondente autovalor λ estão relacionados por AV = λv. Daí AV λv = 0 AV λi n V = 0 (A λi n )V = 0 Como V não é o vetor nulo, concluímos que V é uma solução não trivial do sistema linear homogêneo (A λi n )X = 0
32 Autovalores e autovetores Um autovetor V é uma solução não nula do sistema linear homogêneo (A λi n )X = 0.
33 Autovalores e autovetores Um autovetor V é uma solução não nula do sistema linear homogêneo (A λi n )X = 0. Um sistema homogêneo possui solução não trivial quando a matriz dos coeficientes tem determinante igual a zero.
34 Autovalores e autovetores Um autovetor V é uma solução não nula do sistema linear homogêneo (A λi n )X = 0. Um sistema homogêneo possui solução não trivial quando a matriz dos coeficientes tem determinante igual a zero. Portanto para existir solução não trivial, devemos ter det(a λi n ) = 0.
35 Autovalores e autovetores Um autovetor V é uma solução não nula do sistema linear homogêneo (A λi n )X = 0. Um sistema homogêneo possui solução não trivial quando a matriz dos coeficientes tem determinante igual a zero. Portanto para existir solução não trivial, devemos ter det(a λi n ) = 0. As soluções desta equação são os autovalores λ.
36 Autovalores e autovetores Um autovetor V é uma solução não nula do sistema linear homogêneo (A λi n )X = 0. Um sistema homogêneo possui solução não trivial quando a matriz dos coeficientes tem determinante igual a zero. Portanto para existir solução não trivial, devemos ter det(a λi n ) = 0. As soluções desta equação são os autovalores λ. Então resolvemos tudo de uma vez só: já caracterizamos autovetores e autovalores!!!! Veja:
37 Autovalores e autovetores Dada uma matriz quadrada A:
38 Autovalores e autovetores Dada uma matriz quadrada A: (a) Calcule as raízes (soluções) da equação det(a λi n ) = 0. Estas raízes são os autovalores de A.
39 Autovalores e autovetores Dada uma matriz quadrada A: (a) Calcule as raízes (soluções) da equação det(a λi n ) = 0. Estas raízes são os autovalores de A. (b) Para cada λ encontrado em (a), o sistema homogêneo (A λi n )X = 0 possui solução não trivial.
40 Autovalores e autovetores Dada uma matriz quadrada A: (a) Calcule as raízes (soluções) da equação det(a λi n ) = 0. Estas raízes são os autovalores de A. (b) Para cada λ encontrado em (a), o sistema homogêneo (A λi n )X = 0 possui solução não trivial. (c) Toda solução não trivial deste sistema é um autovetor V associado ao autovalor λ.
41 Autovalores e autovetores Dada uma matriz quadrada A: (a) Calcule as raízes (soluções) da equação det(a λi n ) = 0. Estas raízes são os autovalores de A. (b) Para cada λ encontrado em (a), o sistema homogêneo (A λi n )X = 0 possui solução não trivial. (c) Toda solução não trivial deste sistema é um autovetor V associado ao autovalor λ. Observação: se V é um autovetor de A, então AV = λv. Multiplicando os dos lados desta equação por um número vemos que todo múltiplo de V também é um autovetor de A associado ao mesmo autovalor. É por este motivo que os autovetores não são únicos. E em um sistema linear homegêneo com determinante zero, sempre existem infinitas soluções.
42 Autovalores e autovetores Dada uma matriz quadrada A: (a) As raízes da equação det(a λi n ) = 0 são os autovalores.
43 Autovalores e autovetores Dada uma matriz quadrada A: (a) As raízes da equação det(a λi n ) = 0 são os autovalores. (b) Para cada autovalor λ, as solução não triviais do sistema linear homogêneo (A λi n )X = 0 são os autovetores.
44 Autovalores e autovetores Dada uma matriz quadrada A: (a) As raízes da equação det(a λi n ) = 0 são os autovalores. (b) Para cada autovalor λ, as solução não triviais do sistema linear homogêneo (A λi n )X = 0 são os autovetores. O polinômio característico de A é p(λ) = det(a λi n ).
45 Autovalores e autovetores Dada uma matriz quadrada A: (a) As raízes da equação det(a λi n ) = 0 são os autovalores. (b) Para cada autovalor λ, as solução não triviais do sistema linear homogêneo (A λi n )X = 0 são os autovetores. O polinômio característico de A é p(λ) = det(a λi n ). Os autovalores são as raízes do polinômio característico.
46 Autovalores e autovetores Exemplo 1: (a) Determine os autovalores e os autovetores da matriz [ ] 3 1 A =. 2 2 (b) Exiba uma matriz P e uma matriz diagonal D tais que AP = PD. (c) Existe uma tal matriz P invertível? Existe uma tal matriz P não invertível?
47 Autovalores e autovetores Exemplo 1: (a) Determine os autovalores e os autovetores da matriz [ ] 3 1 A =. 2 2 (b) Exiba uma matriz P e uma matriz diagonal D tais que AP = PD. (c) Existe uma tal matriz P invertível? Existe uma tal matriz P não invertível? (d) A matriz A é diagonalizável? Se for, exiba uma matriz invertível P e uma matriz diagonal D tais que P 1 AP = D.
48 Autovalores e autovetores Exemplo 2: (a) Determine os autovalores e os autovetores da matriz A = [ (b) Exiba uma matriz P e uma matriz diagonal D tais que AP = PD. (c) Existe uma tal matriz P invertível? Existe uma tal matriz P não invertível? ].
49 Autovalores e autovetores Exemplo 2: (a) Determine os autovalores e os autovetores da matriz A = [ (b) Exiba uma matriz P e uma matriz diagonal D tais que AP = PD. (c) Existe uma tal matriz P invertível? Existe uma tal matriz P não invertível? (d) A matriz A é diagonalizável? Se for, exiba uma matriz invertível P e uma matriz diagonal D tais que P 1 AP = D. ].
50 Autovalores e autovetores - diagonalização Observações importantes sobre uma dada matriz quadrada A. Sempre existe uma matriz P e sempre existe uma matriz diagonal D tais que AP = PD.
51 Autovalores e autovetores - diagonalização Observações importantes sobre uma dada matriz quadrada A. Sempre existe uma matriz P e sempre existe uma matriz diagonal D tais que AP = PD. Basta montar uma matriz P cujas colunas são autovetores e basta colocar na diagonal principal de D os correspondentes autovalores.
52 Autovalores e autovetores - diagonalização Observações importantes sobre uma dada matriz quadrada A. Sempre existe uma matriz P e sempre existe uma matriz diagonal D tais que AP = PD. Basta montar uma matriz P cujas colunas são autovetores e basta colocar na diagonal principal de D os correspondentes autovalores. De modo algum isto significa que A é diagonalizável.
53 Autovalores e autovetores - diagonalização Observações importantes sobre uma dada matriz quadrada A. Sempre existe uma matriz P e sempre existe uma matriz diagonal D tais que AP = PD. Basta montar uma matriz P cujas colunas são autovetores e basta colocar na diagonal principal de D os correspondentes autovalores. De modo algum isto significa que A é diagonalizável. Para A ser diagonalizável, precisamos achar P invertível e D diagonal tais que P 1 AP = D.
54 Autovalores e autovetores - diagonalização Observações importantes sobre uma dada matriz quadrada A. Sempre existe uma matriz P e sempre existe uma matriz diagonal D tais que AP = PD. Basta montar uma matriz P cujas colunas são autovetores e basta colocar na diagonal principal de D os correspondentes autovalores. De modo algum isto significa que A é diagonalizável. Para A ser diagonalizável, precisamos achar P invertível e D diagonal tais que P 1 AP = D. Sempre podemos passar da igualdade P 1 AP = D para a igualdade AP = PD.
55 Autovalores e autovetores - diagonalização Observações importantes sobre uma dada matriz quadrada A. Sempre existe uma matriz P e sempre existe uma matriz diagonal D tais que AP = PD. Basta montar uma matriz P cujas colunas são autovetores e basta colocar na diagonal principal de D os correspondentes autovalores. De modo algum isto significa que A é diagonalizável. Para A ser diagonalizável, precisamos achar P invertível e D diagonal tais que P 1 AP = D. Sempre podemos passar da igualdade P 1 AP = D para a igualdade AP = PD. Mas para passar da igualdade AP = PD para a igualdade P 1 AP = D a matriz P deve ser invertível.
56 Autovalores e autovetores - diagonalização Então para A n n ser diagonalizável deve ser possível montar uma matriz invertível P n n com n autovetores de A.
57 Autovalores e autovetores - diagonalização Então para A n n ser diagonalizável deve ser possível montar uma matriz invertível P n n com n autovetores de A. Lembre-se que P é invertível se det(p) 0 e que isto siginfica que as colunas de P são vetores LI.
58 Autovalores e autovetores - diagonalização Então para A n n ser diagonalizável deve ser possível montar uma matriz invertível P n n com n autovetores de A. Lembre-se que P é invertível se det(p) 0 e que isto siginfica que as colunas de P são vetores LI. Isto dá a seguinte caracterização de matrizes diagonalizáveis.
59 Autovalores e autovetores - diagonalização Então para A n n ser diagonalizável deve ser possível montar uma matriz invertível P n n com n autovetores de A. Lembre-se que P é invertível se det(p) 0 e que isto siginfica que as colunas de P são vetores LI. Isto dá a seguinte caracterização de matrizes diagonalizáveis. Teorema: uma matriz quadrada A n n é diagonalizável se A possui n autovetores LI.
60 Autovalores e autovetores - diagonalização Então para A n n ser diagonalizável deve ser possível montar uma matriz invertível P n n com n autovetores de A. Lembre-se que P é invertível se det(p) 0 e que isto siginfica que as colunas de P são vetores LI. Isto dá a seguinte caracterização de matrizes diagonalizáveis. Teorema: uma matriz quadrada A n n é diagonalizável se A possui n autovetores LI. Observe que A sempre possui n autovalores, pois os autovalores são raízes de um polinômio p(λ) = det(a λi n ) = 0 de grau n, e todo polinômio de grau n possui n raízes. Portanto a caracterização de matrizes diagonalizáveis, não pode ser dada em termos de autovalores.
61 Exemplos Verifique se cada uma das seguintes matrizes A é diagonalizável ou não. Quando for, determine uma matriz invertível P e determine uma matiz diagonal D tais que P 1 AP = D. (a) A = (b) A = (c) A = [ 7 ]
Provas. As notas da primeira e segunda prova já foram digitadas no Minha UFMG. Caso você não veja sua nota, entre em contato com o professor.
Provas As notas da primeira e segunda prova já foram digitadas no Minha UFMG. Caso você não veja sua nota, entre em contato com o professor. Terceira prova. Sábado, 15/junho, 10:00-12:00 horas, ICEx. Diagonalização
AUTOVALORES E AUTOVETORES
AUTOVALORES E AUTOVETORES Prof a Simone Aparecida Miloca Definição 1 Uma tranformação linear T : V V é chamada de operador linear. Definição Seja T : V V um operador linear. existirem vetores não-nulos
Autovalores e Autovetores Determinante de. Motivando com Geometria Definição Calculando Diagonalização Teorema Espectral:
Lema (determinante de matriz ) A B A 0 Suponha que M = ou M =, com A e D 0 D C D matrizes quadradas Então det(m) = det(a) det(d) A B Considere M =, com A, B, C e D matrizes C D quadradas De forma geral,
Matrizes Semelhantes e Matrizes Diagonalizáveis
Diagonalização Matrizes Semelhantes e Matrizes Diagonalizáveis Nosso objetivo neste capítulo é estudar aquelas transformações lineares de R n para as quais existe pelo menos uma base em que elas são representadas
Álgebra Linear I - Lista 12. Matrizes semelhantes. Diagonalização. Respostas
Álgebra Linear I - Lista 12 Matrizes semelhantes. Diagonalização Respostas 1) Determine quais das matrizes a seguir são diagonalizáveis. Nos caso afirmativos encontre uma base de autovetores e uma forma
Álgebra Linear I - Lista 11. Autovalores e autovetores. Respostas. 1) Calcule os autovalores e autovetores das matrizes abaixo.
Álgebra Linear I - Lista 11 Autovalores e autovetores Respostas 1 Calcule os autovalores e autovetores das matrizes abaixo. (a ( 4 1 1, (b ( 1 1, (c ( 5 6 3 4, (d 1 1 3 1 6 6, (e 3 5 1, (f 1 1 1 1 1 1
Autovetor e Autovalor de um Operador Linear
Autovetor e Autovalor de um Operador Linear Definição Seja T : V V um operador linear. Um vetor v V, v 0, é dito um autovetor de T se existe um número real λ tal que T (v) = λv. O número real λ acima é
3 a Avaliação Parcial - Álgebra Linear
3 a Avaliação Parcial - Álgebra Linear - 016.1 1. Considere a função T : R 3 R 3 dada por T(x, y, z) = (x y z, x y + z, x y z) e as bases de R 3 B = (1, 1, 1), (1, 0, 1), ( 1,, 0)} (a) Encontre [T] B B.
Aula 1 Autovetores e Autovalores de Matrizes Aula 2 Autovetores e Autovalores de Matrizes Casos Especiais 17
Sumário Aula 1 Autovetores e Autovalores de Matrizes.......... 8 Aula 2 Autovetores e Autovalores de Matrizes Casos Especiais 17 Aula 3 Polinômio Característico................. 25 Aula 4 Cálculo de Autovalores
GAAL - Terceira Prova - 15/junho/2013. Questão 1: Analise se a afirmação abaixo é falsa ou verdadeira:
GAAL - Terceira Prova - /junho/3 SOLUÇÕES Questão : Analise se a afirmação abaio é falsa ou verdadeira: [ A matriz A é diagonalizável SOLUÇÃO: Sabemos que uma matriz n n é diagonalizável se ela possuir
1 Autovetor e Autovalor 9. 2 Matrizes Ortogonais e Transformações Lineares Planas e Espaciais 55
Capítulo LINE LINE Autovetor e Autovalor 9 Matrizes Ortogonais e Transformações Lineares Planas e Espaciais 55 Matrizes Simétricas, o Teorema Espectral e Operadores Auto-adjuntos 8 4 Formas Bilineares,
G3 de Álgebra Linear I
G3 de Álgebra Linear I 11.1 Gabarito 1) Seja A : R 3 R 3 uma transformação linear cuja matriz na base canônica é 4 [A] = 4. 4 (a) Determine todos os autovalores de A. (b) Determine, se possível, uma forma
CM005 Álgebra Linear Lista 3
CM005 Álgebra Linear Lista 3 Alberto Ramos Seja T : V V uma transformação linear. Se temos que T v = λv, v 0, para λ K. Dizemos que λ é um autovalor de T e v autovetor de T associado a λ. Observe que λ
Álgebra Linear. Determinantes, Valores e Vectores Próprios. Jorge Orestes Cerdeira Instituto Superior de Agronomia
Álgebra Linear Determinantes, Valores e Vectores Próprios Jorge Orestes Cerdeira Instituto Superior de Agronomia - 200 - ISA/UTL Álgebra Linear 200/ 2 Conteúdo Determinantes 5 2 Valores e vectores próprios
Álgebra Linear I - Aula Forma diagonal de uma matriz diagonalizável
Álgebra Linear I - Aula 18 1 Forma diagonal de uma matriz diagonalizável 2 Matrizes ortogonais Roteiro 1 Forma diagonal de uma matriz diagonalizável Sejam A uma transformação linear diagonalizável, β =
Álgebra Linear I - Aula 20
Álgebra Linear I - Aula 20 1 Matrizes diagonalizáveis Exemplos 2 Forma diagonal de uma matriz diagonalizável 1 Matrizes diagonalizáveis Exemplos Lembramos que matriz quadrada a 1,1 a 1,2 a 1,n a 2,1 a
. Repare que ao multiplicar os vetores (-1,1) e
Álgebra Linear II P1-2014.2 Obs: Todas as alternativas corretas são as representadas pela letra A. 1 AUTOVETORES/ AUTOVALORES Essa questão poderia ser resolvida por um sistema bem chatinho. Mas, faz mais
MAT-27 Lista-09 Outubro/2011
MAT-27 Lista-09 Outubro/2011 1. Determinar, se possível, uma matriz M M 2 (R) de maneira que M 1 AM seja diagonal nos seguintes casos: [ ] 2 4 (a) 3 13 [ ] 3 2 2 1 2. Achar uma matriz diagonal semelhante
UNIVERSIDADE FEDERAL DE MINAS GERAIS (UFMG) ADÉLIO DANIEL DE SOUSA FREITAS
UNIVERSIDADE FEDERAL DE MINAS GERAIS (UFMG) ADÉLIO DANIEL DE SOUSA FREITAS O ESTUDO DA DIAGONALIZAÇÃO DE MATRIZES SIMETRICAS DE 2º ORDEM. BELO HORIZONTE 2012 ADÉLIO DANIEL DE SOUSA FREITAS O ESTUDO DA
Álgebra Linear I - Aula 22
Álgebra Linear I - Aula 1. Bases Ortonormais.. Matrizes Ortogonais. 3. Exemplos. 1 Bases Ortonormais Lembre que uma base β é ortogonal se está formada por vetores ortogonais entre si: para todo par de
MAT2458 ÁLGEBRA LINEAR PARA ENGENHARIA II 2 a Prova - 2 o semestre de T ( p(x) ) = p(x + 1) p(x), (a) 8, (b) 5, (c) 0, (d) 3, (e) 4.
MAT2458 ÁLGEBRA LINEAR PARA ENGENHARIA II 2 a Prova - 2 o semestre de 218 Q1. Considere a transformação linear T : P 3 (R) P 2 (R), dada por T ( p(x) ) = p(x + 1) p(x), para todo p(x) P 3 (R), e seja A
Segunda prova de Álgebra Linear - 01/07/2011 Prof. - Juliana Coelho
Segunda prova de Álgebra Linear - 01/07/011 Prof - Juliana Coelho JUSTIFIQUE SUAS RESPOSTAS! Questões contendo só a resposta, sem desenvolvimento ou justificativa serão desconsideradas! QUESTÃO 1, pts
Parte 3 - Produto Interno e Diagonalização
Parte 3 - Produto Interno e Diagonalização Produto Escalar: Sejam u = (u 1,..., u n ) e v = (v 1,..., v n ) dois vetores no R n. O produto escalar, ou produto interno euclidiano, entre esses vetores é
G3 de Álgebra Linear I
G3 de Álgebra Linear I 2.2 Gabarito ) Considere a matriz 4 N = 4. 4 Observe que os vetores (,, ) e (,, ) são dois autovetores de N. a) Determine uma forma diagonal D de N. b) Determine uma matriz P tal
Resolução das objetivas 3ª Prova de Álgebra Linear II da UFRJ, período
www.engenhariafacil.weebly.com Resolução das objetivas 3ª Prova de Álgebra Linear II da UFRJ, período 4. OBS: Todas as alternativas corretas são as letras A. ) Devemos utilizar o teorema que diz: (Im(A
Autovalores e Autovetores
Autovalores e Autovetores Maria Luísa B. de Oliveira SME0300 Cálculo Numérico 24 de novembro de 2010 Introdução Objetivo: Dada matriz A, n n, determinar todos os vetores v que sejam paralelos a Av. Introdução
APLICAÇÃO DE AUTOVALORES E AUTOVETORES NAS POTÊNCIAS DE MATRIZES
Universidade Federal de Goiás Câmpus de Catalão Departamento de Matemática Seminário Semanal de Álgebra APLICAÇÃO DE AUTOVALORES E AUTOVETORES NAS POTÊNCIAS DE MATRIZES Aluno: Ana Nívia Pantoja Daniela
Capítulo 4 - Valores e Vectores Próprios
Capítulo 4 - Valores e Vectores Próprios Carlos Balsa balsa@ipb.pt Departamento de Matemática Escola Superior de Tecnologia e Gestão de Bragança Matemática I - 1 o Semestre 2011/2012 Matemática I 1/ 17
Álgebra Linear I - Aula 19
Álgebra Linear I - Aula 19 1. Matrizes diagonalizáveis. 2. Matrizes diagonalizáveis. Exemplos. 3. Forma diagonal de uma matriz diagonalizável. 1 Matrizes diagonalizáveis Uma matriz quadrada T = a 1,1 a
Análise multivariada
UNIFAL-MG, campus Varginha 11 de Setembro de 2018 Dada uma matriz A (p p), podemos obter um escalar λ e um vetor v (p 1) de modo que seja satisfeita? Av = λv (1) Dada uma matriz A (p p), podemos obter
Álgebra Linear (MAT-27) Ronaldo Rodrigues Pelá. 21 de outubro de 2011
APLICAÇÕES DA DIAGONALIZAÇÃO Álgebra Linear (MAT-27) Ronaldo Rodrigues Pelá IEFF-ITA 21 de outubro de 2011 Roteiro 1 2 3 Roteiro 1 2 3 Introdução Considere a equação de uma cônica: Forma Geral Ax 2 + Bxy
ficha 4 valores próprios e vectores próprios
Exercícios de Álgebra Linear ficha 4 valores próprios e vectores próprios Exercícios coligidos por Jorge Almeida e Lina Oliveira Departamento de Matemática, Instituto Superior Técnico 2 o semestre 2011/12
GAAL Exercícios 6: Umas soluções
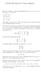GAAL Exercícios 6: Umas soluções. Quais dos seguintes vetores são combinação linear de u = (5, 3, ), v = (, 4, 3), w = (, 8, 7)? (a) (, 2, 5) (b) (, 2, 8) (c) ( 2, ) (d) (, 2, 3). O conjunto {u, v, w}
P3 de Álgebra Linear I
P3 de Álgebra Linear I 2008.2 Data: 14 de Novembro de 2008. Gabarito. 1) Decida se cada afirmação a seguir é verdadeira ou falsa. Considere uma transformação linear T : R 3 R 3 tal que existem vetores
Equação Geral do Segundo Grau em R 2
8 Equação Geral do Segundo Grau em R Sumário 8.1 Introdução....................... 8. Autovalores e autovetores de uma matriz real 8.3 Rotação dos Eixos Coordenados........... 5 8.4 Formas Quadráticas..................
Polinômio Mínimo e Operadores Nilpotentes
Capítulo 9 Polinômio Mínimo e Operadores Nilpotentes Curso: Licenciatura em Matemática Professor-autor: Danilo Felizardo Barboza Wilberclay Gonçalves Melo Disciplina: Álgebra Linear II Unidade II Aula
Algebra Linear. 1. Revisitando autovalores e autovetores. 2. Forma Diagonal e Forma de Jordan. 2.1 Autovalores distintos. 2.2 Autovalores complexos
Algebra Linear 1. Revisitando autovalores e autovetores 2. Forma Diagonal e Forma de Jordan 2.1 Autovalores distintos 2.2 Autovalores complexos 2.3 Nem todos autovalores distintos 3. Autovalores e autovetores
Universidade Federal de Viçosa Centro de Ciências Exatas e Tecnológicas Departamento de Matemática
1 Universidade Federal de Viçosa Centro de Ciências Exatas e Tecnológicas Departamento de Matemática Lista 4 - MAT 137 -Introdução à Álgebra Linear 2017/II 1. Entre as funções dadas abaixo, verifique quais
Capítulo 5. Operadores Auto-adjuntos. Curso: Licenciatura em Matemática. Professor-autor: Danilo Felizardo Barboza Wilberclay Gonçalves Melo
Capítulo 5 Operadores Auto-adjuntos Curso: Licenciatura em Matemática Professor-autor: Danilo Felizardo Barboza Wilberclay Gonçalves Melo Disciplina: Álgebra Linear II Unidade II Aula 5: Operadores Auto-adjuntos
1 Diagonalização de Matrizes 2 2. Sistemas de Equações Diferenciais Lineares
Diagonalização de Matrizes e Sistemas de Equações Diferenciais Lineares Reginaldo J Santos Departamento de Matemática-ICE Universidade Federal de Minas Gerais http://wwwmatufmgbr/~regi 3 de setembro de
Álgebra Linear I - Aula 21
Álgebra Linear I - Aula 1 1. Matrizes ortogonalmente diagonalizáveis: exemplos. Matrizes simétricas. Roteiro 1 Matrizes ortogonalmente diagonalizáveis: exemplos Exemplo 1. Considere a matriz M = 4 4 4
Módulos. Volume 2ª edição. Hernando Bedoya Ricardo Camelier. Álgebra Linear II
Módulos 1e2 Volume 2ª edição Hernando Bedoya Ricardo Camelier Álgebra Linear II 1 Álgebra Linear II Volume 1 - Módulos 1 e 2 2ª edição Hernando Bedoya Ricardo Camelier Apoio: Fundação Cecierj / Consórcio
Álgebra Linear I - Aula Autovetores e autovalores de uma transformação
Álgebra Linear I - Aula 18 1. Autovalores e autovetores. 2. Cálculo dos autovetores e autovalores. Polinômio característico. Roteiro 1 Autovetores e autovalores de uma transformação linear Considere uma
Álgebra Linear e Geometria Analítica. Valores Próprios e Vectores Próprios
Álgebra Linear e Geometria nalítica Valores Próprios e Vectores Próprios Será assim para todos os vectores? R α α, Será assim para todos os vectores? Definição: Seja um número real e uma matriz quadrada
Forma Canônica de Matrizes 2 2
Forma Canônica de Matrizes Slvie Olison Kamphorst Departamento de Matemática - ICE - UFMG Versão. - Novembro 5 a b Seja A c d induzida por A uma matriz real e seja T a transformação operador linear de
GAAL - Exame Especial - 12/julho/2013. Questão 1: Considere os pontos A = (1, 2, 3), B = (2, 3, 1), C = (3, 1, 2) e D = (2, 2, 1).
GAAL - Exame Especial - /julho/3 SOLUÇÕES Questão : Considere os pontos A = (,, 3), B = (, 3, ), C = (3,, ) e D = (,, ) (a) Chame de α o plano que passa pelos pontos A, B e C e de β o plano que passa pelos
Álgebra Linear I - Aula 18
Álgebra Linear I - Aula 18 1. Matrizes semelhantes. 2. Matriz de uma transformação linear em uma base. Roteiro 1 Matrizes semelhantes Definição 1 (Matrizes semelhantes). Considere duas matrizes quadradas
Diagonalização de Operadores. Teorema Autovetores associados a autovalores distintos de um operador linear T : V V são linearmente independentes.
Teorema Autovetores associados a autovalores distintos de um operador linear T : V V são linearmente independentes. Teorema Autovetores associados a autovalores distintos de um operador linear T : V V
5 a Lista de Exercícios de Introdução à Álgebra Linear IMPA - Verão Encontre os autovalores, os autovetores e a exponencial e At para
5 a Lista de Exercícios de Introdução à Álgebra Linear IMPA - Verão 2008 1. Encontre os autovalores, os autovetores e a exponencial e At para [ ] 1 1 1 1 2. Uma matriz diagonal Λ satisfaz a regra usual
Geovan Tavares, Hélio Lopes e Sinésio Pesco PUC-Rio Departamento de Matemática Laboratório Matmidia
Álgebra Linear Computacional Geovan Tavares, Hélio Lopes e Sinésio Pesco PUC-Rio Departamento de Matemática Laboratório Matmidia http://www.matmidia.mat.puc-rio.br 1 Álgebra Linear Computacional - Parte
ÁLGEBRA LINEAR - MAT0024
UNIVERSIDADE FEDERAL DA INTEGRAÇÃO LATINO-AMERICANA Instituto Latino-Americano de Ciências da Vida e Da Natureza Centro Interdisciplinar de Ciências da Natureza ÁLGEBRA LINEAR - MAT0024 11 a Lista de exercícios
Resolução das objetivas 3ª Prova de Álgebra Linear II da UFRJ, período
www.engenhariafacil.weebly.com Resolução das objetivas 3ª Prova de Álgebra Linear II da UFRJ, período 2013.2 OBS: Todas as alternativas corretas são as letras A. 1) Para encontrar o autovetor associado
Exponencial de uma matriz
Exponencial de uma matriz Ulysses Sodré Londrina-PR, 21 de Agosto de 2001; Arquivo: expa.tex Conteúdo 1 Introdução à exponencial de uma matriz 2 2 Polinômio característico, autovalores e autovetores 2
ÁLGEBRA LINEAR I - MAT0032
UNIVERSIDADE FEDERAL DA INTEGRAÇÃO LATINO-AMERICANA Instituto Latino-Americano de Ciências da Vida e Da Natureza Centro Interdisciplinar de Ciências da Natureza ÁLGEBRA LINEAR I - MAT0032 11 a Lista de
Álgebra Linear Diagonalização de Operadores
Introdução e Motivação Preliminares Diagonalização de Operadores Aplicações Referências Álgebra Linear Diagonalização de Operadores Universidade Estadual Vale do Acaraci - Sobral - CE Semana da Matemática
Valores e vectores próprios
ALGA - Eng Civil e EngTopográ ca - ISE - / - Valores e vectores próprios 5 Valores e vectores próprios Neste capítulo, sempre que não haja especi cação em contrário, todas as matrizes envolvidas são quadradas
Álgebra Linear I - Lista 10. Matrizes e Transformações lineares. Respostas
Álgebra Linear I - Lista 1 Matrizes e Transformações lineares Respostas 1 Sejam A e B matrizes quadradas do mesmo tamanho Dê um exemplo onde (A + B 2 A 2 + 2A B + B 2 Complete: (A + B 2 = A 2 + B 2 +?
CM005 Álgebra Linear Lista 2
CM005 Álgebra Linear Lista 2 Alberto Ramos 1. Seja M M n (R) uma matriz. Mostre que se {v 1,..., v p } R n é linearmente dependente, então {Mv 1,..., Mv p } é também linearmente dependente. Agora suponha
Álgebra Linear e suas Aplicações Notas de Aula. Petronio Pulino = Q
Álgebra Linear e suas Aplicações Notas de Aula Petronio Pulino 1 3 4 3 1 0 4 0 1 = Q 4 1 6 Qt Q t Q = 1 1 1 PULINUS Álgebra Linear e suas Aplicações Notas de Aula Petronio Pulino Departamento de Matemática
(c) apenas as afirmações (II) e (III) são necessariamente verdadeiras;
Q1. Considere o espaço vetorial R 4 munido do seu produto interno usual. Sejam B uma base de R 4, A M 4 (R) uma matriz e T : R 4 R 4 a transformação linear tal que [T ] B = A. Considere as seguintes afirmações:
Teorema da Triangularização de Schur e Diagonalização de Matrizes Normais
Teorema da Triangularização de Schur e Diagonalização de Matrizes Normais Reginaldo J Santos Departamento de Matemática-ICEx Universidade Federal de Minas Gerais http://wwwmatufmgbr/~regi 16 de novembro
(d) p(λ) = λ(λ + 1) (b) 4 (c) 1 (d) Seja A uma matriz n n. Assinale a alternativa FALSA:
UFRJ Instituto de Matemática Disciplina: Algebra Linear II - MAE 125 Professor: Bruno Costa, Luiz Carlos Guimarães, Mário de Oliveira, Milton Ramirez, Monique Carmona, Nilson Bernardes e Nilson Roberty
Legenda. Questões. Lista de Exercícios - Autovalores e autovetores. Cálculos Teoria Geometria
Lista de Exercícios - Autovalores e autovetores Legenda Cálculos Teoria Geometria Questões. Considere o quadrado determinado pelos pontos A(0, 0), B(, 0), C(, ) e D(0, ).Em cada item aplique o referido
Universidade Federal Fluminense - GAN
Solimá Gomes Pimentel Universidade Federal Fluminense IM - GAN Solimá Gomes Pimentel, ****- Matemática para Economia III/Solimá Gomes Pimentel 2pt, ; 31cm Inclui Bibliografia. 1. Matemática para Economia
Geometria anaĺıtica e álgebra linear
Geometria anaĺıtica e álgebra linear Francisco Dutenhefner Departamento de Matematica ICEx UFMG 22/08/13 1 / 24 Determinante: teorema principal Teorema: Se A é uma matriz quadrada, então o sistema linear
Parte I. Álgebra Linear. Sistemas Dinâmicos Lineares. Autovalores, autovetores. Autovalores, autovetores. Autovalores e Autovetores.
Sistemas Dinâmicos Lineares Romeu Reginatto Programa de Pós-Graduação em Engenharia de Sistemas Dinâmicos e Energéticos Universidade Estadual do Oeste do Paraná Parte I Álgebra Linear Adaptado das notas
Álgebra Linear I - Aula Matrizes simultaneamente ortogonais e simétricas
Álgebra Linear I - Aula 22 1. Matrizes 2 2 ortogonais e simétricas. 2. Projeções ortogonais. 3. Matrizes ortogonais e simétricas 3 3. Roteiro 1 Matrizes simultaneamente ortogonais e simétricas 2 2 Propriedade
Álgebra Linear I - Aula Propriedades dos autovetores e autovalores
Álgebra Linear I - Aula 17 1. Propriedades dos autovetores e autovalores. 2. Matrizes semelhantes. 1 Propriedades dos autovetores e autovalores Propriedade 1: Sejam λ e β autovalores diferentes de T e
Álgebra Matricial Notas de Aulas 3 ( Terceira Avaliação ) Prof Carlos Alberto S Soares
Álgebra Matricial Notas de Aulas 3 ( Terceira Avaliação Prof Carlos Alberto S Soares 1 Matrizes Diagonais Lembramos que uma matriz A n n será dita matriz diagonal de ordem n se todos os elementos fora
Instituto Superior Técnico Departamento de Matemática Última actualização: 3/Dez/2003 ÁLGEBRA LINEAR A
Instituto uperior Técnico Departamento de Matemática ecção de Álgebra e Análise Última actualização: 3/Dez/2003 ÁLGEBRA LINEAR A REVIÃO DA PARTE IV Parte IV - Diagonalização Conceitos: valor próprio, vector
P4 de Álgebra Linear I de junho de 2005 Gabarito
P4 de Álgebra Linear I 25.1 15 de junho de 25 Gabarito 1) Considere os pontos A = (1,, 1), B = (2, 2, 4), e C = (1, 2, 3). (1.a) Determine o ponto médio M do segmento AB. (1.b) Determine a equação cartesiana
1. Entre as funções dadas abaixo, verifique quais são transformações lineares: x y z
MINISTÉRIO DA EDUCAÇÃO E DO DESPORTO UNIVERSIDADE FEDERAL DE VIÇOSA 657- - VIÇOSA - MG BRASIL a LISTA DE EXERCÍCIOS DE MAT 8 I SEMESTRE DE Entre as funções dadas abaixo, verifique quais são transformações
FORMA CANÔNICA DE JORDAN
FORMA CANÔNICA DE JORDAN Álgebra Linear (MAT-27) Ronaldo Rodrigues Pelá IEFF-ITA 4 de novembro de 2011 Roteiro Motivação 1 Motivação 2 3 4 5 6 Roteiro Motivação 1 Motivação 2 3 4 5 6 Matrizes Quase Diagonalizáveis
3 a Lista de Exercícios de Introdução à Álgebra Linear IMPA - Verão e B =
3 a Lista de Exercícios de Introdução à Álgebra Linear IMPA - Verão 2008. (a) Ache os auto-valores e auto-vetores de A = 3 4 2 0 2 0 0 0 e B = 0 0 2 0 2 0 2 0 0 (b) Mostre que λ + λ 2 + λ 3 é igual ao
CSE-020 Revisão de Métodos Matemáticos para Engenharia
CSE-020 Revisão de Métodos Matemáticos para Engenharia Engenharia e Tecnologia Espaciais ETE Engenharia e Gerenciamento de Sistemas Espaciais L.F.Perondi Engenharia e Tecnologia Espaciais ETE Engenharia
G3 de Álgebra Linear I
G de Álgebra Linear I 7 Gabarito ) Considere a transformação linear T : R R cuja matriz na base canônica E = {(,, ), (,, ), (,, )} é [T] E = a) Determine os autovalores de T e seus autovetores correspondentes
Aula 5 - Produto Vetorial
Aula 5 - Produto Vetorial Antes de iniciar o conceito de produto vetorial, precisamos recordar como se calculam os determinantes. Mas o que é um Determinante? Determinante é uma função matricial que associa
ÁLGEBRA LINEAR. Valores Próprios (Autovalores) e Vetores Próprios (Autovetores) Prof. Susie C. Keller
ÁLGEBRA LINEAR Valores Próprios (Autovalores) e Vetores Próprios (Autovetores) Prof. Susie C. Keller Autovalores e Autovetores de um Operador Linear Seja T:V V um operador linear. Um vetor v V, v 0, é
Roteiros e Exercícios - Álgebra Linear v1.0
Roteiros e Exercícios - Álgebra Linear v1.0 Robinson Alves Lemos 14 de janeiro de 2017 Introdução Este material é um roteiro/apoio para o curso de álgebra linear da engenharia civil na UNEMAT de Tangará
Marcelo M. Santos DM-IMECC-UNICAMP msantos/
Universidade Estadual de Maringá - Departamento de Matemática Cálculo Diferencial e Integral: um KIT de Sobrevivência 0 anos c Publicação Eletrônica do KIT http://www.dma.uem.br/kit Identificação de Cônicas
Álgebra Linear I - Aula Matriz de uma transformação linear em uma base. Exemplo e motivação
Álgebra Linear I - Aula 19 1. Matriz de uma transformação linear em uma base. Exemplo e motivação 2. Matriz de uma transformação linear T na base β 1 Matriz de uma transformação linear em uma base. Exemplo
Aula 19 Operadores ortogonais
Operadores ortogonais MÓDULO 3 AULA 19 Aula 19 Operadores ortogonais Objetivos Compreender o conceito e as propriedades apresentadas sobre operadores ortogonais. Aplicar os conceitos apresentados em exemplos
TÓPICOS. Valores e vectores próprios. Equação característica. Matrizes semelhantes. Matriz diagonalizável. Factorização PDP -1
Note bem: a leitura destes apontamentos não dispensa de modo algum a leitura atenta da bibliografia principal da cadeira Chama-se a atenção para a importância do trabalho pessoal a realizar pelo aluno
Valores e vectores próprios
Valores e vectores próprios Álgebra Linear C (Engenharia Biológica) 0 de Dezembro de 006 Conteúdo Motivação e definições Propriedades 4 3 Matrizes diagonalizáveis 5 Motivação e definições Considere a matriz
(d) v é um autovetor de T se, e somente se, T 2 = T ; (e) v é um autovetor de T se, e somente se, T (v) = v.
Q1. Seja V um espaço vetorial real de dimensão finita munido de um produto interno. Sejam T : V V um operador linear simétrico e W um subespaço de V tal que T (w) W, para todo w W. Suponha que W V e que
Primeira prova de Álgebra Linear - 06/05/2011 Prof. - Juliana Coelho
Primeira prova de Álgebra Linear - 6/5/211 Prof. - Juliana Coelho JUSTIFIQUE SUAS RESPOSTAS! Questões contendo só a resposta, sem desenvolvimento ou justificativa serão desconsideradas! QUESTÃO 1 (2, pts)
Unidade 22 - Teorema espectral para operadores simétricos, reconhecimento de cônicas. A. Hefez e C. S. Fernandez Resumo elaborado por Paulo Sousa
MA33 - Introdução à Álgebra Linear Unidade 22 - Teorema espectral para operadores simétricos, reconhecimento de cônicas A. Hefez e C. S. Fernandez Resumo elaborado por Paulo Sousa PROFMAT - SBM 10 de agosto
SME Gustavo C. Buscaglia
SME0602-2017 Gustavo C. Buscaglia ICMC - Ramal 738176, gustavo.buscaglia@gmail.com Cálculo de autovalores e autovetores Existem vários problemas na engenharia em que precisamos calcular os autovalores
7 temos que e u =
Capítulo 1 Complementos de Álgebra Linear 11 Introdução Seja A = [a ij ] uma matriz quadrada de ordem n e pensemos na transformação linear R n! R n que a cada cada vector u R n faz corresponder um vector
5. Seja R : R 3 R 3 uma rotação em torno do eixo gerado por (0, 0, 1). Suponha que R mande o vetor
Universidade Federal do Rio de Janeiro Instituto de Matemática Disciplina: Álgebra Linear II Professor: Bruno Costa, Cesar Niche, Francesco Noseda, Luiz Carlos Guimarães, Mário de Oliveira, Milton Ramirez,
(I) T tem pelo menos um autovalor real; (II) T é diagonalizável; (III) no espaço vetorial real R n, o conjunto {u, v} é linearmente independente.
Q1. Sejam n um inteiro positivo, T : C n C n um operador linear e seja A = [T ] can a matriz que representa T em relação à base canônica do espaço vetorial complexo C n. Suponha que a matriz A tenha entradas
Dou Mó Valor aos Autovalores
1. Definições Preliminares Dou Mó Valor aos Autovalores 21ª Semana Olímpica Maceió, AL Prof. Davi Lopes Nível U Dada uma matriz quadrada A n n de entradas complexas, podemos definir os conceitos a seguir,
Recados. Listas 1 e 2 - disponíveis no site. Procurar Monitoria GAAL 2013/1 UFMG no Facebook. Primeira Prova: sábado, 06 de abril
Recados Listas 1 e 2 - disponíveis no site Procurar Monitoria GAAL 2013/1 UFMG no Facebook Primeira Prova: sábado, 06 de abril Horário: 10:00-12:00 no ICEx Da aula anterior: Da aula anterior: Teorema:
MAE125 Álgebra Linear /1 Turmas EQN/QIN
MAE25 Álgebra Linear 2 205/ Turmas EQN/QIN Planejamento (última revisão: 0 de junho de 205) Os exercícios correspondentes a cada aula serão cobrados oralmente na semana seguinte à aula e valem nota Todas
Álgebra Linear /2 Turma EM1 (unificada)
Álgebra Linear 2 2013/2 Turma EM1 (unificada) Planejamento preliminar (última revisão: 3/4/2013) Os exercícios correspondentes a cada aula serão discutidos na aula seguinte e não valem nota Este planejamento
Algoritmos Numéricos 2 a edição
Algoritmos Numéricos 2 a edição Capítulo 2: Sistemas lineares c 2009 FFCf 2 2.1 Conceitos fundamentais 2.2 Sistemas triangulares 2.3 Eliminação de Gauss 2.4 Decomposição LU Capítulo 2: Sistemas lineares
G4 de Álgebra Linear I
G4 de Álgebra Linear I 20122 Gabarito 7 de Dezembro de 2012 1 Considere a transformação linear T : R 3 R 3 definida por: T ( v = ( v (1, 1, 2 (0, 1, 1 a Determine a matriz [T ] ε da transformação linear
. (1) Se S é o espaço vetorial gerado pelos vetores 1 e,0,1
QUESTÕES ANPEC ÁLGEBRA LINEAR QUESTÃO 0 Assinale V (verdadeiro) ou F (falso): (0) Os vetores (,, ) (,,) e (, 0,) formam uma base de,, o espaço vetorial gerado por,, e,, passa pela origem na direção de,,